数形结合 “说”出精彩

蒋世雷 郑闽

［摘  要］ 在分数乘除法解决问题的教学中，教师应借助几何直观、数形结合等方法，让学生深刻理解分数和分数乘法的意义，加强基本数量关系和各类解决问题的算理及算法的口述训练，沟通与其他相关知识的联系，帮助学生厘清并拓展解决问题的思路。

［关键词］ 分数乘除法；解决问题；几何直观；数形结合；口述训练

与整数、小数的解决问题相比，分数乘除法解决问题由于数量关系比较抽象，学生理解难度增大，因此一直是解决问题教学中的一个难点。怎样突破这一教学难点呢？笔者认为，教师应整体把握分数乘除法解决问题的教学内容，关注教学内容自身的结构化，处理好教学内容的整体性、一致性和阶段性等关系，紧扣分数的意义和分数乘法的意义，借助实物图、直条图、线段图等几何直观手段，让学生建立形与数的联系，构建数学问题的直观模型，并利用图表分析实际情境与数学问题，探索出各类解决问题的思路。

分数乘除法解决问题的教学，从纵的方面来说，要提前训练，多层次孕伏；从横的方面来说，一要充分揭示分数乘除法解决问题本身各要素之间的关系，加强基本数量关系的训练，二要溝通与此有关的其他知识（如倍数、比等）的联系。在教学中，教师应如何利用几何直观来加强学生解决问题分析思路的口述训练呢？

一、借助直观，深度理解

在分数乘除法解决问题的教学中，教师应整体把握教学内容，厘清层次，提前规划训练，步步孕伏铺垫，运用几何直观手段、数形结合等方法，从分率句（即用分数反映两个量之间的关系句）入手，引导学生紧扣分数的意义理解分率句所反映的两个量的倍比关系，在理解的基础上厘清数量关系，探寻解题思路，为形成算法渐次过渡。

1.结合分数的意义用份数理解分率句，提前孕伏

到了五年级下期，学生开始系统地认识分数的意义，对分数的认识更加抽象。学生真正理解分数，特别是对分率句的理解，这需要一个长期渐进的过程。

（1）包含关系分率句的理解。

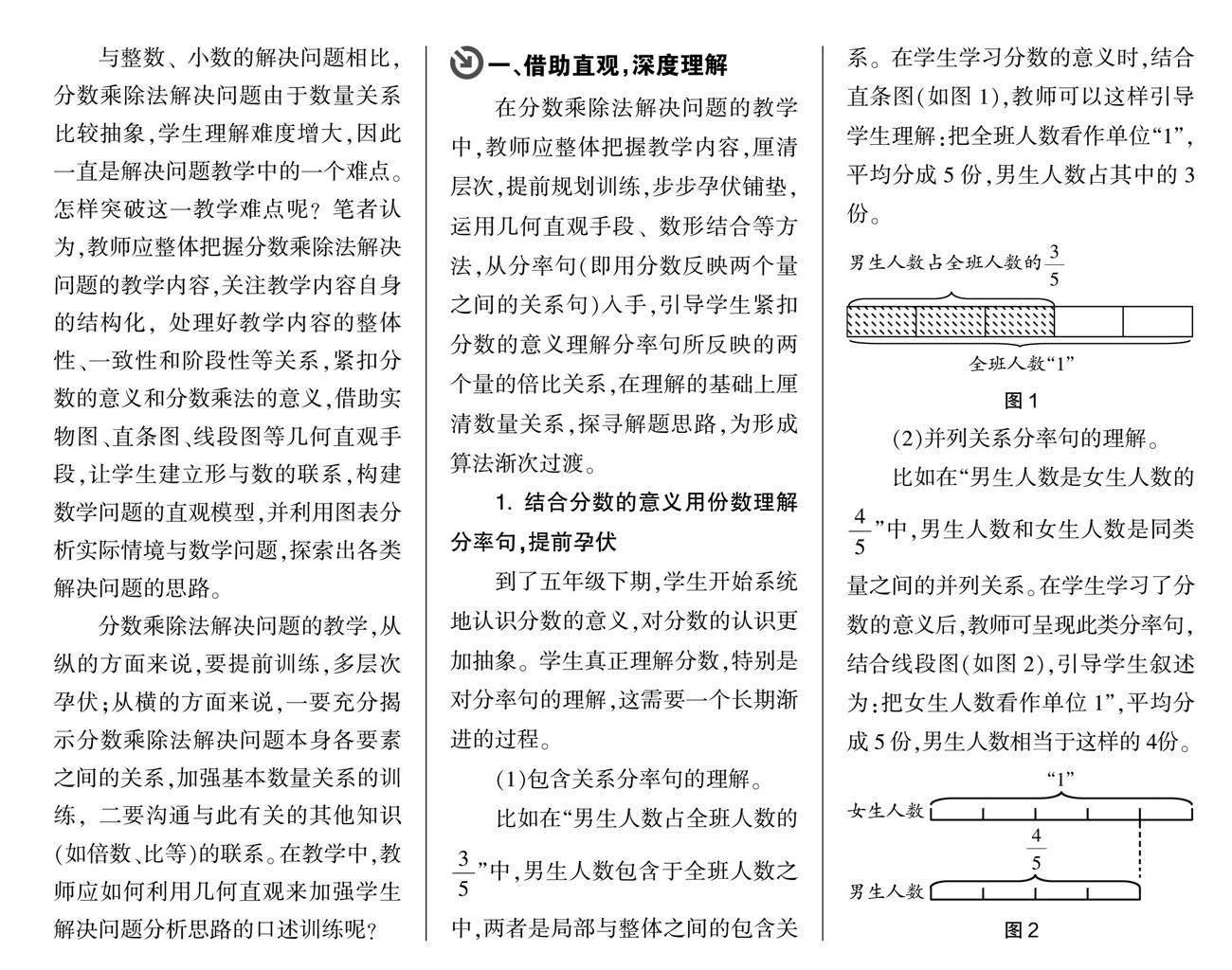
比如在“男生人数占全班人数的”中，男生人数包含于全班人数之中，两者是局部与整体之间的包含关系。在学生学习分数的意义时，结合直条图（如图1），教师可以这样引导学生理解：把全班人数看作单位“1”，平均分成5份，男生人数占其中的3份。

（2）并列关系分率句的理解。

比如在“男生人数是女生人数的”中，男生人数和女生人数是同类量之间的并列关系。在学生学习了分数的意义后，教师可呈现此类分率句，结合线段图（如图2），引导学生叙述为：把女生人数看作单位1”，平均分成5份，男生人数相当于这样的4份。

此类口述训练，既加深了学生对分数意义的理解，又沟通了分数与份数的联系，同时为用份数来解决与分数乘除法相关的问题做了提前孕伏，可谓“一石三鸟”。叙述时教师可以用课件逐步呈现直条图或线段图，帮助学生更好地用份数来理解。

2. 分数乘法计算教学中透彻理解一个数乘分数的实际意义

在六年级的分数乘法的计算教学中，教师要让学生知道：分数乘整数的意义和整数乘法的意义相同，都是求几个相同加数的和，即求几个几是多少；一个数乘分数的意义，就是求一个数的几分之几是多少。前者体现出整数、小数、分数乘法意义的一致性，学生容易理解，教学时教师应重点关注后者。在分数乘法的计算教学中，教师应如何通过数形结合提前孕伏，帮助学生理解透一个数乘分数的意义呢？

比如，教师可以出示以下练习：

（1）你能画图分别表示出8个苹果、12个苹果的吗？

（2）8个苹果的是几个苹果？12个苹果的是几个苹果？说一说你是怎么想的？

（3）都是这些苹果的，为什么苹果的个数不一样？

在第（2）个问题中，教师可以引导学生这样叙述理解：8个苹果的是把8个苹果看作单位“1”，平均分成4份，每份是8÷4=2（个），其中的3份就是2×3=6（个）苹果，所以8个苹果的是6个苹果。同样，12个苹果的是把12个苹果看作单位“1”，平均分成4份，每份是12÷4=3（个），其中的3份就是3×3=9（个）苹果，所以12个苹果的是9个苹果。通过这样的口述训练，学生弄清了求一个数的，根据分数的意义，就是把这个数平均分成4份，取其中的3份是多少，由此帮助学生建立起分数的意义与求一个数的几分之几的内在联系（如图3）。

在上面的练习中，教师通过数形结合恰当地处理了直观与抽象的关系，引导学生通过对数学内容的直观表述既理解了的意义，还理解了由于单位“1”不同，同样是单位“1”的，但是所表示具体数量并不相同。这样的练习沟通了一个数乘分数的实际意义与分数的意义之间的联系，为以后的分数乘法中用“求一个数的几分之几是多少”来解决问题做好了铺垫。

3. 强化“求一个数的几分之几是多少”解决问题中解题思路的口述训练

学生透彻理解了一个数乘分数的意义后，教师即可在分数乘法的解决问题教学中强化“求一个数的几分之几是多少”解题思路的口述训练。众所周知，在分数乘除法的解决问题教学中，简单的用分数乘法解决问题是基础。因此，在分数乘法的计算教学中，教师要充分结合分数乘法的意义，在具体的问题情景中借助线段图或直观图让学生充分感知并理解一个数乘分数的意义，就是求这个数的几分之几是多少。

（1）简单的“求一个数的几分之几是多少”？

西南大学版教材六年级上册分数乘法例题：从甲地到乙地共有84千米，已经行了全程的，汽车已经行了多少千米？

教师先引导学生画出线段图（如图4），然后引导学生结合线段图从分率句入手，用份数和一个数乘分数的意义分析解题的思路。

①用份数分析：“行了全程的”，把全程看作单位“1”，平均分成3份，行了的路程占其中的2份。已知全程是84千米，平均分成3份，每份是84÷3=28（千米），2份是28×2=56（千米）。列式为：84÷3×2=56（千米）。

②用一个数乘分数的意义分析：“行了全程的”是指已经行了的路程占全程的，把全程看作单位“1”，已经行了的路程=全程×，已知全程是84千米，求已經行了多少千米，就是求84千米的是多少，用乘法算，列式为：84×=56（千米）。

（2）稍复杂的“求一个数的几分之几是多少”？

如前所述，在用分数乘除法解决问题中，简单的用分数乘法解决问题是基础和关键。如果学生掌握了用分数乘法解决问题的解题思路，在面对稍复杂的用分数乘除法解决问题时，也能从基本的数量关系和基本的解法迁移拓展过去。

比如在教学“足球有20个，篮球的个数比足球多，篮球有多少个”时，教师先引导学生理解题意，画出线段图（如图5），然后结合线段图，从分率句入手用不同的思路进行分析。

分析一：“篮球的个数比足球多”，是把足球的个数看作单位“1”，篮球的个数相当于足球个数的1+，已知足球有20个，求篮球有多少个，就是求20个的1+是多少，列式为：20×1+=25（个）。

分析二：“篮球的个数比足球多”，是把足球的个数看作单位“1”，篮球比足球多的个数相当于足球个数的。已知足球有20个，所以篮球比足球多20×=5（个），再用20+5=25（个）即可求出篮球的个数。

二、数形结合，注重归类

“结构化”是数学的学科特点，数学教学的内容、方法都具有高度的结构化特征。因此，在教学过程中，教师要站在整体、系统和结构的高度把握、处理教学内容，从数学知识结构和学生认知结构出发设计与组织教学。在分数乘除法解决问题的教学中，教师要帮助学生借助实物图或线段图等直观图示，厘清各种基本类型的结构，在各种类型的解决问题教学中加强口述训练，帮助学生弄清分析问题的思路，从而提升学生分析问题、解决问题的能力。

比如，在“求一个数是另一个数的几分之几是多少”类型的题目解题思路口述训练时，以解决问题“合唱队有男生15人，女生20人，男生人数是女生人数的几分之几”为例，教师应紧扣分数的意义，引导学生这样分析：求“男生人数是女生人数的几分之几”，是把“男生人数”同“女生人数”做比较，因此“女生人数”是标准，是单位“1”。题目中“男生有15人，女生有20人”，根据分数的意义，可以这样想：把“女生人数”看作单位“1”，平均分成20份，男生有这样的15份，所以男生人数是女生人数的，列式为：15÷20=。

大部分教材都将“求一个数是另一个数的几分之几”的教学安排在“分数的意义”教学之后，此时学生还没有学习约分等知识。如果学生学习了约分以后，教师可以引导学生将5个人作为1份，画出实物图（如图6）或线段图（如图7），然后采用数形结合的方法引导学生分析：如果把5个人作为1份，求男生人数是女生人数的几分之几，是把女生人数看作单位“1”，平均分成20÷5=4份，男生有这样的15÷5=3份，所以男生人数是女生人数的。列式为：15÷20==。

三、运用图表，沟通关联

1. 厘清乘除法的关联性，根据乘除法的互逆关系完善基本数量关系和解决思路的口述训练

在学生理解了“一个数乘分数，就是求这个数的几分之几”这一含义后，笔者要求学生先读分率句，找出单位“1”，然后说出基本的数量关系。比如在“男生人数是女生人数的”中，笔者引导学生这样理解：“把女生人数看作单位‘1，男生人数＝女生人数×。”在充分理解算理的基础上，学生根据乘除法的互逆关系得出“女生人数＝男生人数÷”后，还可以开展这一数量关系的口述训练（如表1）。这样学生对基本的用分数乘除法解决问题的算理理解更深刻，算法形成更清晰，更易于知识的系统化。

如前所述，在用分数乘除法解决问题中，简单的用分数乘法解决问题是基础和关键。如果学生掌握了用分数乘法解决问题的解题思路，在教学“已知一个数的几分之几是多少，求这个数”时，学生自然而然就会想到用方程解或根据乘除法的互逆关系来解答。在解答稍复杂的用分数乘除法解答的解决问题时，学生也能从基本的数量关系和基本的解法迁移拓展过去。

2. 联想训练

实践证明，在教学用分数乘除法来解决问题的教学中，“多想几步”这种训练方法，对打开学生思路和提高解题能力很有帮助。比如“一段路，已修了全长的”，要求学生想到“还剩全长的”；“一堆煤，第一次运走这堆煤的，第二次运走这堆煤的”，要求学生想到“两次共运走这堆煤的”“第二次比第一次多运走这堆煤的”“还剩下这堆煤的1－－＝”（见表2）。

“多想”是根据整体与部分之间的内在联系、部分与部分之间的内在联系来实现的。经过“多想几步”训练，可以使题目中隐含的数量明朗化，开阔学生的解题思路，提高学生的解题能力。

3. 沟通与其他知识的联系

在分数乘除法解决问题的教学中，教师要适度引导学生结合所学的其他知识进行沟通训练，实现知识上的融会贯通。比如在比的相关知识教学后，教师应重点引导学生找出整体与部分之间、部分与部分之间存在的各种倍比关系，并将相关的两个量之间的比和分率关系之间的相互转化清晰地表述出来，把分数、份数、倍数、比等相关知识联系起来。比如，对于“苹果树的棵数比梨树多”，教师可以引领学生从不同角度理解和口述（如表3）。

在此基础上，教师还可以通过设计题组来沟通用分数乘除法解决问题和用份数、倍数、比的知识等来解决问题之间的联系，以形成更宏大的知识体系。这为学生掌握、拓展并优化解决问题的策略提供了坚实的基础，进一步培养学生的学习能力、实践能力和创新能力。

总之，几何直观有助于学生把握问题的本质和明晰思维的路径。在分数乘除法解决问题的教学中，教师应从整体把握好教学内容，利用实物图、条形图、线段图等几何直观、数形结合等方法，提前孕伏，层层深入，让学生深刻理解分数和分数乘除法的意义，注重各种类型解决问题思路的口述训练，利用图表沟通与其他相关知识的联系，探索出解决问题的多种思路，从而达到理想的教学效果。