模糊结合代数的商及同态定理

杨晓曼,周 鑫,2

(1.伊犁师范大学数学与统计学院,新疆 伊宁 835000;2.伊犁师范大学应用数学研究所,新疆 伊宁 835000)

0 引言

1965年,ZADEH[1]引入了模糊集的概念,标志着模糊数学的诞生.1986年,NANDA[2]给出了模糊域以及模糊线性空间的定义.1989年,BISWAS[3]重新给出了由NANDA定义的模糊域以及模糊线性空间,这种定义更为合理.1990至1991年,NANDA[4]讨论了模糊域上的模糊代数的概念,并给出了模糊理想的概念.NANDA[5]进一步引入了任意值域上的模糊线性空间中的一些概念,如凸模糊集等.1993年,GU等[6]指出NANDA对模糊域的定义是不合理的,因此模糊域上模糊代数的定义也是不合理的;且重新定义了模糊域和模糊代数;在没有任何限制的情况下,证明了模糊代数的同态像是模糊代数.1996年,党发宁[7]更深入地探讨了模糊代数以及模糊理想的性质,定义了模糊商代数,并证明了代数Y关于代数Z的同态核f-1[Oz]的模糊商代数与代数Z同构等性质.2002年,孙绍权等[8]定义了模糊商代数,给出了模糊代数的同态基本定理.同年,姚炳学等[9]重新定义了模糊域上的模糊商代数,研究了模糊域上的模糊代数与模糊理想的性质,并给出了模糊商代数的同构定理.2019年,魏晓伟等[10]引入了模糊集上模糊泛代数的概念,研究了商代数、同余关系等概念.2021年,ADDIS[11]引入了L-值模糊代数的概念,并讨论了模糊陪集的结构.

本文基于以上模糊代数的研究内容,首先,给出了模糊结合代数的概念,在此基础上定义了模糊结合代数之间的模糊同态、模糊单同态、模糊满同态以及模糊同构.其次,证明了模糊同态的复合仍然是模糊同态.然后,引出了模糊结合代数中模糊理想的概念,利用模糊理想构造了模糊结合代数的商结构.最后,在上述定义的基础上证明了模糊结合代数的同态定理.

1 预备知识

定义1[12]设(L,≤)为偏序集,若任意a,b∈L,均存在最小上界sup{a,b}和最大下界inf{a,b},则称偏序集(L,≤)为格,简记为L.

在L中定义∨和∧两种运算,对于任意a,b∈L,a∨b=sup{a,b},a∧b=inf{a,b}.若格L的每一个子集S均有最小上界和最大下界,则称L为完备格.

定义2[13]设X是一个非空集合,L为完备格,映射χ:X→L称为集合X的模糊子集,其中χ称为模糊子集的隶属函数.对于任意x∈X,χ(x)称为x对χ的隶属度.用FL(X)={χ|χ:X→L}表示X上所有隶属函数的族.

2 主要结论

本文中代数均指具有单位元e的结合代数.

定义3 设A是数域F上的一个代数,L为完备格.若χA∈FL(A),任意a1,a2∈A,k∈F,满足:

(1)χA(a1)∧χA(a2)≤χA(a1+a2),

(2)χA(a1)∧χA(a2)≤χA(a1·a2),

(3)χA(a1)≤χA(k·a1),

(4)χA(e)=1.

则称χA是A上的模糊结合代数,简称模糊代数,记为(A,χA).

定义4 设(A,χA),(B,χB)为模糊代数,α:A→B为A到B的同态.若任意a∈A,满足:

χA(a)≤χB(α(a)),

则称映射α:(A,χA)→(B,χB)为(A,χA)到(B,χB)的模糊同态.

若模糊同态α为单射,则称α:(A,χA)→(B,χB)为(A,χA)到(B,χB)的模糊单同态.

若模糊同态α为满射,则称α:(A,χA)→(B,χB)为(A,χA)到(B,χB)的模糊满同态.

若模糊同态α为双射,则称α:(A,χA)→(B,χB)为(A,χA)到(B,χB)的模糊同构.

注1 (1)任意a∈A,若α:(A,χA)→(B,χB)为模糊同态,则χB(α(a))=∨χA(α-1(α(a))).

(2)任意a∈A,若α:(A,χA)→(B,χB)为模糊同构,则χB(α(a))=χA(a).

定理1设(A,χA),(B,χB),(C,χC)为模糊代数,α:(A,χA)→(B,χB)为(A,χA)到(B,χB)的模糊同态,β:(B,χB)→(C,χC)为(B,χB)到(C,χC)的模糊同态,则复合β∘α:(A,χA)→(C,χC)为(A,χA)到(C,χC)的模糊同态.

证明 设a∈A,α(a)=b,β(b)=c,则(β∘α)(a)=c.

由模糊同态的定义可知,χA(a)≤χB(α(a)),χB(b)≤χC(β(b)),则有:

χA(a)≤χB(α(a))=χB(b)≤χC(β(b))=χC(c)=χC((β∘α)(a)),

即χA(a)≤χC((β∘α)(a)),故复合β∘α为(A,χA)到(C,χC)的模糊同态.

定义5 设(A,χA),(B,χB)为模糊代数,α,β为(A,χA)到(B,χB)的模糊同态.若任意a∈A,α(a)=β(a)均成立,则称模糊同态α与β相等,记为α=β.

定义6 设A是代数,R为A的子代数,L为完备格,χR∶R→L.

(1)若a∈A,b∈R,有χR(a·b)≥χR(b),则称(R,χR)是(A,χA)的模糊左理想;

(2)若a∈R,b∈A,有χR(a·b)≥χR(a),则称(R,χR)是(A,χA)的模糊右理想;

(3)若a,b∈R,有χR(a·b)≥χR(a)∨χR(b),则称(R,χR)是(A,χA)的模糊理想.

定义7 设(A,χA)为模糊代数,(R,χR)是(A,χA)的模糊理想.任意a,b∈A,k∈F,在A/R上可以定义运算:

(1)加法:(a·R)+(b·R)=(a+b)·R;

(2)乘法:(a·R)·(b·R)=(a·b)·R;

(3)数乘:k(a·R)=(ka)·R.

定理2设(A,χA)为模糊代数且存在a∈A,使得χA(a)=1,(R,χR)是(A,χA)的模糊理想,定义:

则(A/R,χA/R)为模糊代数,称(A/R,χA/R)为(A,χA)的模糊商代数.

证明 先验证乘法运算下结论是否成立.

(1)假设a1,a2∈R,则

χA/R((a1·R)·(a2·R))=χA/R((a1·a2)·R)=1,

故χA/R(a1·R)∧χA/R(a2·R)≤χA/R((a1·R)·(a2·R)).

(2)假设a1∈R,a2∉R,则

由于χA/R(a1·R)=1,则

χA/R(a1·R)∧χA/R(a2·R)=χA/R(a2·R),

故χA/R(a1·R)∧χA/R(a2·R)≤χA/R((a1·R)·(a2·R)).

因此,在乘法运算下结论成立.加法运算、数乘运算的证明同理可得,且χA/R(e)=1.

综上所述,(A/R,χA/R)为模糊代数.

定理3设(A,χA)为模糊代数且存在a∈A,使得χA(a)=1,(R,χR)是(A,χA)的模糊理想,(A/R,χA/R)为(A,χA)的模糊商代数.对于任意a′∈A,定义映射:

ν∶(A,χA)→(A/R,χA/R),ν(a′)=a′·R,

则ν为模糊同态.

证明 先验证乘法运算下结论是否成立.

(1)假设a1,a2∈R,则

χA/R((a1·R)·(a2·R))=χA/R((a1·a2)·R)=1,

故χA(a1)∧χA(a2)≤χA/R((a1·R)·(a2·R)).

(2)假设a1∈R,a2∉R,则

即χA(a1)∧χA(a2)≤χA/R((a1·R)·(a2·R)).

因此,在乘法运算下结论成立.加法运算、数乘运算的证明同理可得,零元运算的结论显然成立.

综上所述,ν为模糊同态.

定理4设(A,χA)为模糊代数且存在a∈A,使得χA(a)=1,α是(A,χA)到(B,χB)的模糊满同态,(R,χR)是(A,χA)的模糊理想,(A/R,χA/R)为(A,χA)的模糊商代数.其中,

当a′∈R时,χB(α(a′))=1.ν:(A,χA)→(A/R,χA/R)为模糊同态,且对于任意a′∈A,有ν(a′)=a′·R,则存在唯一的模糊同态:

β∶(A/R,χA/R)→(B,χB),

使得图1交换.

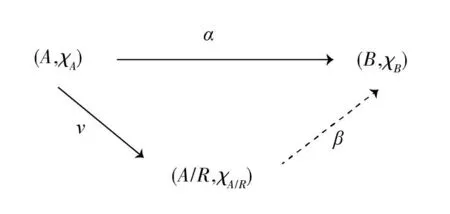
图1 交换图

证明 (i)存在性.对于任意a′∈A,令映射β:(A/R,χA/R)→(B,χB),β(a′·R)=α(a′),则β是A/R到B的同态,且β∘ν(a′)=β(a′·R)=α(a′),即β∘ν=α.

下证χA/R((a1·a2)·R)≤χB(β((a1·a2)·R)).

先验证乘法运算下结论是否成立.

(1)假设a1,a2∈R,则

χB(β((a1·a2)·R))=χB(α(a1·a2))=1=χA/R((a1·a2)·R).

(2)假设a1∈R,a2∉R,则

任意a1,a2∈A,因为

χB(α(a1·a2))=∨χA(α-1(α(a1·a2)))≥χA(a1)∧χA(a2),

故

χA/R((a1·a2)·R)≤χB(β((a1·a2)·R)).

因此,在乘法运算下结论成立.加法运算、数乘运算的证明同理可得,零元运算的结论显然成立.

(ii)唯一性.假设存在同态β′:A/R→B同样满足上述条件,即对于任意a′∈A,有β′∘ν(a′)=α(a′),可推出对于任意a′∈A,有β′∘ν(a′)=β∘ν(a′)均成立,又由于ν为满同态,则可推出β′=β.由经典交换图(图2)中β的唯一性可知,交换图(图1)中的β唯一存在.

图2 经典交换图

3 结语

本文主要研究了模糊结合代数的理想以及商等相关性质,证明了模糊结合代数的同态定理.文中的定理、结论有助于更好地理解其他具体的模糊代数结构,并且为研究其他模糊代数结构提供了理论支撑.