广义的WBKL方程和HS-KdV方程的微分不变量、微分不变方程

雷桂英,宋军锋

(陕西师范大学数学与统计学院,陕西 西安 710119)

0 引言

微分不变量是非线性系统的重要应用方面,也是不变量经典理论的组成部分,而不变量是抽象代数的一部分.微分不变量用于求解不变微分方程和变分问题[1-2],确定其显示解和守恒律的基本构件.子流形的等价性、对称性[3]和刚性都由它们的微分不变量决定.此外,微分不变量在微分几何和相对论、偏微分方程组特解的构造[4-5]、计算机视觉中的物体识别[6]、可积系统、几何数值积分[7]、经典不变量理论、不变流以及许多其他纯数学和应用数学领域[8-12]中的应用比比皆是.

考虑广义的Whitham-Broer-Kaup-Like(WBKL)方程组[13]:

其中,u(x,t)和v(x,t)表示待定函数,a,b,c为任意常数.

该方程组可用于描述长波在浅水波中的双向传播,这是一个非常重要的物理模型.该系统包含许多大家熟知的非线性演化方程,当参数取不同值时,该方程组可导出许多著名的非线性演化方程.广义的WBKL方程组已被许多学者以各种方法进行了深入研究. GUO等[14]应用推广的(G′/G)展开法,得到了WBKL方程的具有双曲函数、三角函数、有理函数形式的行波解.MING等[15]利用分歧方法和动力系统定性理论得到了WBKL方程的扭结解、爆破解、周期爆破解和孤立波解.LI等[16]应用简化了的齐次平衡法,借助线性方程组解的非线性变换得到了WBKL方程的许多精确解.

考虑广义的Hirota-Satsuma耦合KdV方程[17]:

此方程是Hirota-Satsuma耦合KdV方程的可积推广.许多学者已经对广义的HS-KdV方程进行了大量研究.ENGUI[18]应用扩展的tanh函数法获得了方程新的孤子解.YU等[19]使用推广的Jacobi椭圆函数法得到了方程更一般的解,该通解不但包含了已有的Jacobi椭圆函数展开法求得的解,还包含了许多新的显式解.YONG等[20]使用改进的投影Riccati方程法得到了方程的许多精确解.

本文以广义的WBKL方程组和广义的HS-KdV方程组为研究对象,运用最新的等变活动标架理论[21-24],选择合适的群轨道横截面,并对其进行规范化以获得活动标架,进而产生基本的微分不变量,再利用Gröbner基算法计算微分不变量代数的基本结构,借助符号计算软件Maple,切实有效地求得广义的WBKL方程和广义的Hirota-Satsuma耦合KdV方程的微分不变量、微分不变量代数和微分不变方程．

1 基础知识

下面给出等变活动标架理论和微分不变量的相关定义和定理.

给定微分方程组:

Δv(x,u(n))=0,

(3)

其中,x=(x1,…,xp)表示p个自变量,u=(u1,…,uq)表示q个因变量.z=(x,u)是全空间M上的局部坐标,M是m=p+q维的流形,SΔ={Δ(x,u(n))=0}⊂Jn(M,p)是全空间M上p维子流形的n阶Jet丛的子簇.

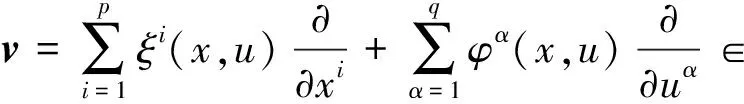
n阶延拓向量场为:

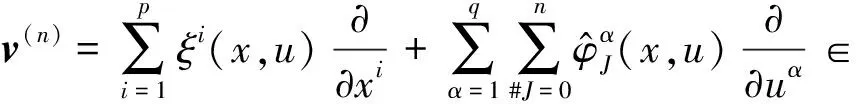
其中,DJ=Dxj1,…,Dxjk,J=(j1,…,jk),1≤jv≤p表示相应的迭代全微分,延拓系数为:

v(n)(Δv)=0,v=1,2,…,k.(4)

在SΔ上展开(4)式,关于向量场v的系数ξi和φα满足的齐次线性偏微分方程组:

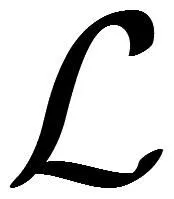
系统的提升水平余标架如下:

(6)

其中,dH表示水平微分,Dj=Dxj表示全微分.

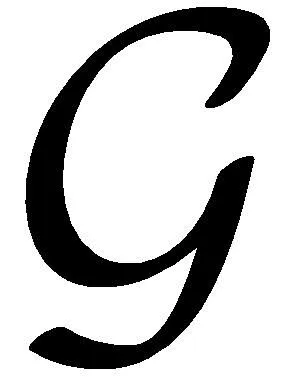
一旦一个活动标架被固定,可诱导出不变量化过程ι,将Jn(M,p)上的微分函数、微分形式、微分算子映射到微分不变量、不变微分形式、不变微分算子.不变量是通过用它们的活动标架归一化来替换变换对象中的群参数.因此,不变量化过程为:

ι:F(x,u(n))I(x,u(n))=F(ρ(n)(x,u(n))·(x,u(n))).

将微分函数F(x,u(n))映射到微分不变量I=ι(F).从几何角度来讲,不变量化是把函数限制在横截面上,并且要求其沿着伪群轨道是恒定的.因此,ι定义了一个代数态射,将微分函数的代数投影到微分不变量的代数上.特别地,由活动标架诱导的正规化微分不变量是通过对n阶Jet坐标(x,u(n))不变量化得到的.

(7)

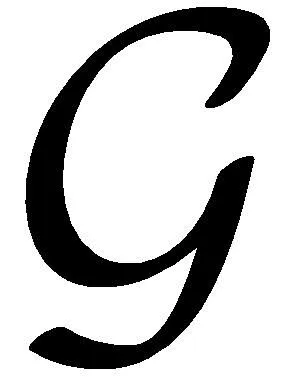
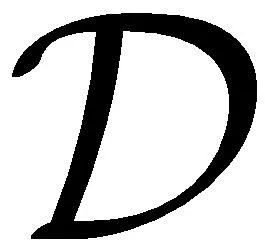
xiXi,uα

定理3不变性的Maurer-Cartan形式满足不变性的决定方程:

定理4正规化微分不变量(7)之间的递推公式为:

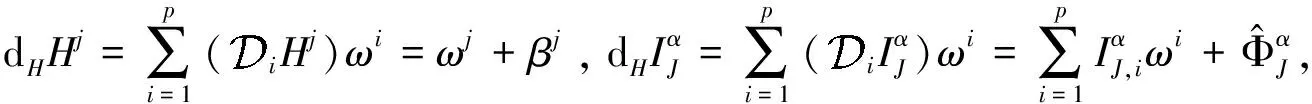
2 广义的Whitham-Broer-Kaup-Like(WBKL)方程组

运用最新的等变活动标架理论计算方程组(1)的微分不变量、微分不变量代数以及微分不变方程.

方程组(1)的全空间M=4的坐标为(t,x,u,v),其向量场为:

方程组(1)对应的无穷小决定方程可约化为:

上述方程组的通解为:

(8)

定义四维广义的WBKL方程的对称代数,其基为:

通过指数映射,得到对应的李伪群:

其中,λ1,λ2,λ3,λ4是群参数.

根据(6)式可得方程组(1)的水平余标架:

dHT=(Tt+Tuut+Tvvt)dt+(Tx+Tuux+Tvvx)dx=eλ4dt,

(9)

(10)

和对偶的隐式全微分算子:

(11)

构造广义的WBKL方程的活动标架,选取群轨道的坐标截面,得到四个归一化方程:

X=0,T=0,U=0,V=1.

解得群参数:

λ1=-t,λ2=-x,λ3=-u,λ4=lnv.

(13)

将(13)式代入(12)式,得到幻影微分不变量:

和函数独立的正规化微分不变量的完整系统:

将式(13)代入式(9)、(10)式,得到不变量化的水平余标架,并且不变量化的水平1-形式ω1,ω2满足结构方程:

(14)

再将式(13)代入式(11),得到不变的微分算子:

(15)

通过对偶性,由式(14)可得不变微分算子的交换关系:

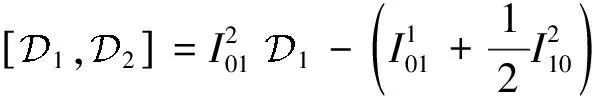
根据定理2和定理3可得不变量化的Maurer-Cartan形式满足的方程:

(16)

根据式(8),设无穷小生成子的一般形式为:

其中,c1,c2,c3,c4是常参数,延拓系数为:

(17)

对式(17)不变量化可得如下的递推公式:

根据定理4可得:

0=dHH1=ω1+α,0=dHH2=ω2+β,

(18)

由式(18)解得:

将上述结果代入式(18),再根据定理4,整理使得等式两边ω1,ω2的系数相等,得到微分不变量的递推公式:

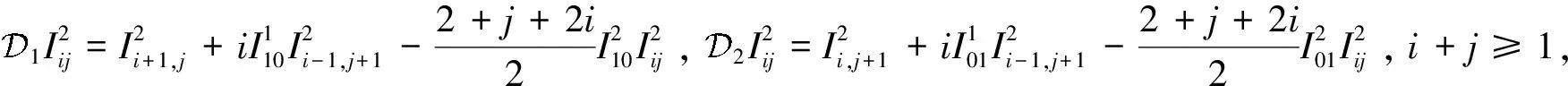
(19)

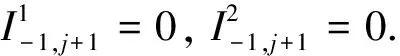
由式(19)可知,每一个正规化微分不变量都可以由这4个基本的微分不变量:

根据Gröbner基算法,由式(15)和(19)可得到广义的WBKL方程微分不变量代数的基本关系:

根据等变活动标架理论可得方程组(1)的微分不变方程为:

3 广义的Hirota-Satsuma耦合KdV方程

运用最新的等变活动标架理论计算方程组(2)的微分不变量、微分不变量代数以及微分不变方程.

方程组(2)的全空间M=5的坐标为(t,x,u,v,w),其向量场为:

方程组(2)对应的无穷小决定方程可约化为:

上述方程组的通解为:

(20)

定义四维广义的Hirota-Satsuma耦合KdV方程的对称代数,其基为:

通过指数映射,得到对应的李伪群为:

其中,λ1,λ2,λ3,λ4是群参数.

根据式(6)可得方程组(2)的水平余标架:

(21)

dHT=(Tt+Tuut+Tvvt+Twwt)dt+(Tx+Tuux+Tvvx+Twwx)dx=eλ4dt,

(22)

和对偶的隐式全微分算子:

(23)

构造广义的Hirota-Satsuma耦合KdV方程的活动标架,选取群轨道的坐标截面,得到4个归一化方程:

T=0,X=0,U=1,V=1.

解得群参数:

(25)

将式(25)代入式(24)得到幻影微分不变量:

和函数独立的正规化微分不变量的完整系统:

将式(25)代入式(21)、(22)得到不变量化的水平余标架,并且不变量化的水平1-形式ω1,ω2满足结构方程:

(26)

再将式(25)代入式(23)得到不变的微分算子:

(27)

通过对偶性,由式(26)可得不变微分算子的交换关系:

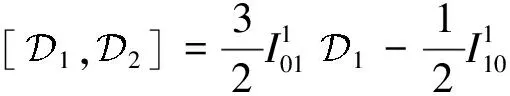
根据定理2和定理3可知,不变量化的Maurer-Cartan形式满足的方程:

(28)

根据式(20)设无穷小生成子的一般形式为:

其中,c1,c2,c3,c4是常参数,延拓系数为:

(29)

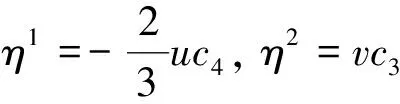
对式(29)不变量化,可得如下的递推公式:

(30)

根据定理4可得:

由式(31)解得:

将上述结果代入式(30),再根据定理4,整理使得等式两边ω1,ω2的系数相等,得到微分不变量的递推公式:

(32)

由式(32)可知,每一个正规化微分不变量都可以由6个基本的微分不变量:

根据Gröbner基算法,由式(27)和式(32)可得到广义的Hirota-Satsuma耦合KdV方程微分不变量代数的基本关系:

根据最新的等变活动标架理论可得方程组(2)的微分不变方程为:

4 结语

本文基于最新的等变活动标架理论,选取合适的伪群轨道截面,构造方程的活动标架,借助数学软件,有效求得了广义的WBKL方程组和广义的HS-KdV方程组的微分不变量、微分不变量代数以及微分不变方程.这一结果可作为利用微分不变量求解方程的不变解和有关不变量问题的重要工具.