运算教学一致性的思考与实践

王灵勇 姜滢

［摘  要］ 运算领域的知识存在一定的内在逻辑关联，教师要基于整体视角进行结构化教学，体现运算教学的一致性。通过对二年级学生进行调研，以及从教材、学生认知特点、教师的教学进行深入分析，探究学生在“退位减法”计算时易错的原因。基于新课标运算教学一致性理念，研究者提出内容从模糊到清晰、算理从表面到深入、练习从单一到系统等三个方面的对策。

［关键词］ 错误；退位减法；算理

一、问题缘起

笔者在教学二年级退位减法（被减数中间和末尾有零）时发现学生虽然做对了题，但是不明白算理。在导学环节笔者出示题目：500-348，让学生先独立开展试学，然后请“小先生”展示交流自己的计算方法。

笔者根据学生的反馈情况进行追问深研：“十位上答案5你是怎么想的？”学生A回答：“十位上的0不够减，需要从百位借出1。”这时候学生B举手回答：“我没算，但是我不明白为什么要向个位退1，所以十位就是9。”

笔者追问：“你们听懂了吗？被减数个位上的‘0、十位上的‘0上面都有退位点，怎么个位是10、十位变成9了呢？”

学生的回答让笔者陷入了沉思：0上都有退位点，为什么被减数十位上变成9呢？学生理解的难点在哪里？教师在教学中需要特别注意什么呢？

二、深入调查

退位减法的教学中，当哪一位不够减的时候向高位借“1”，在这一过程中学生运算时常常会出现一些问题。上述课堂教学中学生不明白算理是个别现象，还是普遍现象呢？基于此，笔者对学校三年级4个班160名学生进行了一次调研（测试内容如下）。

1. 列竖式计算

（1）500-298=  （2）350-149=

（3）409-314=  （4）114-107=

（5）135-46=   （6）203-193=

（7）814-737=  （8）423-269=

（9）100-591=  （10）6375-486=

（11）403-158= （12）1010-999=

2. 选择题

（1）在计算500-298时，按照怎样的顺序点退位点（   ）。

A． 先点十位，再点百位

B． 先点百位，再点十位

C． 没有规定

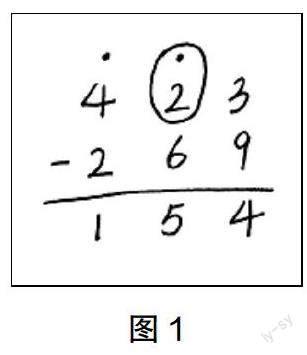
（2）如图1，所表示的竖式计算中，圈出部分所代表的含义是多少？

A． 2   B． 1   C． 12   D． 11

（3）如图2，所表示的竖式计算中，圈出部分所代表的含义是什么？

A． 10-1  B． 9+1  C． 没有含义

总体而言，学生对退位运算的理解有难度，错误率很高。其中列竖式计算（具体情况统计如表1）中题（7）、题（9）连续退位学生错误率分别是35.86%和28.97%；题（1）第一步先确定退位点在哪个位置的错误率有14.48%；题（8）退位点表示实际含义学生错误率有24.14%；题（11）被减数数中间有0，需要向高位借“1”错误率很高，达到了37.93%。

退位有两种不同的意义，第一种表示向前一位借“1”；第二种表示和原来的数相加。学生在计算过程中忘记和原来的数字相加，类似的错误占30%以上。学生受到知识经验的影响，不能理解退位的意义：有时候要求退位一次却退位了两次（如图3），有时候根本没有退位却退位（图4），有时候不需要退位却退位（图5），忘记加原来的数字（图6），1和0退位后含义混淆（图7），忘记连续退位（图8）。

三、成因分析

调研测试中的第一种题是立足于教材内容进行灵活变换，而第二种题是根据退位点的理解改编的。笔者通过对错例的分析和对学生进行访谈，发现学生退位减法中存在诸多的问题。

1. 思维过程的单一

低年级的学生数学思维比较单一，学生对退位减法算理的理解比较薄弱。学生需要经历复杂的思维过程才能理解什么时候进行退位运算、怎样进行退位运算。比如在教学三位数连续退位减法时，多个数位连续进行退位形成了错综复杂的思维过程，这是教学的一大难点。特别是十位、百位、千位上相减时，既要从高位上“退1当10”，与本数位上的数字相加再减，同时还要减去借走的1后继续减，但是低年级的学生思维缺少全局性，导致错误频出。

2. 繁与简的矛盾

解决退位减法问题蕴含着很多的方法策略和结构化思维路径，比如前测中学生呈现的问题：该退位1次的时候，却进行了2次退位；百位和千位退位遗忘，不该退位的时候乱退位；借来1以后忘记和原数相加，连续数位出现退位错误频繁；数位上1和0的退位运算难以区分等。在实际的教学过程中，教师为了提高学生计算技能和速度，常常让学生在实际的计算过程中省去繁杂的计算过程，以实现计算简便，达到计算方法自动化水平。

3. 教学中的不足

（1）教学过程过急

运算教学中部分教师为追求正确率和速度，忽视了学生对运算过程的探究，想当然地认为运算课比较简单，并忽视了学生学习过程的持续推进，对算理的探究教得过急，过早总结运算的方法，用自己的“教”取代了学生的“学”，导致学生对算理悟得不深、学得不透。事实上，学生对连续退位过程意义的理解是比较难的，教师要借助几何直观充分展示交流学生的竖式计算过程，激活语言表征，帮助学生理解退位减法算理的本质。

（2）退位意识淡薄

為什么会出现退位减法？数学源于生活，退位减法的产生源于现实生活的需要。比如计算72-45，教材会提供退位减法的过程暗示，个位上2不够减6，这时需要到十位上借1，表示1个10，12减5等于7。在实际的教学过程中，教师要鼓励学生采用不同的方法进行计算和对比沟通，体现算理的一致性。比如，有的学生会把72看作75，75减45，得30，再减3得27；有的学生先看十位，先用70减40，再用32减5得27等。教师要让学生在方法对比辨析中发现不管哪种方法都有退位的过程，其“理”具有一致性，将退位意识根植在学生的头脑中。

（3）错因分析不透彻

学生退位减法出错时，教师往往简单粗暴地解决，认为是学生审题不认真，计算不认真，过于粗心，打个叉叉，让学生继续订正，或者通过反复的练习加强巩固。但是在后续的作业中学生仍然频繁出错，这样的教学治标不治本。事实上很多的错误并非学生粗心所致，而是由于学生计算能力的不足，计算素养的缺失，对计算方法领悟不透。

四、教學对策

数学课程标准强调课程内容要体现整体性，要体现运算教学的一致性。教师要打通运算及运算之间内在关联性，体现运算教学的一致性，提高学生的运算能力和推理意识。运算教学一致性不仅体现在教学内容之间存在一致性，也体现在知识背后的思想与方法存在一致性，即所谓的“通法”［１］。

1. 内容展示：由模糊到清晰

培养学生计算技能，教师要让学生深刻理解每一步运算的道理，要通过问题导学、自主试学、展学交流、研学分析、类比，实现不同方法之间的融会贯通，对算法的理解从混沌变清晰。

（1）算式和图的类比

案例1  百以内的退位减法

活动1：学生根据具体情境（如图9），尝试列式解答。

活动2：直观辅助理解算理。

你能看懂小棒图（如图9）表示的意思吗？它和算式之间有怎样的联系？说一说自己的想法。

活动3：根据图列出减法算式。

师：如图10，看到图形，你能想到什么算式？

生：314-25。

师：该得几呢？……

（2）竖式间的沟通

教师要读懂学生的思维，沟通学生不同的算法，纠正学生错误的想法，计算教学才能实现“明理通法”。课堂上，当学生出现很多的计算方法后，教师要选择典型方法，引导学生对比分析两组算式之间的区别和联系。

对比一：如图11，两种方法计算顺序不同，左边先十位后个位，右边先个位后十位。

对比二：如图12，两种计算过程不同，左边先加后减，右边先减后加。

对比三：如图13，左右两边退位计算的记作方式不同。

学生的思维方式是百花齐放的，在教学中稍纵即逝，课堂上教师要充分利用这些有价值的学生作品开展深度探究，达到“明理通法”，融会贯通。上述案例中，有的学生受口算方法的影响采取了先算高位再算低位；有的学生受巧算方法的影响采用了先减后加；还有的学生对退位进行了个性化的理解。通过不同层次的对比分析，学生明晰了低位算起计算“序”的重要性，规范了退位运算的过程。

2. 算理理解：由表面到本质

教学是一门“慢艺术”，教师要让学生充分经历探究算法、理解算理的过程，激活学生已有知识经验，通过数形结合、动手操作、类比迁移、总结归纳等方法理解算理本质。

（1）图示——显现算理

在被减数末尾和中间有零的退位减法中，比如500-403和500-133，教师要鼓励学生通过画一画的方法表示自己的思考过程（如图14）。

学生通过画图来理解减法退位的过程，将十位退1借10，百位退1借100的过程，化退位的思维抽象为直观。

（2）操作——支撑算理

借助计数器模型，教师要强化学生对位值制的理解，使学生清晰理解退位的整个过程，让学生通过拨一拨、想一想、说一说将笔算过程展示出来，感受计数器中退位其实是把本来珠子不够的数位，变得珠子更多。

案例2  万以内的退位减法

出示图15，提问1：个位上1减7不够减怎么办？想一想、拨一拨、说一说自己的想法。

请学生上台演示，边操作边交流：个位上不够减，十位上借1个珠子给个位。

接着教师进行操作演示，一边在计数器上拨珠子，一边用数字记录整个过程，深刻理解退去用减、借来用加的整个过程。

提问2：十位上1个珠子表示什么意思？借给个位后要注意什么？

学生通过交流明确十位上1个10等于个位上10个1，10个1和个位原来的1个珠子合起来得到11，在1的上方用11来记录。

提问3：现在个位上怎么减？想一想、拨一拨、说一说。

学生交流后，理解11个珠子减去7个，在计数器个位拨去7个珠子。

提问4：仔细观察，十位上发生了什么变化？又该怎么办？

学生交流自己的想法，根据个位上的经验进行迁移运用。

提问5：百位上退1表示什么意思？十位上借1后发生了什么变化？在学生交流的过程中教师把动态变化的过程用数字来记录，最后在计数器的十位上拨去9个珠子。

学生独立计算后，教师让学生完整地表述整个竖式计算的过程。教师顺势进行小结，强调退位减法的注意点、竖式规范的书写格式以及退位的简捷标记方法。

连续退位的计算，学生的错误率很高，因此在教学中教师要注重将操作演示与抽象算理之间进行勾连，通过学生拨一拨、说一说和教师演示强化，让学生对退位减法的过程建立深刻的表象，有效突破学习的难点。

（3）运用——扎根算理

数学来源于生活，运用于生活，学生对算理的理解需要在生活情境的运用中找到原型，得到巩固、强化、扎根。

案例3  “百以内数加减法”片断

呈现情境：亮亮有4元钱，拿走了3角5分，还剩下多少钱？

学生根据实际情境写出算式：400-35。

学生尝试用人民币模型进行操作，先把1元转化成10角，然后把10角中的1角转换成了10分。

教师提问：刚才转化人民币的过程和减法过程有着怎样的联系？

深入交流：被减数的个位和十位都是0，为什么个位是10减去5，十位上是9减去3？在计算的过程中要注意什么？

通过人民币的情境来理解退位的过程，激活了学生的已有经验，将元、角、分单位的转化与计数单位的转化建立联系，既直观又生动，使学生对算理的理解更加深入。

（4）归纳——内化算理

教师要鼓励学生尝试用不同的方式将计算的算理描述出来，给足时间让他们充分探究、交流、巩固和总结归纳算理。

①颜色区分。竖式中借助不同的颜色可以有效凸显退位的过程、计算的顺序，如图16所示，分别用了两种不同的颜色代表退位的变化和位置值情况。

两种方法都不约而同用不同的颜色突出重点，化解难点。

②填写补白。教师要倡导学生把思维的过程用文字写出来，渗透尝试与猜想的数学思想。比如笔者在“百以内的退位减法”教学中提出数学问题，列出横式“52-17”之后，让学生尝试用列竖式的方法计算，出示图17。

用长方形空白填写位置值，用正方形格子代表退位后数位上数值的变化，这样的留白填写能激发学生的创造思维，主动构建数值变化的准确值，在交流碰撞中理解退位的本质含义。

③斜线演示。通过画图的形式，帮助学生更好地建构退位减法的解题结构，如图18，用画斜线形象地对退位减法的过程进行演示。

教师出示图18①算式，让学生们用自己喜欢的符号，表示出退位减；图18②大部分学生通过知识迁移用画斜线的方式表示退位；图18③，还有少部分学生选择画圈，代表隐藏起来了，代表数值产生了新的变化。

3. 练习设计：从单一到系统

（1）注重培养学生的退位意识

在练习设计方面，如图19，教师应该根据数的位值制意义及数的拆分与组成原理，通过动态图的引导，培养学生的退位运算意识，提高计算的分析能力和思维能力。

（2）注重培养思维的全面性

通过计算打通加减法之间的互逆关系，能培养学生思维的全面性。如图20，同一种算式，教師先让学生完成左图竖式，然后不改变数字而通过改变补白位置，从而让思维走向全面。

总之，从一个退位“点”的问题开始，教师在退位减法的教学活动中要尽量拉长学生的思维时间，不要急于公布计算的结果。通过”变教为学“的课堂设计，学生在探究性学习的过程中可培养思辨、推理的能力，感悟运算算理的一致性。教师要正视学生的问题，关注学生背后隐藏的想法，引导和鼓励学生主动尝试不同维度的“退位计算”，尝试运用数形结合方法，让退位运算意识植入学生的脑海里。教师要让每一个学生都有机会思考，一个会思考的学生可以走得更远。

参考文献：

［1］ 中华人民共和国教育部．义务教育数学课程标准（２０２２年版）［M］． 北京：北京师范大学出版社，２０２２．