大单元背景下的跨学科融合教学的探究

谭新艳

[摘 要] 新课标要求教师丰富教学方式，“探索大单元教学，积极开展跨学科的主题式学习和项目式学习等综合性教学活动”.“勾股定理”一课，将数学与历史学科整合，培养学生多学科综合分析和解决问题的能力.

[关键词]大单元教学；跨学科；勾股定理

基金项目：2022年东莞市年度规划课题“大单元背景下的初中数学与历史跨学科教学的实践研究”（2022GH629）.

新时代召唤新教育，新教育需要新教学.大单元教学是课程的需要，依据《系统论》的基本原理，整体优于部分，整体决定部分，整体大于部分之和，我们需要促进系统内的各构成要素的协同与整合.大单元教学能避免“只见树木、不见森林”的零散，长期如此学生就能见到一片绿洲.

《义务教育数学课程标准（2022年版）》明确指出：学生通过数学课程的学习，适应现代生活，掌握进一步学习的必备基础知识、基本技能、基本思想和基本活动经验.如何达到上述目标？笔者做出如下解释：将数学学习与生活结合，借鉴历史经验完善自己的学习体系.

我们常说，数学来源于生活，生活即数学；我们又说，今天发生的事情将成为历史，生活即历史，那么将历史搬进数学教育是多么的合适.我们可以在数学教学过程中重演历史，站在巨人的肩上，借鉴别人的经验完善自己.课堂中教师带领学生科学地探索历史，引导学生主动体验、建构，积累数学基本活动经验，为长远学习打下基础.

跨学科融合教学的实践

现结合“勾股定理（第1课时）”新授课教学，阐释如何进行跨学科融合教学，增强学生发现问题、提出问题的意识，提升学生分析问题、解决问题的能力.

1.内容分析

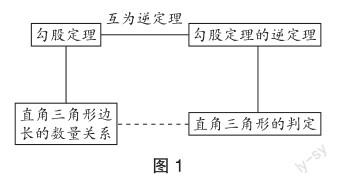
人教版教材八年级下册第十七章“勾股定理（第1课时）”是章起始课，具有统领全章的作用，思想深刻，育人价值高[1].其教材结构如图1.

本校学生在七年级上学期的数学寒假作业中，有一项任务是读一本好书——《奇妙的数学史》，并写一篇500字以上的读后感.从批阅读后感中笔者发现，一位学生对勾股定理印象比较深刻，他借此机会细细揣摩，深入探索了勾股定理这一知识点，并在读后感中写道：“我们每个人都是数学家，因为我们发现问题，并努力尝试解决问题.哪怕这个问题已经被人解答了，但没关系，因为我挑战了自己，经历了由未知到已知的过程，你应该为自己骄傲.”的确如此，对于本课时的教学，我们将采取大单元教学视野下数学融合历史跨学科教学，激发学生自主学习的欲望.

2.教学目标

（1）了解勾股定理的历史背景，掌握勾股定理；体会赵爽发现勾股定理的过程.

（2）能通过割补法构造图形证明勾股定理.

（3）经历“发现—探索—猜想—验证”等学习活动，发展学生的几何直观、逻辑推理等核心素养，让学生感受从特殊到一般、数形结合、转化与化归等思想方法.

3.教学重点、难点

重点：探索并证明勾股定理.

难点：感悟从特殊到一般、数形结合、转化与化归等思想，培养几何直观、逻辑推理等核心素养.

4.教学过程

（1）课前小测，唤醒数学思维

填空：

①在△ABC中，∠B=20°，∠C=70°，则∠A= ，△ABC是 三角形.

②如图2，每个小方格正方形的边长为1个单位，则格点三角形的面积是 .

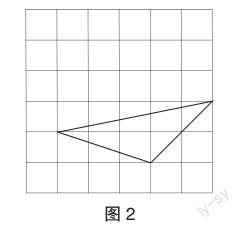
【教学分析】 课前小测的设计意图是唤醒本节课相关联的知识，利用已有的知识解决未知的问题，发展学生的知识迁移能力.学生在学习勾股定理前，已经通过测量、拼图、折纸等活动，证明了三角形内角和定理，学习了直角三角形两锐角互余的性质，学生树立的推理意识以及活动中积累的经验，都为本节课探究和证明勾股定理奠定了基础.第②小题通过“割补法”求格点三角形的面积，发展学生的类比思想，因为本节课在探究勾股定理时，需要求格点四边形的面积.

（2）剧本引入，培养数学兴趣

旁白：相传2500多年前，古希腊著名的哲学家、数学家、天文学家毕达哥拉斯有一次在朋友家做客时，发现朋友家用砖铺成的地面图案（如图3）特别有趣，陷入沉思……

穿着奇特的服装，挂上络腮胡子，扮演毕达哥拉斯的学生一出场，立刻引得全班同学哈哈大笑.“毕达哥拉斯”盯着地板，左看看右看看，兴奋地自言自语道：“好奇妙，这图案中竟含有這样特殊的数量关系，太神奇了！”

【教学分析】 毕达哥拉斯激发了学生的好奇心，学生迫不及待想知道毕达哥拉斯发现了什么.学生带着好奇心，走进历史长河，走进毕达哥拉斯的世界，历经知识的演变.

（3）任务驱动，积累活动经验

教师设计富有挑战性的学习任务，教学时给学生发放一页讲义，讲义上有四幅7×7的格点图（如图4），提出了三个任务：①利用下列网格，画出几个格点正方形；②关于画出的正方形，你发现了什么？③结合图形说说你是如何求这些正方形的面积的.