求解一道“将军饮马”模型问题的三种方法
2024-04-10唐双利
唐双利


【摘要】“将军饮马”是初中数学问题中的一个经典模型,其思想和解决方法也蕴含在诸多的题目中.在两点之间线段最短的定理基础上,如何去求解不是直线的两条线段长度之和的最小值,是此类问题的研究重点.本文探讨一道“将军饮马”模型的典型例题的三种方法,以供参考.
【关键词】初中数学;平面几何;图形变换
在平面几何问题中有一类经典的问题,即图形变换问题,此类问题综合性强,难度大,考验学生对几何图形的处理能力和想象能力.当“将军饮马”模型与图形变换问题融合时,处理的方法也就自然变得多种多样,求解此类问题需要发散思维,从问题的本质出发,就能够解出答案.
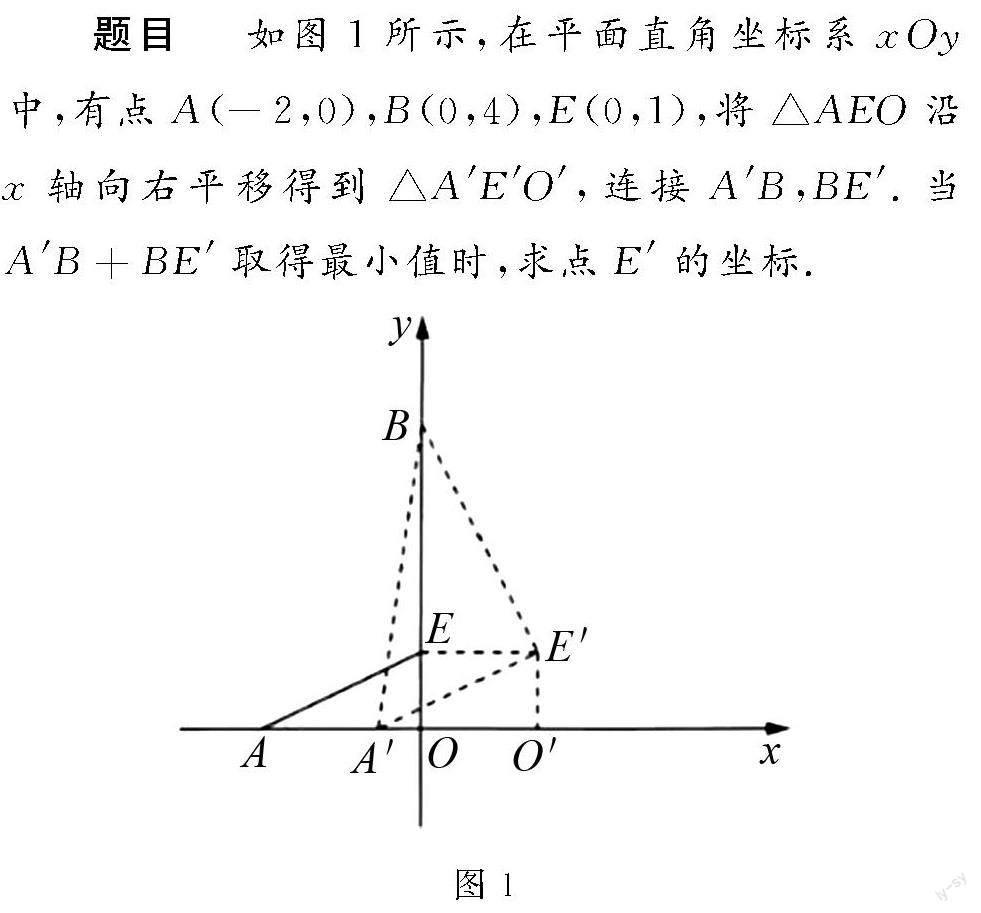
题目 如图1所示,在平面直角坐标系xOy中,有点A(-2,0),B(0,4),E(0,1),将△AEO沿x轴向右平移得到△A′E′O′,连接A′B,BE′.当A′B+BE′取得最小值时,求点E′的坐标.
图1
解法1 利用全等和相似三角形
如图2所示,过点A作AB′⊥x轴,
并使AB′=BE=3.
易证△AB′A′≌△EBE′,
所以B′A′=BE,
从而A′B+BE′=A′B+B′A′.
当点B,A′,B′在同一条直线上时,A′B+B′A′最小,即此时A′B+BE′取得最小值.
易证△AB′A′∽△OBA′,
图2
所以AA′A′O=AB′OB=34,
则AA′=37×2=67,EE′=AA′=67,
所以点E′的坐标是(67,1).
此解法通过利用全等和相似三角形的性质,将题目中的两条线段中的BE′转化为了B′A′,从而通过这两条线段在构成直线时的长度之和为最小值推得原两条线段的长度之和的最小值,本质上是一个等价转化.
解法2 在平面直角坐标系中利用代数方法解得
如图3所示,将点B(0,4)沿射线AE的方向平移AE线段长得点M,则点M的坐标为(2,5),连接BM,易证四边形BME′A′是平行四边形,
则A′B=E′M.
因为点E(0,1),将△AEO沿x轴向右平移得到△A′E′O′,
设AA′=n,则EE′=n,
图3
点E′(n,1),即点E′在直线y=1上.
作点M关于直线y=1的对称点M′,连接E′M′,
则点M′的坐标为(2,-3).
当点B,E′,M′在同一条直线上时,BE′+E′M′最小,即此时A′B+BE′取得最小值.
设直线BM′的表达式为y=kx+b,
则b=42k+b=-3,
解得k=-72b=4,
所以直线BM′的表达式为y=-72x+4.
当y=1时,-72x+4=1,
解得x=67.
所以点E′的坐标是(67,1).
因为题目本身就在平面直角坐标系中,而根据数形结合的数学思想,可以将几何问题转化为代数问题来求解,直接求出直线的表达式,通过对称平移等方法综合解得答案.
解法3 寻找表达式的几何意义
因为点E(0,1),将△AEO沿x轴向右平移得到△A′E′O′,
设AA′=n,则EE′=n,
点A′(-2+n,0),点E′(n,1).
所以A′B+BE′=(n-2)2+42+n2+32.
根据坐标平面上两点间距离的公式不难发现,可将(n-2)2+42+n2+32看成坐标平面上x轴上一动点G(n,0)到定点P(2,4)和Q(0,3)的距离之和.
由此(n-2)2+42+n2+32的最小值转化为GP+GQ的最小值.
作点Q关于x轴的对称点Q′(0,-3),由“两点之间,线段最短”可知,当点G运动到PQ′与x軸交点位置时,此时GP+GQ的值最小.
直线PQ′对应的函数关系式为y=72x-3,与x轴的交点为(67,0).
所以,n=67,
所以点E′的坐标是(67,1).
此解法先利用平面直角坐标系写出了题目中所求最值的代数形式,与解法2不同的是,此解法将代数转化为了几何,利用代数表达式的几何意义,将问题简化,从而找到答案.
结语
以上三种方法从不同的角度解决了这道典型例题,总的来说,对于“将军饮马”模型的问题,最重要的数学思想就是数形结合,两者相互补充,就能够使问题的解决既简单,直观化,又能够避免复杂的计算.同时还要充分利用全等和相似三角形这一重要的几何工具,来得到所需条件.
