梳理图形关系 建立内在联系

郑丽君 章拥军

【摘   要】《义务教育数学课程标准（2022年版）》提出：要整体把握教学内容，注重教学内容的结构化。在“平面图形的面积”总复习的教学中，教师可通过“以转化思想为契机，引导溯源求联；以几何直观为支架，启发本质关联；以空间想象为载体，发现内在关联”等方式，帮助学生用整体的、联系的、发展的眼光发现数学知识之间的内在联系，感悟数学学习背后隐藏的思想本质。

【关键词】平面图形的面积；面积计算公式；总复习；内在联系

《义务教育数学课程标准（2022年版）》提出：要整体把握教学内容，注重教学内容的结构化。在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。平面图形的面积是小学数学的重要教学内容。在小学阶段，学生需要掌握长方形、正方形、平行四边形、三角形、梯形和圆形的面积计算方法。这些教学内容依照螺旋上升的原则，编排在三年级到六年级的教材中。因为学习时间的跨度很长，所以学生很難整体把握和主动建立这些内容之间的联系。六年级下册有关“平面图形的面积”的总复习，是帮助学生将相关知识结构化的重要契机。教学时，教师要引导学生经历不同平面图形面积计算公式的整理、归类过程，建立知识网络，体会和掌握转化、类比、数形结合等数学思想。

基于以上认识，教师展开了“平面图形的面积”总复习的教学实践，用三个探究任务，引导学生将零碎的数学知识整理成一个知识系统，让他们通过观察、想象、思考、交流，发现平面图形的面积计算公式推导过程中的特殊与一般的关系，感受平面图形之间特殊与一般的关系，体会平面图形的外在特征与内部量的属性之间统一协调的关系。学生在学习过程中，经历了用整体的、联系的、发展的眼光发现不同面积计算公式之间存在着密切联系的过程，使这些知识逐步在头脑中形成具有统一美的严谨系统，产生对数学内在高度统一性的认识，以及对数学思想方法的感悟。

一、以转化思想为契机，引导溯源求联

“平面图形的面积”的总复习是一节复习课。在前面几年的学习中，学生已经陆续学习过本节课所涉及的不同图形面积的知识点，因此，在进入课堂教学前，教师先让学生对相关知识进行了前置性整理和复习。教学时，教师引导学生回顾已学习的平面图形的面积计算公式的推导过程，厘清各个公式的来龙去脉，建立它们在知识结构上的内在联系，并通过探究任务一，体会和掌握转化的数学思想，形成对知识的一般性理解。

【教学片段1】

教师按照教材编排的先后顺序，分别呈现长方形、平行四边形、三角形、梯形和圆形，引导学生对教材中的相关内容进行梳理，交流平面图形的面积计算公式及其推导过程，唤起学生的原认知。

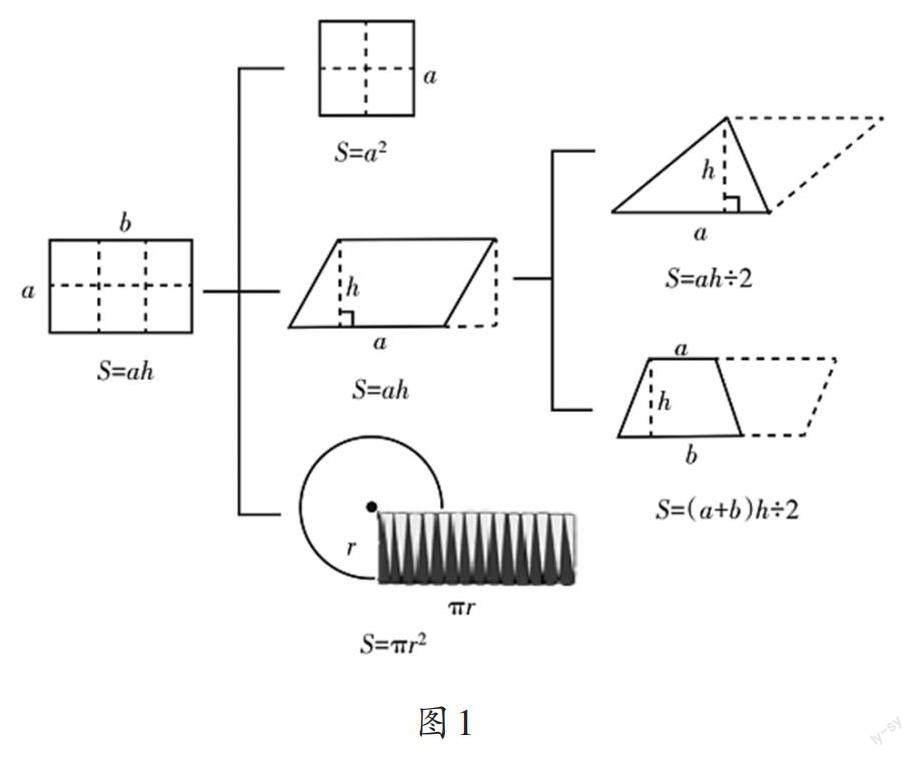
师：课前，大家整理了有关平面图形面积的相关知识。现在，我们一起来看看这个同学的整理过程，你看懂了什么？（如图1）。

生：他是按照平面图形的面积公式的推导过程进行整理的。

师：这些平面图形的面积计算公式是怎样推导出来的？你能选择其中一个图形说一说吗？

生：我选择介绍平行四边形。推导平行四边形的面积计算公式时，我们先通过“剪、移、拼”等方法，将平行四边形转化为长方形，然后根据长方形的面积计算公式得出平行四边形的面积计算公式。

生：在将平行四边形转化为长方形时，我们用到的方法是割补法。而在推导三角形的面积计算公式时，我们是把两个完全一样的三角形拼成一个平行四边形，再根据平行四边形的面积计算公式推导出三角形的面积计算公式，这种方法叫作倍拼法。在推导梯形的面积计算公式时，我们也用了倍拼法。

生：推导圆的面积计算公式的过程比较复杂。我们先把一个圆沿半径切割成若干等份，再把它们拼成一个近似的长方形，然后根据长方形的面积计算公式得出圆形的面积计算公式。

师：谁还记得长方形和正方形的面积计算公式是怎样推导出来的？

生：我记得归纳长方形的面积计算公式时，我们把若干个1平方厘米的小正方形摆在长方形上，发现每行摆的个数相当于长，摆的行数相当于宽，所以长方形的面积=长×宽。

生：归纳正方形的面积计算公式和归纳长方形的面积公式使用的方法是一样的。只是长方形的长和宽在正方形中是一样的，都是正方形的边长，这样我们就得到了正方形的面积计算公式。

师：在这些图形中，你认为哪个图形的面积计算公式是最基本的？

生：我认为最基本的是长方形的面积计算公式，因为其他图形的面积计算公式都是由长方形的面积计算公式推导出来的。

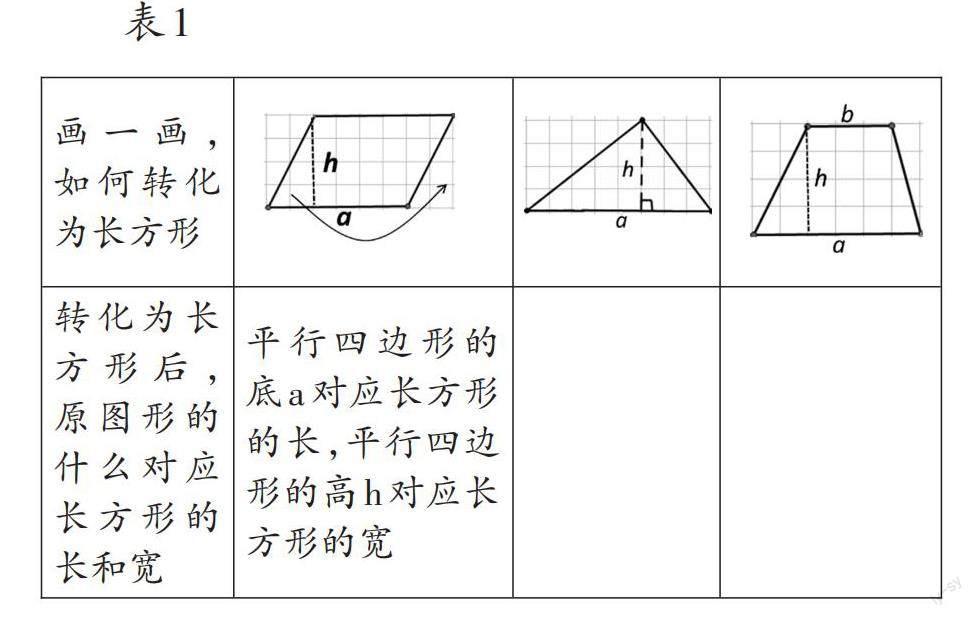
师：在学习不同图形的面积计算公式时，只有平行四边形是直接转化为长方形计算面积的，转化过程如表1。如果大家认为长方形的面积公式是最基本的，我们学过的其他图形的面积公式都可以通过长方形面积公式推导出来，那是不是说这些图形本身也都可以转化为长方形呢？请大家完成探究任务一：将三角形和梯形转化为长方形，并将表1补充完整。

学生先独立思考、小组交流，再全班汇报。

师：三角形可以怎样转化为长方形？

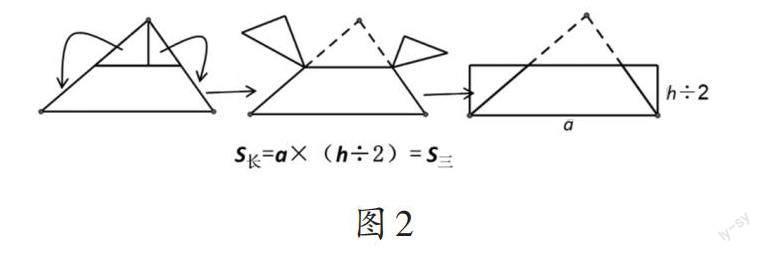
生：我们小组把三角形的上面部分通过分割和移补转化为长方形（如图2）。

生：我们小组把三角形的左右两个角通过分割和移补转化为长方形（如图3）。

生：其实，梯形也能通过类似的分割、移补转化为长方形。

上述学习活动使学生对平面图形的面积计算有了整体性的认知，在梳理中看到转化对平行四边形、三角形、梯形、圆的面积计算公式推导的作用，并通过再现各种平面图形的面积计算公式的形成过程，帮助学生在梳理知识的过程中获得对平面图形的面积计算方法的结构化认识，形成几何直观、推理意识。

二、以几何直观为支架，启发本质关联

从形式上看，平面图形的面积公式各不相同，但通过图形的直观变化，可以将它们统一联系起来，从而帮助学生形成平面图形的面积计算的知识结构。

【教学片段2】

师：刚才，我们梳理了各种平面图形的面积计算公式，这些公式之间有怎样的联系呢？

教师利用课件动态演示，让学生直观观察图形的变化：一个梯形，上底开始慢慢缩短，缩短到0时，它“变成”了一个三角形；接着，它的上底再次“出现”并慢慢拉长，当上底的长度等于下底时，它“变成”了一个平行四边形；然后，在平行四边形的基础上，它的“上底”从原来的位置平移到“下底”的正上方，“变成”两组对边相互垂直的状态，成了一个长方形；长方形继续变化，当长方形的长缩短到与宽长度相等时，它就“变成”了一个正方形。

师：刚才的三角形、平行四边形、长方形等，都是从梯形“变化”而来的，那么，用梯形的面积公式是否也能计算出其他平面图形的面积呢？

生：有可能可以。

师：请大家完成探究任務二：验证是否可以用梯形的面积公式计算其他图形的面积，完成表2。

学生先独立思考、小组交流，再全班汇报。

生：可以把长方形和平行四边形想象为上下底相等的梯形，用梯形面积公式（a+a）×h÷2计算得出面积，并将它进一步化简，得到（a+a）×h÷2=2a×h÷2=a×h，这正是平行四边形的面积公式。如果高和宽一致，就是长方形的面积公式S=ab。

生：同样，把三角形想象为上底是0的梯形，就可以得到（a+0）×h÷2=a×h÷2。

生：我们原来学过，圆可以通过“化曲为直”转化为长方形。

生：我有一个疑问。如果只用一个梯形的面积公式就能计算出这么多平面图形的面积，那我们为什么不一开始就学梯形的面积公式？这样不是只记这一个公式就可以了吗？

师：这个同学太会思考了！

教师出示华罗庚的名言：先学习、接受“由薄到厚”，再消化、提炼“由厚到薄”。

师：谁能用华罗庚的名言来分析一下这个同学的疑惑？

生：先分开学习每个平面图形的面积推导，这是知识“由薄到厚”的过程；再建立这些平面图形的面积公式之间的联系，找到用梯形的面积公式来计算其他平面图形面积的方法，这是知识“由厚到薄”的过程。

在上述学习活动中，教师通过课件动态演示，借助探究任务帮助学生理解梯形、三角形、平行四边形、长方形和正方形面积公式之间的内在联系。

三、以空间想象为载体，发现内在关联

空间想象是一种重要的能力。在复习阶段，引导学生结合动态演示，想象平面图形的动态形成过程，可以促进学生体会不同平面图形之间的关联，为他们后续的学习打下基础。

【教学片段3】

师：我们知道“点动成线，线动成面，面动成体”，请大家完成探究任务三：想象一下，线通过怎样的运动，会形成这些基本的平面图形？先想象一下长方形是怎样形成的。

生：以一条线段为长，将这条线段向上平移宽的高度，就形成了长方形。

生：也可以这条线段为宽，向左或向右平移长的距离，形成长方形。

教师用微课展示其他图形的动态形成过程，并请学生结合动态演示过程思考：除了我们已经学过的平面图形的面积计算公式，这些平面图形的面积还有其他的计算方法吗？拓展介绍：从运动的角度思考这些平面图形的面积，它们的面积还可以通过“中位线”的长度求得。那什么是“中位线”？“中位线”怎么求呢？大家可以课后再进行探索，如果找到了答案，我们再来交流。

以上教学过程，教师通过三个探究任务，引导学生对平面图形的面积进行整理和复习。在探究任务一中，学生以转化思想为契机，发现了平面图形面积推导过程之间的特殊与一般关系；在探究任务二中，学生以几何直观为支架，挖掘出平面图形之间的特殊与一般的内在关系；在探究任务三中，学生以空间想象为载体，通过课内想象和课外探索，初步认识了平面图形的外在特征与内部量的属性之间的统一协调关系，为后续几何的学习打下坚实的基础。这样的教学，能够帮助学生用整体的、联系的、发展的眼光发现数学知识之间的内在联系，感悟数学学习背后隐藏的思想本质。

参考文献：

［1］袁春胭，王霞. 图形与几何中数学语言表达能力发展路径：以人教版教材《平面图形面积的复习》一课为例［J］. 教学月刊·小学版（数学）， 2022（3）：21-23.

［2］张丹，刘晓.“问题引领学习”的构建及单元教学研究［J］.数学教育学报，2018，27（5）：42-47.

［3］刘莉.见木又见林：小学数学结构化教学的思考与实践［J］.数学之友，2018（3）：26-29.

［4］王小权. 翻转复习 共学悟法：“‘平面图形面积的总复习”导学设计及实践［J］. 教学月刊·小学版（数学），2019（1/2）：34-36.

（1.浙江省杭州市桐庐县叶浅予建兰学校 2.浙江省杭州市桐庐县开放大学）