经历多元表征，发展模型意识

王立

【摘   要】模型意识主要是指对数学模型普适性的初步感悟。建立模型的过程其实就是将实际问题数学化、同类问题模型化的过程，这个过程一般需要通过数学化的多表征来实现。教师结合人教版教材三年级上册“归一问题”的应用练习，对数学表征在学生模型意识发展中的应用及意义进行分析和实践，通过“从情景表达到关系理解，借助语言表征感受模型；从数据分析到图式表达，借助图像表征理解模型；从文字表述到操作活动，借助动作表征具化模型；从形象表述到抽象表达，借助形式表征感悟模型”，引导学生在解决“归一问题”的过程中，经历不同的表征体验，丰富对数学模型的建构，在帮助学生解决问题的同时，发展其模型意识。

【关键词】数学表征；模型意识；归一问题

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）指出：模型意识主要是指对数学模型普适性的初步感悟。应用模型意识的基本途径是知道利用数学模型来解决同一类问题，然后有意识地用数学的概念与方法解释或解决现实生活中大量与数学有关的问题。因此，建立模型的过程其实就是将实际问题数学化、同类问题模型化的过程。要让学生体会数学与生活之间的联系，要引导学生将情境问题转化为数学问题，在所要建立的数学模型与自身已有的数学认知之间建立联系，而这个过程一般需要通过数学化的多元表征来实现。

一、数学表征在发展学生模型意识中的意义

数学学习中，对概念、法则、运算等方面的学习，既包括内隐的心理层面的知识整合与建构，也包括外显的能够呈现认知过程和认知结果的多样化数学表达，这些过程即为数学表征。学生只有获得这两个方面的体验，才能真正掌握知识的学习。

根据数学表征中的不同要素，可以将数学表征分为直观形象表征和抽象形式表征两类。直观形象表征一般包括动作表征、情景表征、图像表征等，抽象形式表征则一般包括符号表征、算式表征、结构图表征等。不同的数学表征体现着学生对问题理解和解决过程的结构化表达水平，反映了他们不同的思维状态与水平。在教学过程中，教师需要关注各种表征方式的特点，结合问题关联不同的表征方式，帮助学生从整体上把握解决问题的关键点，建构起相关问题的数学模型。

2022年版课标提出发展小学生的模型意识，强调学生对数学模型普适性的初步感悟，引导学生经历应用模型或解决问题的过程，从而获得建构模型的经验。学生要发展的模型意识一般会涉及模型的丰富表达形式——外在表征、模型的心理表达（表象）形式——内在表征，以及内外表征之间的转化。因此，要将2022年版课标提出的目标要求落实到教学实践中，需要教师在学生建构模型的过程中，将多种表征有机融合起来，发挥各种表征特有的认知、感悟价值，助力学生模型意识的发展。本文结合人教版教材三年级上册“归一问题”的应用练习，对数学表征在学生模型意识发展中的应用及意义进行分析和实践。

二、数学表征在“归一问题”模型建构中的应用

“归一问题”是指含有“归一”数量关系的问题，这类问题中，每份量是一定的，总量与数量成正比例关系。解答“归一问题”时，在用除法求出每份量后，若通过“每份量×数量”求总量即为“正归一”，若通过“总量÷每份量”求数量则为“反归一”。“归一问题”是一种典型的问题解决数学模型，是小学阶段理解数学和生活的联系，分析和解决问题的重要内容。三年级学生在学习“归一问题”后，积累了较为丰富的收集信息、分析信息的能力，并能利用“画图”等方式理解“归一问题”的基本特征。下面，笔者结合相应的练习，从数学表征的角度对“归一问题”模型的建构与应用过程进行分析和实践。

（一）从情景表达到关系理解，借助语言表征感受模型

语言表征即利用口头语言描述模型结构的表征方式。将现实生活情境转化为数学问题，是建立“归一问题”模型的起点，这要求学生利用自己的语言把现实情境转化为数学问题，并通过口头表达对情境中的“归一问题”结构进行阐述。在这一过程中，学生需要对情景问题中的信息进行观察、思考、分析和处理，这是感知“归一问题”模型的基础。

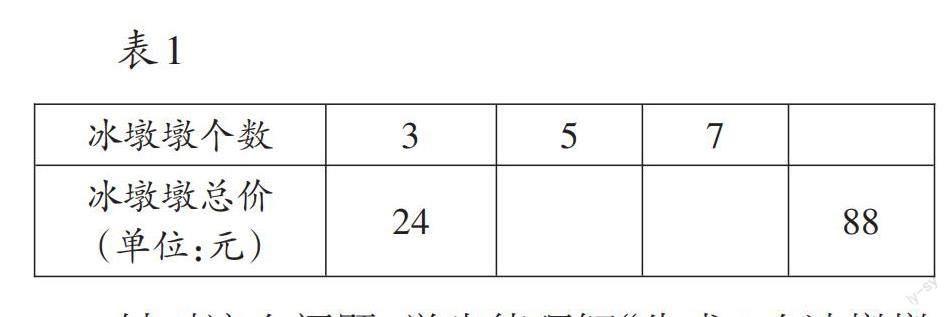
问题：三个小朋友一起到商店买吉祥物“冰墩墩”。丁丁要买3个，红红要买5个，明明要买7个。已知3个冰墩墩的价格是24元，求出5个、7个冰墩墩的价格，以及88元可以买几个冰墩墩（如表1）。

針对这个问题，学生能理解“先求1个冰墩墩的价格，再求出几个冰墩墩的价格或能买几个冰墩墩”的解题过程。但仅仅停留在求解层面，对学生理解“归一问题”模型是远远不够的。教师需要引导学生用数学语言把解决问题的关键点表述出来，强化学生对“归一问题”模型结构的感知。教学中，教师要在学生解决相应问题后，组织学生讨论：解答“5个、7个冰墩墩的价格”和“88元可以买几个冰墩墩”这两个问题的思考过程有什么相同的地方？学生经过讨论发现：解决这两类问题都要先算出冰墩墩的单价。这一学习过程引导学生通过口头交流，借助语言表征的方式凸显解决问题的关键点，体现“归一问题”中“一份量”的重要性。

（二）从数据分析到图式表达，借助图像表征理解模型

受认知水平和思维方式的局限，小学生的抽象思维能力较弱，他们需要借助图形等直观形象进行表征，由此理解模型。对三年级学生来说，“归一问题”的结构比较抽象，且由于提供的数据不同，会产生不同的模型结构（正归一、反归一），这给一部分学生的学习带来了困难。因此，教师在课堂上要引导学生用画图的方式对问题进行结构化表达，从而让学生理解“归一问题”模型的基本结构。

问题：王阿姨4分钟包了128个馄饨。照这样的速度，王阿姨8分钟能包多少个馄饨？

在探究这一问题的过程中，教师要鼓励学生用文字或画图的方式将自己的想法表达出来。学生的想法主要有以下两种。

第一种（如图1）：先算1分钟包多少个馄饨，再算8分钟可以包多少个馄饨，即先算“一份量”，再求“总量”。

第二种（如图2）：学生发现8分钟里面有2个4分钟，于是利用时间的倍数关系，把“4分钟包了128个馄饨”看作“一份量”，算这样的2份，就是8分钟包的馄饨数。

学生通过画图的方式对包馄饨的情境进行“转译”，发现要解决“8分钟包多少个馄饨”的问题，既可以“先算1分钟包多少个馄饨，再算8分钟可以包多少个馄饨”，又可以“先把4分钟包128个馄饨看作1份，再算2份可以包多少个馄饨”。虽然这两种方法不同，但它们都是在思考“一份量”是多少，再在此基础上算出“总量”。在画图的过程中，学生能够通过具象化的“图像表征”，直观感受到“归一问题”的多样结构，丰富对此类数学模型的认知。

（三）从文字表述到操作活动，借助动作表征具化模型

动作表征是指通过动作反应对知识进行表征。有些数学模型的构建需要通过动作表征进行描述，而一些复杂问题同样需要通过操作活动，借助动作表征来理解数量关系，从而厘清解决问题的关键点。“归一问题”中也有一些相对复杂的问题，需要学生借助操作活动厘清关系，并将数学模型具体化，进而解答问题。

问题：周末，小聪和小明两家人去美术馆参观。已知2名成人和1名儿童需要门票25元。现在有4名成人和2名儿童，需要门票多少元？

在这个问题中，由于成人与儿童的门票价格不同，学生不能算出成人门票和儿童门票的单价，这给他们解决此问题带来了困难。此时，教师在黑板上呈现人物图片，让学生用这些材料进行操作活动。学生通过操作，发现可以把2名成人和1名儿童看作一个整体，那么4名成人和2名儿童就可以组成2个这样的整体，此时再解决这个问题就简单多了。

解决买票问题的关键是要把“每份量”从一个、一组上升到多个对象组成的整体。因此，教师要利用可以移动的图片，引导学生在操作活动中感受数学模型的结构，丰富“归一问题”的模型结构，帮助学生积累解决“归一问题”的活动经验。

（四）从形象表述到抽象表达，借助形式表征感悟模型

所谓形式表征，就是运用符号、数字及结构化的图式来表达数学结构。学生在构建“归一问题”的模型时，往往只记表象不知内涵。这是因为“归一问题”的外显特征比较容易识别，结构中隐含的本质属性卻不易发现。所以教师要帮助学生经历符号、数字以及结构化图式等形式表征的过程，让他们发现不同情境问题中的相同数学结构，理解“归一问题”的本质属性。这一过程不是在某个环节中能够完成的，而是要体现在整节课的教学过程中。

比如，学生解决了“买冰墩墩”“包饺子”等问题后，既有了把现实情境转化为自己的语言来理解的经验，又有了利用图像表达现实情境、理解图式与现实情境之间关系的经验。此时，教师要将解决这些问题的算式以及思考过程中的关键点呈现在黑板上，围绕这些学习素材，引导学生梳理知识之间的关联点，并借助符号、数字以及结构化的工具进行整理归纳，形成思维过程的结构化。

如图3所示，图中的算式与图式关系都是在分析基础上得到的。学生通过对黑板上内容的观察、思考、比较、联系，发现“归一问题”中的“一”可以是一个的量，可以是一组的量，还可以是一个整体。这样的整理归纳借助形式化的表征，能够帮助学生厘清“归一问题”的模型结构，同时有助于学生将单一的形象思维转化为整体的形式化思维，真正理解“归一问题”模型的内涵。

总之，要让学生感悟数学模型的本质，需要引导学生进行多元数学表征。通过不同表征之间的互译、联结，从复杂的情景中舍去一切非本质属性，得到探究问题的一般模型，是学生发展模型意识必须经历的过程。

参考文献：

［1］席爱勇，李宾.数学多元表征学习的理论与实践［M］.南京：南京大学出版社，2018.

［2］程红霞.以多元表征学习深化学生的数学理解［J］.小学数学教师，2021（10）：12-16，2.

（杭州师范大学附属嘉兴经开实验小学）