基于模型视角 凸显单位“1”

薛群

【摘   要】在小学阶段，有关分数乘、除法的“解决问题”是学习的难点。教师可引导学生通过“表达单位‘1，借助图式模型理解关系；变换单位‘1，借助模型理解数量关系；统一单位‘1，解构模型来解决问题”等过程，提升问题分析技巧，提高对分数意义的理解与应用水平，改善对分数问题的认知结构，发展数学思维。

【关键词】模型；单位“1”；分数问题

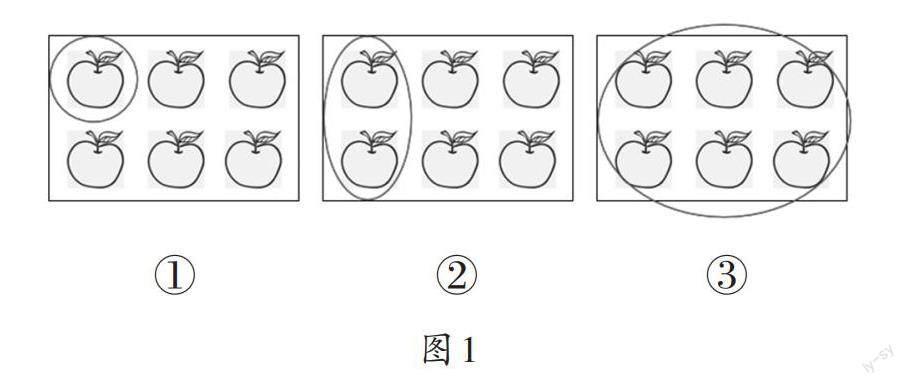
在小学阶段，“1”有两方面含义。一是具体量的1，即自然数的基本单位，几个1就是几；二是抽象概念的1，即单位“1”。一个物体、一个计量单位或是一些物体等都可以看作一个整体，用1来表示。自然数1是单位“1”认识的基础，同时单位“1”的认识，又是数学抽象认知的开端。小学阶段是学生的认知从自然数1向单位“1”过渡的关键时期。教师可以图1为例，引导学生理解从自然数1到单位“1”的发展过程。

如图1所示，三幅图中的“1”具有不同的含义：①号图将1个苹果抽象为1，表示自然数1，图中有6个苹果，表示6个1；②号图将2个苹果看作1份，此时原来的6个苹果就成了3份，即3个1份；③号图将6个苹果看作一个整体，也就是分数认识中所说的单位“1”，此时表征1个苹果要用分数?。从以上变化过程不难看出，建立“1”视角的本质是人们在与情境的互动中，根据不同对象或解决问题的需要而给出的数学抽象的过程。

建立单位“1”是认识分数的起点，也是解决分数问题的基础。然而，在教学实践中，时常存在学生对单位“1”的理解不透彻、套用形式化的数量关系、借助机械性的解题方法等问题。基于上述认识，笔者以人教版教材六年级上册“分数乘法”“分数除法”单元中的“解决问题”为例，从数学模型出发，引导学生着眼于单位“1”的厘清与建构，探究解决分数问题的基本策略。

一、表达单位“1”，借助图式模型理解关系

解答分数乘、除法问题的关键是能准确找出单位“1”。那么，如何从问题情境中理解单位“1”，再从单位“1”入手，把握相应的数量关系呢？教学中，教师可以引导学生借助“图形”的表达，将文字信息转化为图式信息，于图式模型中理解相应的数量关系。

（一）利用面积模型，理解整体与部分的关系

当分数表示整体与部分的关系时，对这一关系的分析就成为解决分数问题的关键，能使许多分数问题的解答变得简单明了。

【例1】一根绳子长6米，剪去了?，剪去了几米？

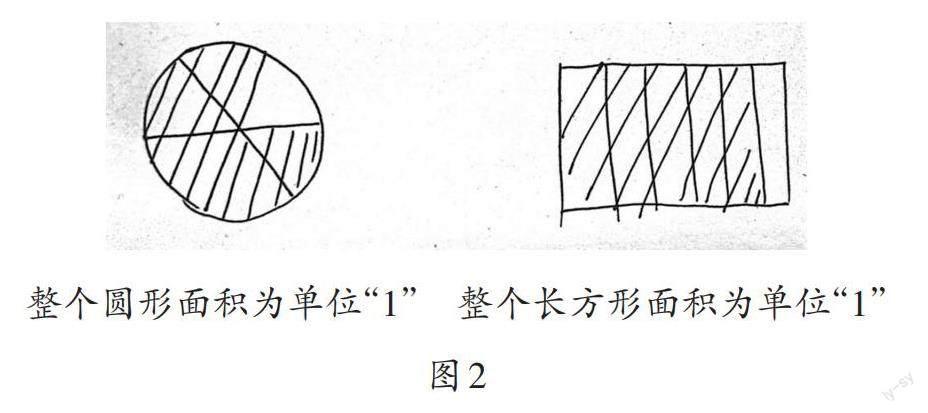
例1中，“一根绳子”是整体，“剪去的”为部分，并且隐藏了另一部分，即“剩下的”。教学时，可以追溯到分数的意义：把“一根绳子”（整体）平均分成6份，“剪去的”（部分）是其中的5份，“剩下的”（部分）是其中的 1 份。这样学生自然就能联系到是把整体看作单位“1”。当引导学生用图形表示出绳子“总长”与“剪去部分”的关系时，除了让学生用线段图表示外，还可以让学生用面积模型图（如图2）来表示。这不仅能强化整体（单位“1”）与部分之间的关系，还能丰富学生的表征方式。

（二）利用集合模型，把握变与不变的关系

当分数表示分率时，需要分析相应分数所表示的意义，把握“分率”的本质，将信息背后可变的量与不变的关系表达出来，并应用关系的不变性来解决相应的问题。

【例2】植物园里有120棵桃树，是杨树的?，杨树有多少棵？

解决此问题的关键是厘清?的含义。“杨树的?”，就是把“杨树的棵数”作为一个整体（即单位“1”）平均分成4份，其中的3份是桃树。由此，得到相应的数量关系：桃树的棵数÷3×4=杨树的棵数。学生解答问题时，可先根据桃树的棵数算出1份的量，杨树有这样的4份，所以桃树的棵数×4就等于杨树的棵数。若辅之以图式，则可以集合图（如图3）的形式加以表征。从图中信息可知，桃树棵数是杨树棵数的?，所以它们之间始终是3份和4份的关系，只是杨树棵数会随着桃树棵数的变化而变化。现在已知3份的量，即知道单位“1”的量的?是120棵，就可列式[120÷34]，求得单位“1”的量。

（三）利用线段模型，厘清比较量与标准量的关系

分数问题中有一类是量与量之间的比较问题，解答此类问题，需要正确把握比较量与标准量（单位“1”），厘清两者之间的关系。

【例3】妈妈买了一件衣服，原价是240元，现价比原价便宜了?，现价是多少元？

解答此问题时，很多学生不清楚应该把谁看作单位“1”。因此，教师教学时要从分数?的意义出发，利用线段模型，帮助学生理解题目中的单位“1”是谁。教师可以引导学生通过分析线段模型（如图4）来理解题目中?表示的意义：“便宜的?”是“原价的240元”平均分成3份后，“现价”处用虚线表示的少的这1份，即与原价相比，现价是在原价3份的基础上减少1份。因此，“原价的240元”是本题的单位“1”。

二、变换单位“1”，借助模型理解数量关系

分数问题中，单位“1”的转化属于相对较难的问题。解答此类问题的关键，是正确合理地确定和转化单位“1”的量。

例如：甲数比乙数多?，乙数比甲数少?。在“甲数比乙数多?”这段信息描述中，单位“1”为乙数；在“乙数比甲数少?”这段信息描述中，单位“1”为甲数。碰到这样的问题，学生容易混淆单位“1”。为帮助学生理解单位“1”转换的过程，理解相互之间的关系，教学中，教师可以采用以下两种方式。

（一）“分总”关系转化，理解部分量与部分量的倍数关系

【例4】某班缺席人數是出席人数的[15]，缺席人数占全班人数的几分之几？

让学生根据题意用模型表示（如图5）。

题目中的[15]表示把出席人数平均分成5份，缺席人数就是1份。再根据“总量=部分量＋部分量”，可得总量为（1+5）份，把以部分量为单位“1”转化为以总量为单位“1”，即可得到“缺席人数是全班人数的? ”。

【例5】某车间男职工人数占车间总人数的[4/7] ，车间男职工人数比女职工人数多几分之几？

让学生根据题意用模型表示（如图6）。

依据本题的模型可以看出，把车间总人数平均分成7份，男职工占了其中的4份，女职工占了（7-4）份。因此，男职工人数比女职工人数多了（4-3）份，即男职工人数比女职工人数多了[4-37-4=13]。

（二）“续变”关系转化，理解单位“1”的变与不变

【例6】甲数是乙数的? ，乙数是丙数的?，丙数是甲数的几倍？

让学生根据题意用模型表示（如图7）。

根据甲数、乙数、丙数三个数之间的关系，可将最小量甲数视为单位“1”，那么乙数就是甲数的[3/2]，而乙数又是丙数的?，由此可得出丙数的?=甲数的[3/2] ，即丙数是甲数的[32÷34=2]（倍）。类似这样的问题，都可以通过先确定某个量为单位“1”，然后进行信息的转化，找到其他量与单位“1”的量的关系，借单位“1”的量来统一其他量进行解决。

可见，在教学分数“解决问题”的过程中，根据题目信息，寻求具体数量与分率的对应关系，对“1”进行转化，使较为隐蔽的关系变得明朗，是一种相当重要的解决问题的策略。

三、统一单位“1”，解构模型来解决问题

当将分数乘法与分数除法整合起来综合运用时，会产生一些较为复杂的分数问题。解答此类复杂分数问题，需要深挖信息，理解题目中部分量与单位“1”、部分量与部分量之间的关系。在教学实践中，教师主要可以采用以下两种方式。

（一）回归情境，找出信息之间的对应关系

通过简单分数问题的学习可知，部分量对应部分量与单位“1”的分率，而它们相除的值则是单位“1”对应的量。那么，解答复杂分数问题时，是否可以此为突破口去分析相关信息，从而找到合适的解题路径呢？

【例7】一批零件，王师傅每天做 60 个，做了2天后，李师傅帮忙一起做，4 天后全部完成，这时李师傅做了全部零件的?。这批零件一共有多少个？

让学生根据题意用模型（线段图）表示（如图8）。

根据题目的情境，可以厘清这几条信息。（1）将“一批零件”看作单位“1”。（2）全部工作量可以分成三个部分：王师傅单独做的部分（每天60个，做了2天）、两人同时工作时王师傅做的部分（4天的量）、两人同时工作时李师傅做的部分（4天，全部工作量的? ）。（3）要解答的问题：单位“1”的量是多少？分析上述相关信息可知，李师傅完成了全部工作量的?，那么，王师傅完成的就是全部工作量的?。又因为王师傅完成的工作量可以用“工作效率×工作时间”来计算，即60×（2+4）=360（个），所以要求单位“1”的量，可以用[360÷23]进行计算。

（二）梳理关系，解构量率的依存关系

分数与除法、比之间有着密不可分的关联。“比”相关知识的学习，为学生解决复杂的分数问题提供了更为多元的解题思路。对于某些问题，完全可以利用比与分数的联系，结合量率间的依存关系进行解答。

【例8】花园里有牡丹花 36 朵，  月季花朵数是牡丹花朵数的?，凤仙花朵数是月季花朵数的?。凤仙花有多少朵？

让学生根据题意用模型（线段图）表示（如图9）。

解决这类较复杂的分数问题，可以借助线段图进行分析。月季花朵数是牡丹花朵数的?，即把牡丹花朵数看作单位“1”，将其平均分成3份，月季花朵数即为2份；凤仙花朵数是月季花朵数的?，即把月季花朵数看作单位“1”，将其平均分成2份，凤仙花朵数即为1份。从线段图中可以看出，凤仙花朵数、月季花朵数、牡丹花朵数的比是1∶2∶3，那么，已知牡丹花朵数为36朵，根据比的基本性质，月季花朵数为24朵，凤仙花朵数为12朵。

综上所述，分数乘、除法“解決问题”对于学生来说较为抽象，理解起来也比较困难。教学中，教师要抓住分数意义这一本质，引导学生把握题目中的单位“1”，结合图式架构单位“1”模型，厘清部分量与单位“1”的量的关系，从而解决问题。

（浙江省嘉兴市海盐县通元小学）