把握度量本质 促进量感发展

黄碧峰

【摘   要】度量在数学学习和应用中具有重要的意义和价值，既是学生形成量感的起点，又是检测学生量感水平的标尺，是培育学生量感的重要载体。结合“认识面积”的教学实例，从度量的内涵、度量对象的属性、度量标准的优化、度量活动的设计以及度量结果的精确五个方面对度量进行深入阐述，进而把握度量本质，促进量感发展。

【关键词】量感；度量；核心素养

在我国小学数学课程中，“数感”与“量感”的概念长期处于模糊状态。《义务教育数学课程标准（2011年版）》中只有“数感”概念而无“量感”概念。然而，很多国家（如新加坡、加拿大、美国）的中小学数学课程中都设置了以“度量”或“测量”为主线的课程内容，以凸显量感的重要性。《义务教育数学课程标准（2022年版）》中新增了“量感”这一核心素养的主要表现，并指出：“量感主要指对事物的可测量属性及大小关系的直观感知……建立量感有助于学生养成用定量的方法认识和解决问题的习惯，是形成抽象能力和应用意识的经验基础。”［1］。

量感的建立需要经历“工具度量—复合表象—度量经验—合理估测”四个步骤，是一个循环往复的过程。其中，工具度量是量感建立的基础，利用工具度量能使学生在实际度量过程感悟刻画物体某一方面的属性（如面的大小）的相关经验，从而形成相应的度量经验，这些度量经验可以支撑学生对物体进行合理的估测，而估测得准确与否，又要借助工具度量进行检验，进而判断学生的量感水平。由此可见，度量既是学生形成量感的起点，又是检测学生量感水平的标尺，是培育学生量感的重要载体。本文以人教版教材三年级下册“认识面积”为例，在探讨度量内涵的基础上，说明度量的核心要素，具体包括度量对象、度量标准、度量活动和度量结果。

一、度量的内涵

量可以分为两类：离散的量和连续的量。离散的量的基本度量方法是“数数”，即数出一堆物体由多少个独立个体构成，以“1”为度量单位，如1把伞、1间房和1个桃。而连续的量的度量需要规定统一的“度量单位”，借助度量工具进行测量［2］。对于不方便直接度量的量，如速度、体积等，则可以通过计算得到度量的结果。

相应地，度量也可以分为两类：第一类是对事物个数和顺序的度量（指自然数），需要通过抽象得到度量结果，是人类思维的结果；第二类是生活中常见量的度量，需要借助工具得到度量结果，是人类实践的结果［3］。本文讨论的是第二类度量，即将一个待测多少或大小的量与该属性的一个标准量或单位量进行比较，从而得到该量的量值的过程［4］。简单来说，就是度量事物含有“多少个”标准量或单位量。

综上可知，数是对度量结果的表达，度量是数学的本质，是人们创造出来的数学语言，是人们认识、理解和表达现实世界的工具［5］。

二、度量对象的一些属性

（一）度量对象具有可测量

度量对象聚焦于客观事物的大小、多少、长短等有关的计量问题，这说明度量对象具有可测量。因此，在教学中，教师要精心创设真实情境，组织学生开展丰富的度量活动，让他们充分经历度量的过程，从而体会度量对象的可测量。

例如，在“认识面积”的教学中，可以根据长方形的大小来说明面积的可测量。教师可以安排这样的度量活动：让学生分别以圆形、正三角形、小正方形、为测量工具，测量长方形的面积。即引导学生完整经历“先借助这些测量工具能否大致比较出长方形的面积的大小，再要准确反映长方形面积的大小，思考用什么测量工具（小正方形）作面积单位合适”的过程（如图1）。在这一过程中，教师带领学生充分体会面积的可测量，引导他们感悟：面积单位要密铺所测图形，且拼摆方便，正方形恰好具有這样的特点。

（二）度量对象具有唯一性

事物的属性是多元的，如橘子的形状、大小（直径、表面积、体积等）、颜色、质量、气味、甜度等都是它的属性。在这些属性中，有些可以通过度量、运算等数学的方式进行刻画。

对事物进行度量时，度量对象的唯一性体现在两个方面：一是只能在多种属性中锁定一种属性作为对象进行度量，二是度量对象的大小是唯一的。例如，在“认识面积”教学中，度量对象只指向面积这种属性，且每一个度量对象的面积大小是唯一的。虽然度量工具的不同会影响度量结果的精确性，但面积大小不会因为度量工具的不同而发生改变。

三、度量标准的优化

度量标准即度量单位，度量单位的形成会经历从多元到统一，从粗略到精细的发展过程。度量的基本方法就是将同一度量单位进行不断累加，同一属性的多个度量单位组合在一起就形成了度量工具。可见，对度量单位的认识与理解是发展量感的关键，教师应重视对度量单位形成过程的教学，让学生经历从“自主选择单位度量”到“使用统一单位度量”的过程。

（一）丰富材料：体验度量标准的多元

学生的度量方法具有多元性，度量单位就是把不同学生的度量方法标准化，从而确保度量结果的唯一性。教学中，教师要为学生提供丰富的学习材料，鼓励学生尝试以不同的度量标准作为度量工具开展度量活动，充分感受度量方法和度量工具的多样化。

例如，在“认识面积”的教学中，除了圆形、正三角形、小正方形、小长方形，等腰直角三角形、椭圆形、梯形等也可以用作度量标准。事实上，只要度量标准的面积比度量对象小，都可以用作度量标准来度量度量对象的面积。以此，可帮助学生积累丰富的度量经验，体会度量标准的多元性，感悟统一单位的必要性，深化对概念的理解与把握。

（二）改进策略：经历度量标准的优化

优化是数学重要的思想方法。教师要设计具有关联性、进阶性的驱动性任务，在具体度量活动中引导学生经历观察、操作，通过分析、比较各种度量标准在度量量的大小时的优势和不足，从建构、解构到重构，不断改进度量策略，选择最优策略进行度量，找到最优标准，完整经历度量标准优化的全过程。

例如，在“认识面积”教学中测量长方形的面积环节，可以设计“用不同形状的图形度量—用不同正方形密铺度量—用边长为1的正方形密铺度量”三个层次的度量活动，促使学生充分经历度量标准的优化过程，深化学生对度量单位意义的理解。

层次一：学生分别用圆、正三角形、正方形作为工具度量长方形的面积。探究发现：每个规则图形都可以作为度量标准，即长方形面积是由几个圆的面积组成，长方形面积是由几个正三角形的面积组成，长方形面积是由几个正方形的面积组成，其中正方形能铺满所测长方形。

层次二：学生用不同的正方形作为工具度量长方形的面积。探究发现：同一长方形可以由几种不同的正方形的面积组成，从而帮助学生理解统一度量单位的必要性。

层次三：学生分别用边长为1的正方形作为工具度量长方形的面积。探究发现：同一长方形可以由相同个数的边长为1的正方形的面积组成，且四条边一样长，在摆放时不用考虑方向和位置，作为面积单位更合适。

学生在教师的引导下，用不同形状和不同边长的图形作为度量标准对长方形面积进行度量，通过层层推进，在比较、辨析中得出结论：很多图形都可以用作度量标准进行度量，其中边长为1的小正方形是最合适、最方便的图形，度量的结果也是最准确的，为后面“面积单位”的教学打下基础。

四、度量活动的设计

丰富多彩的度量活动是发展学生量感的重要基础。教师可以创设多维度的度量活动，让学生循序渐进地形成对量的清晰表象，理解其度量本质。

（一）度量对象与标准单位的转化

度量对象的大小往往不等于一个度量单位的大小，因此，度量就是把度量对象的大小转化为若干个较小的度量单位的累加。度量时，需要选择最合适、较小的度量单位来测量度量对象的大小，本质上就是变大为小、用小量大。

例如，在“认识面积”的教学中，以小正方形面积为标准，用若干个小正方形来度量长方形面积的大小，本质上就是把度量对象（长方形的面积）转化为同一属性的较小的度量单位（小正方形的面积），用较小的度量单位的累加刻画度量对象的大小。

（二）具体测量到逻辑演算的渐跃

度量的进阶性体现在学生的度量活动，通常会经历三个阶段：第一阶段是用一个一个标准单位测量度量对象的大小，既指向量概念的理解，又指向量大小的度量，需要学生在真实情境中进行操作体验，在这个阶段，直接数标准单位数是主要的度量方式；第二阶段是用标准单位度量整体量的局部，根据整体量与局部量之间的关系，推演出整体量的大小，这个阶段需要将数局部单位数与演算整体单位数相结合；第三阶段是不借助具体的单位模型，通过想象、推理、归纳等思维活动，演算特定对象的大小，在这个阶段，基于逻辑的演算是主要的度量方式。

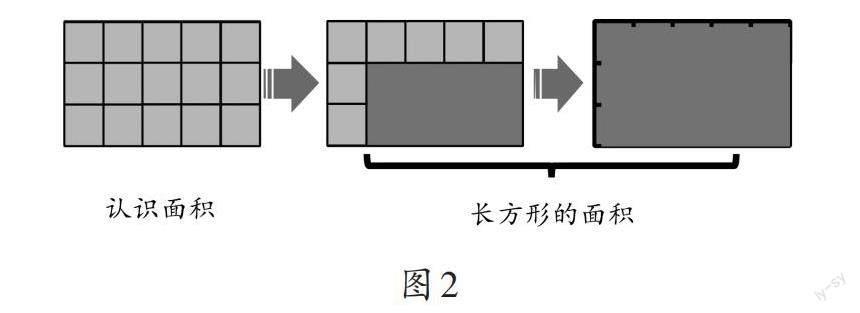
例如，人教版教材三年级下册“面积”单元是发展度量意识的重要内容，教学中，要让学生反复经历“摆—数”的活动过程，通过度量活动深化学生对面积概念的理解，理解面积的大小就是指度量对象包含了多少个面积单位，进而体会面积与面积单位之间的关系。在后续“长方形面积的计算”的教学中，需要借助面积与面积单位之间的关系，组织学生经历“用单位正方形密铺—用单位正方形部分铺—不用单位正方形想象铺”的逐步进阶过程（如图2），从而建立长方形的面积与长方形的长、宽之间的联系，理解“长×宽”代表了这个长方形包含的面积单位的个数，并归纳出长方形的面积计算公式：长方形的面积=长×宽。

五、度量结果的精确

在度量过程中，学生可以选择不同的度量标准对图形的面积进行度量，但是对于同一个度量对象，度量的结果是守恒的。当然，度量中必然存在误差，在给出度量结果的同时，也要理解其度量的误差范围。所谓度量结果的精确，也是指在允许误差范围内的精确。但误差有大有小，教师要引导学生思考误差产生的原因以及控制误差产生的策略，进而调整度量的结果，使其更加接近精确［6］。

（一）理解误差

误差是度量值与真实值之间的差异。度量活动的目的是得到精确的度量结果，需要运用科学的度量方法和精密的度量工具。但现实生活中没有绝对完美的度量操作，又因为度量工具的限制，再小的度量单位也无法满足更精细化的度量需求。因此，误差是绝对存在的。

（二）控制误差

虽然误差是不可避免的，但可以通过使用科学的度量方法和适切的度量工具来控制误差。例如，在“认识面积”的教学中，一是要使用科学的度量方法，在选用单位小正方形作为度量单位度量长方形的面积时，应尽量减小密铺的单位小正方形之间的缝隙，尽量不重叠、不超出度量对象的外边框等。二是要使用适切的度量工具，通过选用不同的图形（如圆形、正三角形、正方形）进行度量，发现选择正方形作为度量标准要比圆形、正三角形好，因为正方形平铺时没有缝隙，更接近于密铺，更接近长方形的真实面积。事实上，寻找适切的度量工具的过程就是对度量标准进行优化的过程。虽然在小学阶段并没有对度量提出精确性的要求，但是就在数学学习中培养坚持真理、严谨求实的科学态度的角度来讲，度量的精确性应该是度量学习的追求。

学生量感的培育并非一日之功，而是一个长期的、不断体验、循环反复的成长过程，是一个螺旋上升的过程。只有引导学生积极参加度量活动，在一次次度量活动中积累度量经验，才能逐步促进学生量感的发展。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［M］.北京：北京师范大学出版社，2022.

［2］孙思雨，孔企平.“量感”的内涵及培养策略［J］.小学数学教师，2021（7/8）：44-47.

［3］娜仁格日乐，史宁中.度量单位的本质及小学数学教学［J］.数学教育学报，2018，27（6）：13-16.

［4］邵光华，姜梦凡，苗榕峰.新课标视角下的量感及其培养［J］.课程·教材·教法，2023，43（5）：95-101.

［5］史宁中.为什么要强调量感［J］.小学教学（数学版），2021（10）：8-10.

［6］平国强.“量感”及其培养［J］.教学月刊·小學版（数学），2023（1/2）：27-31.

（浙江省杭州大关小学教育集团）