基于学情分析的精准教学实践<br/>——以“百分数的概念建构”的教学为例

基于学情分析的精准教学实践
——以“百分数的概念建构”的教学为例

2024-03-15江苏省南京市科睿小学仇学春

小学教学研究 2024年1期

江苏省南京市科睿小学仇学春

江苏省南京市琅琊路小学张冬梅

“百分数”是小学数学传统的教学内容，百分数源于分数，源自分数的“率”，表示两个数或数量的倍数关系。过去的课程标准一般把百分数作为“数与代数”领域的重要内容。《义务教育数学课程标准（2011 年版）》在第二学段“数的认识”部分要求“理解小数和分数的意义，理解百分数的意义”，并在案例部分说明“百分数是同分母（统一标准）的比值，便于比较。希望学生能够理解它们的含义，在生活中能够合理使用” 。《义务教育数学课程标准（2022 年版）》则将百分数作为“统计与概率”领域的内容，要求“结合具体情境，探索百分数的意义，能解决与百分数有关的简单实际问题，感受百分数的统计意义”。具体地说，要引导学生“知道百分数是两个数量倍数关系的表达，既可以表达确定的数据，如饮料中果汁的含量、税率、利息和折扣等，也可以表达随机的数据，如某篮球运动员罚球命中率、某城市雾霾天数所占比例等”。这样的改变丰富了百分数概念的内涵，将百分数作为一个重要的统计特征量加以认识，突出了其统计意义。

一、学情调查

在教学百分数的意义之前，为了了解学校六年级学生有关百分数意义的“前概念”，精准实施教学，笔者结合学生可能的数学经验设计了以下三个问题，对学校200 名学生进行了调查。调查采取书面答题的形式，学生在20 分钟内独立完成后上交。

1.下面信息中的数叫作百分数。对于这些百分数，你是怎样理解的？（可以画图、举例说明）

（1）六（2）班男生人数占全班人数的45%。

（2）今年全市空气质量为优的天数比去年增加了12%。

2.调查发现，五年级有15%的同学近视，六年级有12%的同学近视。小亮认为，五年级近视的同学一定比六年级近视的同学多。对此，你有什么看法？

3.六（2）班的王恒和张兵是足球爱好者，有一天他们练习踢点球，王恒的命中率是80%，张兵是75%。谁点球踢得好？如果再比一次，还一定是王恒踢得好吗？

第1 题侧重了解学生对百分数表示确定数据倍数关系的理解，第2 题侧重了解学生对百分数表示的百分率的认识，第3 题侧重了解学生对百分数表示随机数据关系的理解，分析学生的随机意识。

二、调查结果及分析

为了更深入地了解学生的“前概念”，笔者对调查结果进行了细致的分析，尝试从学生关于百分数认识的已有基础、认知水平和发展可能性三个维度进行。“已有基础”侧重了解学生关于百分数的知识经验和生活经验，“认知水平”侧重了解学生“前概念”的理解层次及表征方式，“发展可能性”侧重了解学生百分数概念的素养表现及发展水平，笔者将其形成了“三维度六方面”学情分析框架（如图1）。

图1

（一）学生有关百分数概念的已有基础

学生已经有了分数学习的经验，对百分数意义的理解有了一定的认知基础，同时在日常生活中他们或多或少也了解了一些百分率。第1 题的调查结果表明：所有学生都能准确理解并表征“六（2）班男生人数占全班人数的45%”的含义，但是在表征百分数意义的方式上有些区别，67%的学生能用不同的图形来表示并能准确地加以解释，25.5%的学生习惯用文字表示，有7.5%的学生则习惯用算式表示。在用图形表征的学生中，有32.8%的学生选择用圆形图表示，24.6%的学生选择用线段图表示，42.6%的学生选择用矩形图表示。

值得注意的是，只有约66.7%的学生能够较准确地理解“今年全市空气质量为优的天数比去年增加了12%”的含义。

百分数的本质是表示一个比率，每个百分数所表示的具体数量既和它本身的大小有关，也和它整体的数量有关。第2 题的调查结果：20.5%的学生认为，15%＞12%，所以五年级近视的人数一定比六年级的多；79.5%的学生认为“不一定，因为两个年级的人数不知道”，其中有学生能够借助举例来说明具体的数量多少。

第3 题的调查结果：66.7%的学生认为一定是王恒踢得好，理由是80%＞75%；33.3%的学生认为不一定，理由是再踢一次不一定是王恒踢得好。

（二）学生有关百分数概念的表征水平

对于第1 题的第（2）小题用百分数表示一个量和另一个量的倍数关系，学生的认知水平表现出了明显的区别，于是笔者又进一步分析学生对于这一情境中百分数所表示意义的表征水平层次。具体结果如表1 所示。

表1 学生对百分数表示一个量和另一个量的倍数关系的表征水平层次结果

表2 六年级男生1 分钟跳绳情况统计表

水平一：不能理解这里的百分数表示的是对两个量进行比较的结果。这部分学生只表示出去年的12%，未能清楚地表征“今年比去年增加的部分”与去年比较的关系（如图2）。

图2

水平二：仅能理解这里的百分数表示的是对两个量比较的结果。这部分学生知道12%是今年比去年增加的，但未能表征增加的12%的单位“1”是去年的（如图3）。

水平三：能理解这里的百分数表示的是对两个量比较的结果并能准确表征，有的学生对“12%”的单位“1”给出了更加准确的解释（如图4）。

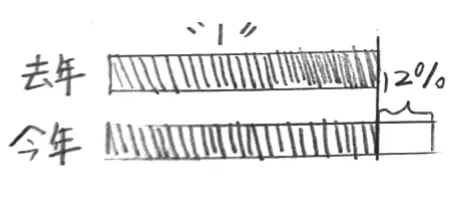
图4

（三）学生的素养发展的现状与可能分析

百分数不仅可以表示确定数据的倍数关系，还可以表示随机数据的倍数关系。因此，这一内容对于学生核心素养的发展主要表现在数学意识方面。而对百分数意义的理解也必然会应用图形表征，因而有利于发展学生的几何直观。同时，百分数在实际生活中应用广泛，因而有利于发展学生的应用意识。从调查结果来看，66.7%的学生的随机意识的发展还比较薄弱，38%的学生在借助图形表征一个量是另一个量的百分之几时仍感到困难，数的意义理解与形的结合能力还有待发展。从调查涉及的实际问题来看，还有33%左右的学生对实际问题中的百分数的应用理解感到困难，应用意识有待增强。

三、精准实施教学

基于上述对学校六年级学生认识百分数的学情分析，教师更清晰地把握了学生认识百分数的“前概念”，这为教师从已有的知识经验、思维水平和素养发展等方面引导学生整体建构百分数的意义，实施精准教学提供了很多有益的启示。

（一）会说话的“百分数”

调查结果表明，学生对于理解部分量占总量的百分数意义比较简单，但是对于理解两个相关量的百分比还有一定的难度。因此，教师在教学时要关注百分数意义的抽象概括过程，引导学生真正理解百分数的意义，同时要关注用百分数表示一个数比另一个数多（或少）百分之几的意义的理解，体会“百分数”会说话。

（1）谈话：百分数在生活中有着广泛的应用，教师也带来了几个百分数（如图5），你知道这些百分数表示的意思吗？请同学们按照任务单上的内容独立思考探究，完成后小组内合作交流。

图5

（2）组织学生汇报交流。

生1：男生人数和全班人数比较，把全班人数看作单位“1”，平均分成100 份，男生人数有这样的40 份。

生2：九月份用水量和八月份用水量比较，把八月份用水量看作单位“1”，平均分成100 份，九月份用水量有这样的95.5 份。

生3：今年比去年增加空气质量为优的天数与去年的比较，把去年空气质量为优的天数看作单位“1”，平均分成100 份，增加的空气质量为优的天数有这样的12 份。

师：这里哪个百分数比较特殊？

生：95.5%比较特殊，它的分子是一个小数。

（3）抽象概括百分数的意义。

师：什么是百分数？你们能用自己的方式表示百分数和分数之间的联系吗？

生1：百分数表示一个数是另一个数的百分之几。

生2：百分数的分母是100，分母是100 的分数不一定是百分数。

（4）理解百分比。

师：根据六（2）班男生人数占全班人数的40%，你能联想到什么知识？

生1：老师，我想到了女生人数占全班人数的60%。

生2：我发现了女生人数与男生人数的比是3∶2。

生4：还可以这样说，男生人数是女生人数的

师：百分数和分数、比、除法这些学过的知识是相互联系的（如图6），都可以表示两个量之间的倍数关系。所以百分数又叫百分比。

图6

（5）体会百分数表示的具体数量与单位“1”有关。

师：学校绘画组男生占总数的10%，学校书法组男生占总数的12%，哪个组的男生多？

生1：因为12%大于10%，所以书法组的男生多。

生2：无法确定，因为不知道两个组的人数。

师：这里的百分数表示的大小与什么有关？

生：既与单位“1”有关，还与本身的大小有关。

（二）调皮的“命中率”

调查结果表明，66.7%的学生的随机意识的发展还比较薄弱，他们对于百分数可以表示随机数据的倍数关系的认识还比较模糊。因此在教学时，教师应帮助学生强化对“命中率”意义的理解，引导学生体会“命中率”是通过抽样或调查得到的，如果用一次抽样或调查的结果来分析、判断，所得到的结论不能“百分之百”地成立，要考虑数据本身的“随机性”。当然，还可以让学生在具体情境中自己确定标准，体会百分数的统计意义，增强数据的随机意识。

（1）出示任务：（如图7）