作业车间调度的多工序精确联动邻域结构混合进化算法
2024-03-13巴智勇袁逸萍裴国庆
巴智勇,袁逸萍,裴国庆,王 波
(1.新疆大学 机械工程学院,新疆 乌鲁木齐 830017;2.卓郎新疆智能机械有限公司,新疆 乌鲁木齐 830057)
0 引言
作业车间调度问题(Job Shop Scheduling Problem, JSP)不仅是典型的NP-hard问题,还是管理领域中许多优化问题的通用模型,如项目计划调度、岸桥调度优化[3]、轨道列车时刻表调度优化[4]等。另外,JSP模型能以一种明确的方式对问题添加各种侧约束和目标,使其应用范围不限于调度优化问题[5]。
学者们针对JSP提出了大量高效的求解方法,如数学规划[6]、调度规则[7]、启发式和元启发式算法。由于JSP的NP-hard特性,精确求解方法只适合求解小规模问题,难以应用于实际生产,当前主流研究方向是采用近似方法求解JSP。近似求解方法包括大量经典和新型的元启发式方法,如粒子群优化[8]、遗传算法[9]、差分进化[10]、蚁群算法[11]、细菌觅食算法[12]、教与学优化算法[13]和灰狼优化算法[14]等。然而,受限于基本理论和算法框架,单一的元启发式算法在JSP上的求解效果并不理想,越来越多学者利用两个或多个算法的互补特征开发更为先进的混合算法。REN等[15]提出一种混合局部搜索策略的遗传算法求解JSP,通过引入多样化的种群更新机制防止算法过早收敛;REHAB等[16]设计了基于邻域多样化强化策略的粒子群优化算法,实现了对JSP解空间的广泛搜索;PENG等[17]提出基于路径重连的禁忌算法,采用路径重连方法产生更多样的候选解,同时在禁忌搜索中应用更复杂的N7邻域,改进了多个JSP基准算例的上界;CHENG等[5]提出一种基于机器最长公共子序列的新型交叉算子,并设计基于质量与相似性的种群替代策略来保持种群多样性,更新了多个JSP基准算例的已知最优解;LIANG等[18]提出一种基于新型邻域结构的自适应遗传算法求解JSP,该算法的交叉概率和变异概率可以根据种群适应度的离散程度进行非线性和自适应调整,实验结果表明算法在求解精度和收敛效率方面均有显著提升;ALKHATEEB等[19]设计了一种集成模拟退火搜索的混合离散布谷鸟算法求解JSP,该算法首先采用基于对抗学习的方法生成多样性的初始解,通过集成变邻域搜索与莱维飞行方法实现广泛的局部搜索,并设计了基于精英对抗的学习方法跳出局部最优解;SHAHED等[20]提出性能驱动的元启发式切换方法求解JSP,该方法将多算子差分进化和粒子群优化集成在单一算法框架中,并引入性能驱动的切换机制将搜索性能不佳的算法切换为其他可能的算法。
大多数先进的JSP混合算法通过局部搜索组件来强化对有潜力解空间的深度搜索,而邻域结构作为局部搜索的核心,极大地影响着算法的效率和质量。JSP局部搜索中较为常用的是基于关键路径的工序块邻域结构,通过交换关键工序块中任意两工序可以形成新解。当前研究者大多从减少邻域结构的规模和保证可行邻域移动两方面构建有效的邻域结构。VAN LAARHOVEN等[25]交换同一台机器上相邻关键工序的邻域结构,记作N1,然而N1邻域结构不但规模大,而且包含大量非改进的移动操作;GRABOWSKI等[26]首先提出块的概念,并将邻域结构定义为把一个内部关键工序插入其块首之前或块尾之后的一种机制。此后,NOWICKI等[27]、BALAS等[28]和ZHANG等[29]提出更具竞争力的N4,N5,N6,N7邻域结构;赵诗奎等[30-32]通过分析机器上空闲时间的利用机理,扩大了关键工序的移动范围,并在此基础上进一步提出多工序联动邻域结构和近似评价方法。
本文结合JSP的特性,设计了一种3对工序精确联动的邻域结构。针对进化算法中存在的种群早熟现象,设计了基于邻域惩罚的交叉父本配对选择算子与基于动态惩罚阈值的种群更新策略,并将基于新型邻域结构的禁忌搜索嵌入进化算法框架,设计了兼具全局与局部搜索能力的JSP求解算法。最后,将本文所提算法与其他先进算法在基准算例上进行对比分析,验证了所提算法的有效性。
1 问题描述
JSP问题可描述为:n个工件J={J1,J2,…,Jn}在m台机器M={M1,M2,…,Mn}上加工,每个工件Ji由m个连续工序{Oi,1,Oi,2,…,Oi,m}组成,相应的加工机器集合为{σi,1,σi,2,…,σi,m},工序Oi,j在机器σi,j上的加工时间为pti,j,以最小化最大完工时间(Cmax)为优化目标。
对JSP问题作以下假设:
(1)所有工件零时刻达到,所有机器零时刻可用。
(2)同一工件同一时刻最多只能在一台机器上加工,一台机器同一时刻最多只能加工一个工件。
(3)工序在机器上一旦开始加工就不能中断。
(4)工序之间的运输时间和生产准备时间都包含在加工时间中。
以最小化最大完工时间为优化目标建立JSP混合整数规划模型,模型构建过程中涉及的参数符号及说明如下:
sti,j为工序Oi,j的开工时间;
eti,j为工序Oi,j的完工时间;
JSP混合整数规划模型为:
min(Cmax)=min(max(eti,j)),∀Oi,j;
(1)
sti,j≥sti,j-1+pti,j-1,∀{Oi,j,Oi,j-1};
(2)
eti,j=sti,j+pti,j,∀Oi,j;
(3)
(sti,j-etr,s)yr,s,i,j(1-yi,j,r,s)+(str,s-eti,j)·
yi,j,r,s(1-yr,s,i,j)≥0,∀{Oi,j,Or,s};
(4)
yi,j,r,s+yr,s,i,j=0;
(5)
sti,j≥0。
(6)
其中:式(1)为目标函数;式(2)为同一工件的紧邻工序的顺序约束;式(3)为计算工序的完工时间;式(4)与式(5)定义了同一机器上紧邻两道工序的加工时间不能重叠,即同一台机器上后加工工序的开始时间不能早于前一道工序的完工时间;式(6)定义了工序开工时间的非负性。
2 多工序精确联动的邻域结构
邻域结构的本质在于如何引导关键工序更充分地利用机器空闲时间,作为最有效的邻域结构之一,N7邻域结构虽然通过在较大范围内移动单个关键工序对原方案产生较强扰动来生成邻域解[33],但因缺乏足够的理论分析,可能会产生大量无效的移动操作。为此,本文对N7邻域结构进行理论分析,提出关键工序无效移动的条件并进行证明,进而对N7邻域结构进行扩展优化。相关符号说明如表1所示。
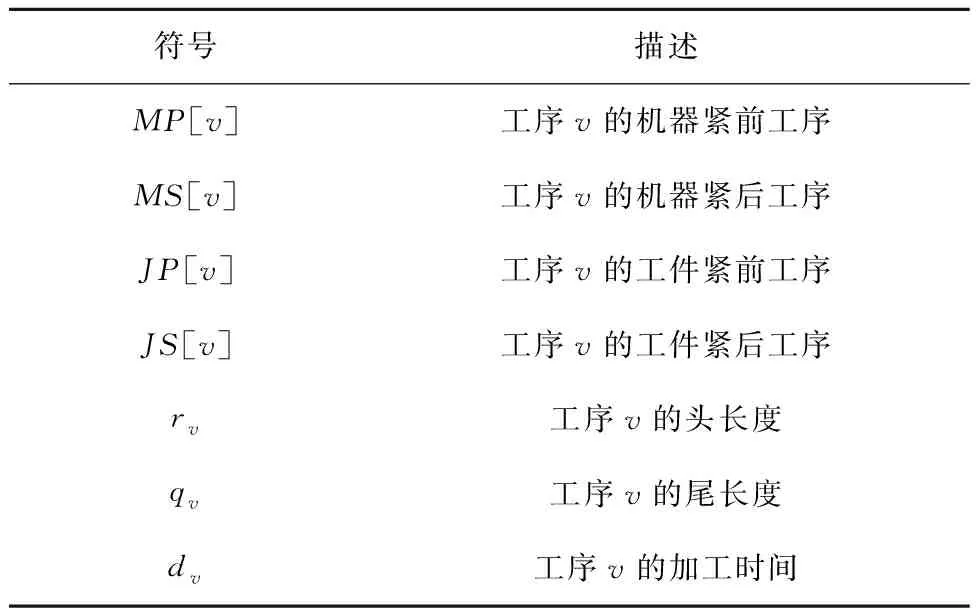
表1 符号表示及其说明
2.1 N7邻域无效移动的理论分析
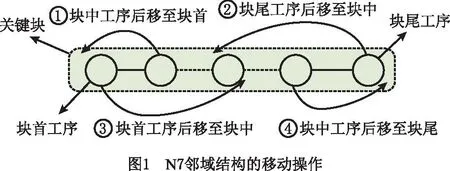
N7邻域结构存在4类关键工序移动操作,如图1所示,当工序移动后,采用近似求解[34]方法重新计算受影响工序新的头尾长度,则邻域解的近似值C′max为受影响工序的头尾长度之和的最大值,若C′max大于原方案的最大完工时间Cmax,则可证明该工序移动是无效的。
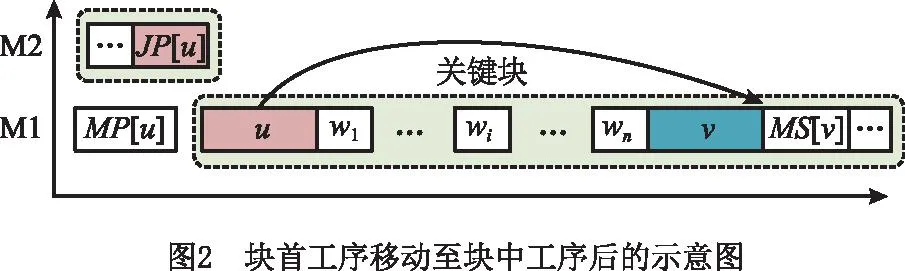
定理1关键块中存在两个工序u和v,分别为块首与块中工序,对于u与MS[v]之间的任意工序wi,若rJP[wi]+dJP[wi]+du≥rwi,则工序u移动到工序v之后不会减少最大完工时间。
证明如图2所示,将工序u移动至v后,得到受影响工序{w1,…,wi,…,wn,v,u},采用近似评估方法重新计算各受影响工序的头尾长度和C′max,计算如下:
(7)
C′max=max{r′w1+q′w1,…,r′wi+q′wi,…,
r′wn+q′wn,r′v+q′v,r′u+q′u}。
(8)
移动前,从工序wi角度,
Cmax=rwi+dwi+…+dwn+dv+qMS[v]。
(9)
移动后,工序MP[u]与v之间的工序将直接或间接利用块前原有机器空闲时间以及u移动后产生的新的机器空闲时间,从工序wi的角度,近似最大完工时间C′max(wi)=r′wi+q′wi,由式(7)递推可得:
r′wi≥rJP[wi]+dJP[wi];
(10)
q′wi≥qMS[v]+du+dv+dwn+…+dwi。
(11)
整理式(10)和式(11)可得
C′max(wi)≥rJP[wi]+dJP[wi]+du+dv+dwi+…
+dwn+qMS[v]。
(12)
若rJP[wi]+dJP[wi]+du≥rwi成立,则必有
C′max(wi)≥
rwi+dwi+…+dwn+dv+qMS[v]。
(13)
与式(9)相比,有C′max(wi)≥Cmax,则C′max≥Cmax必成立。证毕。
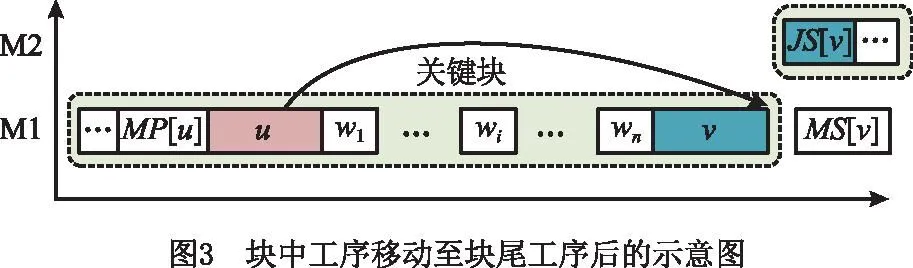
定理2关键块中存在两个工序u和v,分别为块中与块尾工序,若qJS[u]≥qJS[v],则工序u移动到v之后不会减少最大完工时间。
证明如图3所示,移动后,从工序u的角度,近似最大完工时间C′max(u)=r′u+q′u,由式(7)递推可得:
r′u≥rMP[u]+dMP[u]+dw1+…+dwn+dv;
(14)
q′u≥qJS[u]+du。
(15)
整理式(14)和式(15)可得C′max(u)≥rMP[u]+dMP[u]+du+dw1+…+dwn+dv+qJS[u],若qJS[u]≥qJS[v]成立,则
C′max(u)≥rMP[u]+dMP[u]+du+dw1+…
+dwn+dv+qJS[v]=Cmax,
(16)
C′max≥Cmax必成立。证毕。
定理3关键块中存在两个工序u和v,为块首与块尾工序,若rJP[wi]+dJP[wi]+du≥rwi且qJS[v]≤qJS[u],则工序u移动到v之后不会减少最大完工时间。
证明如图4所示,移动后,从工序u的角度,近似最大完工时间C′max(u)=r′u+q′u,由式(7)递推可得
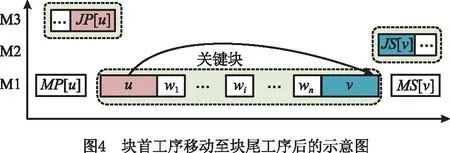
r′u≥rJP[wi]+dJP[wi]+dwi+…+dwn+dv。
(17)
当rJP[wi]+dJP[wi]+du≥rwi成立时,由式(17)可得
r′u≥rwi+(dwi+…+dwn+dv)-du
=rv+dv-du。
(18)
由式(7)推得q′u≥qJS[u]+du必成立,结合式(18)可得C′max(u)≥rv+dv+qJS[u],若qJS[v]≤qJS[u],则C′max(u)≥rv+dv+qJS[v]>Cmax,有C′max≥Cmax必成立。证毕。
定理4关键块中存在两个工序u和v,分别为块中与块尾工序,对于u与MS[v]之间的任意工序wi,若qJS[wi]+dv≥qwi-dwi,则工序v移动到u之前不会减少最大完工时间。
证明如图5所示,将工序v移动到u之前,得到受影响工序{v,u,w1,…,wi,…,wn},各自近似头尾长度计算如下:
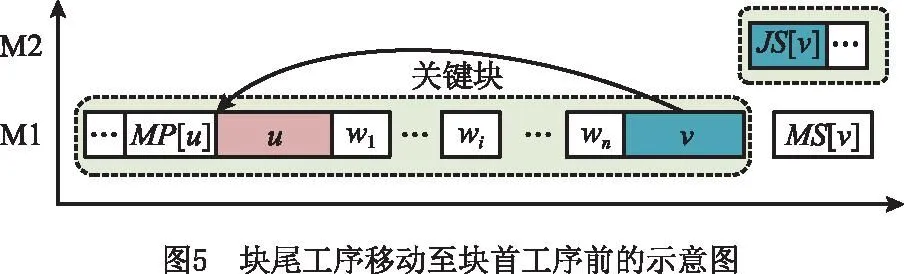
(19)
从工序wi的角度来看,移动后的最大完工时间C′max(wi)=r′wi+q′wi。由式(19)推导得到工序wi的近似头尾长度:
r′wi≥qMP[u]+dMP[u]+dv+du+dw1+…
+dwi-1=rwi+dv;
(20)
q′wi≥qJS[wi]+dwi。
(21)
结合式(20)和式(21)可得C′max(wi)≥rwi+dv+qJS[wi]+dwi,若qJS[wi]+dv≥qwi-dwi成立,则C′max(wi)≥rwi+(qwi-dwi)+dwi=rwi+qwi=Cmax必成立,进一步可得C′max≥Cmax。证毕。
定理5关键块中存在两个工序u和v,分别为块首与块中工序,若rJP[v]+dJP[v]≥ru,则将工序v移动到工序u之前不会减少最大完工时间。
证明如图6所示,从工序v的角度,移动后的近似最大完工时间C′max(v)=r′v+q′v,由式(19)推导可得:
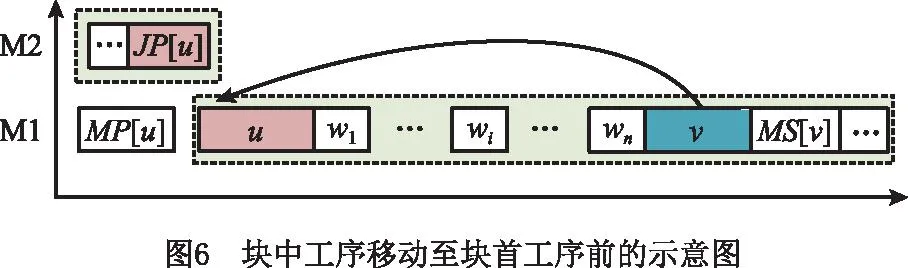
r′v≥rJP[v]+dJP[v];
(22)
q′v≥qMS[v]+dwn+…+dw1+du+dv。
(23)
当rJP[v]+dJP[v]≥ru成立时,结合式(22)和式(23)可得C′max(v)≥ru+du+dw1+…+dwn+dv+qMS[v]=Cmax,进一步可得C′max≥Cmax。证毕。
定理6关键块中存在两个工序u和v,分别为块首与块尾工序,对于MP[u]与v之间的任意工序wi,如果qJS[wi]+dv≥qwi-dwi且rJP[v]+dJP[v]≥ru,则将工序v移动至工序u之前不会减少Cmax。
证明如图7所示,移动后,从工序v的角度,近似最大完工时间C′max(v)=r′v+q′v,由式(19)推导得
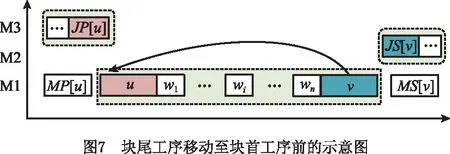
q′v≥qJS[wi]+(dwi+…+dw1+du)+dv。
(24)
若qJS[wi]+dv≥qwi-dwi成立,则q′v≥qwi+(dwi-1+…+dw1+du)=qu必成立。由式(19)推导得r′v≥rJP[v]+dJP[v],若rJP[v]+dJP[v]≥ru成立,则r′v≥ru必成立。由以上结果可得C′max(v)≥ru+qu=Cmax必成立,进一步可得C′max≥Cmax。证毕。
可见,N7邻域结构中参与移动的工序数量多且移动范围广,能从多个角度利用机器空闲时间,但也存在不能减少Cmax的无效移动操作。以上基础理论分析为识别N7邻域结构中的无效移动操作提供了理论支撑,同时也为更加复杂的多工序联动邻域结构设计指明了方向。
2.2 多工序精确联动邻域
本文将文献[32]提出的多工序联动的触发条件与N7邻域无效移动判定条件结合,构建更为强化的邻域结构PN7+2MT,具体实现如下:
情形1块首工序u移动至块尾工序v后,联动工序的移动方式如图8所示,具体步骤如下:
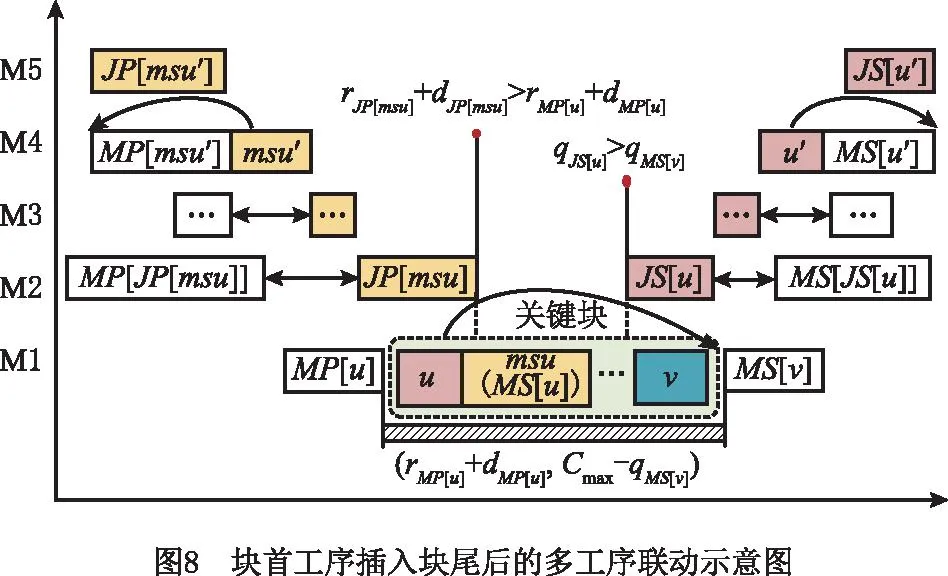
(1)令msu=MS[u],如果JP[msu]≠∅,且满足rJP[msu]+dJP[msu]>rMP[u]+dMP[u],则按照工序的最早完工时间查找工序msu的某一道工件前序工序msu′,如果存在工序msu′满足条件MP[msu′]≠∅,且rMP[msu′]+dMP[msu′]=r′msu,则交换工序MP[msu′]和msu′。
(2)如果JS[u]≠∅,且满足qJS[u]>qMS[v],则按照工序的最晚开工时间查找工序u的工件维某一道后序工序u′,如果存在工序u′满足条件MS[u′]≠∅,且q′u-d′u=qMS[u′],则交换工序u′和MS[u′]。
情形2块首工序u移动到块中工序v之后,联动工序的移动方式如图9所示,具体步骤如下:
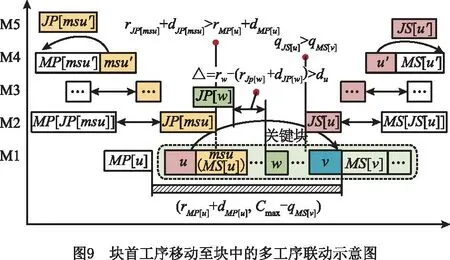
(1)令msu=MS[u],如果JP[msu]≠∅,且满足rJP[msu]+dJP[msu]>rMP[u]+dMP[u],则按照工序的最早完工时间查找工序msu的某一道工件前序工序msu′,如果存在工序msu′满足条件MP[msu′]≠∅,且rMP[msu′]+dMP[msu′]=r′msu,则交换工序MP[msu′]和msu′。
(2)若MS[u]与MS[v]之间的任意工序w均满足rJP[w]+dJP[w]+du
情形3块中工序u后移到块尾工序v之后,联动工序的移动方式如图10所示,具体步骤如下:
(1)令msu=MS[u],如果JP[msu]≠∅,且满足rJP[msu]+dJP[msu]>ru,则按照工序的最早完工时间查找工序msu的某一道工件前序工序msu′,如果工序msu′满足条件MP[msu′]≠∅,且rMP[msu′]+dMP[msu′]=r′msu,则交换工序MP[msu′]和msu′。
(2)如果JS[u]≠∅,且满足qJS[u]>qMS[v],则按照工序的最晚开工时间查找工序u的某一道工件的后序工序u′,如果存在工序u′满足条件MS[u′]≠∅,且qu′-du′=qMS[u′],则交换工序u′和MS[u′]。
情形4块尾工序v移动到块首工序u之前,联动工序的移动方式如图11所示,具体步骤如下:
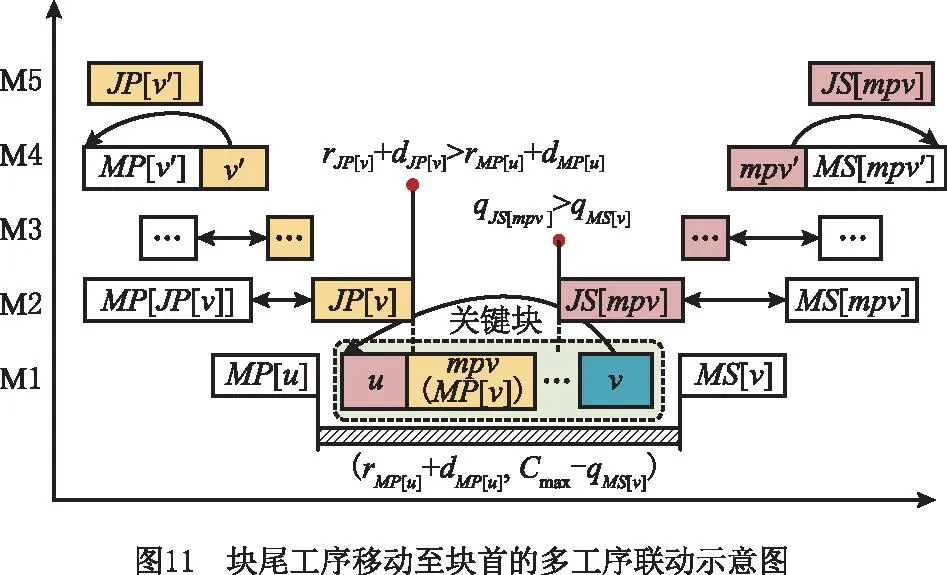
(1)令mpv=MP[v],如果JS[u]≠∅,且满足qJS[mpv]>qMS[v],则按照工序的最晚开工时间查找工序mpv的某一道工件后序工序mpv′,如果存在工序mpv′满足条件MS[mpv′]≠∅,且qmpv′-dmpv=qMS[mpv′],则交换工序mpv′和MS[mpv′]。
(2)如果JP[v]存在,且满足rJP[v]+dJP[v]>rMP[u]+dMP[u],则按照工序的最早完工时间查找工序v的某一道工件前序工序v′,如果存在工序v′满足条件MP[v′]≠∅,且rMP[v′]+dMP[v′]=r′v,则交换工序MP[v′]和v′。
情形5块尾工序v移动到块中工序u之前,联动工序的移动方式如图12所示,具体步骤如下:
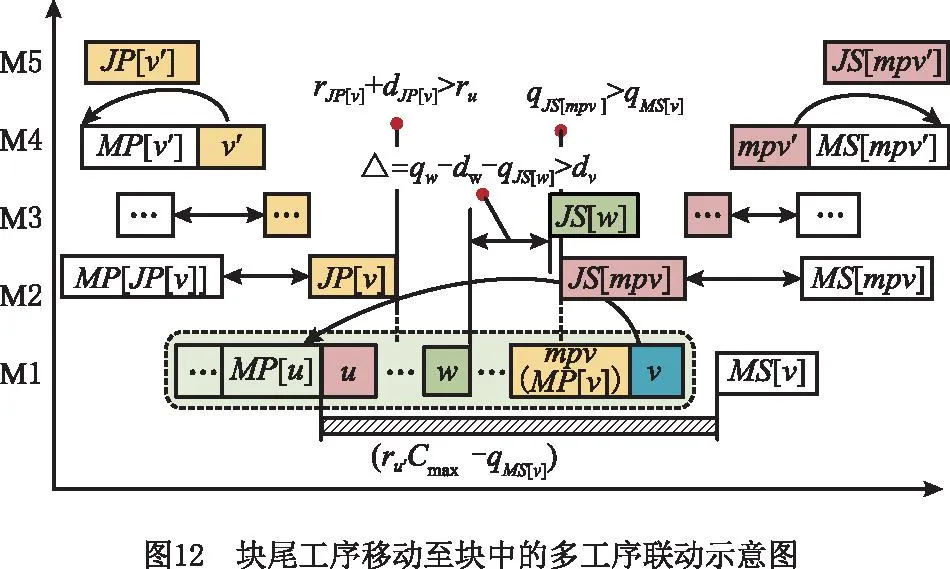
(1)令mpv=MP[v],如果JS[u]≠∅,且满足qJS[mpv]>qMS[v],则按照工序的最晚开工时间查找工序mpv的某一道工件的后序工序mpv′,如果存在工序mpv′满足条件MS[mpv′]≠∅,且qmpv′-dmpv=qMS[mpv′],则交换工序mpv′和MS[mpv′]。
(2)对于MP[u]与v之间的任意工序w满足qJS[w]+dv
情景6块中工序v移动到块首u之前,联动工序的移动方式如图13所示,具体步骤如下:

(1)令mpv=MP[v],如果JS[u]≠∅,且满足qJS[mpv]>qMS[v],则按照工序的最晚开工时间查找工序mpv的某一道工件的后序工序mpv′,如果存在工序mpv′满足条件MS[mpv′]≠∅,且qmpv′-dmpv=qMS[mpv′],则交换工序mpv′和MS[mpv′]。
(2)如果JP[v]存在,且满足rJP[v]+dJP[v]>rMP[u]+dMP[u],则按照工序的最早完工时间查找工序v的某一道工件的前序工序v′,如果存在工序v′满足条件MP[v′]≠∅,且rMP[v′]+dMP[v′]=r′v,则交换工序MP[v′]和v′。
2.3 邻域结构复杂度分析
对于n个工件m台机器的JSP,根据N7邻域结构的4类移动方式,当工序块有n个工序时,总的交换次数最多,为(n-1)×4×m,其计算复杂度为O(nm)。对于PN7+2MT,在N7邻域结构的基础上查找另外两对交换工序,两次交换的最大查找次数为2×(m-1),同时因为块首工序后移与块尾工序前移产生的联动工序交换只需计算一次,所以PN7+2MT的最多查找次数为(n-1)×2×m×2×(m-1)+(n-1)×2×m+2×m×2×(m-1),计算复杂度为O(nm2)。
3 算法设计
3.1 算法框架
进化算法不但具有良好的理论研究基础,而且在工程领域应用广泛。然而进化算法偏重全局搜索,需要与基于问题特征的局部搜索集成才能获得高质量的解。禁忌搜索算法侧重于局部搜索,可以很好地结合JSP特征信息的邻域结构,引导算法进行有效搜索。为了将全局搜索和局部搜索相结合,本文提出一种基于多工序精确联动邻域结构的混合进化算法(Hybrid Evolutionary Algorithm with Multi-operation precise joint movement Neighborhood Structure,HEA-MNS)。在进化算法部分引入基于新型个体距离的配对选择算子,防止近亲繁殖;然后,采用基于动态惩罚阈值的种群更新机制构建下一代种群,通过动态调整惩罚阈值实现集中性与多样性搜索的动态平衡。禁忌搜索采用多工序联动邻域结构PN7+2MT对大邻域空间进行精确搜索,提高了HEA-MNS的局部搜索能力。
算法1为HEA-MNS的基本框架,算法首先从一个初始随机种群开始,采用禁忌搜索优化每个染色体(4行~6行);然后,采用配对选择算子选择交叉父本,通过交叉算子生成新的子代染色体(8行~9行);再次,采用禁忌搜索对新生成的子代染色体进行优化(10行~11行);最后,采用种群更新算子从原种群与子代染色体的集合中选择下一代种群(12行)。下面详细介绍HEA-MNS的主要组件。
算法1HEA-MNS伪代码。
1 输入:J,M,D。
2 输出:算法终止时的最优调度方案s*与完工期Cmax。
3 初始化种群P={s1,…,sp}
4 For i={1,…,p} do
5 si←Tabu_Search(si)
6 end for
7 While终止条件未满足do
8 (sj,sk)= Select_Parents(P)
9 (sp+1,sp+2)←Crossover(sj,sk)
10 sp+1← Tabu_Search(sp+1)
11 sp+2← Tabu_Search(sp+2)
12 {s1,…,sp}←Population_Updating(s1,…,sp,sp+1,sp+2)
13 end while
14 s*=argmim{f(si)|i=1,…,p}
15 Return s*
3.2 编码与解码
本文采用文献[35]的编码方法,即一条染色体由m个基因串组成,每个基因串表示各工件在机器上的加工序列,基因串的工序基因用相应的工件序号表示,因此染色体的长度为n×m。
对于JSP,以最大完工时间为优化目标的最优调度必在主动调度集合中[36],因此本文选择GONG等[37]提出的插入式贪婪主动解码算法。
3.3 禁忌搜索
作为车间调度问题最有效的求解方法之一,禁忌搜索能够有效引导算法深入搜索有潜力的区域,为了加强局部搜索的扰动强度和有效性,本文采用第2章提出的精确多工序联动邻域结构PN7+2MT生成邻域解。
(1)移动评估 当一组可行邻域解被构造出来后,每个邻域解都需要被重新计算或评估其最大完工时间,本文采用赵诗奎等[32]提出的快速评估方法对邻域解进行近似计算。
(2)禁忌表 禁忌表作为禁忌搜索的短期记忆,可以有效避免搜索过程出现死循环。算法采用与TSSA(tabu search and simulatecl annealing)算法[38]相同的禁忌表结构。具体来说,如果一次移动包含交换工序u和v,则u和v之间的所有工序及其位置都存储在禁忌表中。禁忌表长度根据决策变量规模动态调整[38],即在两个给定的极值[Lmin,Lmax]之间随机选取。
(3)邻域解选择 在每次迭代中,禁忌搜索过程首先考虑不在禁忌表中的移动,并从中选择产生最优目标值的邻域解。若两种或两种以上的移动都具有相同的最优目标值,则从中随机选择一个移动;如果一个移动能够带来比当前最优解更好的解,且该移动在禁忌表中,则对该移动进行特赦。
(4)终止准则 当找到最优解或禁忌搜索的连续未改善迭代次数超过给定极限值时,禁忌搜索过程停止。
3.4 基于邻域惩罚的配对选择与交叉操作
在进化算法中,配对选择操作的主要任务是从父代种群中选择用于生成子代个体的配对父本,其选择标准在很大程度上影响算法的收敛性与多样性。为了增强算法产生多样化后代的能力,本文提出基于邻域惩罚的配对选择操作,其基本思想为:算法随机从父代种群中选取一个染色体,另一个染色体从其惩罚邻域外随机选择,如果惩罚邻域外无其他染色体,则从惩罚邻域内选择距离最远的一个染色体。为方便后续论述,本文给出以下定义:
定义1两个解之间的距离。对于给定的两个解x=(x1,…,xi,…,xm)和y=(y1,…,yi…,ym),解x与y的距离为各机器上工序排列的偏差距离的总和,记作Dpos(x,y),
Dpos(x,y)=
(25)
式中:n和m分别为工件数量与机器数量;xi和yi分别为解x与y的第i机器上的工序序列;pos(a,b[])为a在b序列中的位置。
定义2解与种群的距离。对于给定的种群P={s1,…,sp}与一个解I,I与种群P的距离为I与种群P中所有个体距离的最小值,记为DCI(I,P),
DCI(I,P)=min{Dpos(I,sj)|sj∈P}。
(26)
定义3种群的密度。对于给定的种群P={s1,…,sp},种群P的密度为种群的各个解si相对于P{si}距离的平均值,记作DCIav(P),
(27)
算法2中给出了交叉算子的伪代码,对于当前种群P={s1,…,sp},采用以下规则选取交叉父本{sj,sk}。首先,根据当前种群的密度设定父本选择的惩罚距离D,并初始化候选集合Candidate与惩罚集Penalized(3行),从当前种群Candidate中随机选择一个染色体作为第1个父本sj,将其从Candidate删除(4行~5行);然后,通过不断迭代,将与父本sj距离小于D的染色体从Candidate删除,并添加至Penalized中(6行~11行);最后,若Candidate不为空,则从Candidate中随机选择一个染色体作为第2个父本,否则从Penalized中选择距离sj最远的染色体作为第2个父本(12行~16行)。
算法2基于动态阈值的父本选择算子。
1 输入:种群P={s1,…,sp}。
2 输出:{sj,sk}。
4 从Candidate中随机选择一个染色体sj
5 Candidate=Candidate{sj}
6 foreach I∈P{sj} do
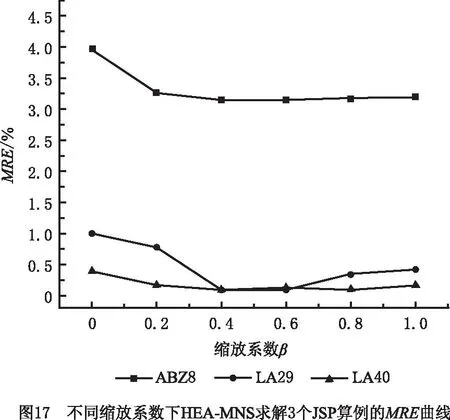
7 if Dpos(I,sj) 8 Candidate=Candidate{I}, 9 Penalized=Penalized∪{I} 10 end if 11 end foreach 12 if Candidate≠∅ then 13 从Candidate中随机选择一个个体sk 14 else 15 sk= argmax{Dpos(si,sj)|si∈Penalized} 16 end if 17 return{sj,sk} 作为混合进化算法的重要组件,交叉算子不仅要生成多样化的子代,还要将父辈的精英成分遗传给子代,因此本文不再采用单一的交叉方式,而是将基于最长相同子序列的交叉算子[5]与基于机器工序串的交叉算子[15]混合使用。每次交叉均随机选择一种交叉方法进行染色体重组。 为进一步增强种群的多样性,设计了一种基于动态惩罚阈值的种群更新策略。该策略的主要设计原则是在算法的初始阶段通过设定较大的惩罚阈值诱导更多样化的搜索,而在算法后期通过设定较小的惩罚阈值来强化集中搜索。 算法3给出了种群更新算法的伪代码,对于禁忌算法优化的两个子代{sp+1,sp+2}与当前种群P={s1,…,sp},本文采用以下规则来确定sp+1,sp+2是否应该替换原有种群的个体:首先,计算种群更新的惩罚阈值(3行),将{sp+1,sp+2}与P合并构建初始候选集合Candidate,选择目标值最小的个体添加到新种群中,并将该个体从Candidate中删除(4行~7行),初始化惩罚解集合Penalized(8行);然后,不断迭代,直到新种群的规模与原种群相同(9行~26行)。新种群个体选择过程如下:首先,计算候选集合中个体与新种群的距离(11行),然后将距离小于选择阈值D的个体从Candidate中删除并添加至Penalized(12行~16行);最后,若Candidate不为空,则从Candidate中选取目标值最优的个体进入新种群,否则从Penalized选择与新种群距离最远的个体进入新种群(17行~26行)。 算法3种群更新算子。 1 输入:种群P={s1,…,sp}和{sp+1,sp+2}。 2 输出:新种群NewPop。 3 计算当前种群的惩罚阈值D 4 初始化候选集合Candidate=P∪{sp+1,sp+2} 5 选择最优解Best=argmin{f(si)|si∈Candidate} 6 构建新种群NewPop={best} 7 Candidate=Candidate{best} 8 初始化惩罚解集合Penalized=∅ 9 while|NewPop| 10 foreach I∈Candidate do 11 I.dci=DCI(I,NewPop) 12 if I.dci 13 Candidate=Candidate{I} 14 Penalized=Penalized∪{I} 15 end if 16 end foreach 17 if Candidate≠∅ then 18 NewSelected =argmin{f(si)|si∈Candidate} 19 else 20 foreach I∈Penalized do 21 I.dci=DCI(I,NewPop) 22 end foreach 23 NewSelected=argmax{s.dci|s∈Penalized} 24 end if 25 NewPop=NewPop∪{NewSelected} 26 end while 27 Return NewPop 当惩罚阈值D较大时有利于增强搜索的广度,D值较小时有利于在有潜力的区域进行集中搜索。综合考虑以上特征,将D设定为随算法运行时间线性减少的动态值,使算法逐渐从多样化搜索转化为集中化搜索, (28) 式中:Tcur为当前运行时间;Ttotal为算法设定的最大运行时间;β为缩放系数,β=0.5;P0为初始种群。 假设种群个体数为N、工件数量为n、机器数量为m。算法步骤包括种群的初始化、交叉父本匹配选择操作、交叉操作、禁忌搜索操作、解码操作、种群更新操作。算法采用随机生成方法构建初始种群,该过程的时间复杂度为O(n×m×N);由于交叉父本匹配选择操作与种群更新操作均需计算种群密度,根据个体之间的距离计算公式可得其在最坏情况下的复杂度为O(n2×m),个体与种群其他个体的距离最小值计算的时间复杂度为O(N×n2×m),进而可得种群密度的计算复杂度为O(N2×n2×m);交叉匹配选择操作将种群随机分为两组的时间复杂度为O(N),最坏情况下,查找另一组中距离第1个父本最远个体的时间复杂度为O(N);算法随机执行两种交叉操作,每种交叉操作均需访问父染色体两次,同时每次迭代只执行1次交叉操作,因此交叉操作的时间复杂度为O(n×m);禁忌搜索操作中邻域操作的时间复杂度为O(n×m2),近似评价的时间复杂度为O(n×m),因此禁忌搜索操作的时间复杂度为O(n2×m3);在解码过程中,每道工序需要从前后获取空闲时间段,因此最坏情况下,该操作的时间复杂度为O(n2×m);在种群更新过程中,由于每次迭代只产生两个子代个体,需要重新计算子代个体与原种群个体之间的距离,该过程的时间复杂度为O(N×n2×m),依次添加个体进入新种群过程的时间复杂度为O(N2)。由于初始种群构建与初始种群密度计算只执行一次,对算法整体性能影响不大,从以上分析可知,算法迭代过程中在禁忌搜索操作与种群更新操作上消耗的时间最多。 HEA-MNS采用C++编程实现,并在Linux操作系统的计算机(CPU主频2.3 GHz,内存16 GB)上使用g++编译运行。算法参数设置如下:算法执行的总时间为10 min,种群规模为50,禁忌搜索的终止条件为未改进迭代次数达到1 000次;禁忌长度在两个极值之间随机选取,极值的设置分别为Lmin=0.5(10+n/m)和Lmax=1.5(10+n/m),其中n和m分别为工件数和机器数。考虑到HEA-MNS的随机特性,本文独立求解每个问题算例10次。测试实验包括两组JSP基准算例,均来源于JSP基准算例库(http://jobshop.jjvh.nl/)。第1组为LAWRENCE[39]设计的40个算例(LA01~LA40),第2组为ADAMS等[40]设计的5个基准算例(ABZ05~ABZ09)。 ImpNS= (29) 采用N5,sCET+2MT,N6,N7,PN7+2MT 5种邻域结构对45个JSP算例的测试结果进行统计,如表2所示。表中算例顺序按照PN7+2MT邻域结构的相对改进百分比Imp降序排列得到,并以该顺序对算例进行编号。按照该顺序,绘制sCET+2MT,N6,N7,PN7+2MT 4种邻域结构的相对改进百分比曲线,如图14所示。对于所有45个JSP算例,PN7+2MT的相对改进百分比曲线均位于N6与N7邻域结构之上,说明多工序精确联动可有效改善邻域结构性能。与sCET+2MT邻域结构相比,PN7+2MT的相对改进百分比曲线具有明显优势,说明更大范围的工序参与联动操作可以大幅提升邻域结构的搜索能力。 表2 4种邻域结构的相对改进百分比对比 同一规模下,对各算例应用不同邻域结构产生邻域解的数量(SNS)av进行统计分析,结果如表3所示,其中:CR表示PN7+2MT相对于N7邻域结构的邻域解数量的消减率,计算公式如式(30)。因为sCET+2MT邻域结构是在N5的基础上联动另外两对工序,其邻域解的数量相同,所以只列出N5的邻域解数量。从表3可见,PN7+2MT的邻域解数量大于N5和N6,表明PN7+2MT对解空间具有广泛搜索的能力。相对于N7,PN7+2MT的邻域规模减小约14%,说明所提无效移动判定条件可有效减少邻域规模。 表3 4种邻域结构的邻域解数量对比 (30) 从LA算例集中选取10个求解比较困难的算例测试算法性能,结果如表4所示,表中参数的详细描述如下:Best为10次求解结果的最优值;Mav为10次求解结果的平均值;Tav(s)为10次获得求解结果的平均用时(单位:s);MRE为求解结果UBsolve与已知下界LB相对偏差的平均值,其中相对偏差RE的计算如式(31)所示。表4的4个对比算法分别为文献[41]具有局部搜索策略和多交叉算子的改进遗传算法(Multi-Crossover Local Search Genetic Algorithm,MXLSGA)、文献[42]基于多算子通信的序列禁忌搜索差分进化(Multi-operator Communication based Differential Evolution with sequential Tabu Search approach,MCDE/TS)算法、文献[21]基于无延迟调度路径重连与回溯禁忌搜索算法(Path Relinking based on Non-Delay scheduling and Backtracking Tabu Search algorithm,PRND/BTS)、文献[22]基于切换策略的混合进化算法(Switching strategy-based Hybrid Evolutionary Algorithms,SHEA)。 表4 10个困难LA算例测试结果与其他算法结果比较 RE=(UBsolve-LB)/LB×100 (31) 从表4可知,HEA-MNS求得的最优结果Best与LB相对偏差的平均值b-MRE为0.01,且均低于其余4种算法的b-MRE。同时,HEA-MNS对其中9个算例的最优结果均优于或等于其他4种算法,仅对LA29算例的求解结果劣于SHEA算法。HEA-MNS求得的最优结果平均值Mav与LB相对偏差的平均值av-MRE均小于其他4种算法的b-MRE。 表5总结了HEA-MNS与其他4种算法求解全部LA算例的比较结果。实验结果表明,HEA-MNS对每组算例求得的b-MRE优于或等于MXLSGA,MCDE/TS,PRND/BTS 3种算法,由于HEA-MNS未能求得LA29算例的已知最优解,使其在LA26-30算例组获得的b-MRE值劣于SHEA算法,同时HEA-MNS对全部LA算例的av-MRE均小于其他4种算法的b-MRE,验证了本文算法的稳定性。 表5 LA算例测试结果与其他算法结果比较 表6所示为对5个ABZ基准算例的测试结果,4种对比算法包括文献[41]的MXLSGA算法、文献[43]基于增强Lévy飞行和差分进化的混合鲸鱼优化算法(hybrid Whale Optimization Algorithm enhanced with Lévy Flight and Differential Evolution,WOA-LFDE)、文献[22]的SHEA算法、文献[44]基于频率分析算子的遗传算法(Genetic Algorithm based on Frequency Analysis operator,FAGA)。从MRE角度进行统计对比分析,由于SHEA 算法未给出ABZ7算例的测试结果,在计算b-MRE时,设置该基准算例的相对偏差RE=0。HEA-MNS的b-MRE和av-MRE分别为0.62和0.73,其余3种算法的b-MRE分别为4.46,0.92,1.07,2.10,均大于本文算法。HEA-MNS求得了3个基准算例(ABZ5,ABZ6,ABZ9)的下界值,算例ABZ8的求解最优结果为667,其余4种算法分别为713,669,669,713,算例ABZ9的求解最优结果为678,其余4种算法分别为721,683,685,680,验证了本文算法的有效性。图15和图16所示分别为HEA-MNS获得ABZ8和ABZ9基准算例最优调度结果的甘特图。 表6 ABZ算例测试结果与其他算法结果比较 为了维持种群多样性,通常需要在进化算法设计中添加额外的参数。在HEA-MNS中需要设置惩罚阈值D,该值越高,对决策空间的多样化探索能力越强。由式(29)可知,惩罚阈值D由算法执行时间、初始种群密度与缩放系数β共同决定,上述测试中的β均设置为0.5。为了探讨β对HEA-MNS性能的影响,将其设置6个级别{0,0.2,0.4,0.6,0.8,1.0},选用比较困难的ABZ8,LA29,LA40作为测试算例,算法其他参数设置与4.2节相同,图17所示为不同β值下HEA-MNS求解3个测试算例的MRE曲线图。 从图17可知,3个测试算例的MRE值在β=0时最差,说明当HEA-MNS缺乏有效的种群多样性控制策略时,算法性能会受到明显影响;当β≥0.4时,算法均能保持较优的性能,说明在保证算法性能的前提下,β的取值范围很大,HEA-MNS具有较强的稳定性。 本文提出一种HEA-MNS算法,通过将基于多工序精确联动邻域结构的禁忌搜索算法与多样化控制的进化算法相结合,有效地解决了传统进化算法在求解JSP中出现的局部搜索能力差、易早熟等问题。 本文从理论上给出了N7邻域结构中工序无效移动的判定条件,据此设计了3对工序精确联动的邻域结构,有效扩展了邻域搜索的范围。为了解决传统进化算法的种群多样性随进化过程快速下降的问题,本文提出基于邻域惩罚的父本选择算子与基于动态惩罚阈值的种群更新策略,有效提高了子代与种群的多样性。 通过对比HEA-MNS与多种先进算法对不同规模JSP基准算例的测试结果,证明了算法的稳定性与有效性。然而,当前工作仅对算法进行了改进,并在静态基准算例上进行了测试,初步验证了HEA-MNS的可行性与有效性,下一步拟将HEA-MNS应用于实际生产调度场景,并考虑不确定因素的影响。3.5 种群更新算子
3.6 算法复杂度分析
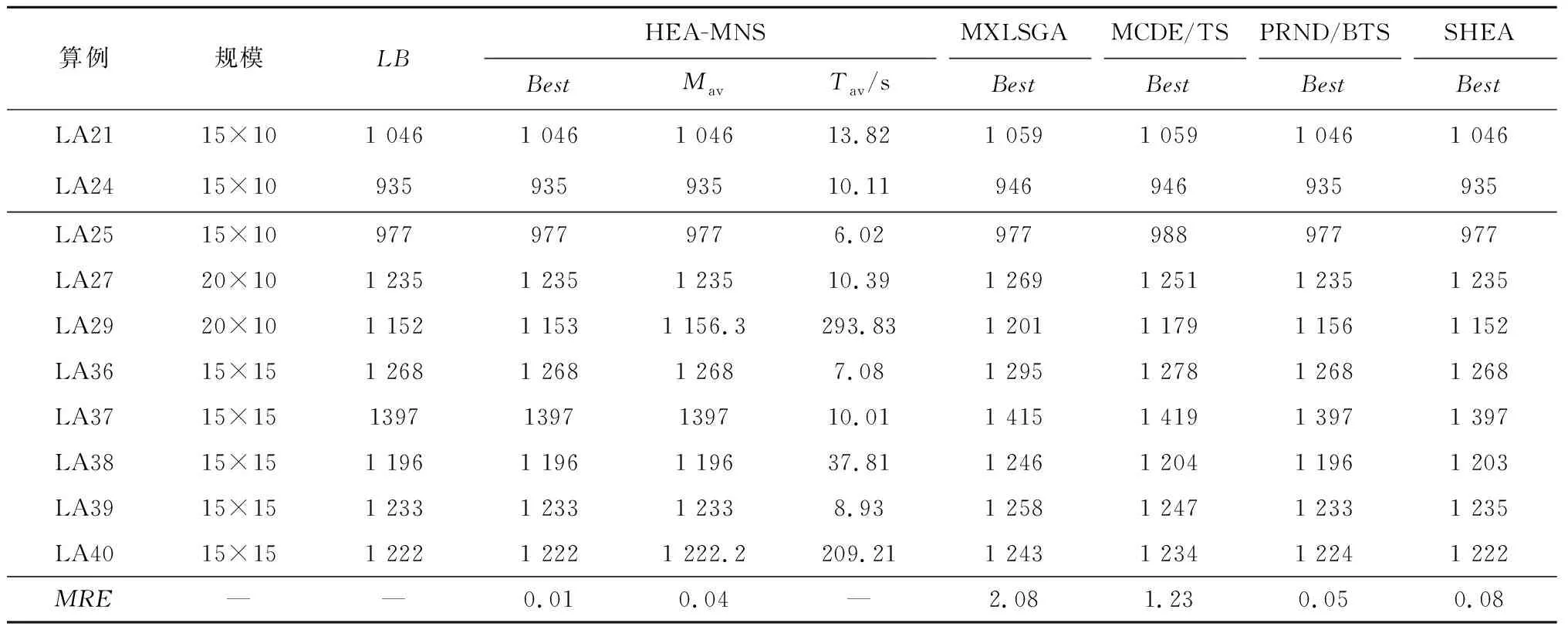
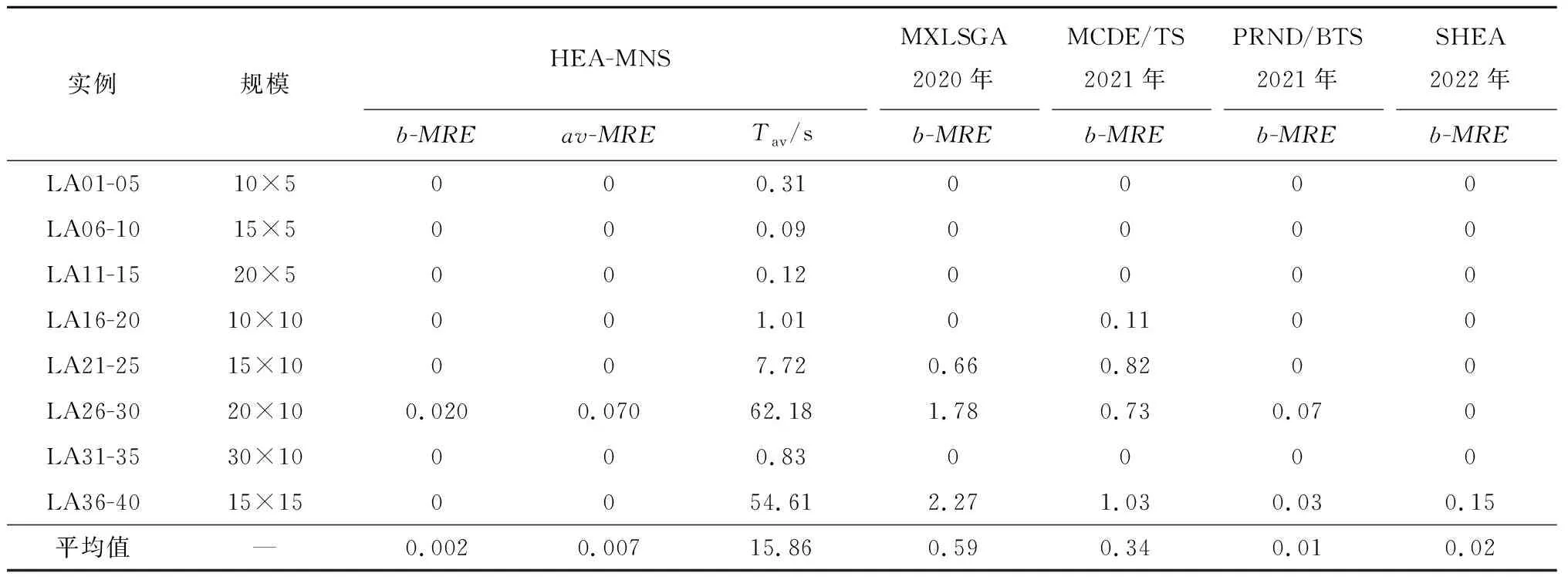
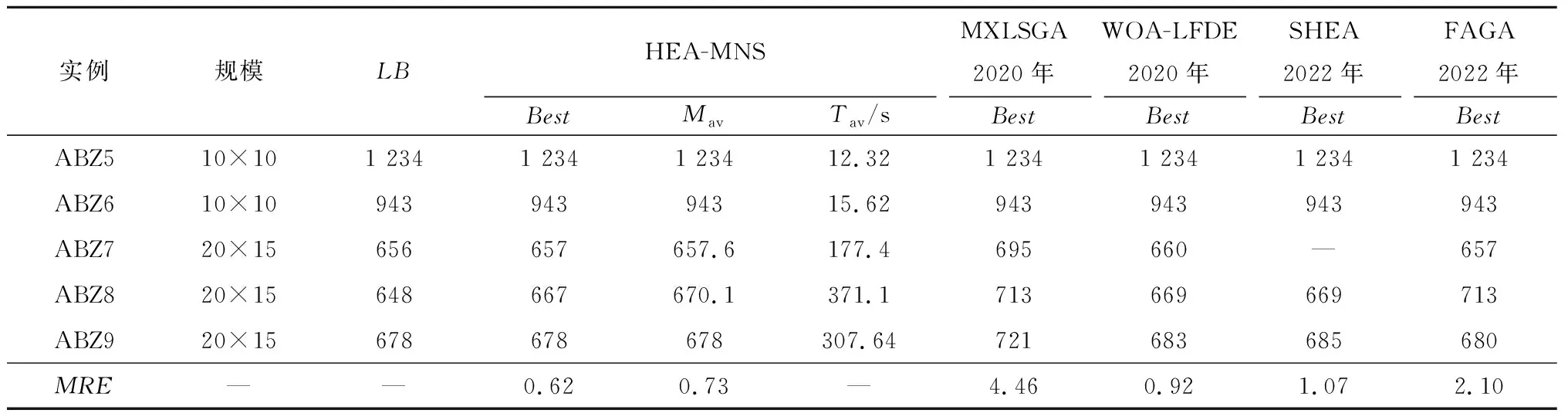
4 算法测试
4.1 邻域结构测试
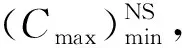
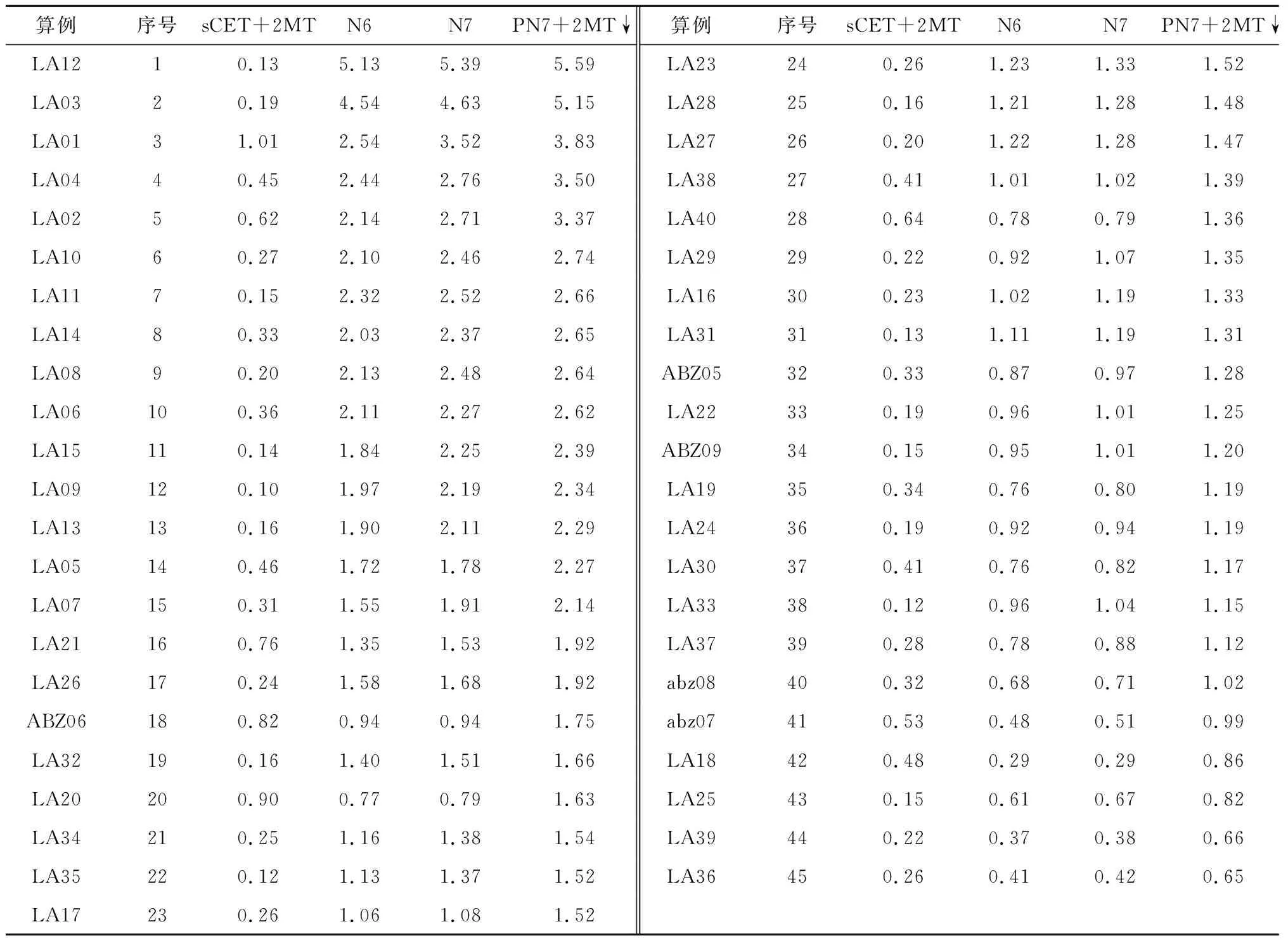
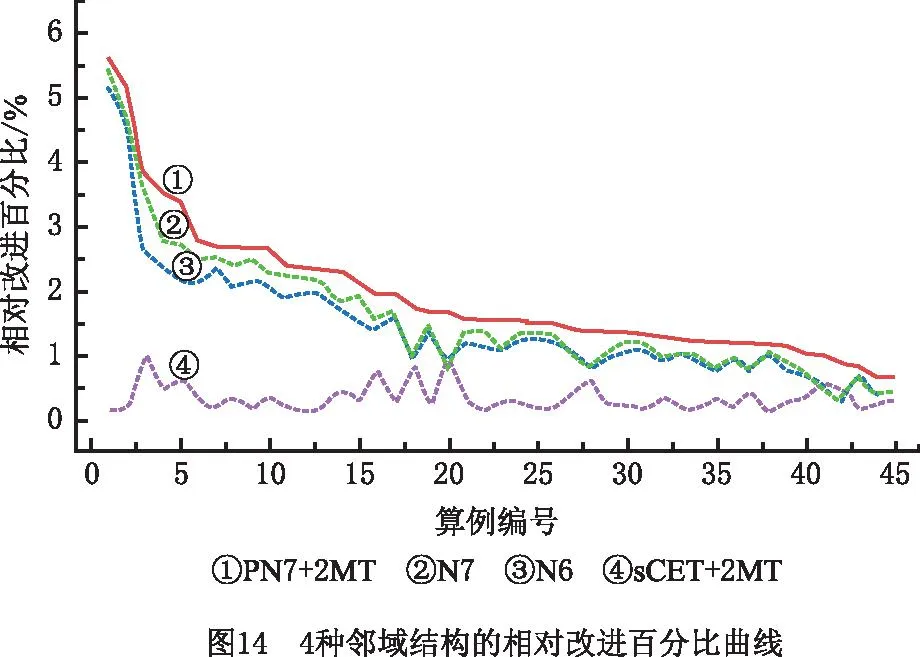
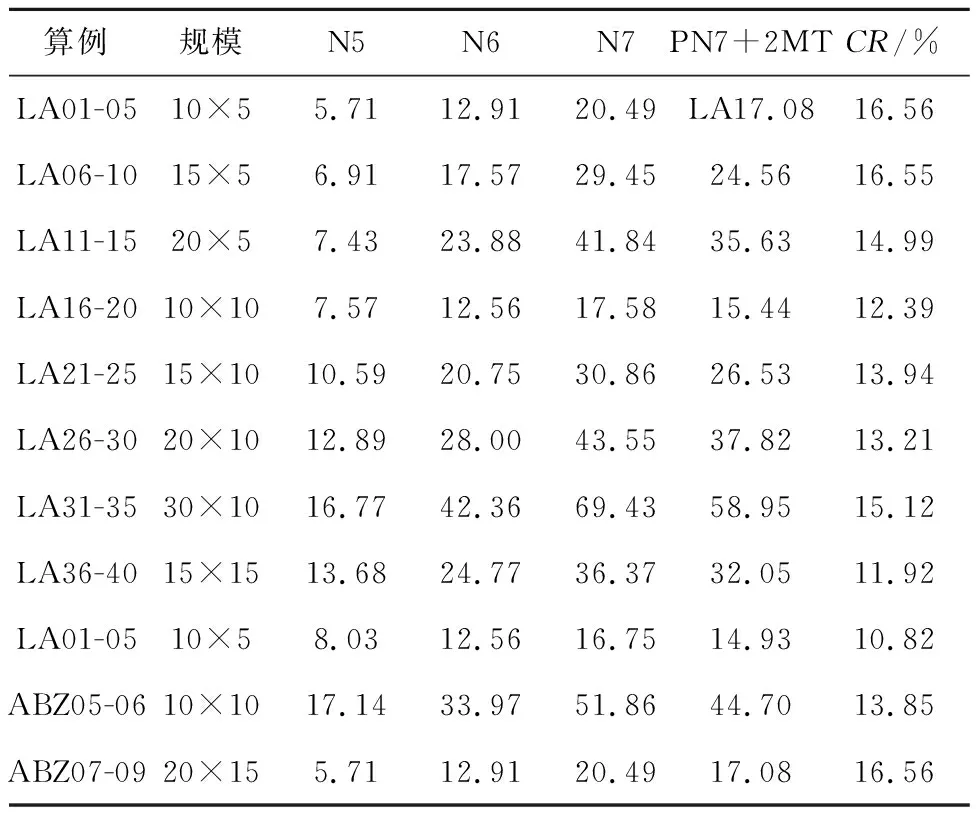
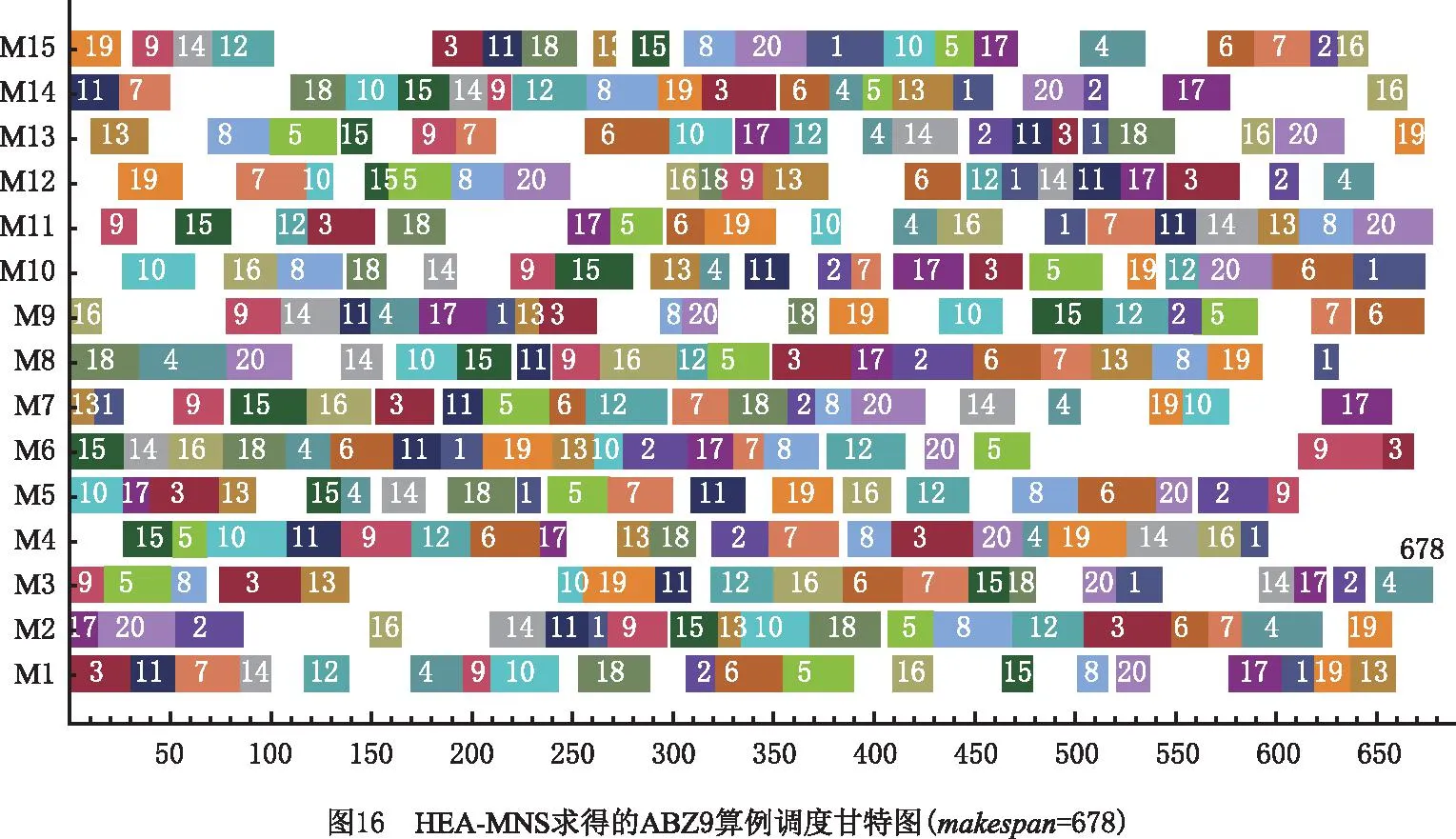
4.2 算法性能测试

4.3 参数敏感度分析
5 结束语
