周转箱多模型系统的鲁棒切换策略

张松涛,向瑞雪,张 敏

(1.临沂大学 物流学院,山东 临沂 276005;2.山东科技大学 交通学院,山东 青岛 266590;3.临沂大学 图书馆,山东 临沂 276005)

0 引言

近年来,越来越多的纸箱和木箱等一次性物流包装物令脆弱的生态环境不堪重负。相对于一次性物流包装物,周转箱包装成本低、绿色环保、可循环使用,能够实现物流容器的通用化和一体化管理,已经逐渐成为生产和流通企业进行物流现代化管理的必备品之一。然而,低周转率直接导致周转箱的周转成本较高,例如,虽然郑州市的蔬菜周转箱保有量有1 500多万个,但是在一些大型蔬菜批发市场中却常见堆积如山的蔬菜周转箱[1]。因此,需要设计多种有效的周转箱运作模式,通过提高周转率来普及周转箱,以加快我国物流现代化进程。

为了提高周转箱的效率,王城坡等[2]提出周转箱循环共享模式来提高周转箱的利用率,章军等[3]设计了一种可循环使用的塑料瓦楞板组合式周转箱来提高运输效率,而苌道方等[4]则通过优化周转箱的配载模式来提高利用率。周转箱从最初生产到最终使用这一过程构成了一个由制造商、运营商和客户组成的供应链系统,上述文献并未在供应链系统中考虑周转箱的运作问题。由于客户不确定需求和多种提前期的干扰,具有较高鲁棒性的周转箱供应链系统能够使系统中的各种变量在一定时间内回归正常的稳定状态;反之,鲁棒性较低的系统则会出现周转箱库存积压或短缺,增大供应链系统的成本。因此,在节点企业的不同周转箱库存状态下,需要设计一种在不同周转箱运作模式间切换的鲁棒切换策略,使周转箱供应链系统低成本稳定运行。

截至目前,共有以下3种提高供应链鲁棒性的运作策略:

(1)许多学者从优化的角度研究了静态供应链系统的鲁棒运作策略。对于供应链优化设计,HEIDARI-FATHIAN等[5]应用随机鲁棒优化策略协调血液供应链网络规划中的总成本和温室气体排放量;李进[6]提出一种多目标鲁棒模糊优化策略来解决低碳经济环境下多级闭环供应链网络设计的设施选址和配置问题;基于布谷鸟优化算法,SANGAIAH等[7]设计了一种液化天然气供应链鲁棒优化策略。对于供应链的优化运作,邱若臻等[8]基于经济增加值提出一种供应链销售与运营计划鲁棒优化策略;JABBARZADEH等[9]研究了一种双目标鲁棒优化策略,以最小化供应链成本和温室气体排放量;ABBASSI等[10]研究了一种联合货运鲁棒优化策略,以解决供应链中运输成本和运输承包商运输能力的不确定性问题。鲁棒优化策略主要针对静态供应链系统的决策策略,而鲁棒控制策略对抑制各种扰动对动态供应链系统的影响比鲁棒优化策略更有效。

(2)少部分学者从控制的角度研究了动态单模型供应链的鲁棒运作策略。徐君群[11]基于线性矩阵不等式研究了一种需求不确定性下闭环供应链动态网络的鲁棒H∞控制策略;LI等[12]研究了一种抑制不确定供应链牛鞭效应的鲁棒控制策略;靖可等[13]研究了一种不确定提前期扰动下三层动态供应链系统的鲁棒H∞控制策略;NAV等[14]提出一种抑制供应链网络混沌行为的鲁棒控制策略。上述文献是基于单模型供应链设计的鲁棒控制策略。供应链系统内外不确定因素和提前期因素导致节点企业的库存水平经常变化,节点企业针对不同库存水平将采取相应的生产和订购策略来降低成本。因此,供应链系统实际上是一个动态切换系统。相对于多模型供应链系统,单模型供应链系统难以精确描述供应链系统的全部动态特性。

(3)极少数学者从切换控制的角度研究了动态多模型供应链的鲁棒运作策略。切换控制从切换方式上分为硬切换和软切换两种。硬切换是系统通过跳变的方式将一种工况直接切换到另外一种工况[15]。对于硬切换在供应链中的应用,葛汝刚等[16]对不确定闭环供应链设计了一种在自行回收和第三方回收之间切换的鲁棒策略;刘春玲等[17]基于库存切换提出一种鲁棒切换策略来抑制多供应链库存决策系统的牛鞭效应;李庆奎等[18]设计了一种Markov鲁棒切换策略来抑制回收再制造不确定闭环供应链的牛鞭效应;ZEMZAM等[19]在多重时变提前期和不确定需求下提出一种在二级供应链网络拓扑间切换的鲁棒策略。由于硬切换的切换过程瞬间完成且没有过渡过程,导致系统变量在切换过程中出现较大波动,降低了系统的动态性能,不利于系统平稳运行。软切换一般采用加权函数将各个控制单元进行线性组合后作为控制输出,其能够减少硬切换下工况切换给系统带来的扰动[20]。

日本学者TAKAGI等[21]提出一种Takagi-Sugeno模糊控制模型,该模型可用一组IF-THEN模糊规则来描述多模型动态系统。鉴于IF-THEN模糊规则的隶属度函数可以在多模型间实现软切换,基于Takagi-Sugeno模糊控制理论,本文提出一种周转箱供应链动态多模型系统的鲁棒软切换策略。本文的主要研究内容如下:①分别构建包括制造商、运营商和客户的周转箱供应链系统和周转箱供应链网络系统,这两个系统既考虑了周转箱从制造商到运营商再到客户的正向流动,又考虑了周转箱从客户到运营商的逆向流动;②考虑制造商生产周转箱的生产提前期、运营商订购周转箱的订购提前期、客户返还周转箱的还箱提前期和客户对周转箱的不确定需求,分别构建周转箱供应链系统和周转箱供应链网络的动态演变基本模型;③通过周转箱的链内横向转运、链间横向转运和链间订购等模式,设计10种周转箱生产运作模式及其切换策略;④应用Takagi-Sugeno模糊控制模型统一表示周转箱供应链系统和周转箱供应链网络系统,并提出一种周转箱模糊系统的鲁棒控制策略;⑤通过6个仿真实验检验由周转箱的鲁棒控制策略与切换策略组成的鲁棒切换策略的有效性。

1 模型描述

本文模型主要变量的含义如表1所示。

表1 主要变量的含义

续表1

1.1 周转箱供应链模型

1.1.1 周转箱供应链基本模型

考虑由1个制造商、N个运营商和N个客户组成周转箱供应链系统。该系统不仅考虑了制造商生产、运营商订购和供应、客户使用周转箱的正向通道,还考虑了运营商回收、修复、废弃周转箱的逆向通道。为了减少运营商之间周转箱库存不平衡,以降低成本和提高周转箱的周转率,供应链内的运营商之间可以横向转运周转箱,而且如果本链内的制造商无法满足运营商正常订购周转箱的需求,运营商可以向其他供应链的制造商紧急订购周转箱。因此,在周转箱供应链系统中,运营商有正常订购模式、紧急订购模式、正常横向转运模式、供应模式、回收模式、修复模式和废弃模式7种运作模式。基于以上内容,本文设计的周转箱供应链系统的微观结构如图1所示。

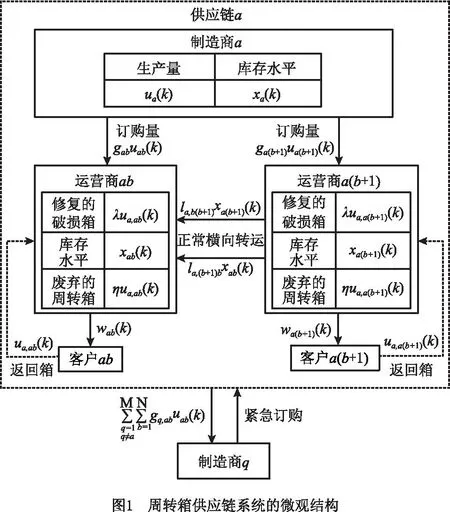
考虑制造商生产周转箱的生产提前期、运营商订购周转箱的订购提前期、客户返还周转箱的还箱提前期和客户的不确定周转箱需求,建立如下周转箱供应链系统的库存状态和系统总成本动态演变基本模型:

(1)

(2)

其中:式(1)和式(2)中的每个变量均表示为偏差值,即实际值和标称值之差;因为对不同周转箱库存状态节点企业将执行不同的运作模式,所以式(1)和式(2)在不同周转箱库存状态下将采用不同的表达式。

1.1.2 周转箱供应链的库存切换策略

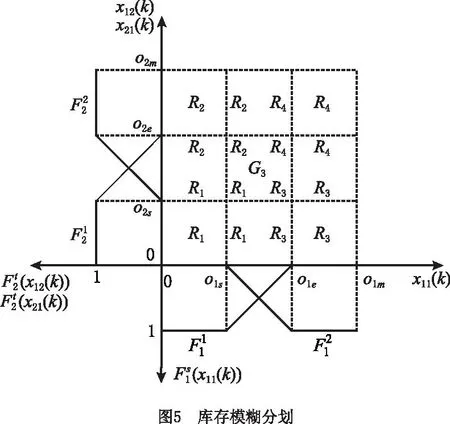
为了在提前期和不确定需求下保持周转箱供应链系统低成本运行,基于运营商周转箱的安全库存值和期望库存值,在供应链中设计如图2所示的运营商周转箱运作切换策略。

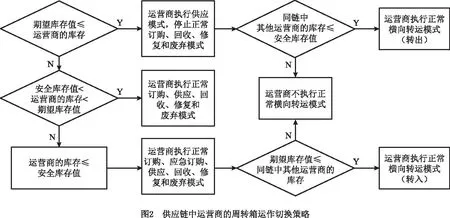
相应地,供应链中制造商的周转箱生产切换策略设计如下:如果每个运营商的周转箱库存均大于或等于各自的期望库存值,则所有制造商均不生产周转箱;如果每个运营商的周转箱库存均小于或等于其安全库存值,则所有制造商都紧急生产周转箱;如果周转箱库存小于或等于其安全库存值的运营商请求紧急订购模式,则其他供应链中的制造商将紧急生产周转箱。除上述3种情况外,制造商正常生产周转箱。供应链中运营商的周转箱运作切换策略和制造商的周转箱生产切换策略构成了周转箱供应链的库存切换策略。

1.1.3 周转箱供应链多模型系统

对于在客户不确定需求和多提前期下不断变化的节点企业周转箱库存水平,基于式(1)和式(2)的基本模型、运营商的运作切换策略和制造商的生产切换策略,周转箱供应链系统的第i个模型可用矩阵形式表示如下:

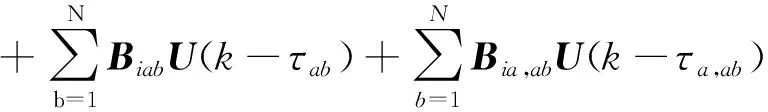
(3)

式中各向量和系数矩阵的表达式详见附录1。

1.2 周转箱供应链网络模型

1.2.1 周转箱供应链网络基本模型

由M个周转箱供应链系统组成的周转箱供应链网络的微观结构如图3所示。在周转箱供应链网络中,除了考虑周转箱供应链系统中运营商的7种周转箱运作模式外,增加了一种链间运营商之间的紧急横向转运模式。

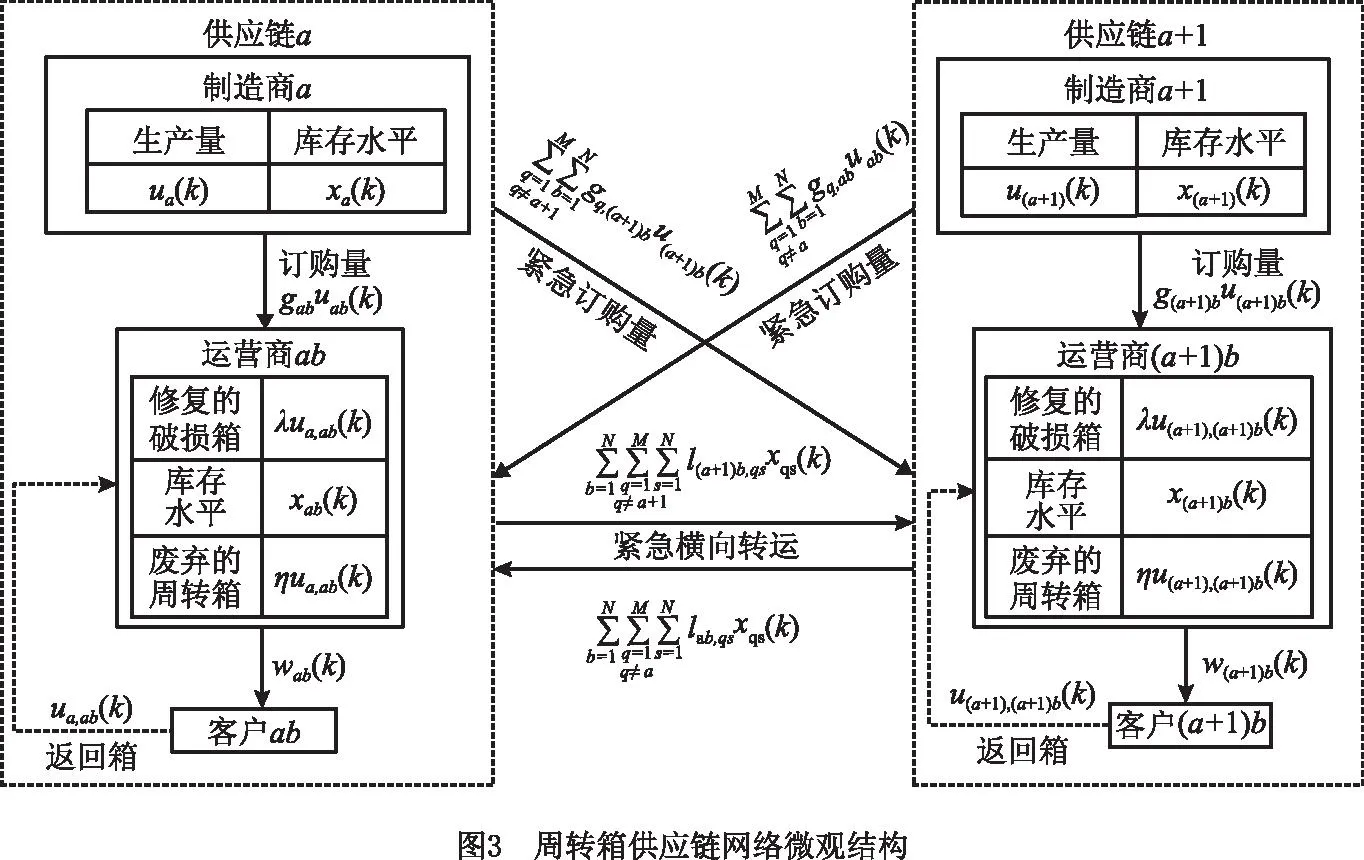
基于式(1)和式(2),建立周转箱供应链网络的库存状态和系统总成本动态演变基本模型如下:

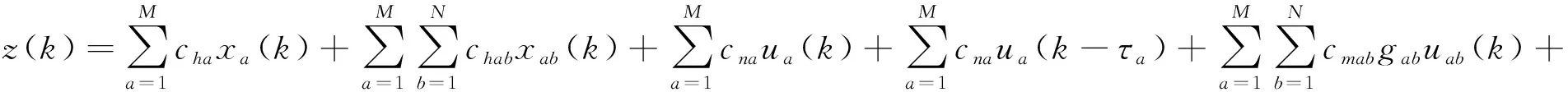
(5)

其中:式(4)和式(5)中的每个变量均为偏差值,即实际值和标称值之差;因为对不同周转箱库存状态节点企业将执行不同的运作模式,所以式(4)和式(5)在不同周转箱库存状态下将采用不同的表达式。

1.2.2 周转箱供应链网络的库存切换策略

考虑在不同供应链运营商之间的周转箱紧急横向转运,基于图2设计的供应链网络中运营商的周转箱运作切换策略如图4所示,而供应链网络中制造商的周转箱生产切换策略同供应链系统中制造商的周转箱生产切换策略。

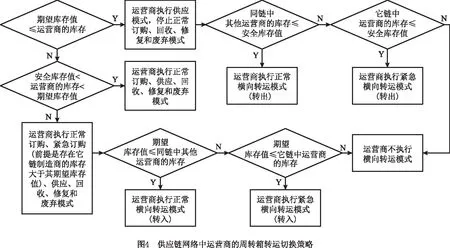
1.2.3 周转箱供应链网络多模型系统

在周转箱供应链网络中,基于式(4)和式(5)的基本模型、运营商的运作切换策略和制造商的生产切换策略,周转箱供应链网络的第i个模型可用矩阵形式表示如下:

式中各向量和系数矩阵的表达式详见附录1最后一段内容。

2 周转箱多模型系统鲁棒控制策略

为了使节点企业根据自身不同的周转箱库存水平而在不同的周转箱运作模式间切换,应用Takagi-Sugeno模糊控制系统将式(6)的周转箱供应链网络多模型系统表示如下:

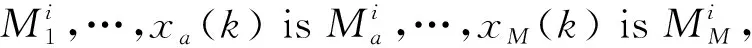
(7)

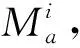
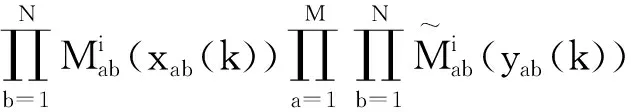
如果式(7)中的M=1,则式(7)表示周转箱供应链多模型系统。

采用并行分布补偿控制算法为含多提前期的周转箱网络各模型设计的局部周转箱库存反馈控制律

如下:

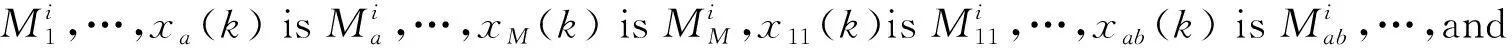
(8)

式中:Ki为状态反馈增益矩阵;Kia为含提前期τa的状态反馈增益矩阵;Kiab为含提前期τab的状态反馈增益矩阵;Kia,ab为含提前期τa,ab的状态反馈增益矩阵;i=1,2,…,r,a=1,2,…,M,b=1,2,…,N。

如果式(8)中的M=1,则式(8)也不是周转箱供应链系统的局部周转箱库存反馈控制律。

为了提出适合周转箱模糊多模型系统(7)的鲁棒控制策略,将文献[22]中的定理1修改如下:

定理1对于给定的表征鲁棒性大小的实数γ(‖供应链成本‖2/‖客户需求‖2≤γ),如果在最大交叠规则组[23]Gc中存在对称正定矩阵Pc和Qac,以及矩阵Kic,Kjc,Kiac,Kiabc,Kia,abc,Kjac,Kjabc,Kja,abc满足如下矩阵不等式,则存在式(8),使满足标准模糊分划[23]的式(7)在性能指标γ下鲁棒渐近稳定。

(9)

(10)

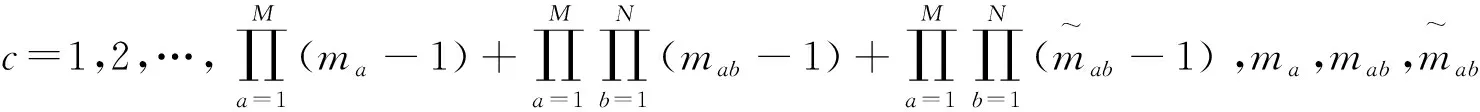
对于适当的参数γ,通过定理1不仅可以求解出对称正定矩阵Pc和Qac,以表明周转箱供应链网络鲁棒稳定,还可以得到周转箱库存状态反馈增益矩阵,进而实现周转箱多模型系统的闭环负反馈控制,以抑制多提前期和客户不确定需求对周转箱供应链网络的影响。因此,定理1所示的鲁棒控制策略结合制造商的生产切换策略和运营商的运作切换策略,可以形成适用于周转箱多模型系统的鲁棒切换策略。

3 仿真分析

为验证本文所设计的周转箱多模型系统鲁棒切换策略的有效性,选取某汽车零部件的2个周转箱供应链构成的网络作为仿真对象,分别在同一供应链内和不同供应链间进行仿真实验。为了简化计算,用τ1,τ2,τ3分别表示所有制造商的生产提前期、所有运营商的订购提前期和所有客户的还箱提前期。

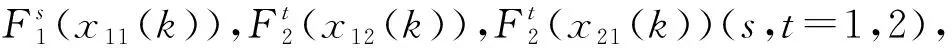
根据汽车零部件周转箱供应链网络的实际运行情况,设置的仿真实验的通用系统参数详见附录2。

3.1 供应链内仿真实验

在以下仿真实验中,选择周转箱供应链1中的制造商1、运营商11、运营商12、客户11和客户12为研究对象,并将周转箱供应链2中的制造商2作为战略供应商,则周转箱供应链1中的库存状态转移方程和系统成本转移方程表示如下:

(11)

z(k)=ch1x1(k)+ch11x11(k)+ch12x12(k)+cn1u1(k)+cn1u1(k-τ1)+cm11g11u11(k)+cm11g11u11(k-τ2)+
cm12g12u12(k)+cm12g12u12(k-τ2)+cm211g2,11u11(k)+cm211g2,11u11(k-τ2)+cm212g2,12u12(k)+
cm212g2,12u12(k-τ2)+cc112l1,12x12(k)+cc121l1,21x11(k)+cd11u1,11(k)+cd11u1,11(k-τ3)+
cd12u1,12(k)+cd12u1,12(k-τ3)+cr11λu1,11(k)+cr11λu1,11(k-τ3)+cr12λu1,12(k)+
cr12λu1,12(k-τ3)+co11ηu1,11(k)+co11ηu1,11(k-τ3)+co12ηu1,12(k)+co12ηu1,12(k-τ3)。

(12)

将式(11)和式(12)转化为如下模糊控制系统:

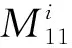
(13)

式中:a=1,b=1,2。在不同模糊规则下,系统的参数设置详见附录3。

设计式(13)的周转箱库存状态反馈控制律为:

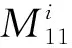
式中:a=1,b=1,2。

通过求解定理1中的式(9)和式(10),可得如下正定矩阵P1,Q11,Q21,Q31,因此由制造商1、运营商11、运营商12、客户11和客户12组成的周转箱供应链1是鲁棒渐近稳定的。下面针对表2中3种不同的初始值和标称值进行仿真实验。

表2 仿真实验1～仿真实验3的初始值和标称值

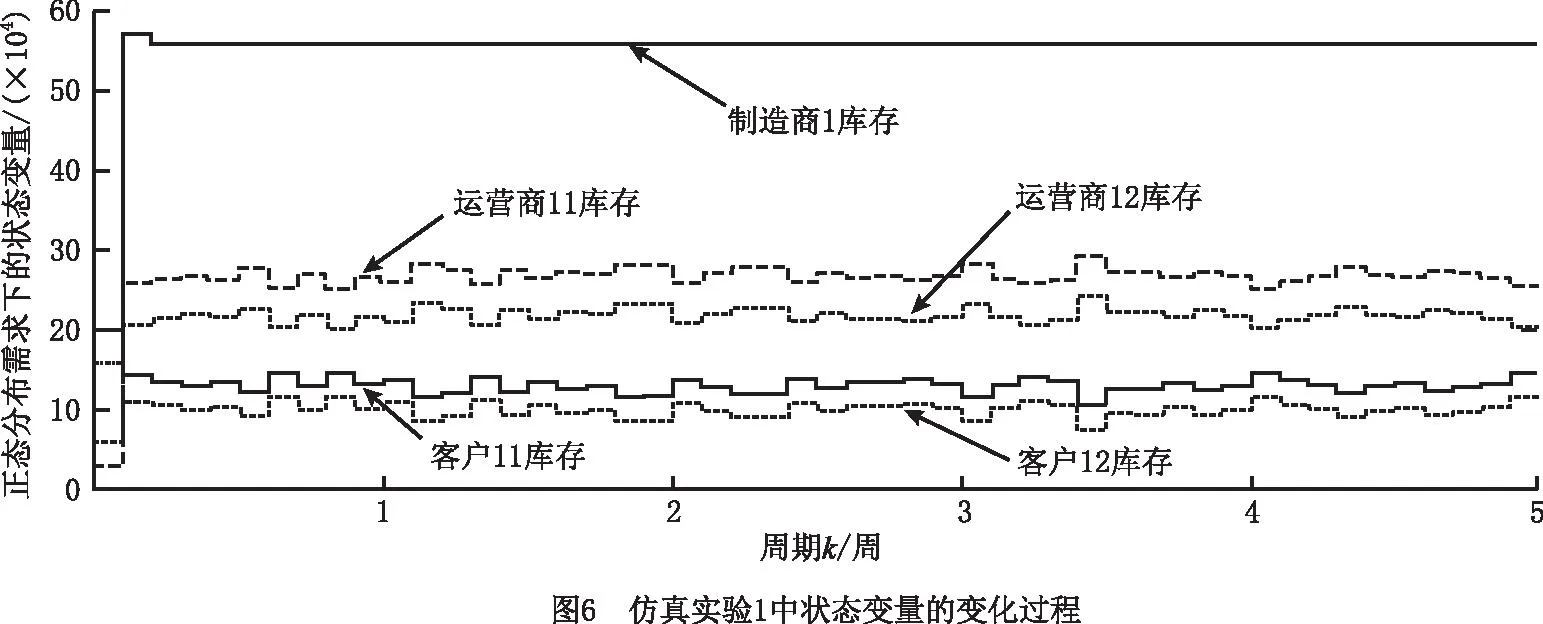
(1)仿真实验1 实验结果如图6～图8所示。对于运营商11和运营商12的初始库存均小于各自安全库存值的情况,为了满足客户需求,制造商1执行正常生产模式,运营商11和运营商12执行正常订购模式、紧急订购模式、供应模式、回收模式、修复模式和废弃模式,因此制造商1、运营商11和运营商12的库存迅速增加,客户11和客户12的库存水平快速减少。当运营商11和运营商12的库存达到各自安全库存值和期望库存值之间时,两个运营商的紧急订购模式均停止,系统达到稳定状态。

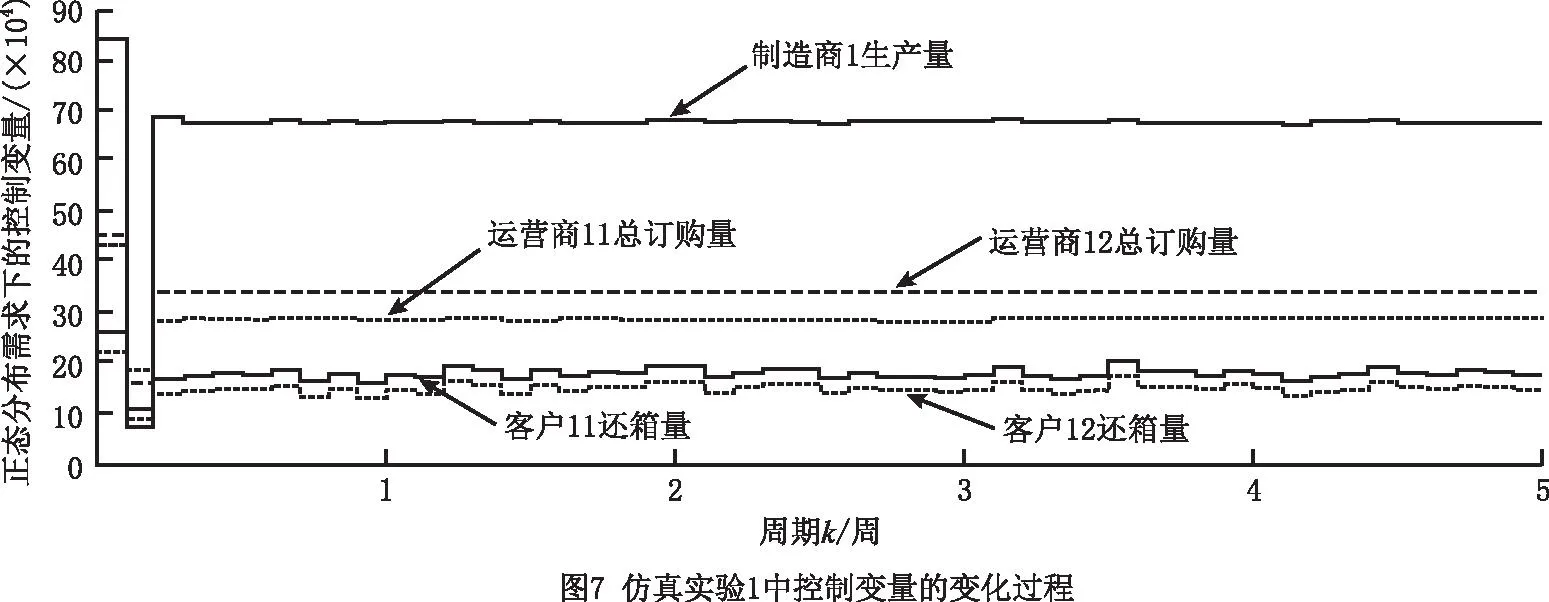
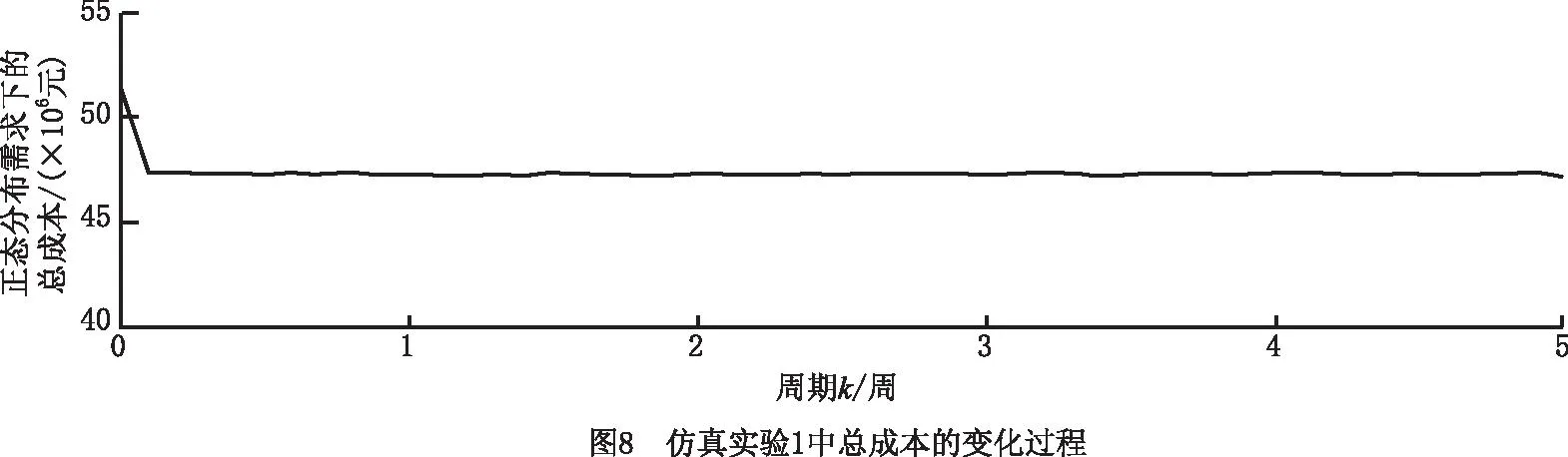
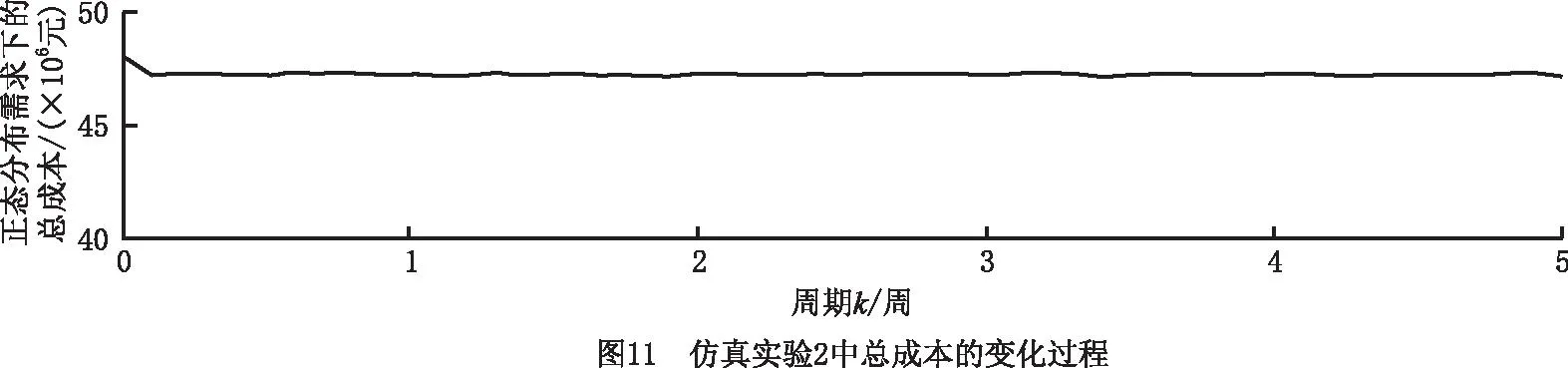
(2)仿真实验2 实验结果如图9～图11所示。对于运营商11初始库存大于其期望库存值,而运营商12的初始库存小于其安全库存值的情况,为了满足客户需求,减少库存积压,降低库存成本,在系统运作初期,制造商1执行正常生产模式,运营商11仅执行供应模式和正常横向转运模式(将周转箱转运至运营商12),而运营商12则执行正常订购模式、紧急订购模式、正常横向转运模式(从运营商11转运周转箱)、供应模式、回收模式、修复模式和废弃模式,因此制造商1、运营商12和客户11的库存迅速增加,运营商11和客户12的库存水平快速减少。当运营商11和运营商12的库存达到各自安全库存值和期望库存值之间时,运营商11停止正常横向转运模式(将周转箱转运至运营商12),并开始正常订购模式、供应模式、回收模式、修复模式和废弃模式,而运营商12则停止紧急订购模式和正常横向转运模式(从运营商11转运周转箱)。最终系统中的库存量、生产量、订购量、还箱量和系统总成本均稳定在一定水平。

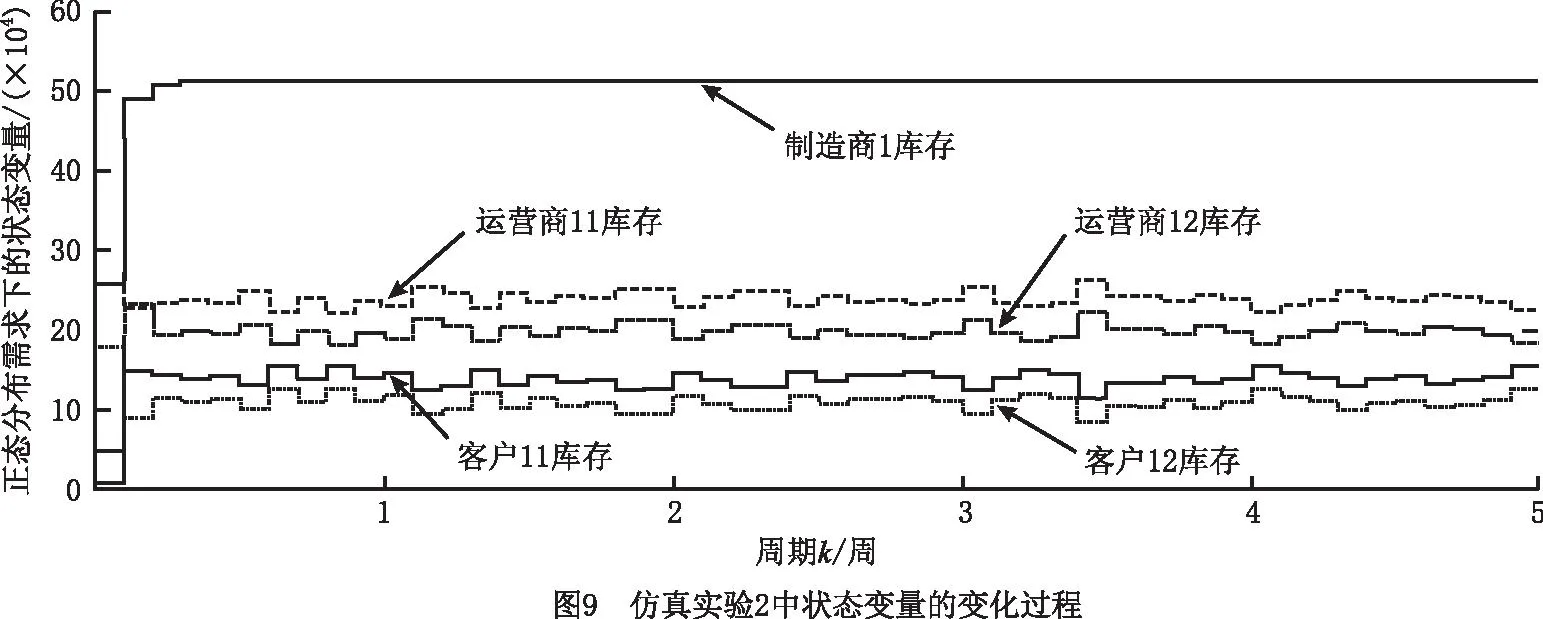
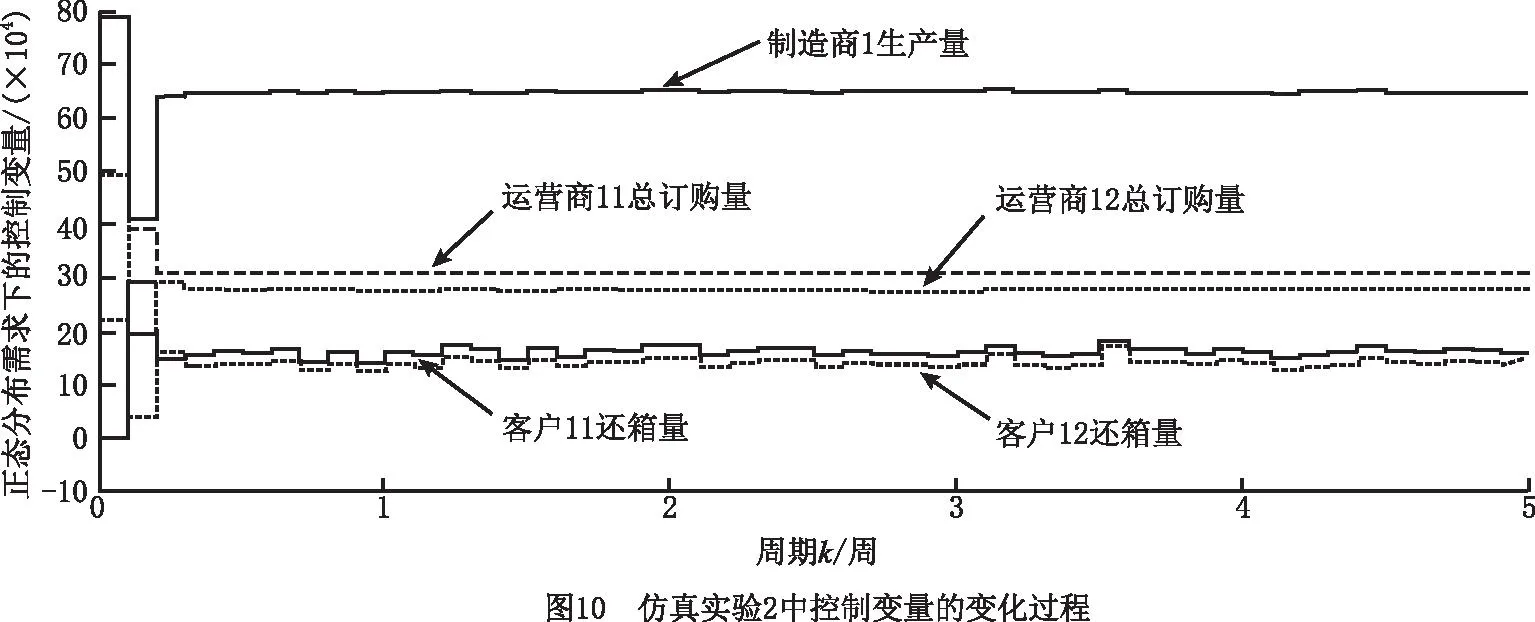
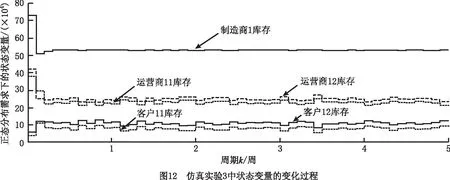
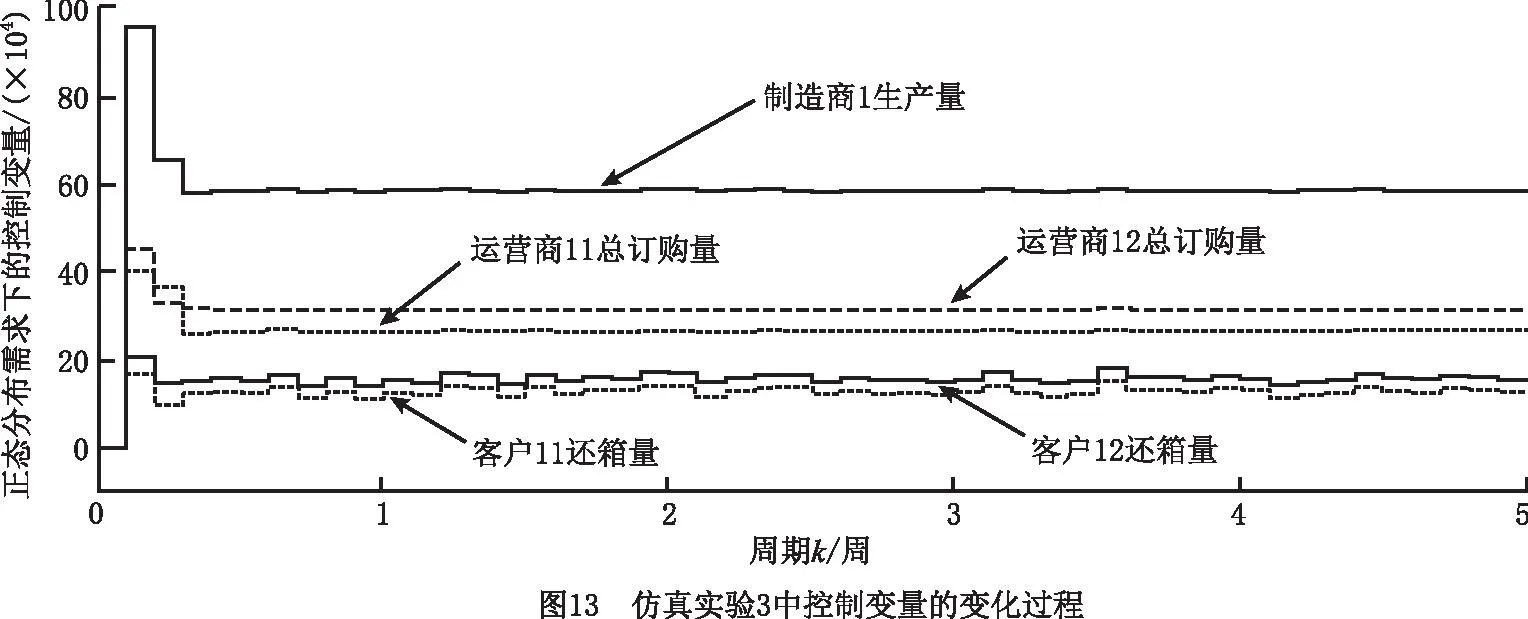
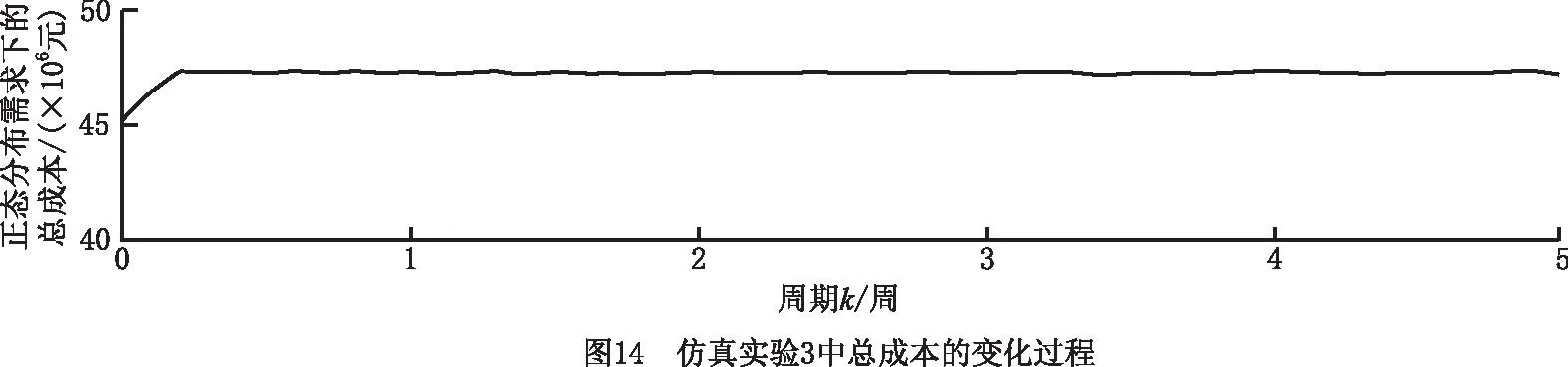
(3)仿真实验3 实验结果如图12～图14所示。对于运营商11和运营商12的初始库存均大于各自的期望库存值的情况,为了减少库存积压和库存成本,在系统运作初期,制造商1不生产,而运营商11和运营商12均仅执行供应模式,因此制造商1、运营商11和运营商12的库存迅速减少,客户11和客户12的库存快速增加。当运营商11和运营商12的库存达到各自安全库存值和期望库存值之间时,运营商11和运营商12均开始正常订购模式、供应模式、回收模式、修复模式和废弃模式,系统趋于稳定。

3.2 供应链间的仿真实验

在以下仿真实验中,选择周转箱供应链网络中的制造商1、制造商2、运营商11、运营商21、客户11和客户21为研究对象,则周转箱供应链网络的库存状态转移方程和系统成本转移方程表示为:

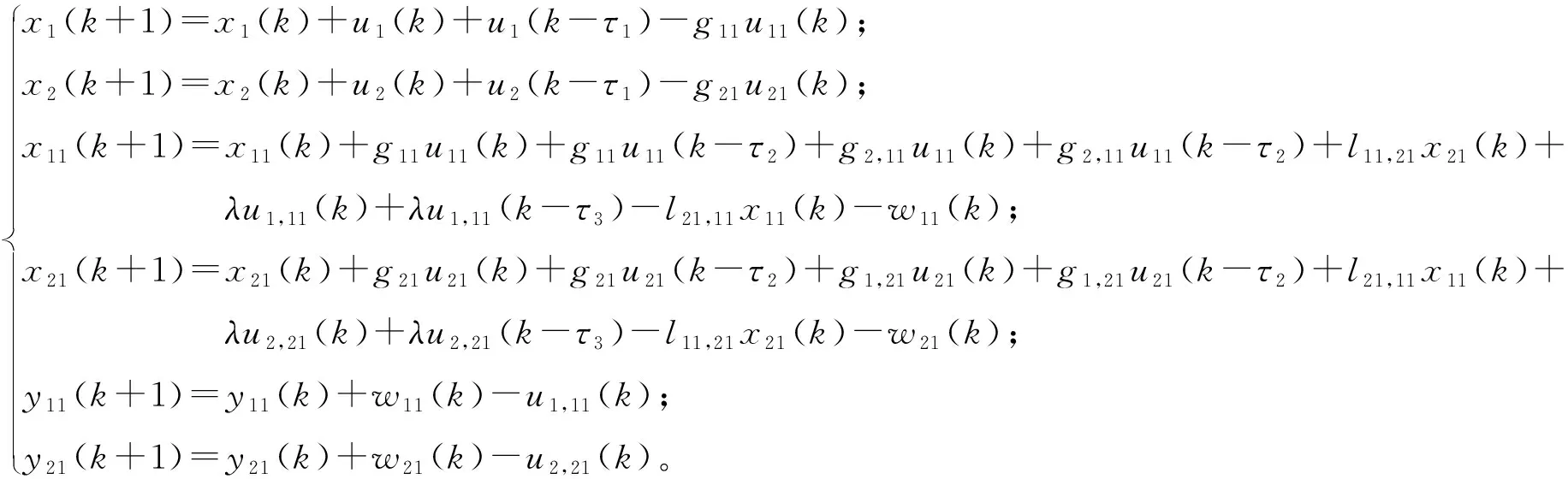
(14)

z(k)=ch1x1(k)+ch2x2(k)+ch11x11(k)+ch21x21(k)+cn1u1(k)+cn1u1(k-τ1)+cn2u2(k)+cn2u2(k-τ1)
+cm11g11u11(k)+cm11g11u11(k-τ2)+cm21g21u21(k)+cm21g21u21(k-τ2)+c′m11g11u11(k)+
c′m11g11u11(k-τ2)+c′m21g21u21(k)+c′m21g21u21(k-τ2)+cm211g2,11u11(k)+cm211g2,11u11(k-τ2)
+cm121g1,21u21(k)+cm121g1,21u21(k-τ2)+cc1121l11,21x21(k)+cc2111l21,11x11(k)+cd11u1,11(k)
+cd11u1,11(k-τ3)+cd21u2,21(k)+cd21u2,21(k-τ3)+cr11λu1,11(k)+cr11λu1,11(k-τ3)+cr21λu2,21(k)
+cr21λu2,21(k-τ3)+co11ηu1,11(k)+co11ηu1,11(k-τ3)+co21ηu2,21(k)+co21ηu2,21(k-τ3)。

(15)

将式(14)和式(15)转化为如下模糊控制系统:

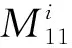
式中:a=1,2,b=1。在不同模糊规则下,系统的参数设置详见附件4。

设计式(16)的状态反馈控制律为:

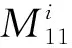
式中:a=1,2,b=1。

因为通过求解定理1中的式(9)和式(10)得到如下正定矩阵,所以式(16)的周转箱供应链网络是鲁棒渐近稳定的。下面将针对表3中3种不同初始值和标称值进行仿真实验。

表3 仿真实验4～仿真实验6的初始值和标称值

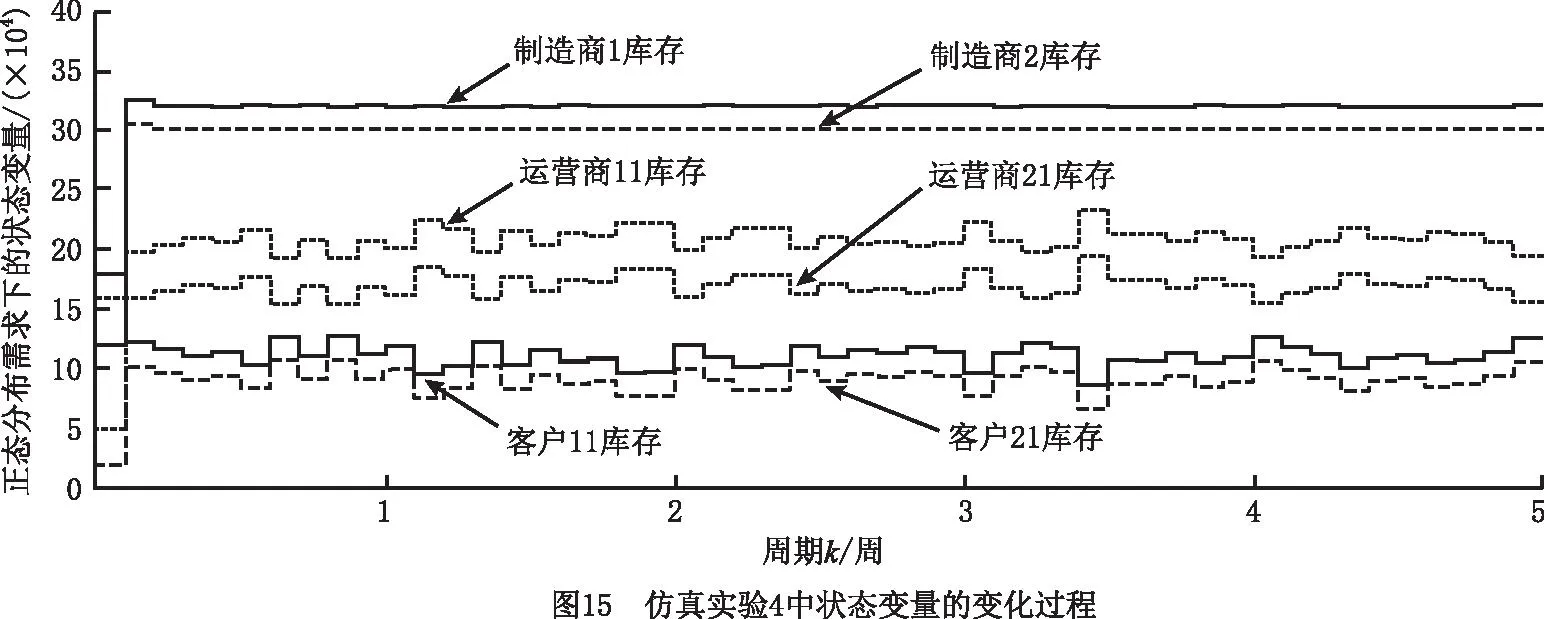
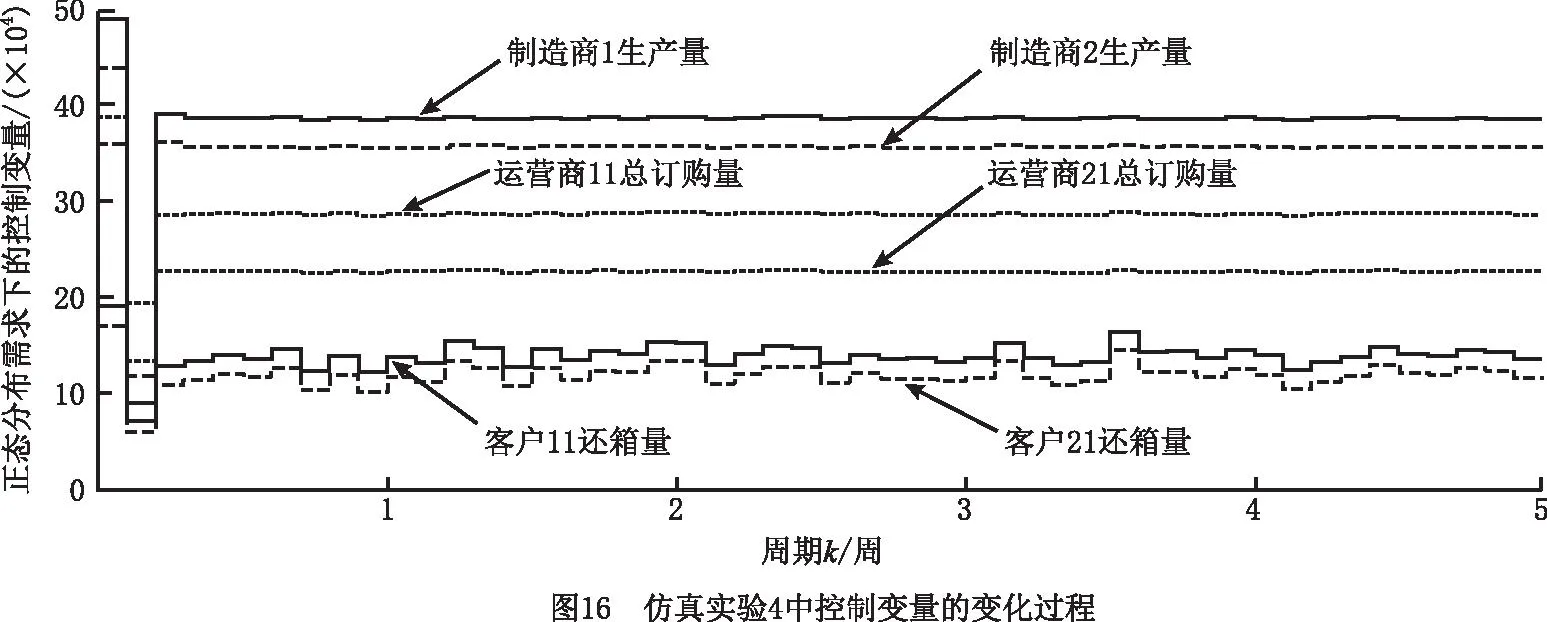
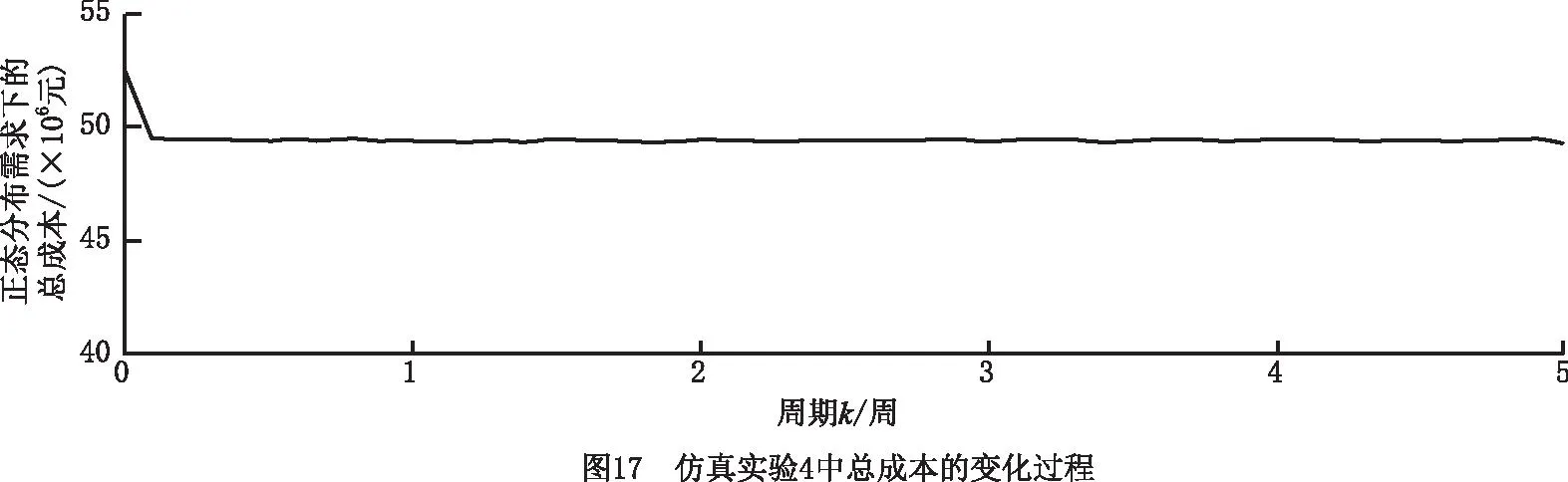
(1)仿真实验4 实验结果如图15～图17所示。对于运营商11和运营商21的初始库存均小于各自安全库存值的情况,为了满足客户需求,在系统运作初期,制造商1和制造商2均执行紧急生产模式,运营商11和运营商21均执行正常订购模式、供应模式、回收模式、修复模式和废弃模式,因此制造商1、运营商11和运营商21的库存迅速增加,而客户11和客户21的库存快速减少。当运营商11和运营商21的库存达到各自安全库存值和期望库存值之间时,制造商1和制造商2执行正常生产模式,而运营商11和运营商21继续保持系统初期的运作模式,且系统各变量均保持稳定运行。

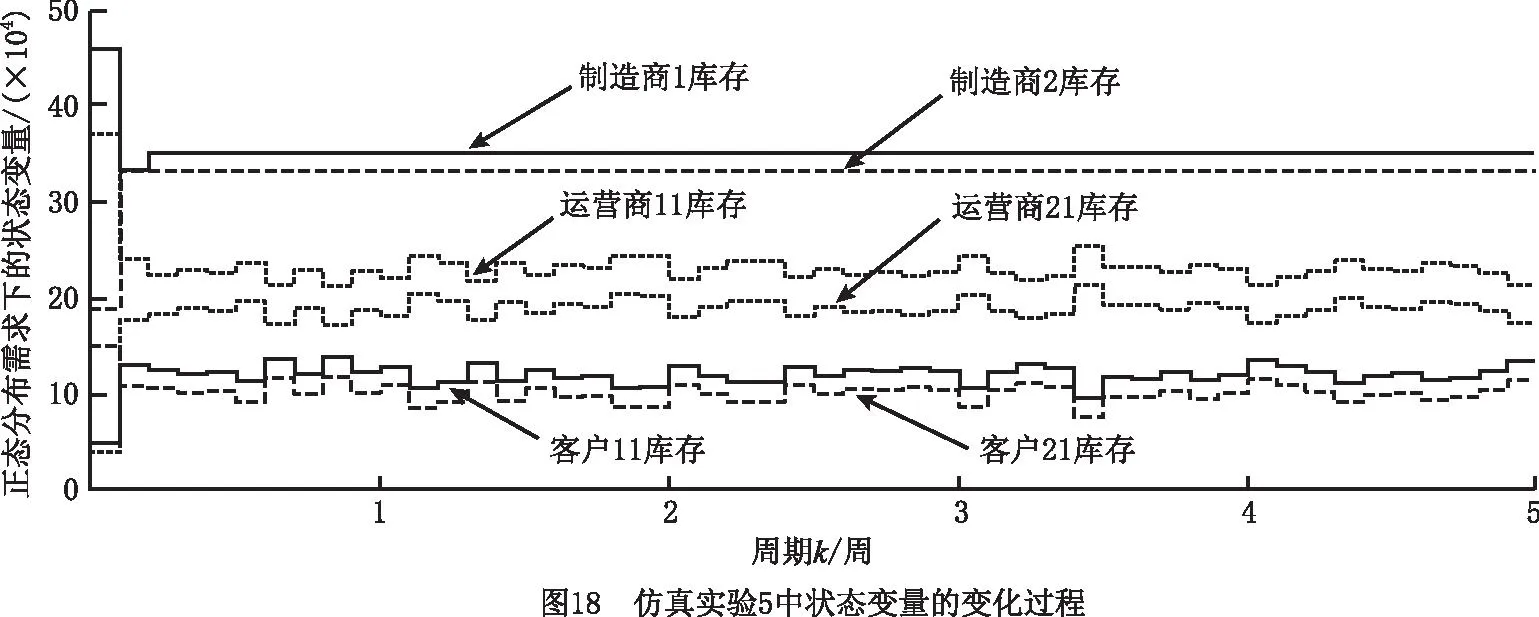
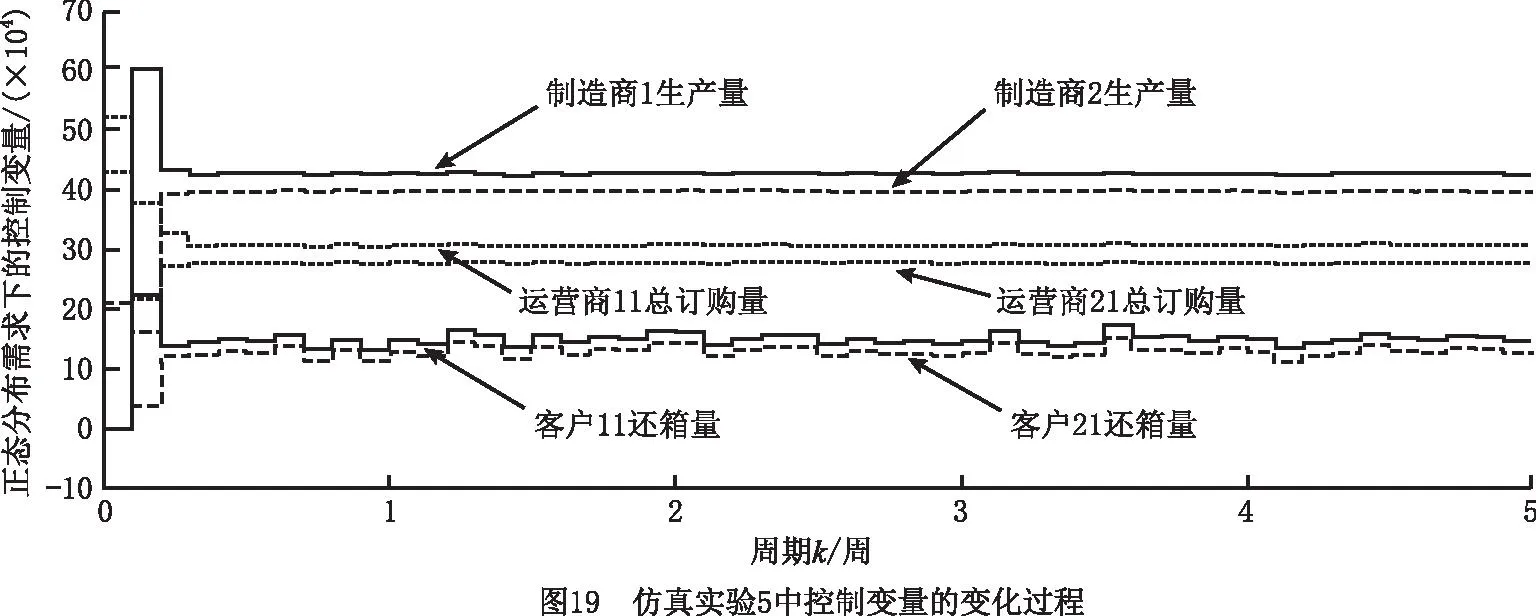
(2)仿真实验5 实验结果如图18～图20所示。对于运营商11初始库存大于其期望库存值,而运营商21的初始库存小于其安全库存值的情况,在系统运作初期,制造商1执行紧急生产模式,制造商2执行正常生产模式,因为运营商11的库存可以满足客户需求,所以其仅执行供应模式和紧急横向转运模式(将周转箱转运至运营商21),运营商21则执行正常订购模式、紧急订购模式、紧急横向转运模式(从运营商11转运周转箱)、供应模式、回收模式、修复模式和废弃模式。在上述模式作用下,制造商1、制造商2、运营商21和客户11的库存迅速增加,运营商11和客户21的库存迅速减少。当运营商11和运营商21的库存达到各自安全库存值和期望库存值之间时,运营商11停止紧急横向转运模式(将周转箱转运至运营商21),并开始正常订购模式、供应模式、回收模式、修复模式和废弃模式,运营商21则停止紧急订购模式和紧急横向转运模式(从运营商11转运周转箱),且系统中的各变量均保持稳定运行。

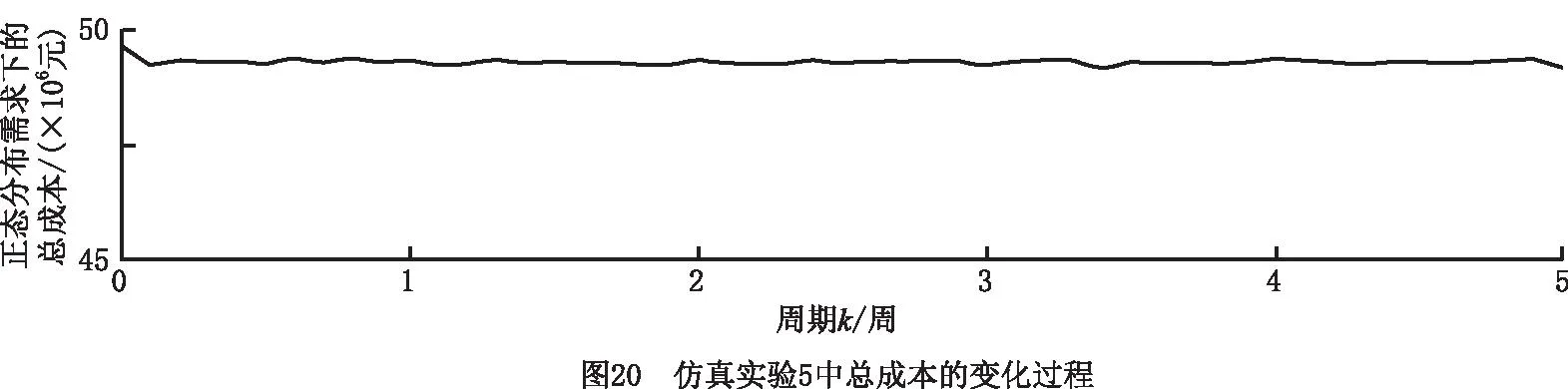
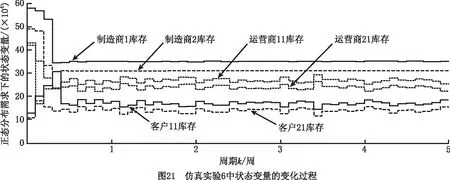
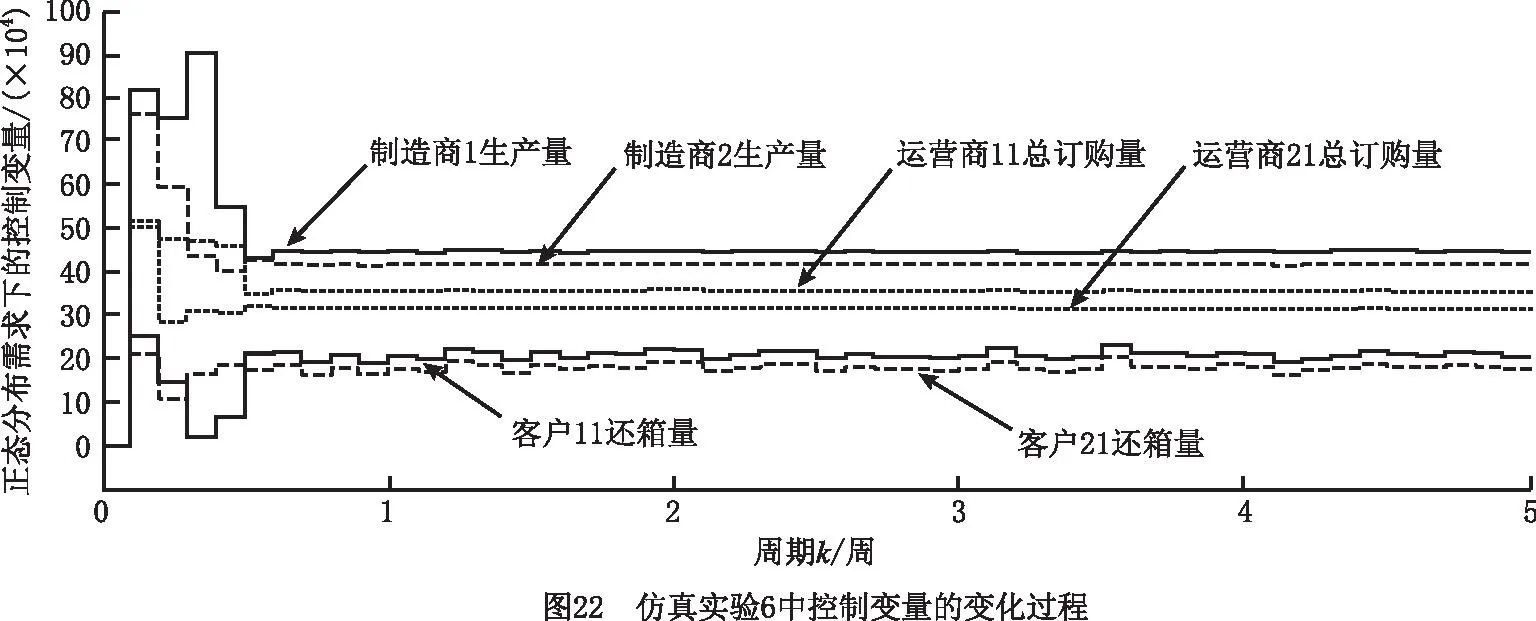
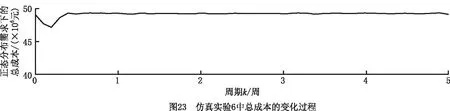
(3)仿真实验6 实验结果如图21～图23所示。对于运营商11和运营商21的初始库存均大于各自期望库存值的情况,为减少库存积压和库存成本,在系统运作初期,制造商1和制造商2不生产,运营商11和运营商21均仅执行供应模式,因此制造商1、制造商2、运营商11和运营商21的库存迅速减少,客户11和客户21的库存迅速增加。当运营商11和运营商21的库存达到各自安全库存值和期望库存值之间时,运营商11和运营商21开始正常订购模式、供应模式、回收模式、修复模式和废弃模式,且系统中的各变量均达到稳定状态。

4 结束语

本文以周转箱多模型系统为研究对象,提出一种降低提前期和不确定需求影响的鲁棒切换策略。在考虑周转箱正向流动中的正常生产模式、紧急生产模式、供应模式和逆向流动中的回收模式、修复模式、废弃模式的基础上,为了充分平衡周转箱供应链各节点企业的周转箱库存以提高周转箱的周转率和降低成本,在链内和链间的上下游之间和同级之间分别设计了正常订购模式、紧急订购模式、正常横向转运模式和紧急横向转运模式。基于以上10种周转箱运作模式,建立了需求不确定下含生产提前期、订购提前期和还箱提前期的周转箱供应链基本模型与周转箱供应链网络基本模型。通过设计制造商的生产切换策略、周转箱供应链内运营商的运作切换策略和周转箱供应链网络中运营商的运作切换策略,将周转箱供应链多模型系统和周转箱供应链网络多模型系统统一表示为Takagi-Sugeno模糊控制系统,并应用模糊控制理论提出一种模糊鲁棒控制策略。通过链内和链间的6个仿真实验表明,无论节点企业的初始库存是低于安全库存、介于安全库存和期望库存之间,还是高于期望库存,在由周转箱的切换策略和鲁棒控制策略组成的周转箱多模型鲁棒切换策略作用下,不但系统的全部变量在经历短暂波动后快速达到鲁棒稳定,而且可以通过切换各种周转箱运作模式实现周转箱供应链和网络低成本运行。由于周转箱供应链网络多模型系统不仅可以在链内运营商间进行正常横向转运模式,还可以在链间运营商间进行紧急横向转运,相比周转箱供应链多模型系统,周转箱供应链网络多模型系统可以进一步提高周转箱的周转率、平衡运营商之间的周转箱库存和降低系统的运作成本。本文提出的周转箱多模型系统及其鲁棒切换策略也可以应用到托盘等物流单元器具的系统中。下一步的研究方向为VUCA(volatility,uncertainty,complexity,ambiguity)时代下物流单元器具多模型系统韧性的提升。

附录

1 周转箱供应链多模型系统中的向量和系统矩阵表达式

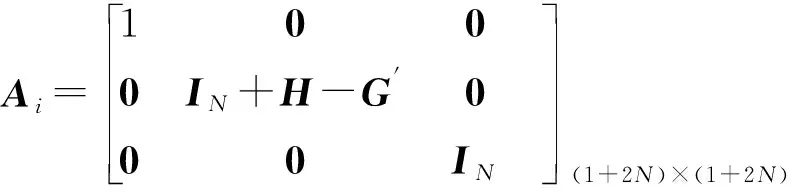
将附录1各向量和参数矩阵表达式中的a修改为a=1,2,…,M,并增加紧急横向转运下的库存状态系数矩阵和成本系数矩阵,即可得到式(6)中各向量和参数矩阵的表达式。

2 仿真实验的通用参数设置

ch1=ch2=0.002,ch11=ch12=ch21=0.002 7,cn1=cn2=0.042,cm11=cm12=cm21=0.055,cc112=cc121=0.057,c′m11=c′m21=0.059,cc1121=cc2111=0.06,cm211=cm212=cm121=0.061,cd11=cd12=cd21=0.002,cr11=cr12=cr21=0.02,co11=co12=co21=0.002(×103元),λ=0.95,η=0.05,γ=0.68,w11(k)=w12(k)=w21(k)～N(6,12)。

3 供应链内仿真实验的参数设置

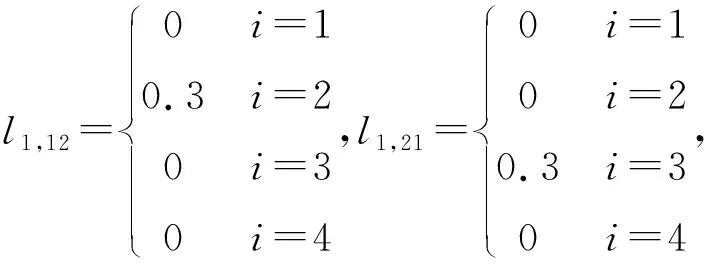
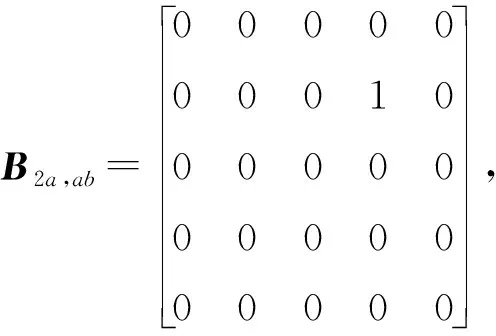
B4=0,B4a=0,B4ab=0,

D4a,ab=0,a=1,b=1,2。

4 供应链网络仿真实验的参数设置

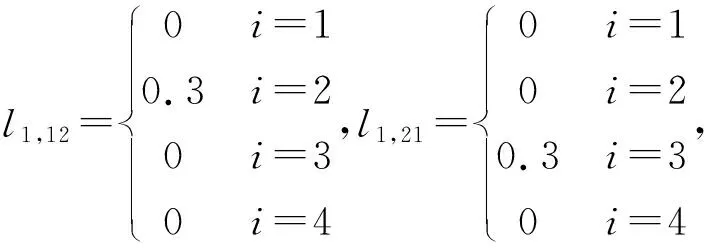
B4=0,B4a=0,B4ab=0,B4a,ab=0,

D4=0,

D4a,ab=0,a=1,2,b=1。