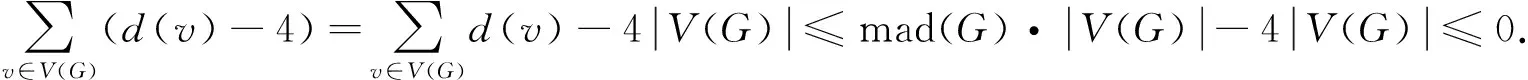稀疏图平方图的染色数上界

张 艳

(天津大学 应用数学中心, 天津 300072)

1 引言与主要结果

本文所考虑的图均为有限的简单无向图.对于一个图G, 用E(G),V(G)和Δ(G)分别表示图G的边集、顶点集和最大度.用d-点、d--点和d+-点分别表示度数为d的点、度数不大于d的点和度数不小于d的点.图G的k-顶点染色是指映射c:V(G)→{1,2,…,k}; 如果当u～v时, 有c(u)≠c(v), 则称染色c是正常的[1].图G的平方G2定义为: 顶点集V(G)=V(G2), 并且uv∈E(G2)当且仅当u和v之间的距离至多为2.平方图G2的色数是指使得G2存在正常k-染色的最小整数k, 用χ(G2)表示.根据定义, 有χ(G2)≥Δ(G)+1, 其中Δ(G)是指图G的最大度[2].文献[3]研究了平面图的相关性质.

猜想1[4]如果G是一个平面图, 则:

1) 当Δ(G)=3时, 有χ(G2)≤7;

2) 当4≤Δ(G)≤7时, 有χ(G2)≤Δ(G)+5;

Wegner[4]证明了如果猜想1是正确的, 则χ(G2)的上界是紧的, 并且如果Δ(G)=3, 则χ(G2)≤8.对于超平面图, 文献[5]证明了猜想1.但在平面图中, 该猜想未得到验证.

图G的最大平均度定义如下:

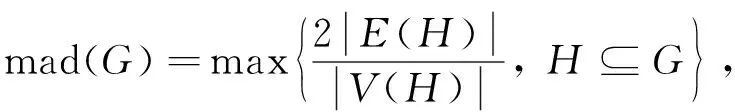
(1)

其中V(H)和E(H)分别指子图H的顶点集和边集.

定理2[7]设图G的最大度Δ(G)=Δ, 则有如下结论:

2) 如果mad(G)<3,Δ≠5, 则χ(G2)≤Δ+5; 如果mad(G)<3,Δ=5, 则χ(G2)≤11;

Charpentier猜想[8]: 如果mad(G)<4, 则χ(G2)≤2Δ(G).文献[9]通过构造图G, 使得图G满足mad(G)<4, 而χ(G2)=2Δ(G)+2, 进而否定了Charpentier猜想.此外, Charpentier[8]还证明了对于充分大的Δ(G), 如果mad(G)<4, 则χ(G2)≤3Δ(G)+3.因此, 有

2Δ(G)+2≤max{χ(G2)|mad(G)<4}≤3Δ(G)+3.

(2)

定理3[8]如果mad(G)<4并且Δ(G)≥8, 则χ(G2)≤3Δ(G)+1.

对于最大度Δ(G)≤5的图,χ(G2)的上界为3Δ(G)+1, 并且该上界是紧的[8].

定义1在图G中, 若存在一个顶点的排序σ:v1,v2,…,vn, 使得对任意的vi(2≤i≤n), |vj:vi～vj,j

本文主要结果如下:

定理4如果mad(G)<4且Δ(G)≥7, 则χ(G2)≤3Δ(G)+1.

定理5如果mad(G)≤4且Δ(G)≥8, 则χ(G2)≤3Δ(G)+5.

2 定理4的证明

要证明定理4, 只需证明对任意的图G满足mad(G)<4且Δ≥7时,G2是3Δ-退化的即可.用反证法, 假设图G是满足mad(G)<4且Δ≥7边数最少的极小反例,G2不是3Δ-退化的.先令G中每个顶点的初始权重为w(v)=d(v)-4, 由于mad(G)<4, 因而初始总权重为负; 然后利用权转移规则, 将顶点间的权重进行相互转移, 计算经过权重转移后的总权重, 如果是非负的, 则得矛盾.在每个顶点权重转移过程中, 需找出在图G中所规避的构型.

2.1 相关命题

定义2设v是图G的d点, 用di(v)表示点v在图G中i邻域的个数(i=2,3).当d(v)≥4时, 对顶点定义如下:

1) 如果d(v)-d2(v)≥7, 则v是好顶点.

2) 如果d(v)-d2(v)=6, 则v是弱好顶点.

3) 如果d(v)-d2(v)=5, 则v是A型弱坏顶点.当d3(v)=0时,v称为A型第一类的; 当1≤d3(v)≤3时,v称为A型第二类的.

4) 如果d(v)-d2(v)=4, 则v是B型弱坏顶点.当d3(v)=0时,v称为B型第一类的; 当d3(v)=1时,v称为B型第二类的.

5) 如果d(v)-d2(v)=3, 则v是坏顶点.

首先假设图G是极小反例, 即图G满足mad(G)<4并且Δ≥7, 但G2不是3Δ-退化的.根据图G的极小性, 在图G中删除某条uv边后(Guv)2是3Δ-退化的, 最后只需证明G2是3Δ-退化的, 得矛盾.

命题1图G中的每个4+-顶点都是定义2中的一种.

证明: 假设G中的顶点v既不是坏顶点, 也不是B型弱坏顶点、A型弱坏顶点、弱好顶点和好顶点, 则根据定义有d(v)-d2(v)≤2, 或者d(v)-d2(v)=4并且d3(v)≥2, 或者d(v)-d2(v)=5并且d3(v)≥4.

对于第一种情形, 因为d(v)≥4, 所以v有2邻域, 记为w.根据图G的极小性, (Gvw)2是3Δ-退化的.假设σ是(Gvw)2的好排序, 可先从σ中删除v及v的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前出现的邻域个数至多为2Δ+Δ-2=3Δ-2.对于每个2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.

对于第二种情形, 令w1,w2分别是v的两个3邻域.根据图G的极小性, (Gvw1)2是3Δ-退化的.假设σ是(Gvw1)2的好排序, 可做如下操作: 先从σ中删除v,w1,w2及v的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前且与其相邻的顶点个数至多为2Δ+Δ-4+4=3Δ.对于wi(i=1,2), 出现在其之前且与其相邻的顶点至多有(2Δ+4)个.最后对于2顶点, 与之相邻且出现在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.

对于第三种情形, 令w1,w2,w3,w4分别是v的3邻域.根据图G的极小性, (Gvw1)2是3Δ-退化的.假设σ是(Gvw1)2的好排序, 可做如下操作： 先从σ中删除v,w1,w2,w3,w4及v的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前且与其相邻的顶点个数至多为Δ+Δ-5+8=2Δ+3.对于wi(i=1,2,3,4), 与其相邻且出现在其之前的顶点个数至多为2Δ+5.最后对于2顶点, 与其相邻且出现在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.证毕.

命题2在图G中, 3--点不与3--点相邻.

证明: 设u,v是图G中两个相邻的3--点.根据图G的极小性, (Guv)2是3Δ-退化的.假设σ是(Guv)2的好排序, 可先从σ中删除u和v, 形成新的排序σ′, 然后在σ′中将u和v依次加回.显然, 与u相邻并且排在u前面的顶点个数至多为2Δ+3,v同理.因此G2是3Δ-退化的, 矛盾.证毕.

命题3在图G中, 坏顶点不与3点相邻, 并且其4+邻域点不是坏顶点.

证明： 设v是图G的坏顶点,u是与v相邻的3顶点.根据图G的极小性, (Gvu)2是3Δ-退化的.假设σ是(Gvu)2的好排序, 可先从σ中删除v和u及v所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回来.首先对于点v, 出现在点v之前且与其相邻的顶点个数至多为2Δ+Δ-3+2=3Δ-1.对于点u, 排在其之前的邻域至多有(2Δ+3)个.最后对于2顶点, 排在其之前且与其相邻的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.

假设x是图G的坏顶点, 并且x是v的4+邻域点,w是v的2邻域.根据图G的极小性, (Gvw)2是3Δ-退化的.假设σ是(Gvw)2的好排序, 可先从σ中删除v及v和x所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前且与其相邻的顶点个数至多为2Δ+Δ-3+3=3Δ.对于(2Δ-6)个2邻域的每个点, 与之相邻且排在其之前的顶点个数至多为Δ+4+2Δ-6=3Δ-2.因此G2是3Δ-退化的, 矛盾.证毕.

命题4如果v是图G中B型弱坏顶点u的坏邻域, 则v至少有2个好邻域.

证明: 假设w(w≠u)是v的邻域, 并且w不是好顶点.因为v是坏邻域, 所以v有2邻域x.根据图G的极小性, (Gvx)2是3Δ-退化的.假设σ是(Gvx)2的好排序, 可先从σ中删除点v及v和w所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.首先对于点v, 与点v相邻并且排在之前的顶点个数至多为

Δ-3+4+Δ+d(w)-d2(w)=2Δ+1+d(w)-d2(w)≤2Δ+7

(因为w不是好顶点, 所以d(w)-d2(w)≤6).此外, 与2顶点相邻且排在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.证毕.

命题5在图G中, 每个B型第一类的弱坏顶点至多有2个坏邻域.

证明: 设u是B型第一类的弱坏顶点, 假设u至少有3个坏邻域, 记为v1,v2,v3.由图G的极小性, (Guv1)2是3Δ-退化的.假设σ是(Guv1)2的好排序, 可先从σ中删除u,v1,v2,v3及其所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于vi(i=1,2,3), 排在vi之前且与其相邻的顶点个数至多为2Δ+Δ-3+3=3Δ.对于点u, 与之相邻且排在之前的顶点个数至多为Δ-4+Δ+3×3=2Δ+5.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.证毕.

命题6在图G中, 没有好邻域但有坏邻域的B型第一类弱坏顶点至少有1个弱好邻域.

证明: 设u是没有好邻域但有坏邻域的B型第一类弱坏顶点, 且u没有弱好邻域, 记其中的1个坏邻域为v1, 其他邻域为v2,v3,v4.由图G的极小性, (Guv1)2是3Δ-退化的.假设σ是(Guv1)2的好排序, 可做如下操作: 先从σ中删除u,v1及u,v1,v2,v3,v4所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.首先对于v1, 排在其之前且与其相邻的顶点个数至多为2Δ+Δ-3+3=3Δ.对于点u, 与u相邻且排在其之前的顶点个数至多为

(因为vi(i=2,3,4)既不是好邻域也不是弱好邻域, 所以d(vi)-d2(vi)≤5).最后对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.证毕.

命题7每个B型第二类的弱坏顶点至多有1个坏邻域.

证明: 设u是B型第二类的弱坏顶点, 且u至少有2个坏邻域, 记为v1和v2, 令w是u的3邻域.由图G的极小性, (Guw)2是3Δ-退化的.假设σ是(Guw)2的好排序, 可做如下操作： 先从σ中删除u和w及u,v1,v2所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.首先对于点u, 与u相邻且排在其之前的顶点个数至多为Δ-4+Δ+2×3+2=2Δ+4.其次, 对于3顶点w, 与w相邻且排在其之前的顶点至多有(2Δ+4)个.最后对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.证毕.

命题8在图G中, 没有好邻域的B型第二类弱坏顶点至少有2个弱好邻域; 有坏邻域且仅有1个好邻域的B型第二类弱坏顶点至少有1个弱好邻域.

证明: 设u是图G中没有好邻域的B型第二类弱坏顶点, 且u至多有1个弱好邻域.令w是u的3邻域, 其他邻域为vi(i=1,2,3).由图G的极小性, (Guw)2是3Δ-退化的.假设σ是(Guw)2的好排序, 可做如下操作: 先从σ中删除u和w及u,v1,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.如果u有1个弱好邻域, 记为v1, 则与u相邻且排在u之前的顶点个数至多为

Δ-2+d(v1)-d2(v1)+d(v2)-d2(v2)+d(v3)-d2(v3)≤Δ-2+6+2×5=Δ+14

(因为vi(i=2,3)既不是好邻域也不是弱好邻域, 所以d(vi)-d2(vi)≤5); 如果u没有弱好邻域, 则与u相邻且排在其之前的顶点个数至多为

Δ-2+d(v1)-d2(v1)+d(v2)-d2(v2)+d(v3)-d2(v3)≤Δ-2+5×3=Δ+13

(因为vi(i=1,2,3)既不是好邻域也不是弱好邻域, 所以d(vi)-d2(vi)≤5).此外, 对于3顶点w, 与w相邻且排在其之前的顶点至多有(2Δ+4)个.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.

同理, 设u′是图G中有坏邻域且仅有1个好邻域的B型第二类弱坏顶点, 且u′不存在弱好邻域.令w′是u′的3邻域, 其他邻域为其中是u′唯一的好邻域,是u′的坏邻域.因为u′不存在弱好邻域, 所以既不是好顶点也不是弱好顶点.由图G的极小性, (Gu′w′)2是3Δ-退化的.假设σ是(Gu′w′)2的好排序, 可做如下操作： 先从σ中删除u′和w′及所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u′, 与u′相邻且排在其之前的顶点个数至多为

命题9在图G中, 设A型第一类弱坏顶点为u, 且其邻域为vi(i=1,2,3,4,5).令a=|{vi:vi是有2个好邻域的坏顶点}|,b=|{vi:vi是至多有1个好邻域的坏顶点}|, 则有以下几种情形:

1) 当a=0时,b≤3;

2) 当a=1时,b≤2;

3) 当a=2时,b≤2;

4) 当a=3时,b≤1.

证明: 1) 当a=0时, 假设b≥4, 令至多有1个好邻域的坏顶点分别为v1,v2,v3,v4, 并且u与vi(i=1,2,3,4)相邻.根据图G的极小性, (Guv1)2是3Δ-退化的.假设σ是(Guv1)2的好排序, 可先从σ中删除u,v1,v2,v3,v4及其所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.因为vi(i=1,2,3,4)是至多有1个好邻域的坏顶点, 所以vi存在不是好顶点的邻域, 记为zi.在寻找与vi相邻且排在其之前顶点的个数时需删除zi的2邻域.在σ′中, 与vi相邻且排在其之前的顶点个数至多为

Δ-3+4+Δ+d(zi)-d2(zi)≤2Δ+1+6=2Δ+7≤3Δ

(因为zi不是好顶点, 所以d(zi)-d2(zi)≤6).对于点u, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+4×3=2Δ+7.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是3Δ-退化的, 矛盾.

2) 当a=1时, 假设b≥3, 令有2个好邻域的坏顶点为v1, 至多有1个好邻域的坏顶点为v2,v3,v4, 并且u与vi(i=1,2,3,4)相邻.根据图G的极小性, (Guv2)2是3Δ-退化的.假设σ是(Guv2)2的好排序, 可先从σ中删除u,v2,v3,v4及其与v1所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.因为vi(i=2,3,4)是至多有1个好邻域的坏顶点, 与第一种情形类似.对于u, 在σ′中, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+4×3=2Δ+7.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.

3) 当a=2时, 假设b≥3, 令有2个好邻域的坏顶点为v1和v2, 至多有1个好邻域的坏顶点为v3,v4,v5, 并且u与vi(i=1,2,3,4,5)相邻.根据图G的极小性,(Guv3)2是3Δ-退化的.假设σ是(Guv3)2的好排序, 可先从σ中删除u,v3,v4,v5及其与v1,v2所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.因为vi(i=3,4,5)是至多有一个好邻域的坏顶点, 与第一种情形类似.在σ′中, 对于u, 与u相邻且排在其之前的顶点个数至多为Δ-5+5×3=Δ+10.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.

4) 当a=3时, 假设b=2, 令有2个好邻域的坏顶点为v1,v2,v3, 至多有1个好邻域的坏顶点为v4和v5, 并且u与vi(i=1,2,3,4,5)相邻.根据图G的极小性, (Guv4)2是3Δ-退化的.假设σ是(Guv4)2的好排序, 可先从σ中删除u,v4,v5及其与v1,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.因为vi(i=4,5)是至多有1个好邻域的坏顶点, 与第一种情形类似.在σ′中, 对于u, 与u相邻且排在其之前的顶点个数至多为Δ-5+5×3=Δ+10.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.证毕.

命题10设u是图G中A型第二类的弱坏顶点, 当d3(u)=1时,u至多有2个坏邻域; 当d3(u)=2时,u至多有一个坏邻域; 当d3(u)=3时,u没有坏邻域.

证明: 当d3(u)=1时, 假设u至少有3个坏邻域v1,v2,v3, 且u的3邻域为x.根据图G的极小性, (Gux)2是3Δ-退化的.假设σ是(Gux)2的好排序, 可先从σ中删除u和x及u,v1,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于u, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+3×3+2=2Δ+6.对于3度顶点x, 与之相邻且排在其之前的顶点至多有(2Δ+5)个.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.

当d3(u)=2时, 假设u至少有2个坏邻域v1,v2, 且u的2个3邻域分别为w1和w2.根据图G的极小性, (Guw1)2是3Δ-退化的.假设σ是(Guw1)2的好排序, 可先从σ中删除u,w1,w2及u,v1,v2所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于u, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+2×3+2×2=2Δ+5.对于wi(i=1,2), 与之相邻且排在其之前的顶点至多有(2Δ+5)个.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.

当d3(u)=3时, 假设u存在坏邻域v1, 令u的3邻域分别为w1,w2,w3.根据图G的极小性, (Guw1)2是3Δ-退化的.假设σ是(Guw1)2的好排序, 可先从σ中删除u,w1,w2,w3及u和v1所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于u, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+3+2×3=2Δ+4.对于wi(i=1,2,3), 与之相邻且排在其之前的顶点至多有(2Δ+5)个.最后对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是3Δ-退化的, 矛盾.证毕.

2.2 权转移规则

因为mad(G)<4, 所以有

(3)

令每个顶点的初始权重为w(v)=d(v)-4, 易知图G的初始总权重是负的.下面制定一些权重转移规则, 使得顶点间经过权重转移后, 图G中每个顶点的权重是非负的, 进而图G的总权重是非负的, 形成矛盾.

下面计算经过权重转移后各顶点的最终权重.

2.2.1 3--点 根据权转移规则1,G中的每个2顶点会从其每个邻域接收1的权重, 而且不会失去任何权重, 因此其最终权重是w′(v)=2-4+2×1=0.

2.2.2 坏顶点 令v是图G的坏顶点, 根据权转移规则1,v将权重给相邻的2邻域后,v的剩余权重为-1.此外, 注意到坏顶点不是好顶点和弱好顶点, 根据命题3,v不与3点相邻并且v没有坏邻域, 因此v不会再失去任何权重.

2.2.3B型弱坏顶点 令v是图G的B型弱坏顶点.

1) 如果v是B型第一类的, 则根据权转移规则1,v将权重给相邻的2邻域后,v的剩余权重是0.如果v没有坏邻域, 则v不会再失去任何权重,v的权重是非负的; 如果v有坏邻域, 则根据命题4和命题5,v至多有2个坏邻域, 而且这2个坏邻域都至少有2个好邻域, 由权转移规则4,v最多再失去的权重.此时, 若v有好邻域, 则根据权转移规则5,v会接收来自好邻域的权重, 因此其最终权重是非负的.否则,v没有好邻域但v有坏邻域, 根据命题6,v至少有一个弱好邻域, 由权转移规则6,v会接收来自弱好邻域的权重, 因此其最终权重也是非负的.

2) 如果v是B型第二类的, 则根据权转移规则1,v将权重给相邻的2邻域和3邻域后, 其剩余权重是如果v没有坏邻域, 此时若v有好邻域, 由权转移规则5,v接收来自好邻域的权重, 则v的最终权重是非负的; 否则v没有好邻域, 根据命题8,v至少有2个弱好邻域, 再根据权转移规则6,v会接收来自弱好邻域的权重, 因此v的最终权重也是非负的; 如果v有坏邻域, 则根据命题4和命题7,v至多有1个坏邻域, 而且这个坏邻域至少有2个好邻域, 由权转移规则4,v最多需给坏邻域的权重.此时, 若v至少有2个好邻域, 则根据权转移规则5,v接收来自好邻域的权重, 因此v的最终权重是非负的.否则, 若v有1个好邻域且v有坏邻域, 则根据命题8及权转移规则5,6,v至少有1个弱好邻域, 因此v会分别接收来自好邻域的权重及弱好邻域的权重,v的最终权重是非负的; 若v没有好邻域, 则根据命题8,v至少有2个弱好邻域, 由权转移规则6, 其会接收来自弱好邻域的权重, 因此其最终权重仍是非负的.

2.2.4A型弱坏顶点 令v是图G的A型弱坏顶点.

1) 如果v是A型第一类的, 则根据权转移规则1,v将权重给相邻的2邻域后, 其剩余权重是1.令

a=|{vi:vi～v, 且vi是有2个好邻域的坏顶点}|,

b=|{vi:vi～v, 且vi是至多有1个好邻域的坏顶点}|.

2) 如果v是A型第二类的, 则当d3(v)=1时, 根据权转移规则1,v将权重给相邻的2邻域和3邻域后, 其剩余权重是根据命题10,v至多有2个坏邻域, 再由权转移规则3,4,v最多会失去的权重, 因此其最终权重是非负的; 当d3(v)=2时, 根据权转移规则1,v将权重给相邻的2邻域和3邻域后, 其剩余权重是根据命题10,v至多有1个坏邻域, 再由权转移规则3,4,v最多会失去的权重, 因此其最终权重是非负的; 当d3(v)=3时, 根据权转移规则1,v将权重给相邻的2邻域和3邻域后, 其剩余权重是0.根据命题10,v没有坏邻域, 不会再失去权重, 因此v的最终权重为0.

综上可见,v的最终权重是非负的.

2.2.5 弱好顶点 令v是图G的弱好顶点.根据权转移规则1,v将权重给相邻的2邻域后, 此时v的剩余权重为2.因为v不是好顶点, 根据权转移规则1,3,4,6, 所以v会将权重给3邻域、坏邻域及与之相邻的B型弱坏顶点.因为d(v)-d2(v)=6, 所以v至多会失去的权重, 因此v的最终权重是非负的.

2.2.6 好顶点 令v是图G的好顶点, 且记d2(v)是v的2邻域的个数.根据权转移规则1,2,3,5, 因为v是好顶点, 所以至多有(d(v)-d2(v))个邻域分别会接收来自v的至多的权重, 因此其最终权重为

(因为d(v)-d2(v)≥7).

通过上述对顶点间的权重转移, 可得图G中每个顶点的最终权重为非负的, 因此图G的最终总权重也是非负的, 与初始总权重是负的矛盾.

3 定理5的证明

定理5的证明类似定理4, 需找出在图G中规避的构型.

3.1 相关命题

定义3设v是图G的d点, 用di(v)表示点v在图G中i邻域的个数(i=2,3,4).当d(v)≥5时, 对顶点定义如下:

1) 如果d(v)-d2(v)≥8, 则v是优顶点.

2) 如果d(v)-d2(v)≥7, 则v是好顶点.

3) 如果d(v)-d2(v)=6, 则v是弱好顶点.

4) 如果d(v)-d2(v)=5, 则v是A型弱坏顶点.当d3(v)=0时,v称为A型第一类的; 当1≤d3(v)≤2时,v称为A型第二类的.

5) 如果d(v)-d2(v)=4, 则v是B型弱坏顶点.当d3(v)=0时,v称为B型第一类的; 当d3(v)=1时,v称为B型第二类的.

6) 如果d(v)-d2(v)=3, 则v是坏顶点.

首先假设图G是极小反例, 即图G满足mad(G)≤4且Δ≥8, 但G2不是(3Δ+4)-退化的.根据图G的极小性, 在图G中删除某条uv边后(Guv)2是(3Δ+4)-退化的, 最后只需证明G2是(3Δ+4)-退化的, 得到矛盾.

命题11图G中的每个5+-顶点都是定义3中的一种.

证明: 假设图G中的顶点v既不是坏顶点, 也不是A型弱坏顶点、B型弱坏顶点、弱好顶点和好顶点, 则根据定义有d(v)-d2(v)≤2, 或者d(v)-d2(v)=4并且d3(v)≥2, 或者d(v)-d2(v)=5并且d3(v)≥3.

对于第一种情形, 因为d(v)≥5, 所以v有2° 邻域, 记为w.根据图G的极小性, (Gvw)2是(3Δ+4)-退化的.假设σ是(Gvw)2的好排序, 可先从σ中删除v及v的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前出现的邻域个数至多为2Δ+Δ-2=3Δ-2.对于每个2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.

对于第二种情形, 令w1,w2分别是v的2个3邻域.根据图G的极小性, (Gvw1)2是(3Δ+4)-退化的.假设σ是(Gvw1)2的好排序, 可先从σ中删除v,w1,w2及v的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前且与其相邻的顶点个数至多为2Δ+Δ-4+4=3Δ.对于wi(i=1,2), 排在其之前且与其相邻的顶点个数至多为2Δ+4.对于2顶点, 与之相邻且出现在其之前的顶点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.

对于第三种情形, 令w1,w2,w3分别是v的3邻域.根据图G的极小性, (Gvw1)2是(3Δ+4)-退化的.假设σ是(Gvw1)2的好排序, 可先从σ中删除v,w1,w2,w3及v的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 出现在点v之前且与其相邻的顶点个数至多为2Δ+Δ-5+6=3Δ+1.对于wi(i=1,2,3), 出现在其之前的邻域个数至多为2Δ+5.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题12在图G中, 4--点不与4--点相邻.

证明: 设u,v是图G中两个相邻的4--顶点.根据图G的极小性, (Guv)2是(3Δ+4)-退化的.假设σ是(Guv)2的好排序, 可先从σ中删除u和v, 形成新的排序σ′, 然后在σ′中将u和v依次加回.显然, 对于点u, 与u相邻并且排在其之前的顶点至多有(3Δ+4)个,v同理.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题13在图G中, 坏顶点v既不与3点相邻也不与4点相邻, 并且v的5+邻域点不是坏顶点.

证明: 设u是与v相邻的3顶点.根据图G的极小性, (Gvu)2是(3Δ+4)-退化的.假设σ是(Gvu)2的好排序, 可先从σ中删除v和u及v所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 出现在v之前且与其相邻的顶点个数至多为2Δ+Δ-3+2=3Δ-1.对于3点u, 排在u之前的邻域至多有(2Δ+3)个.对于2顶点, 排在其之前且与其相邻的点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.

设w是与v相邻的4顶点.根据图G的极小性, (Gvw)2是(3Δ+4)-退化的.假设σ是(Gvw)2的好排序, 可先从σ中删除v和w及v所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前且与其相邻的顶点个数至多为2Δ+Δ-3+3=3Δ.对于4点w, 排在w之前的邻域至多有(3Δ+3)个.对于2顶点, 排在其之前且与其相邻的点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.

假设x是图G中的坏顶点, 并且x是v的5+邻域点,w是v的2邻域.根据图G的极小性, (Gvw)2是(3Δ+4)-退化的.假设σ是(Gvw)2的好排序, 可先从σ中删除v及v和x所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点v, 排在点v之前且与其相邻的顶点个数至多为2Δ+Δ-3+3=3Δ.对于(2Δ-6)个2邻域的每个点, 与之相邻且出现在其之前的顶点个数至多为Δ+4+2Δ-6=3Δ-2.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题14如果v是图G中A型弱坏顶点u的坏邻域, 则v至少有2个优邻域.同理, 若v′是图G中B型弱坏顶点u′的坏邻域, 则v′至少有2个优邻域.

证明: 假设w(w≠u)是v的邻域, 并且w不是优顶点.因为v是坏邻域, 所以v有2邻域x.根据图G的极小性, (Gvx)2是(3Δ+4)-退化的.假设σ是(Gvx)2的好排序, 可先从σ中删除v及v和w所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.首先对于点v, 与v相邻并且排在其之前的顶点个数至多为

Δ-3+5+Δ+d(w)-d2(w)≤ 2Δ+2+7=2Δ+9

(因为w不是优顶点, 所以d(w)-d2(w)≤7).此外, 与2顶点相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.

同理可证v′至少有2个优邻域.证毕.

命题15每个B型第一类的弱坏顶点至多有2个坏邻域.

证明: 设u是B型第一类的弱坏顶点, 且u至少有3个坏邻域, 分别记为v1,v2,v3.因为u是B型第一类弱坏顶点, 所以u有2邻域x, 由图G的极小性, (Gux)2是(3Δ+4)-退化的.假设σ是(Gux)2的好排序, 可先从σ中删除u及u,v1,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u, 与之相邻且排在其之前的顶点个数至多为Δ-4+Δ+3×3=2Δ+5.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题16在图G中, 没有好邻域的B型第一类弱坏顶点至少有1个弱好邻域; 没有好邻域但至少有1个弱好邻域的B型第一类弱坏顶点至多有1个坏邻域.

证明: 设u是没有好邻域的B型第一类弱坏顶点, 且u没有弱好邻域, 其邻域设为v1,v2,v3,v4.因为u是B型第一类弱坏顶点, 所以u有2邻域x, 由图G的极小性, (Gux)2是(3Δ+4)-退化的.假设σ是(Gux)2的好排序, 可先从σ中删除u及u,v1,v2,v3,v4所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u, 与u相邻且排在其之前的顶点个数至多为

(因为vi(i=1,2,3,4)既不是弱好邻域也不是好邻域, 所以d(vi)-d2(vi)≤5).对于2顶点, 与之相邻且排在其之前的点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.

设没有好邻域但至少有1个弱好邻域的B型第一类弱坏顶点为u′, 且其至少有2个坏邻域v1和v2, 其他邻域为z和w, 其中z是弱好邻域.因为u′是B型第一类弱坏顶点, 所以u′有2邻域x′, 由图G的极小性, (Gu′x′)2是(3Δ+4)-退化的.假设σ是(Gu′x′)2的好排序, 可先从σ中删除u′及u′,w,v1,v2,z所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于u′, 与u′相邻且排在其之前的顶点个数至多为

(因为w不是好邻域, 所以d(w)-d2(w)≤6).对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题17在图G中, 每个B型第二类的弱坏顶点u至少有1个好邻域, 此外u至多有1个坏邻域.

证明: 设u没有好邻域, 令w是u的3邻域, 其他邻域为v1,v2,v3.由图G的极小性, (Guw)2是(3Δ+4)-退化的.假设σ是(Guw)2的好排序, 可先从σ中删除u和w及u,v1,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u, 与u相邻且排在其之前的顶点个数至多为

Δ-4+2+d(v1)-d2(v1)+d(v2)-d2(v2)+d(v3)-d2(v3)≤Δ-2+6×3=Δ+16

(因为vi(i=1,2,3)不是好顶点, 所以d(vi)-d2(vi)≤6).此外, 对于3顶点w, 与w相邻且排在其之前的顶点至多有(2Δ+4)个.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.

设u至少有2个坏邻域, 记为v1和v2.由图G的极小性, (Guw)2是(3Δ+4)-退化的.假设σ是(Guw)2的好排序, 可先从σ中删除u和w及u,v1,v2所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于u, 与u相邻且排在其之前的顶点个数至多为

Δ-4+2+d(v1)-d2(v1)+d(v2)-d2(v2)+Δ=2Δ+4.

命题18在图G中, 有且仅有1个好邻域的B型第二类弱坏顶点至少有1个弱好邻域.

证明: 设u是有且仅有1个好邻域的B型第二类弱坏顶点, 且u没有弱好邻域, 令w是u的3邻域,v1为u的好邻域, 其他邻域为v2和v3.由图G的极小性, (Guw)2是(3Δ+4)-退化的.假设σ是(Guw)2的好排序, 可先从σ中删除u和w及u,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u, 与u相邻且排在其之前的顶点个数至多为

Δ-4+2+Δ+d(v2)-d2(v2)+d(v3)-d2(v3)≤Δ-2+Δ+2×5=2Δ+8

(因为vi(i=2,3)既不是好邻域又不是弱好邻域, 所以d(vi)-d2(vi)≤5).此外, 对于3顶点w, 与w相邻且排在其之前的顶点至多有(2Δ+4)个.对于2顶点, 与之相邻且排在其之前的顶点至多有2Δ个.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题19在图G中, 每个A型第一类的弱坏顶点至多有4个坏邻域.

证明: 设u是图G中A型第一类的弱坏顶点, 且u至少有5个坏邻域v1,v2,v3,v4,v5.根据图G的极小性, (Guv1)2是(3Δ+4)-退化的.假设σ是(Guv1)2的好排序, 可先从σ中删除u,v1,v2,v3,v4,v5及其所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于vi(i=1,2,3,4,5), 与之相邻且排在其之前的顶点个数至多为2Δ+Δ-3+4=3Δ+1.对于u, 与u相邻且排在其之前的顶点至多有(Δ-5+5×3=Δ+10)个.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题20设u是图G中A型第二类的弱坏顶点, 当d3(u)=1时,u至多有2个坏邻域; 当d3(u)=2时,u至多有1个坏邻域.

证明: 当d3(u)=1时, 假设u至少有3个坏邻域v1,v2,v3, 记u的3邻域为x.根据图G的极小性, (Gux)2是(3Δ+4)-退化的.假设σ是(Gux)2的好排序, 先从σ中删除u和x及u,v1,v2,v3所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+3×3+2=2Δ+6.对于3点x, 与之相邻且排在其之前的顶点至多有(2Δ+5)个.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.

当d3(u)=2时, 假设u至少有2个坏邻域v1,v2, 记u的3邻域分别为w1和w2.根据图G的极小性, (Guw1)2是(3Δ+4)-退化的.假设σ是(Guw1)2的好排序, 先从σ中删除u,w1,w2及u,v1,v2所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于点u, 与u相邻且排在其之前的顶点个数至多为Δ-5+Δ+2×3+2×2=2Δ+5.对于3点wi(i=1,2), 与之相邻且排在其之前的顶点至多有(2Δ+5)个.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.证毕.

命题21设u是图G的弱好顶点, 除u的2邻域外,u的其他邻域有以下几种情形:

1) 若u的邻域中不存在B型弱坏顶点, 则u至多有5个邻域或者是3顶点或者是坏顶点;

2) 若u的邻域中存在1个B型弱坏顶点, 则u至多有4个邻域或者是3顶点或者是坏顶点;

3) 若u的邻域中存在2个B型弱坏顶点, 则u至多有3个邻域或者是3顶点或者是坏顶点;

4) 若u的邻域中存在3个B型弱坏顶点, 则u至多有2个邻域或者是3顶点或者是坏顶点;

5) 若u的邻域中存在4个B型弱坏顶点, 则u至多有1个邻域或者是3顶点或者是坏顶点;

6) 若u的邻域中存在5个B型弱坏顶点, 则u的邻域中不存在3顶点或者是坏顶点.

证明: 1) 若弱好顶点u不存在B型弱坏邻域, 则假设u至少有6个邻域v1,v2,v3,v4,v5,v6, 分别是3顶点或者是坏顶点.如果v1是3顶点, 则根据图G的极小性, (Guv1)2是(3Δ+4)-退化的, 故假设σ是(Guv1)2的好排序; 否则,v1是坏顶点, 其2邻域w, 根据图G的极小性, (Gv1w)2是(3Δ+4)-退化的, 故假设σ是(Gv1w)2的好排序.在这两种情形下, 均可从σ中删除u,v1,v2,v3,v4,v5,v6及其所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于vi中的坏顶点, 假设vi(i=1,2,3,4,5,6)是坏顶点, 与vi相邻且排在其之前的顶点个数至多为2Δ+5+Δ-3=3Δ+2.对于点u, 在σ′中, 与u相邻且排在其之前的顶点个数至多为Δ-6+6×3=Δ+12.对于vi中剩余的3点, 与之相邻且排在其之前的顶点至多有(2Δ+6)个.对于所有剩余的2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.

2) 若弱好顶点u有1个B型弱坏邻域, 则假设u至少有5个邻域是3顶点或者是坏顶点, 记为v1,v2,v3,v4,v5.如果v1是3顶点, 则根据图G的极小性, (Guv1)2是(3Δ+4)-退化的, 故假设σ是(Guv1)2的好排序; 否则,v1是坏顶点, 其有2邻域w, 根据图G的极小性, (Gv1w)2是(3Δ+4)-退化的, 故假设σ是(Gv1w)2的好排序.在这两种情形下, 均可从σ中删除u、3顶点和坏顶点及其与B型弱坏顶点所有的2邻域, 形成新的排序σ′, 然后在σ′中将删除的点依次加回.对于vi中的坏顶点, 同1).对于点u, 在σ′中, 与u相邻且排在其之前的顶点个数至多为Δ-6+1×4+3×5=Δ+13.对于vi中剩余的3点, 与之相邻且排在其之前的顶点至多有(2Δ+6)个.对于2顶点, 与之相邻且排在其之前的顶点个数至多为2Δ.因此G2是(3Δ+4)-退化的, 矛盾.

3)～6)的证明同2), 故略.

3.2 权转移规则

因为mad(G)≤4, 所以有

(4)

令每个顶点的初始权重为w(v)=d(v)-4, 则易知图G的初始总权重是非正的.通过制定一些权重转移规则, 使得顶点间经过权重转移后, 图G中每个顶点的权重为正, 进而图G的最终总权重为正, 构成矛盾.

对于图G中的点v,d2(v)和d4(v)分别表示点v的2邻域和4邻域的个数.令当ε1,ε2取足够小时, 有由D2和D4的定义, 对于任意的点v, 满足从而可知也成立.

权转移规则7: 每个顶点给权重1+ε1到其每个2邻域, 给权重到其每个3邻域及给权重ε2到其每个4邻域.

下面计算经过权重转移后各顶点的最终权重.

3.2.1 4--点 根据权转移规则7,G中的每个2顶点会从其每个邻域接收1+ε1的权重, 而且不会失去任何权重, 因此其最终权重是w′(v)=2-4+2×(1+ε1)=2ε1>0.

3.2.2 坏顶点 令v是图G的坏顶点.根据权转移规则7,v将权重给相邻的2邻域后, 此时v的剩余权重为-1-d2(v)ε1.此外, 注意到坏顶点不是好顶点和弱好顶点,根据命题13,v不与3顶点和4顶点相邻, 并且v没有坏邻域, 因此v不会再失去任何权重.

综上所述,v的最终权重为正.

3.2.3B型弱坏顶点 令v是图G的B型弱坏顶点.

1) 如果v是B型第一类的, 则根据权转移规则7,v将权重给相邻的2邻域和4邻域后,v的剩余权重是-d2(v)ε1-d4(v)ε2.此外, 根据命题14和命题15,v至多有2个坏邻域, 且每个坏邻域至少有2个优邻域, 由权转移规则10,v至多会失去的权重.如果v有好邻域, 则根据权转移规则11,v至少会接收来自好邻域的权重, 因此v的最终权重是

2) 如果v是B型第二类的, 则根据权转移规则7,v将权重给相邻的2邻域、3邻域和4邻域后, 其剩余权重是根据命题14和命题17,v至多有1个坏邻域, 而且坏邻域至少有2个优邻域, 由权转移规则10,v至多会失去的权重.如果v至少有2个好邻域, 则由权转移规则11,v至少会接收来自其好邻域的权重, 因此v的最终权重是

3.2.4A型弱坏顶点 令v是图G的A型弱坏顶点.

1) 如果v是A型第一类的, 则根据权转移规则7,v将权重给相邻的2邻域和4邻域后, 其剩余权重是1-d2(v)ε1-d4(v)ε2.根据命题14和命题19,v至多有4个坏邻域, 而且坏邻域至少有2个优邻域, 由权转移规则10,v最多会失去的权重, 因此其最终权重是

2) 如果v是A型第二类的, 则当d3(v)=1时, 根据权转移规则7,v将权重给相邻的2邻域、3邻域和4邻域后, 其剩余权重是根据命题14和命题20,v至多有2个坏邻域, 而且坏邻域至少有2个优邻域, 再由权转移规则10,v至多会失去的权重, 故其最终权重是

当d3(v)=2时, 根据权转移规则7,v将权重给相邻的2邻域、3邻域和4邻域后, 其剩余权重是-d2(v)ε1-d4(v)ε2.根据命题14和命题20,v至多有1个坏邻域, 而且坏邻域至少有2个优邻域, 再由权转移规则10,v至多会失去的权重, 故其最终权重是

3.2.5 弱好顶点 令v是图G的弱好顶点.根据权转移规则7,v将权重给相邻的2邻域和4邻域后, 此时v的剩余权重是2-d2(v)ε1-d4(v)ε2.因为v不是好顶点, 所以根据权转移规则7,9,10,12,v会将权重给3邻域、坏邻域及给与之相邻的B型弱坏顶点.若v的邻域中不存在B型弱坏顶点, 则根据命题21中1),v至多有5个邻域是3顶点或者是坏顶点.根据权转移规则7,9,10,v最多会失去的权重, 因此v的最终权重是

若v的邻域中存在1个B型弱坏顶点, 则根据命题21中2),v至多有4个邻域是3顶点或者是坏顶点, 根据权转移规则7,9,10,12,v最多会失去的权重, 因此v的最终权重是

若v的邻域中存在2个B型弱坏顶点, 则根据命题21中3),v至多有3个邻域是3顶点或者是坏顶点, 根据权转移规则7,9,10,12,v最多会失去的权重, 因此v的最终权重是

若v的邻域中存在3个B型弱坏顶点, 则根据命题21中4),v至多有2个邻域是3顶点或者是坏顶点, 根据权转移规则7,9,10,12,v最多会失去的权重, 因此v的最终权重是

若v的邻域中存在4个B型弱坏顶点, 则根据命题21中5), 则v至多有1个邻域是3顶点或者坏顶点, 根据权转移规则7,9,10,12,v最多会失去的权重, 因此v的最终权重是

若v的邻域中存在5个B型弱坏顶点, 则根据命题21中6),v不存在3邻域或者是坏邻域, 根据权转移规则12,v会失去的权重, 因此v的最终权重是

综上所述,v的最终权重为正.

3.2.6 好顶点 令v是图G的好顶点, 并且记d2(v)是v的2邻域个数.如果v不是优顶点, 则对于除去2邻域外的其他(d(v)-d2(v))个邻域, 根据权转移规则7,9,10,11,v会分别给每个邻域至多的权重, 因此其最终权重是

(因为d(v)-d2(v)≥8).

通过上述对顶点间的权重转移, 得到图G中每个顶点的最终权重为正, 因此图G的最终总权重也为正, 与初始总权重非正矛盾.

衷心感谢天津大学应用数学中心彭兴老师的鼓励和指导.