基于序列贝叶斯更新的锂电池剩余寿命预测
2024-03-13刘学娟
赵 斐,郭 明,刘学娟
(1.东北大学 秦皇岛分校,河北 秦皇岛 066004;2.东北大学 工商管理学院,辽宁 沈阳 110819;3.北京科技大学 经济与管理学院,北京 100083)
0 引言
锂电池具有能量密度大、效率高、寿命长等性能,被广泛应用于航空航天、汽车制造、军事通讯等领域[1]。然而,随着锂电池的使用和外部温度等随机因素的影响,其内部不断发生复杂的电化学反应,导致容量和功率不断降低,性能随之退化[2],一旦锂退化量超过阈值,就可能出现绝缘体损坏和短路等问题,若不能及时发现,则有可能引发自燃、爆炸,甚至造成不可估量的损失[3]。因此,准确预测锂电池的健康状态和剩余寿命,对维护电池系统、降低使用成本和事故发生概率至关重要[2]。目前,有关锂电池剩余寿命预测的方法主要有机理模型法、数据驱动法以及将两者融合的方法[4]。其中,基于机理模型方法的预测结果比较准确,然而由于难以精确刻画锂电池退化的电化学反应,预测结果严重依赖于所选取的模型。与之相比,数据驱动方法无需对锂电池退化的内部机理建模,而是基于历史监测信息采用概率统计、随机过程等方法建立锂电池退化模型来预测剩余寿命[5]。
由于容量监测数据更易获取,数据驱动法已受到工业界和学术界的关注。数据驱动法中Gamma过程和逆高斯过程仅适用于对单调退化路径情形建模,而维纳过程更适合描述非单调退化问题,已有不少学者对此展开研究[6]。例如,李军星等[7]通过分析影响硬盘寿命和可靠性的块错误率,采用维纳过程建立了硬盘存储性能的退化模型;唐圣金等[8]利用维纳过程对卫星光纤陀螺进行剩余寿命预测。然而,上述研究均假定维纳过程的漂移系数固定,无法随时间动态更新,即未利用实时监测数据对参数进行动态更新[8]。对此,有学者在假定漂移系数服从正态分布的条件下构建退化模型,并利用初始时刻估计出的漂移系数进行动态更新[9-10]。其中,ELWANY等[9]利用表征轴承退化的振动数据验证了线性维纳过程退化建模的有效性;TANG等[10]将文献[9]中的固定失效阈值进一步扩展为随机失效阈值,构建了线性维纳退化过程模型,并采用贝叶斯方法对失效阈值进行先验估计,继而推导剩余寿命概率密度函数。显然,文献[9-10]并不适用于退化趋势具有高度非线性特征的系统。
为此,许多学者研究了非线性维纳过程,黄亮等[11]基于非线性维纳过程建立发动机的退化模型,利用最大似然方法估计模型参数,同时采用贝叶斯方法更新参数分布,继而预测其剩余寿命;彭才华等[12]提出线性与幂指数结合的非线性退化模型,并采用激光发生器的性能退化数据加以验证;YAN等[13]通过分析旋转机械的退化特征,提出两阶段维纳过程退化模型,采用贝叶斯方法对两阶段退化模型参数进行更新,并以车轮振动踏面数据为例验证了模型的有效性;SI等[14]建立了非线性维纳过程退化模型,采用最大似然方法估计模型参数,并利用陀螺仪和航空材料疲劳裂纹退化数据验证了模型的有效性。以上研究虽然是基于非线性维纳过程建模,但是在模型参数的更新过程中,未利用所有历史退化数据。这是因为维纳过程的独立增量和Markov性质,使贝叶斯更新的漂移系数仅利用了当前观测的退化值,未包含从初始到当前时刻的所有退化值。为解决该问题,LI等[15]采用序列贝叶斯更新方法更新线性维纳过程的退化模型参数,继而以更新的退化模型预测锂电池剩余寿命。
由于锂电池退化不仅与其内部电化学反应相关,还与运行工况有关,例如在寒冷地区,电动汽车的锂电池容量衰减得更快,其退化过程通常呈现为非线性。为此,本文对具有非线性退化的锂电池展开剩余寿命预测研究。首先,采用非线性维纳过程建立锂电池退化模型;然后,基于最大似然估计方法离线估计初始时刻的模型参数;接着,利用实时得到的容量监测数据,采用序列贝叶斯方法动态更新退化模型中的漂移系数,进而预测剩余寿命;最后,选用不同工况(25 ℃,35 ℃,55 ℃)下的锂电池退化数据估计退化模型初始时刻的模型参数,采用45 ℃温度下的退化数据动态更新漂移系数,与幂指数的非线性退化模型和线性退化模型对比,结果表明基于所提非线性退化模型预测出的剩余寿命精度更高。
1 锂电池容量退化建模和参数估计
1.1 基于非线性维纳过程的退化模型
由于锂电池容量会随外部工况变化和内部化学反应而衰减,通常具有非线性特征,为此建立非线性维纳过程的容量退化模型更具适用性[16-17]。令t时刻锂电池容量的退化量
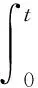
(1)
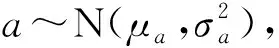
X(t)=x0+a(exp(bt)-1)+σBB(t)。
(2)
1.2 最大似然估计方法离线估计初始时刻的模型参数
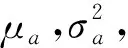
Xj(tj,k)=x0,j+aj(Ψ(tj,k))+σBB(tj,k),
k=1,2,…,δj。
(3)
式中:漂移参数aj为独立同分布;Ψ(tj,k)=exp(btj,k)-1。令T=[T1,T2,…,TJ]T(Tj=Ψ(tj)),向量X=[X1,X2,…,XJ]描述了所有设备的退化数据。根据式(3)和标准维纳过程的独立增量性质,可知Xj服从多维正态分布,均值和协方差分别为:
(4)
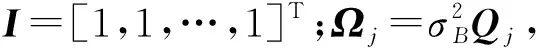
Qj=[min(tj,i,tj,k)]1≤i,k≤δj
(5)
由于设备之间的退化过程具有相互独立性,在监测数据X下构建关于Θ的最大似然估计函数(Θ|X),
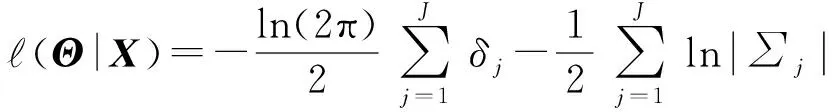
(6)
(7)
(8)
对式(6)求关于μa的一阶偏导,则有
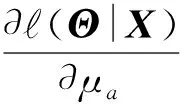
(9)
令式(9)等于0,得到μa的极大似然估计为
(10)
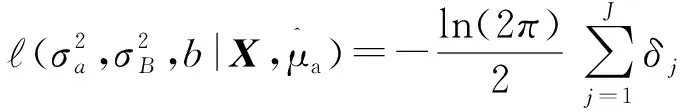
(11)
1.3 序列贝叶斯方法在线更新漂移系数
贝叶斯方法常用于更新非线性维纳过程的漂移系数a,其中a的后验分布P(a|X1:k)不仅与其先验分布P(a)相关,还与实时退化数据的条件似然函数P(X1:k|a)相关。令X1:k={x1,x2,…,xk}表示直至时刻tk设备退化的历史状态监测信息,在tk时刻漂移系数a的后验估计
P(a|X1:k)=
(12)
进一步推导式(12),有
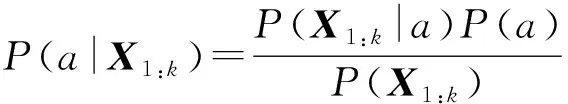
(13)

根据维纳过程性质可知,P(xk|X1:k-1,a)服从正态分布,可表示为
(14)
将式(14)得到的P(xk|X1:k-1,a)和漂移系数a在tk-1时刻的后验估计P(a|X1:k-1)代入式(13),得到a在tk时刻的后验估计P(a|X1:k),

(15)
通过对式(15)进行推导,得到a在tk时刻的参数估计值:
(16)
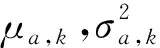
2 锂电池剩余寿命预测模型与流程
2.1 锂电池剩余寿命的预测模型
剩余使用寿命指从当前时刻tk开始,系统首次退化到软失效阈值ω所经历的时间[18]。定义系统在tk时刻的剩余寿命lk为
inf(lk:X(tk+lk)≥ω|X(tk)<ω)。
(17)
在已知漂移系数a的条件下,剩余寿命lk的条件概率密度函数为[15]
fLk|a,X1:k(lk|a,X1:k)≈
(18)
(19)
考虑到漂移系数a的随机性,采用全概率公式计算剩余寿命lk的概率密度函数
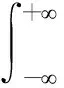
(20)
将式(18)代入式(20),则
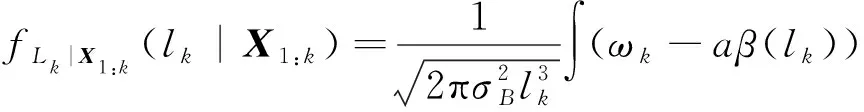
(21)
存在如下引理[14]:若Z~N(μ,σ2),且ω,A,B∈R,C∈R+,则

(22)
(23)
从而得到剩余寿命的期望值
(24)
2.2 锂电池剩余寿命预测流程
结合上述对锂电池容量衰退趋势的非线性退化过程建模,以及模型参数的离线估计和在线估计方法,给出基于序列贝叶斯更新的锂电池剩余寿命预测具体流程,如图1所示。

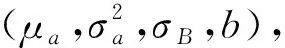
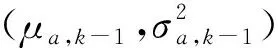
步骤3基于更新的漂移系数估计值,采用式(23)和式(24)分别计算剩余寿命lk的概率密度函数fLk|X1:k(lk|X1:k)和期望剩余寿命E(Lk|X1:k)。
3 实例分析
将所提基于指数函数μ(b,t)=bexp(bt)构建的非线性维纳退化模型X(t)=x0+a(exp(bt)-1)+σBB(t)称为模型1,并将基于幂指数函数μ(b,t)=btb-1的维纳退化模型X(t)=x0+atb+σBB(t)、基于线性函数的维纳退化模型X(t)=x0+at+σBB(t)分别称为模型2、模型3,用于与模型1进行对比分析。在此,引入赤池信息准则AIC比较不同模型的拟合度[19]:
AIC=-2max+2p。
(25)
MSEk=

(26)
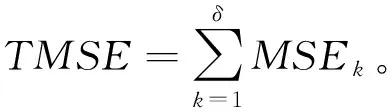
3.1 变工况下锂电池容量退化数据
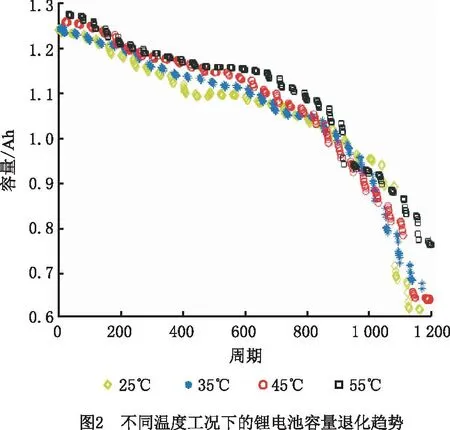
采用变工况下锂电池容量退化数据集验证所提非线性退化模型和参数估计方法的有效性。该锂电池额定容量为1.35 Ah,实验设定初始温度为25 ℃,每经过10个充放电周期温度上升10 ℃,在25 ℃,35 ℃,45 ℃,55 ℃ 4种温度下进行循环实验,容量退化曲线如图2所示,可见锂电池容量退化呈现为典型的非线性特征。
3.2 参数估计与分析
在此将25 ℃,35 ℃,55 ℃ 3组变工况下的锂电池退化数据作为训练数据集,将45 ℃工况下的锂电池退化数据作为测试数据集,设定失效阈值ω=0.64。利用图1中的参数估计方法,基于训练数据集估计出3种退化模型初始时刻的模型参数,得到对应的最大对数似然函数值Log-LF和AIC值,如表1所示。其中,模型1的Log-LF=166.311 0,AIC=-326.622,与模型2和模型3的结果相比,模型1的Log-LF值最大、AIC值最小。根据Log-LF值越大、AIC值越小,所估计出的模型拟合效果越好这一判断准则,由表1可知,所提非线性退化模型1更适用于变工况下的锂电池容量退化过程建模。
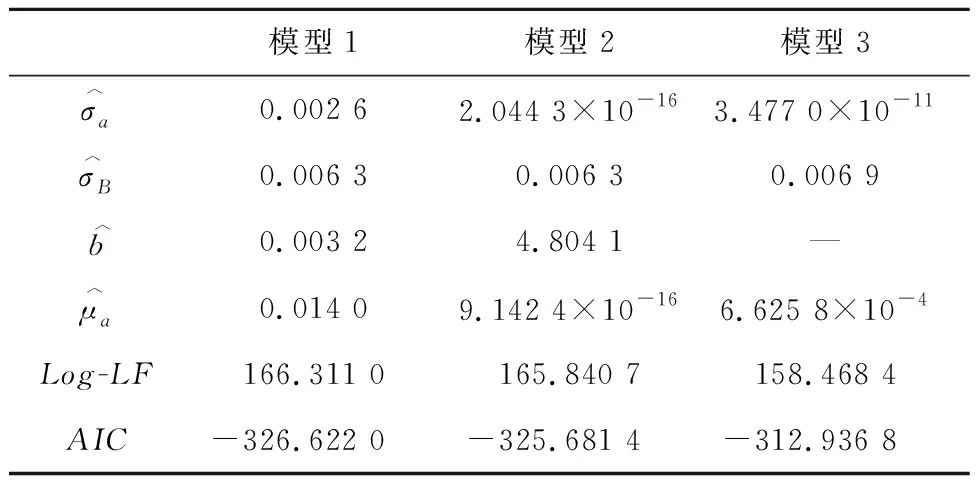
表1 锂电池容量退化模型的参数估计结果
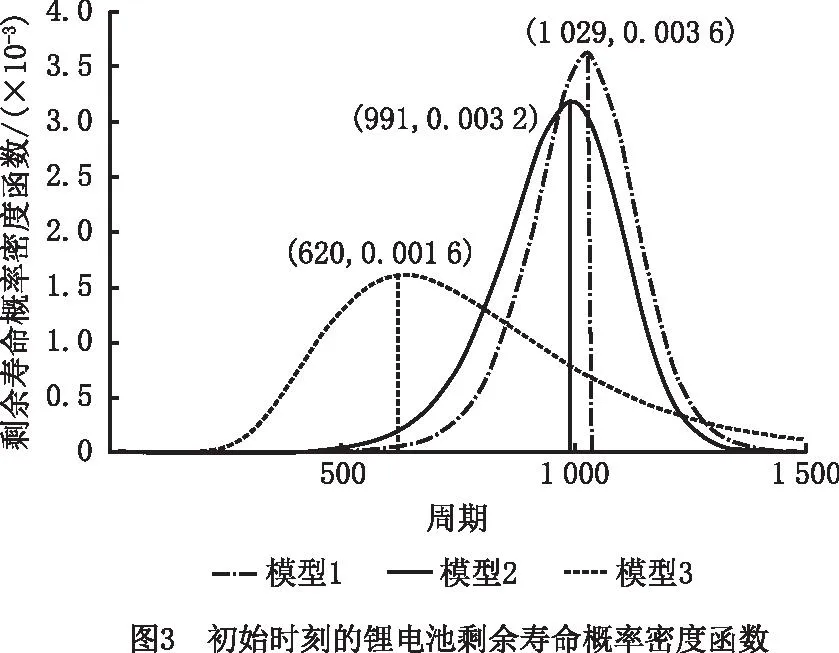
基于表1估计得到初始时刻模型参数,推导不同退化模型下的剩余寿命概率密度函数,如图3所示。可见,初始时刻模型1得到的峰值为0.003 6,高于模型2和模型3的峰值0.003 2,0.001 6;模型1峰值对应的周期为1 029,模型2和模型3峰值对应的周期分别为991和620,显然模型1更接近真实的周期值1 070。因此,由模型1预测出的剩余寿命误差更小,精度更高。
3.3 剩余寿命预测结果与对比
进一步以45 ℃工况下锂电池容量退化数据作为测试集动态更新模型参数,对比3种退化模型下各监测时刻的锂电池剩余寿命概率密度函数、平均值和实际剩余寿命值,如图4所示。由图4a~图4c可见,在初始监测阶段,锂电池的剩余寿命概率密度函数曲线均较平缓,这是因为初始时刻获取的容量退化状态数据较少,导致估计参数时漂移系数a估计值的不确定性增大,进而使预测误差偏大;然而,随着监测时间的增长,剩余寿命概率密度函数曲线呈现逐渐增高的趋势,说明随着监测状态数据的增加,对模型中漂移系数a估计的不确定性变小,从而使预测误差逐渐减小。由最后一个周期(1 070)的概率密度函数曲线可见,模型1和模型2的概率密度函数曲线峰值依次约为0.017 1和0.016 5,明显高于模型3的峰值0.006 6,这是因为模型1中的漂移参数是根据截止到当前时刻的所有退化监测数据实时估计的,克服了仅利用当前退化数据进行参数估计的不足。
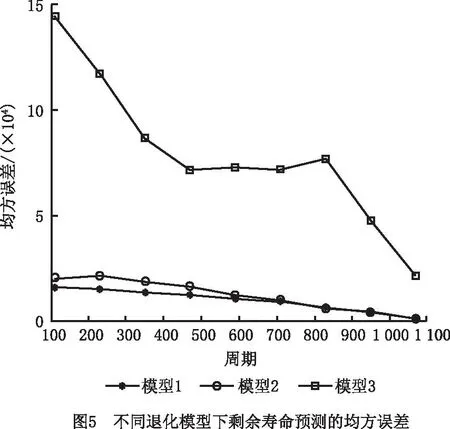
图5所示为3个模型不同周期上对应监测时刻的均方误差值。可见,随着监测周期的增加,必然会获取更多的监测数据,使得任一模型的预测误差均逐渐减小,但模型1的均方误差小于模型2和模型3,尤其比线性退化模型3要低。计算得出3个模型的TMSE值分别为9.034 1×104,11.188×104,71.130×104,最后一个监测周期的均方差分别为1 281.454 9,1 397.898 4,21 431.437 2,进一步表明模型1的预测精度最高。
4 结束语
考虑到锂电池在实际运行时因受温度、材料化学反应等因素影响,容量退化通常呈现为非线性特征,本文提出基于指数函数的非线性维纳过程模型描述锂电池容量退化。传统贝叶斯更新方法在估计退化模型参数时仅利用当前时刻的监测数据,忽略了锂电池历史退化趋势的影响,为此采用离线估计和在线更新相结合的方法估计参数,推导剩余寿命概率密度函数并进行预测。其中,基于收集到的锂电池历史退化数据,利用最大似然估计方法离线预估退化模型的参数,进而采用序列贝叶斯更新方法在线更新非线性退化模型中漂移系数的参数。以25 ℃,35 ℃,55 ℃ 3种不同温度下的锂电池退化数据集估计初始时刻的模型参数,在此基础上以45 ℃的锂电池容量退化数据对漂移系数进行在线更新并预测剩余寿命。通过与其他退化模型对比表明,所提基于指数函数的非线性维纳过程退化模型具有较高的最大对数似然函数值和较小的AIC值,拟合效果更好,而且预测的剩余寿命精度更高。
本文研究将温度视为影响锂电池容量退化的工况,而针对运行工况更加复杂的系统,系统退化可能受温度、负载等多因素影响,而且不同因素对退化的影响机制也不同,这将在后续研究中进一步探讨。
