数据挖掘算法在作业车间调度问题中的应用
2024-03-13王艳红赵也践刘文鑫
王艳红,赵也践,刘文鑫
(沈阳工业大学 人工智能学院,辽宁 沈阳 110870)
0 引言
车间调度在生产制造中扮演着重要的角色,一直是控制科学和制造领域的研究热点。作业车间调度问题(Job Shop Scheduling Problem,JSSP)是车间调度领域中的经典案例,具有NP-Hard特性[1],即难以通过遍历所有可行解来获得最优解。传统的JSSP优化方法分为最优化方法和近似优化方法两大类。最优化方法能够获得JSSP的最优解,这类方法包括数学规划法(mathematical programming)、分支定界法(branch and bound)和枚举法(enumerative methods)等,然而这些方法只能求解小规模JSSP案例,随着算例规模的不断增大,可行解空间的规模会以指数形式增大,而遗传算法(Genetic Algorithm,GA)[2]、粒子群优化(Particle Swarm Optimization,PSO)算法[3]等经典的近似优化方法虽然可以求取大规模JSSP的近似最优解,但是存在耗费时间更多和需要反复调参等缺陷。
随着信息技术的发展与应用,车间在生产中积累了越来越多的离线或在线生产数据,这些数据中隐藏着大量可以反映和指导求解JSSP的调度信息,如果能够高效利用这些生产数据,并使用某些技术提取出可靠的调度知识来提高调度算法的优化能力,则可提高作业车间的加工效率。传统的数据处理与分析技术在处理当今海量数据时具有局限性。数据挖掘(Data Mining,DM)技术打破了这些瓶颈,使用DM技术从离线数据中获取隐含在加工过程中的有效调度知识来分析与优化调度算法,进而指导作业车间的调度过程,成为一种求解JSSP的新思路。同时,这些调度知识能够保留并增强原有调度算法的优化能力,生成更加接近最优解的较优调度策略,在JSSP调度过程中具有重要的意义。
从历史生产数据中挖掘的调度知识中,调度规则(Dispatching Rules,DRs)是其一种重要的表现形式,也是在JSSP中常用的近似优化方法,其用于解决在同一时刻同一台机器上进行加工的作业的冲突问题,并被证明是求解JSSP常用且有效方法之一[4]。DRs从长期积累的调度问题的专家知识抽象而来,但传统的DRs性能较差,且不存在任何一个DR在不同生产场景和性能指标下优于其他规则的调度性能[5]。因此,一种基于数据挖掘算法(Data Mining Algorithm,DMA)的调度方法可以解决该问题,该方法通过从作业车间自身隐含的离线生产数据中提取若干有效的DRs嵌入GA等优化算法来求解JSSP。
HUYET等[6]开发了一种基于DM的方法来优化生产系统的设计和配置; HUYET[7]在车间调度问题上使用了相同的方法;LI等[8]介绍了一种使用数据驱动方法生成DRs的新方法,展示了通过将学习算法直接应用于生产数据并使用DMA发现以前未知DRs的详细过程;BAYKASOGLU等[9]提出一种基于遗传编程的DM方法来选择DRs,以根据当前生产车间参数选择最合适的DRs;BALASUNDARAM等[10]采用DMA中的决策树算法从调度数据提取易于理解的特定调度规则,用来求解具有两台加工机器的车间调度问题;焦磊等[11]针对生产数据的特点,提出一种基于动态聚类的DM方法来挖掘DRs;林谷雨等[12]采用DMA中的决策树学习算法发现离散车间中的调度知识;SHAHZAD等[13]为了解决元启发式算法在求解车间调度中实时计算量较大的问题,采用决策树离线提取车间中的if-then DRs,并将其应用到在线车间调度问题中;王成龙等[14]针对JSSP提出一种结合分支定界法和DMA中决策树的DRs挖掘方法,该方法能够提取隐藏在优化调度方案中的调度知识,在算例中得到了更小的完工时间;JUN等[15]为了求解动态单机调度问题,提出一种将调度转换为包含底层调度决策的训练数据并生成基于决策树的DRs的方法,实验表明,在最小化平均总加权延迟这一性能指标下,该方法优于其他调度规则。
从以上文献可见,目前在JSSP中使用DMA挖掘DRs并优化调度算法的研究还比较少。本文以JSSP为研究对象,以最小化最大完工时间为性能指标,提出一种基于DMA的JSSP调度框架,来挖掘历史生产数据中的调度知识(即DRs),进一步建立了该数据框架下面向改进GA的JSSP调度优化算法。所提取的DRs能够进一步优化调度算法,改善调度算法性能。最后通过计算机仿真实验验证了所提调度算法的有效性。
1 JSSP的问题描述与数学模型
在JSSP中,设有n个待加工工件J={J1,J2,…,Ji,…,Jn}需要在m台机器M={M1,M2,…,Mg,…,Mm}上加工。每个工件Ji要经过ni道不同的加工顺序,已知各工序的加工时间和Ji在各机器上的加工次序约束。JSSP的任务目标是,明确为各个工件的每一道工序选择合适的加工机器,确定其开始加工时间以及每一台机器上工件的加工顺序,从而使调度结果满足预期的性能指标。
为了简化当前的JSSP,本文设定如下约束:①所有的机器准备时间为0,即所有工件到达机器后都能立即开始加工;②按照加工工艺规定,每道工序必须在其之前工序加工完成后方可开始加工;③各个工件必须按照工艺路线以指定的次序在机器上加工,而且假定不同工件之间具有相同的优先权;④每一时刻每台机器只能加工一个工件,某一时刻每个工件只能被一台机器加工;⑤工序一旦开始加工不可中断;⑥前一个操作未完成,后面的操作需要等待;⑦各工件的准备时间和完成时间一起计入加工时间。
在问题描述中涉及的参数如表1所示。

表1 JSSP的问题描述参数
本文采用最小化最大完工时间为性能指标,按照JSSP的特性设定若干约束条件,其数学表达式如下:
minJ=minCiMk。
(1)
ciMk≥tiMk;
(2)
ciMk-tiMk+β(1-aiMhMk)≥ciMh;
(3)
clMk-ciMk+β(1-bilMk)≥tlMk。
(4)
其中:式(1)表示性能指标为最小化最大完工时间;式(2)表示Ji在Mk上的完工时间CiMk不能小于其加工时间tiMk;式(3)表示工件Ji的前后两道相邻工序在机器Mh和Mk上加工的顺序约束,且当Mh先于Mk加工Ji时,aiMhMk=1,否则aiMhMk=0;式(4)表示机器Mk完成一个加工任务后才能开始另一个加工任务,且当Ji先于Jl在Mk上加工时,bilMk=1,否则bilMk=0。β表示一个具有很小正值常数的调节因子。
2 DMA提取DRs的过程分析
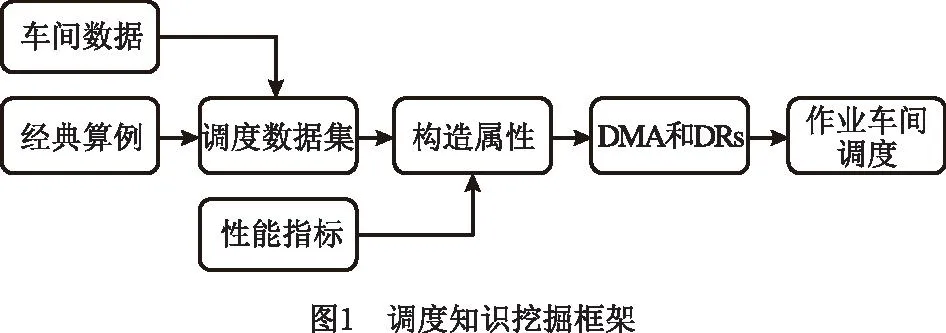
2.1 调度知识挖掘框架
本文主要研究的是,针对JSSP的数学模型、作业车间的相关属性以及不同类别的算例(每个算例的工件数量、机器数量和每个工件的工序数量不同)挖掘以DRs的形式存在的特定调度知识。挖掘到的DRs并非一成不变,而是随算例或车间实例的增加不断丰富,使逐渐形成的DRs库适用于更多的JSSP案例。因此本文提出一种使用历史调度数据框架挖掘DRs的方法。图1所示为调度知识挖掘框架结构图,其中DMA能够揭示调度数据中隐藏的、用于进一步强化调度决策的调度知识。
2.2 决策树算法
决策树是构建决策模型时常用的方法,其由节点和叶子组成,有关参数值的决策在节点进行。决策树通过逐层决策,最终使树的底部叶子形成某些特定的类别。
决策树包括ID3算法、C4.5算法和分类回归树(Classification And Regression Tree,CART)算法等。在以往使用DMA求解JSSP的研究中,ID3算法和C4.5算法虽然是主流求解工具,但是存在如下弊端:
(1)ID3算法利用信息增益作为决策树选择属性的依据,其通用性强,适合大多数分类问题,且建树思路简单,成为DM技术领域中颇有影响的算法之一。该算法的主要缺点是不能处理连续型样本属性和存在缺失值的样本集,因此出现了C4.5算法。
(2)C4.5算法采用信息增益率选择属性作为决策树的节点,增加了剪枝和处理连续型数据等功能,不足之处是只能求解分类问题,不能求解回归问题。另外,C4.5算法生成的可视化决策树属于多叉树,许多情况下计算机对多叉树的求解效率相对较低,因此设计了基于二叉树的CART算法来解决这些问题。
CART算法所生成的决策树的任意节点有且仅有两个分枝结果,该决策树被称为CART二叉分类树(以下简称CART树),其目的是减小树的深度,加快计算机的处理速度,因此被广泛应用于求解各类分类问题和回归问题。表2对这3种常用的决策树从算法结构、剪枝效果及扩展性进行了比较。

表2 常用决策树对比
JSSP中包括很多工件或机器的相关属性,每个工件的各种属性都具有一定相关性,例如工件的加工时间属性有长和短两种关系,交货期属性也有提交的早或晚等关系,符合CART树的特点,因此本文选取CART树对DRs进行挖掘。
CART树的根节点是所有样本中基尼指数最小的属性,在根节点以下所有子树包含的中间节点均在样本数据子集中利用基尼不纯度最小化原理构建形成,样本训练集的类别值构成了CART树的叶子节点。CART树的结构如图2所示。

2.3 基于CART树的DRs挖掘过程
2.3.1 CART树的执行过程
CART树通过计算基尼不纯度系数来确定属性划分点,数据集所含的信息量采用基尼不纯度系数来衡量[16]。
假设有K个类别,样本点属于第k个类的概率为Pk,则概率分布的基尼不纯度系数的数学公式为
(5)
根据基尼系数定义得到样本数据集U的基尼指数
(6)
式中Ik为U中属于第k类的样本子集。
如果U根据特征A在某一取值a上进行分割,得到U1和U2两部分,则在特征A下集合U的基尼系数为
Gini(U,A)=
(7)
式中:基尼系数Gini(U)表示从U中随机抽取两个样本,其类别标记不同的概率,其值越小,U的纯度越高,分支越好;基尼系数Gini(U,A)表示A=a分割后集合U的不纯度。
将CART树挖掘DRs的详细步骤进行如下描述,具体的算法流程如图3所示:
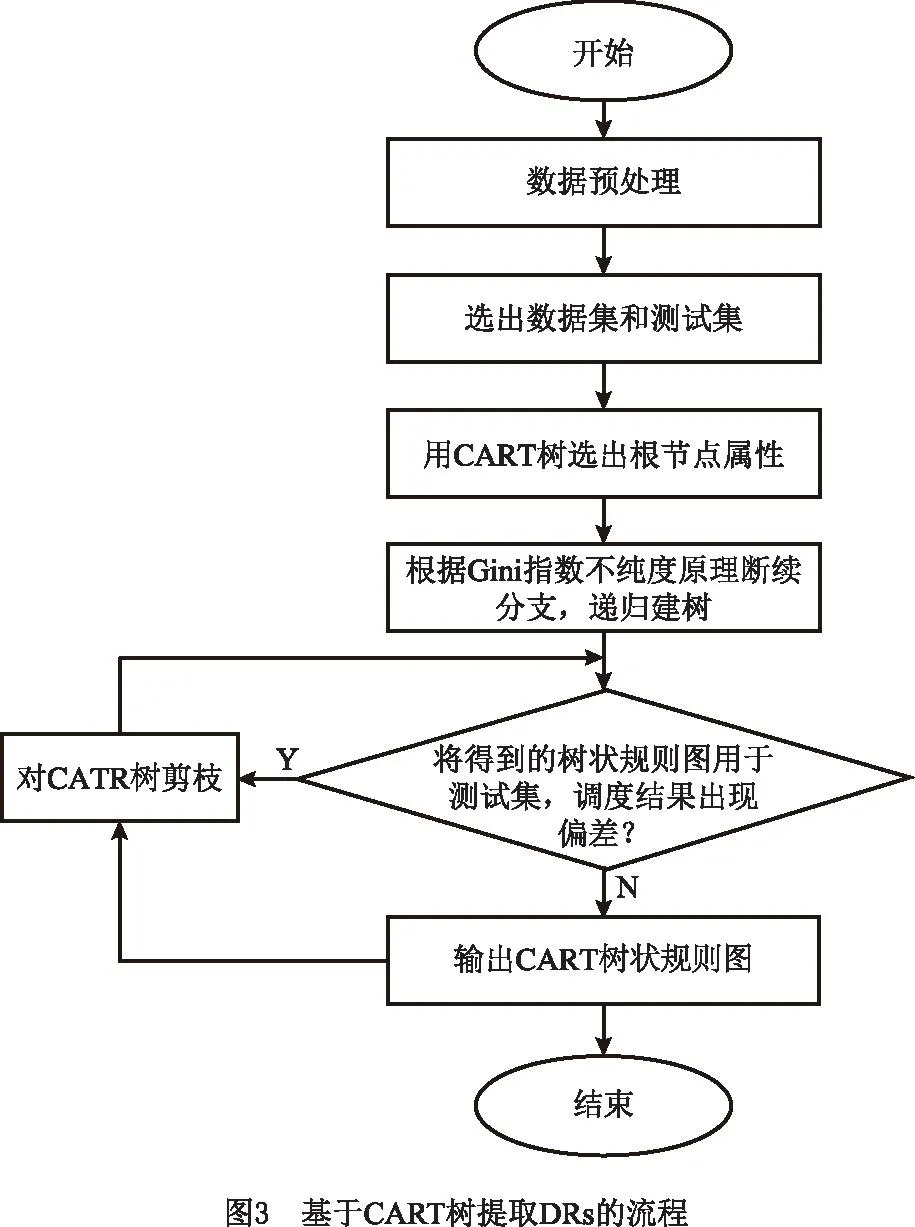
(1)对调度数据集进行数据预处理。
(2)从调度样本集中选出训练集和测试集。
(3)在训练集中运用CART树,选择基尼指数最小的属性作为树的根节点。
(4)在根节点的基础上,按照基尼指数最小化原理,将其他属性作为根节点之下的叶子节点并继续分类,依次递归成树图。若训练集中仅剩一个分类类别,则不再分裂。
(5)将(4)得到的DRs运用到测试集中,观察调度结果是否存在偏差,是则对CART树进行剪枝,重复(5),直到每个测试子集调度结果与测试集基本相同。
CART树表示DRs的流程包括数据选择、数据预处理、建树、剪枝。
2.3.2 数据选择
数据选择过程一般选择作业车间中的实际生产案例作为对挖掘有利的调度样本集。本节的调度样本集选自文献[17]中“10个工件在1台机器上加工”的单机调度案例(单机调度问题中的10个工件视为10道工序),如表3所示。

表3 单机调度算例数据
2.3.3 数据预处理
采用数据预处理技术挖掘有效调度知识的前提是对历史调度数据进行转换,调度问题数据预处理的关键是确定调度样本集的属性标签和属性类别。
为了更好地说明基于数据的DRs的产生过程,本节通过“权重”和“交货期”这两个属性为基础选择相关的工序信息作为调度样本集的属性,具体如下:
(1)提交时间(Release Time,RT) 表示某道工序(若为单机调度,则表示为某个工件,余同)可以加工的最早时间。
(2)交货期(Due Time,DT) 表示某道工序完成加工的最后期限。
(3)加工时间(Processing Time,PT) 表示某道工序在机器上加工的时间。
(4)权重(Weight,W) 表示某道工序相对于其他工序的重要性。
首先,对以上4个属性的初始值进行离散化。对于机器M可同时加工的两个工件,分别比较4个属性值,将所得结果作为样本集的属性。依次比较10个任务的属性,预处理后得到以下4个新属性:
(1)Job1_release_earlier 同一机器上的两道工序谁的提交时间更早。
(2)Job1_due_earlier 同一机器上的两道工序谁的交货期更早。
(3)Job1_weight_higher 同一机器上的两道工序谁的权重更大。
(4)Job1_processing_lower 同一机器上的两道工序谁的加工时间更短。
进一步比较上述4项属性的样本数据:
(1)对于Job1_release_earlier,Job1_due_earlier,Job1_processing_lower 3个属性,任意两个工件对比后(每次对比的第1个工件记为Job1,第2个记为Job2),第1个工件属性数值较小的记为1,数值较大的记为0,Job1_weight_higher则相反。若出现属性数据相等的情况(如表4的Weight属性),则全部记为1。
(2)对于加工序列属性,将优先加工的工序用Job1_first表示(该类别简记为1),后加工的工序用others_first表示(该类别简记为0)。
以表3中的一部分工件数据为例,用表4说明Job1_release_earlier的由来,其他3个属性标签的生成同理。
表4中,No.1表示表3单机调度算例中的”Job索引”为1。根据表3的算例数据,共有10个工件,每2个工件需要一一对比4个属性数据,得到45组数据,结合上述数据预处理以及表3中的“加工序列”这一列,得到该算例数据预处理表,如表5所示。
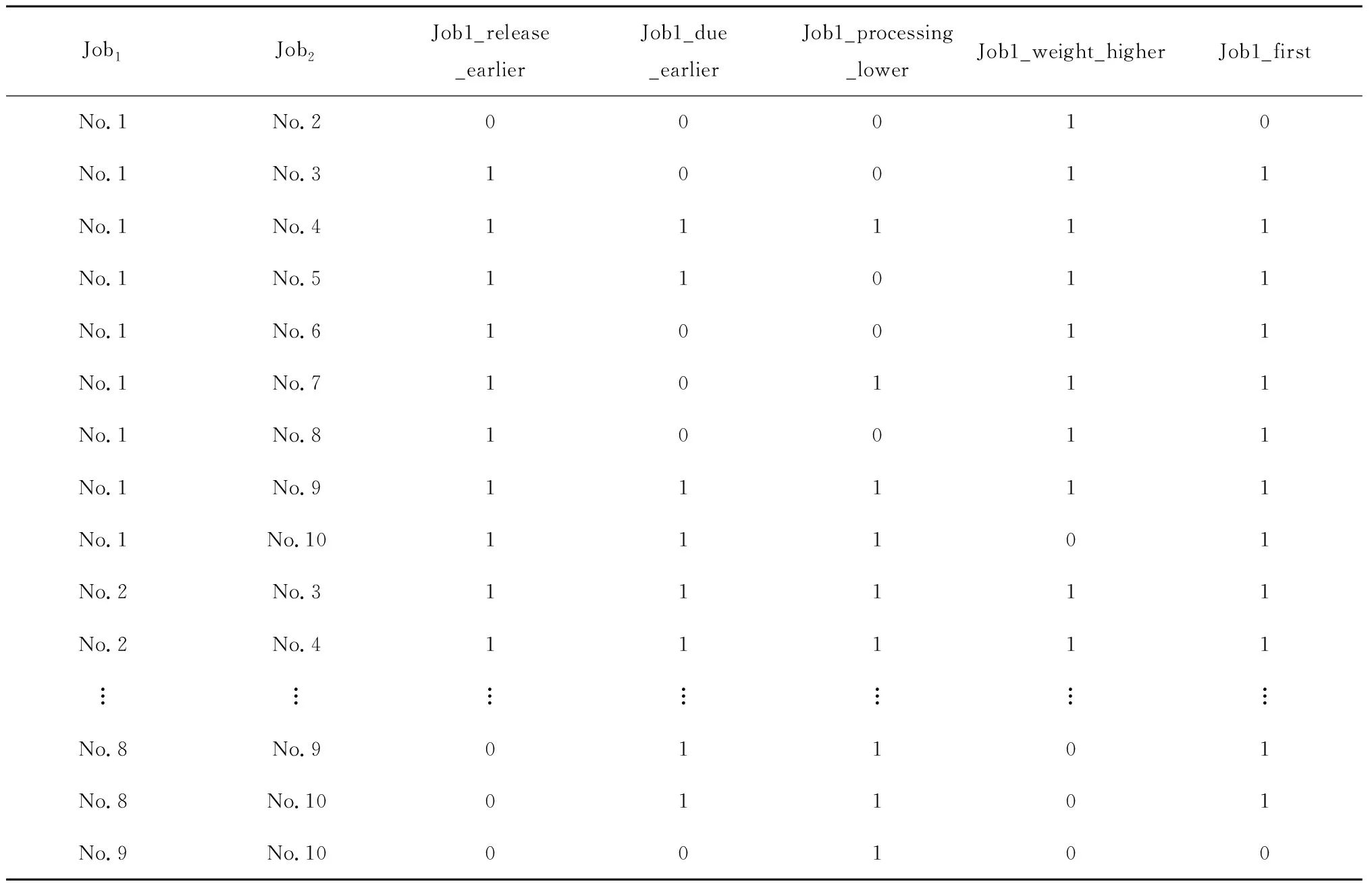
表5 数据预处理
表5中,No.1表示表3中的Job索引为1;该表为45组对比数据,限于篇幅,省略其余组数据;Job1_first为0的情况实际上对应others_first类别。
2.3.4 建树
CART树根据“各属性的基尼指数最小”这一标准选择树的决策节点,并以此建树。在调度样本集中,分别计算各调度属性特征的基尼指数并进行比较,选择各层属性节点。
表5中有Job1_release_earlier,Job1_due_earlier,Job1_processing_lower,Job1_weight_higher 4个属性,以及Job1_first的1和0两个类别。有如下假设:
(1)假设4个属性依次为特征RT,DT,PT,W。
(2)假设RT1,DT1,PT1,W1分别为特征RT,DT,PT,W为1的情况,RT2,DT2,PT2,W2分别为特征RT,DT,PT,W为0的情况;同理,F1为类别Job1_first为1的情况,F2为类别Job1_first为0(others_first为1)的情况。
(3)分别计算各特征的基尼指数,找到最优特征和最优切分点。
由表3算例样本集及表5的调度结果数据预处理可知,在表5中的45个样本中,有25个类别Job1_first为1的正例和20个类别Job1_first为0的负例,即F1为25,F2为20;在特征RT处取值为1的例子有32个,即RT1为32,取值为0的例子有13个,即RT2为13。得知特征RT的真正例有20个,假真例有12个,真负例有5个,假负例有8个。同理得到其他特征的这些信息,各特征详情如表6所示。

表6 各个特征信息
根据表6,结合式(6)求出RT1所属集合U1和RT2所属集合U2的基尼指数分别为:
(8)
(9)
再由式(7)求得特征RT的基尼指数
(10)
同理可得:
Gini(U,A=DT)=0.485;
(11)
Gini(U,A=PT)=0.48;
(12)
Gini(U,A=W)=0.432。
(13)
由此可知,Gini(U,A=W)=0.432远小于Gini(U,A=RT)=0.47和Gini(U,A=DT)=0.485,因此取Job1_weight_higher为CART树的根节点。继续按照这样的分裂规则选出其他叶子节点,直到因基尼系数为0,或者叶子节点样本数量不足,无法再形成分支时结束分裂。以此类推,CART树完成建树过程。
2.3.5 剪枝
CART树对训练集进行测试时很容易产生过拟合,导致泛化能力变差。在对JSSP算例进行数据挖掘后,会挖掘出一个包含若干DRs的初始DRs库,因为有些DRs或者冗余或者已存在,所以这些DRs并不会改善调度问题的求解精度,反而会浪费系统资源。因此,很有必要对CART树进行剪枝,这一过程与线性回归的正则化表达相似。CART树的剪枝是“测试集对现有生成树加以剪枝并挑选出最优树集”的过程,一般将“损失函数最小化”作为决策树剪枝的原则。决策树剪枝的方法有预剪枝和后剪枝,CART树采用后剪枝,其过程是先从训练集生成一棵完整的决策树,再自底向上检验非叶子节点。若将该节点对应的子树替换为该节点能提高树的性能,则用该节点替换该节点对应的子树。
决策树剪枝中不仅看特征的基尼系数是否为0或者小于一定的阈值,还需要关注决策树的最大深度max_depth、内部节点再划分所需的最小样本数min_samples_split、叶子节点最少样本数min_samples_leaf、最大叶子节点数max_leaf_nodes等参数。
2.4 实验仿真与结果分析
为了验证以上关于挖掘DRs理论的可行性,现以表4中的单机调度算例为例,用CART树挖掘隐藏的DRs。仿真实验在加速频率为2.20 GHz的Inteli5-4500U处理器、运行内存为4 GB的Windows 7 PC平台进行,采用Python程序编写,编译环境为Python Jupyter,编译器版本为Python 3.7.3。仿真程序是通过网格搜索法对CART树进行多次剪枝,直到仿真出的树状规则满足调度样本测试集的加工顺序,程序中DecisionTreeClassifier模块的各参数为max_depth=3,min_samples_split=9,min_samples_leaf=8,max_leaf_nodes=5。经过39.973 s运行,剪枝完的CART树状规则图如图4所示,从而得到最终的决策树。
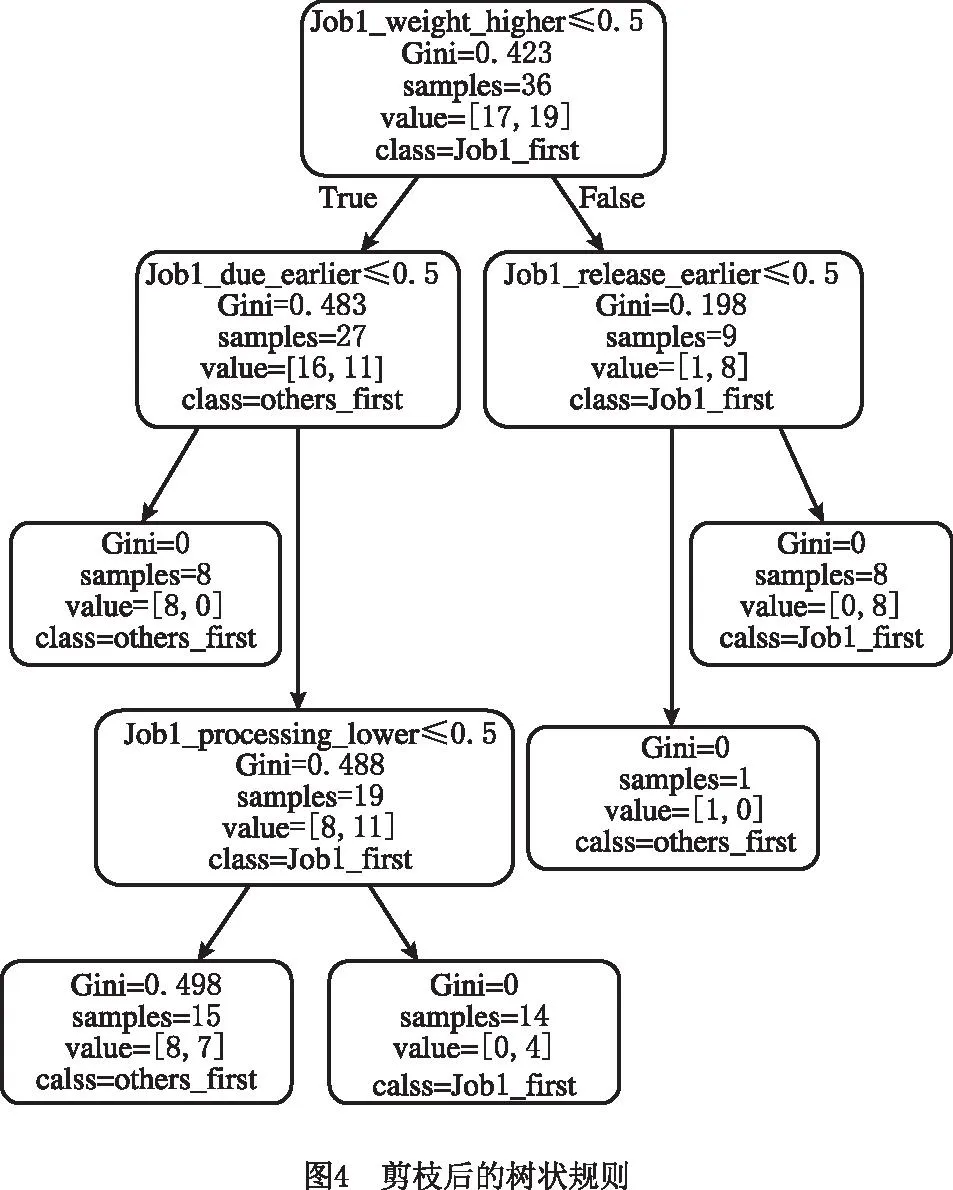
在表4中,由2.3.3节可知,Job1_weight_higher和Job1_due_earlier两个属性特征尤为重要。由图4同样可知,CART树状规则图的根节点属性为Job1_weight_higher,与2.3.4节求得的结果相同,而且根节点的基尼不纯度指数也与公式演算出的相同。从图4可知,CART树第1层节点的属性为Job1_due_earlier和Job1_release_earlier,最后才是Job1_processing_lower,进一步证实了CART树在求解基于DMA的JSSP的有效性和准确性。
针对图4的CART树,其自上而下的直线箭头方向形成的路径便是需要描述的DRs。因为CART树是二叉分类树,且每个属性值均小于等于0.5,所以真实规则的True和False正好相反,得到如下DRs:
(1)If Job1_weight_higher=True and Job1_release_earlier=True,Then Job1_first=True。
(2)If Job1_weight_higher=True and Job1_release_earlier=False,Then Job1_first=False(others_first=True)。
(3)If Job1_weight_higher=False and Job1_due_earlier=False,Then Job1_first=False(others_first=True)。
(4)If Job1_weight_higher=False and Job1_due_earlier=True and Job1_processing_lower=True,Then Job1_first=True。
(5)If Job1_weight_higher=False and Job1_due_earlier=True and Job1_processing_lower=False,Then Job1_first=False(others_first=True)。
以上5条DRs简单描述为,同一时刻两道工序竞争同一台设备时:
(1)若第1道工序的权重更大,且第1道工序在第2道工序之前提交发布,则优先加工第1道工序。
(2)若第1道工序的权重更大,且第1道工序在第2道工序之后提交发布,则优先加工第2道工序。
(3)若第1道工序的权重更小,且第1道工序在第2道工序之后完工交货,则优先加工第2道工序。
(4)若第1道工序的权重更小,且第1道工序在第2道工序之前完工交货,第1道工序的加工时间更短,则优先加工第1道工序。
(5)若第1道工序的权重更小,且第1道工序在第2道工序之前完工交货,第1道工序的加工时间更长,则优先加工第2道工序。
3 基于DMA和DRs的GA调度算法
为了验证CART树挖掘出的DRs的有效性,本文提出一种基于DMA的改进GA调度算法。同时,来自车间的数据也可以用作训练样本或测试样本,以创建新的DRs或修改现有的DRs。
3.1 基于GA的JSSP调度算法
GA是在1975年由Holland等专家基于生物有机体的遗传过程提出的一种优化方法,可用于解决NP-Hard优化问题。以往研究曾用“强方法”和“弱方法”来描述各种优化算法与待求解问题的相关性。基本的GA属于一种通用算法,因此被划为“弱方法”,在求解某些实际问题时,需要将GA转化为“强方法“来提高求解效率,同时获得更好的求解质量。因此在JSSP中,可以在GA中嵌入DRs来对基本GA进行改进,使其成为专门求解JSSP的改进GA调度算法,该算法在解决组合优化生产调度问题等NP-Hard问题的效果十分显著。
在基于数据的调度框架基础上,本文将CART树直接应用于历史生产数据,通过数据挖掘发现新的DRs,再将由系统积累数据获取的DRs同GA结合,进行DRs优化,提出一种基于DMA和DRs的GA调度算法(Genetic Algorithm based on Data-mining and Dispatching Rules,GA-DDR)。该算法是在基本GA的基础上嵌入通过DMA获得的DRs来进行全局优化,有助于加快算法的求解速度和收敛速度。GA-DDR调度算法的步骤为:
(1)采用CART树得到未知的新型DRs。
(2)将所获得的DRs嵌入GA进行调度优化,并指导后续车间类似的调度问题。
这样使GA的子代种群逐渐优化,加快了得到最优解的速度,并减少了GA的总迭代次数。
GA-DDR调度算法的具体流程如图5所示。
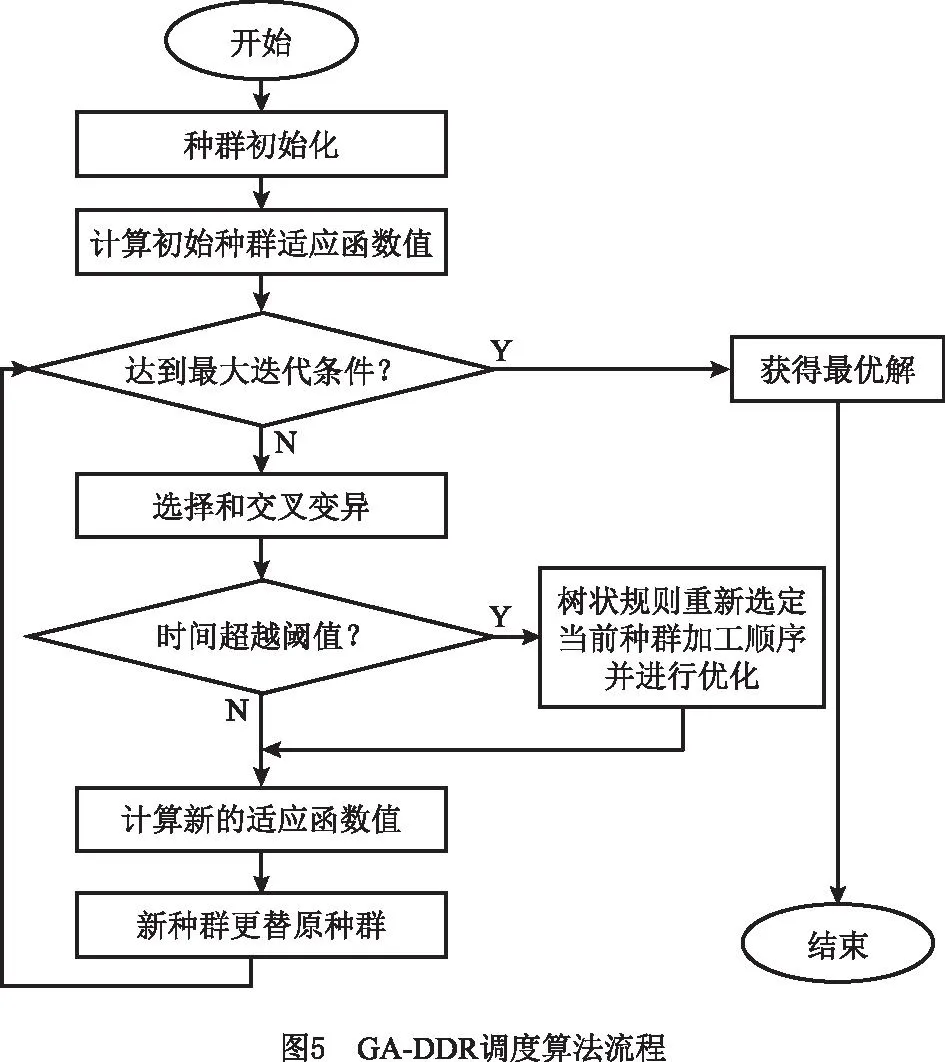
3.2 GA-DDR调度算法流程
GA-DDR调度算法由染色体编码、种群初始化、适应度函数、遗传操作(选择、交叉和变异)等步骤组成。
3.2.1 染色体编码
本文采用基于工序的基因编码表示个体,一组编码代表一种可行的加工方案。例如,一组工序码为“1 2 4 3 4 3 1 2 2 4 3 1 3 2 4 1”,每个数字表示待加工的工件序号,同一数字第几次出现表示对应工件的第几道工序,例如第1个“4”表示4号工件的第1道工序,即O41。
3.2.2 种群初始化
首先定义如下参数:
Nij为第i个工件第j道工序的加工机器编号;
OPmax为所有工件的最大工序数。
由此可知,N是一个n×OPmax的矩阵,即Nn×OPmax为机器顺序阵。
初始群体:
(1)先计算“待加工工件“在CART树中的根节点属性值,再从其最大或最小集合中选取一个工件i(比较根节点的属性值后,比较下一节点的属性值,直至比较完毕),得到Ni1。
(2)Nig=Ni(g+1),r=OPmax-1,NiOPmax=0。
(3)如果N的所有元素均为0,则结束,否则转(1)。
至此,DRs与GA完成结合,并得到基于DRs的初始种群群体。该初始种群基于DRs定义并生成,所有新个体的生成均基于该方法完成。
3.2.3 适应度函数

本文的性能指标为“最小化最大完工时间”,相当于求问题f(x)的最小值。为了方便算法选择更接近目标函数值的下一代个体,可以使目标函数值与一个随机数的和的倒数作为个体的适应度值,这种适应度函数会明显增强不同个体之间的差异,进而加快收敛速度。设i为个体x对应的解,Cmin为个体x对应的完工时间最小值,则个体x对应的适应度函数
(14)
3.2.4 遗传操作
(1)选择操作
选择时以适应值为选择原则,通过适应度函数进行评估。具体过程为在种群繁殖阶段,从种群中随机选择个体进行重组产生后代,这些后代构成下一代;然后从群体中随机选择两个父代,通过交叉变异产生更健康的个体继续繁殖。
本文采用轮盘赌法选择个体,计算公式为
(15)
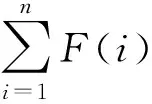
(2)交叉操作
本文采用扩展后的多点交叉法进行交叉操作,具体过程如下:
1)选取两组染色体序列P1和P2。
2)随机产生一个随机数s,比较s与pc,如果pc>s,则进行正常的多点交叉操作,将父代P1和P2的基因段互换,记对换基因个数点为g;如果pc
3)令g=g+1,重复步骤2),直到g等于多点交叉总对换基因的个数,生成新的子代C1和C2。
(3)变异操作
变异是通过替换个体染色体上的某些基因形成新个体来保证种群多样性。本文采用“动态改变变异概率”(根据适应度值决定变异概率)随机交换选中个体上两个位置的基因,然后判断相对应的工件工序是否满足工序条件,满足则进行变异操作,否则重新调整染色体上的基因位置。
4 仿真研究与结果分析
本文的实验仿真分为3部分:
(1)为了初步展现GA-DDR调度算法在求解JSSP上的逻辑性,选取“15个工件在5台机器上加工”的LA06算例进行研究,将所得结果与不包含DMA和DRs的基本GA算法求解JSSP的结果进行比较,分析两种算法在收敛性方面的差异并得出初步结论,为其他实验提供理论依据。
(2)为了进一步验证GA-DDR调度算法的有效性,先对LA01算例的加工数据进行数据预处理、选择属性标签、数据挖掘等操作,获得新的树状DRs,进而形成GA-DDR调度算法,用该算法求解LA11,LA17,LA24,LA26,LA33,为后续其他大量的测试算例做准备。
(3)选取40个LA经典JSSP算例进行仿真,得出相关结论,将本文算法的求解结果与其他文献算法的求解结果进行对比,证明本文GA-DDR调度算法对求解JSSP的有效性和优越性。
4.1 仿真环境
本节仿真实验在加速频率为2.20 GHz的Intel i5-4500U处理器、运行内存为4 GB的Windows 7 PC平台进行,采用Python语言编写,编译环境为Python Jupyter,编译器版本为Python 3.7.3。为使本文的GA-DDR调度算法效果最佳,经过多次仿真测试,GA的实验参数中设种群规模为150,交叉概率初始为0.6,变异概率初始为0.02(程序中第1次交叉变异概率取值为0.6和0.02,后续为动态变化),终止迭代次数为800。
4.2 LA06算例研究
本节GA-DDR调度算法中嵌入的DRs是类似于2.4节“If Job1_weight_higher=True and Job1_release_earlier=True,then Job1_first=True”的DR。因为性能指标为“最小化最大完工时间”,所以某一工序的加工时间Processing Time属性尤为重要,因此本节采用“If Job1_processing_lower=True, then Job1_first=True”这一DR对GA进行更新优化。
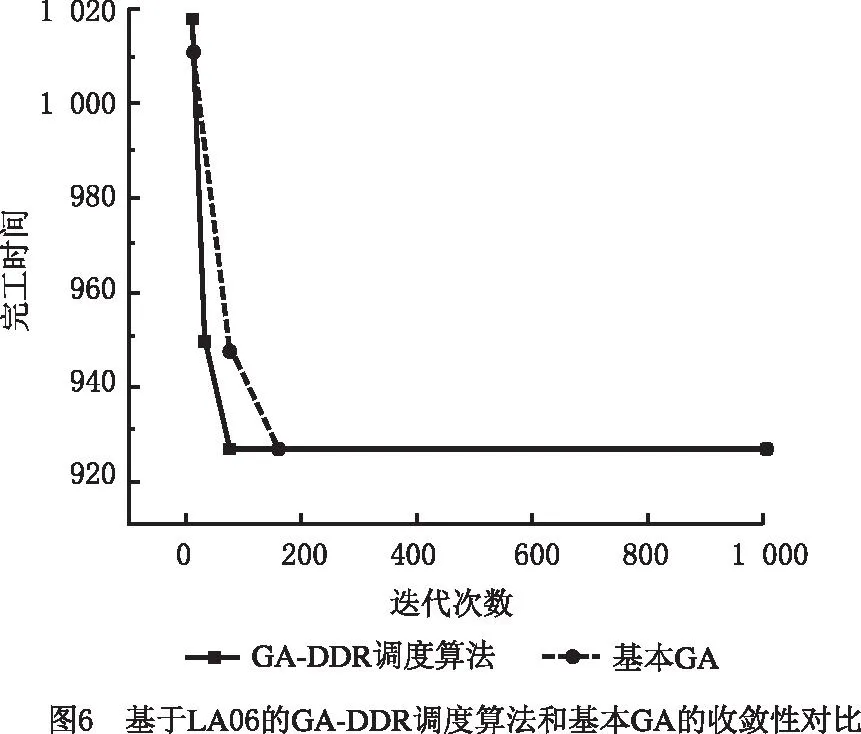
表7所示为LA06算例的工艺顺序约束和加工时间,例如第1行数据表示工件1先在机器2上加工21个单位时间,然后在机器3上加工34个单位时间,再在机器5上加工95个单位时间,以此类推,最后在机器4上加工55个单位时间。
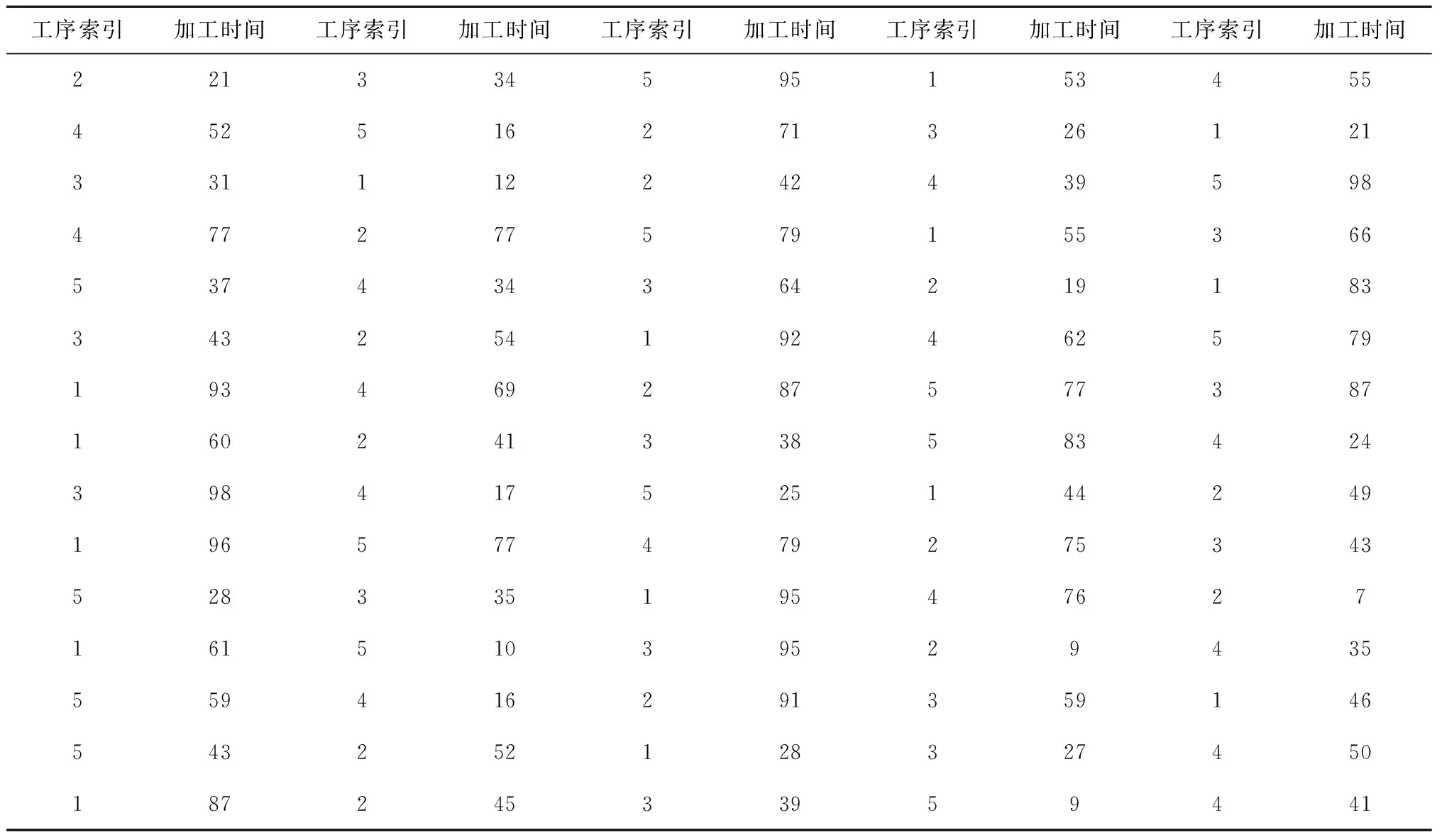
表7 LA06(15×5)的工件加工信息
由表7可得该算例的机器约束矩阵Tm和加工时间矩阵Tt,机器约束矩阵的转置矩阵
(16)
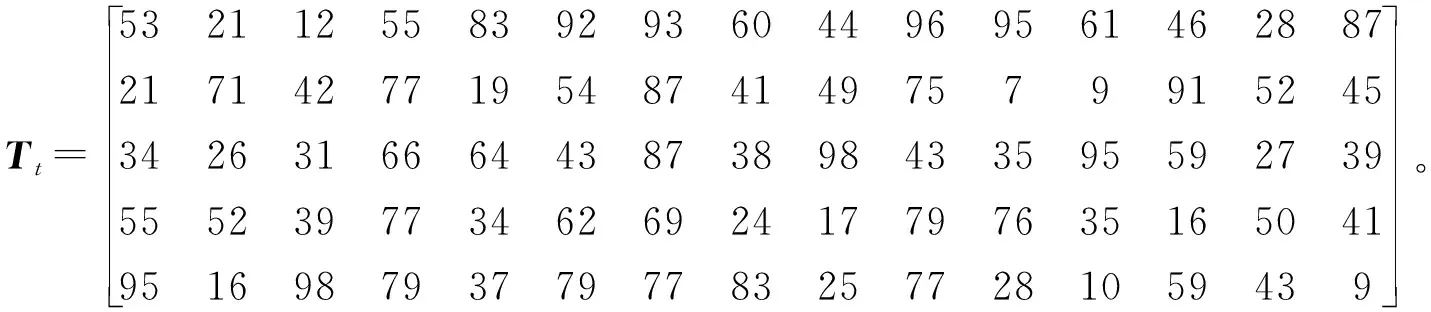
(17)
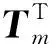
GA-DDR调度算法和基本GA分别求解LA06算例获得的最大完工时间收敛曲线对比如图6所示。可见,GA-DDR调度算法和基本GA最优调度的最大完工时间均为926个单位时间,但GA-DDR调度算法仅需73代便可以获得实验的最优解,而未嵌入DRs的基本GA在第157代才获得最优解,说明嵌入DRs后,原算法的收敛性大幅度增强,进一步提高了性能。因此GA-DDR调度算法具有较强的搜索能力,具备求解JSSP的能力。
4.3 LA11,LA17,LA24,LA26,LA33算例研究
首先采用LA01(10×5)算例作为调度数据集,通过挖掘LA01算例得到相应的DRs,将挖掘的DRs库应用到LA11(20×5),LA17(10×10),LA24(15×10),LA26(20×10),LA33(30×10)的大规模算例中验证GA-DDR调度算法的有效性。
(1)选择调度样本集
基于CART树的DRs提取步骤如下:①选择表8所示的LA01作为待挖掘调度数据;②对静态的调度数据集进行数据挖掘;③将挖掘的DRs应用到基本GA中,进一步求解JSSP。以上3个步骤组成了“DRs挖掘,调度优化,车间管理”的调度过程。
表8 LA01(10×5)的工件加工信息
(2)数据的表示
根据表8所示的LA01算例中的加工数据、工艺约束和“最小化最大完工时间”性能指标,选取常规的加工时间最短优先(Shortest Processing Time first,SPT)、剩余总加工时间最短优先(Least Work Remaining first,LWR)和总剩余工序数最少优先(Least Operations Remaining first,LOR)3个DRs组成算例历史DRs库,从而确定属性、属性值和类别值,如表9所示。

表9 属性、属性值和类别值
对于在同一台设备上等待加工的多道工序,分别比较其PT,RPT,ROPN的属性值,再经过预处理后,得到如下新属性:
1)Job_pt_longer 同一机器上两个任务的两道工序谁的加工时间更长。
2)Job_rpt_longer 同一机器上两个任务的两道工序谁的剩余加工时间更长。
3)Job_ropn_more 同一机器上两个任务的两道工序谁的剩余工序数更多。

表10 O21和O51的加工信息示例

表11 O21和O51的加工信息离散化处理
(3)构建数据集


表12 样本训练集
(4)规则调度决策树
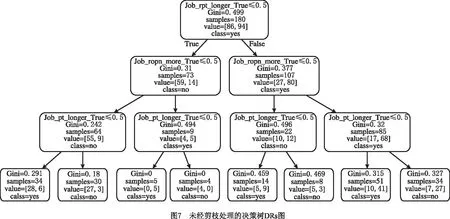
将表12的样本训练集读取到Python jupyter编译环境下。首先,将其按4∶1分为训练集和测试集(train_size=0.8);其次,在样本训练集中运用CART树生成CART树状DRs,将生成的DRs应用到测试集,观察该规则是否满足测试集,满足则该DRs库为本算例需要的DRs库,否则根据网格搜索法对此时的CART树进行后剪枝,直到生成的规则满足测试集,此时挖掘出的便是最佳DRs。图7所示为未经剪枝的决策树DRs图。
为了更加具体地展示图7所示决策树的形成过程,给出基于Python语言的决策树生成的程序代码,如图8所示。

图9所示为经过多次剪枝的最佳决策树DRs图。
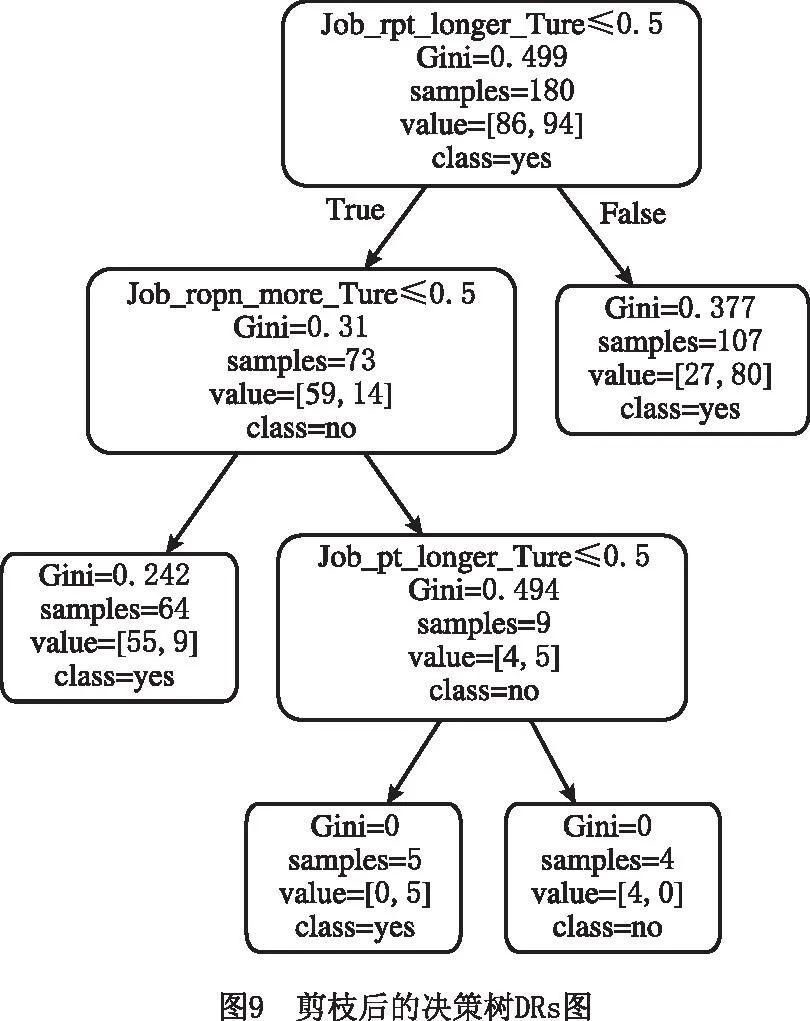
在图9的最佳决策树DRs中,因为CART树是二叉分类树,且每个属性值均小于等于0.5,所以真实规则的True和False正好相反,得到以下组合DRs:
1)If Job_rpt_longer=True, then Job_Oi1=yes(工序1先加工)。
2)If Job_rpt_longer=False and Job_ropn_more=False,then Job_Oi1=yes。
3)If Job_rpt_longer=False and Job_ropn_more=True and Job_rpt_longer=False,then Job_Oi1=yes。
4)If Job_rpt_longer=False and Job_ropn_more=True and Job_rpt_longer=True,then Job_Oi1=no(工序1后加工)。

为了更加具体地展示图9所示的剪枝后决策树的形成过程,给出基于Python语言的剪枝后决策树生成程序代码,如图10所示。

(5)GA-DDR调度算法求解结果
在挖掘出DRs的基础上,将上述DRs嵌入GA,便可得到本文所提GA-DDR调度算法。对LA11,LA17,LA24,LA26,LA33应用该算法,并与基本GA的仿真计算结果进行比较,结果如表13所示。图11~图15所示分别为5个算例基于GA-DDR调度算法的调度结果以及各个算例中GA-DDR调度算法和基本GA的最优解收敛曲线对比。
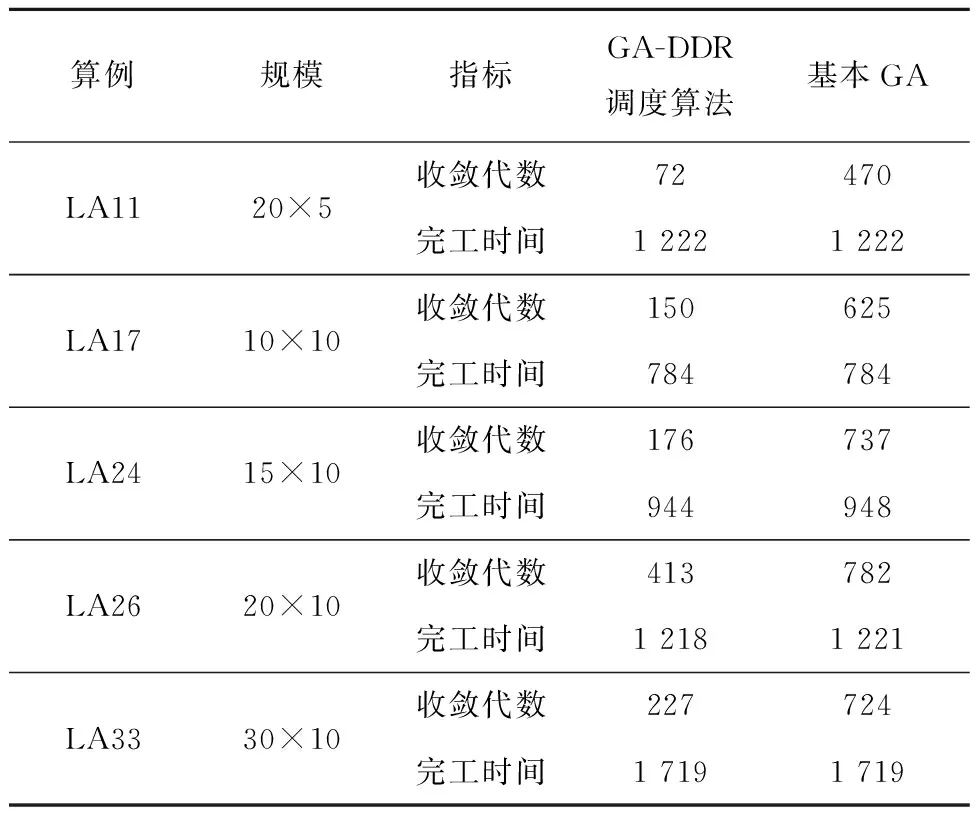
表13 算例求解结果
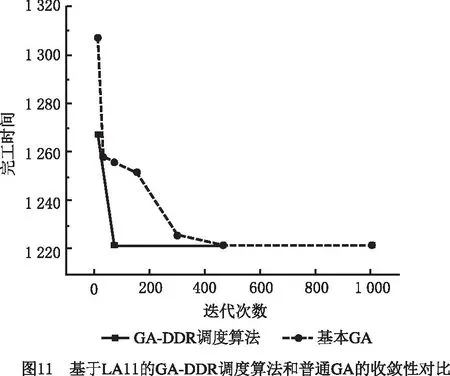
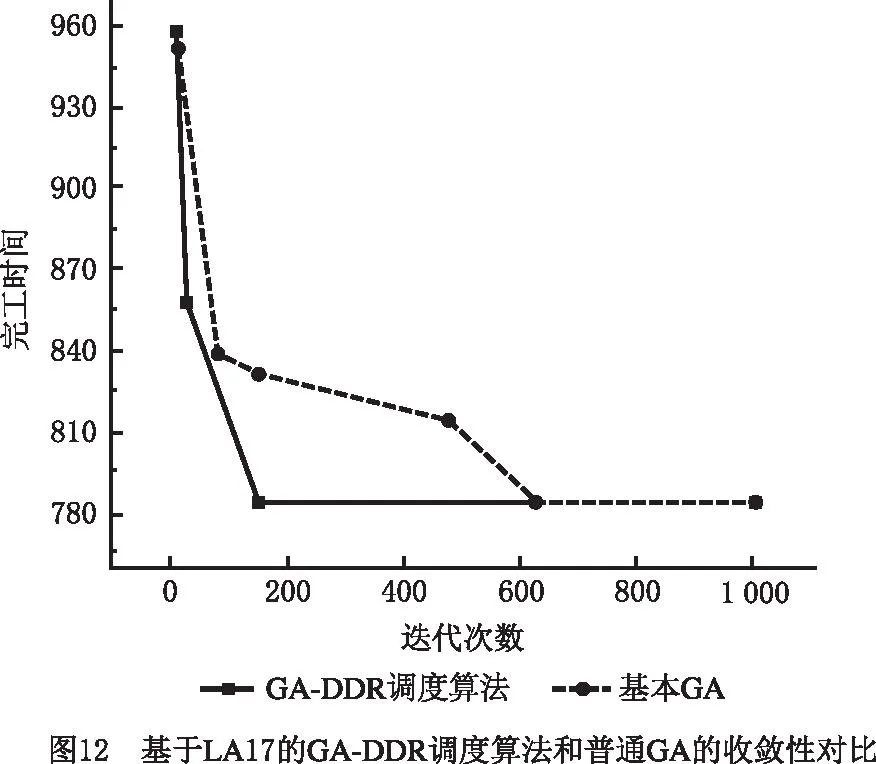
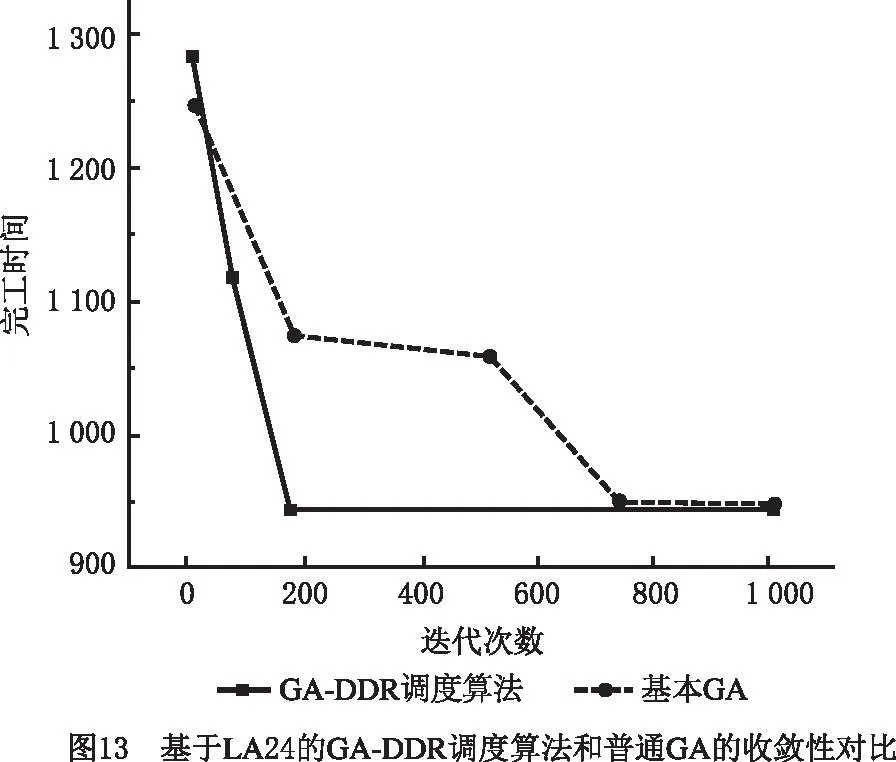
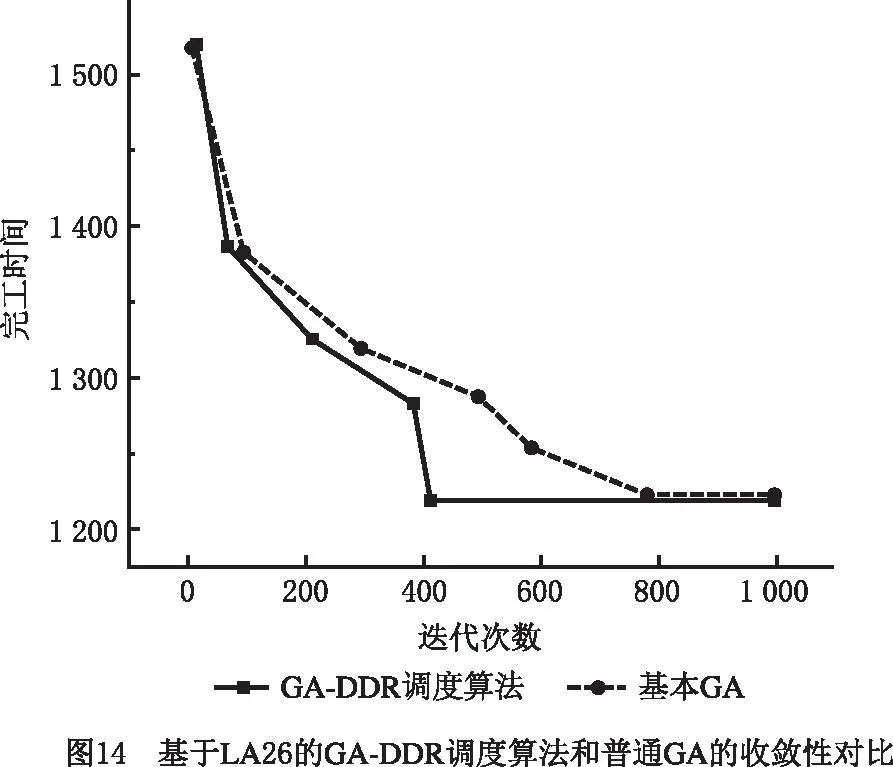
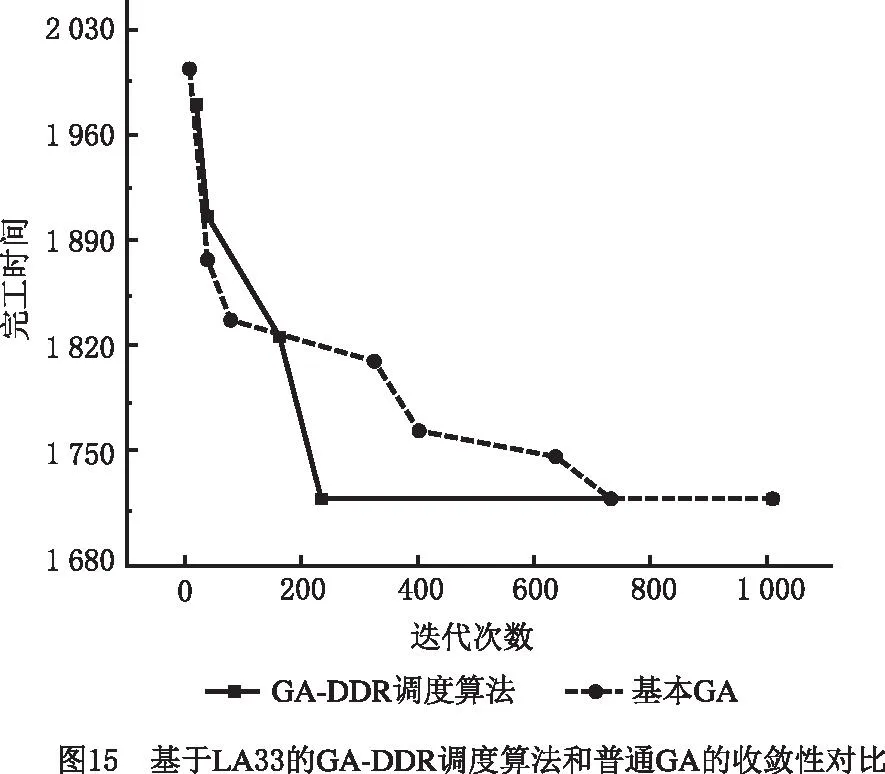
从图11~图15和表13可见,相比基本GA,GA-DDR调度算法均较早求解出了JSSP的最优解。因此在嵌入挖掘出的DRs后,基本GA的求解速度大幅度增强,收敛性也获得了提高,进一步证明了使用GA-DDR调度算法在求解较大规模JSSP中具有切实的可行性和高效性。
为了更加直观地展示GA-DDR调度算法的生成过程,给出基于Python语言的GA-DDR调度算法的程序代码,如图16所示。

4.4 多个LA算例研究
为了进一步验证GA-DDR调度算法的普适性和准确性,本节用多个Benchmark实例对该算法进行验证,并采用从LA01算例中挖掘出的DRs。种群大小设置为200,每个算例用本文改进算法运行20次,算例结果取最优值,其中大部分算例仅需要迭代300次~500次,少部分算例需要迭代500次以上。
本文将GA-DDR调度算法与基于混合遗传算法(Hybrid Genetic Algorithm,HGA)的调度算法[18]、基于粒子群优化(Particle Swarm Optimization,PSO)算法的调度算法[19]、GA(RM&COVERT)调度算法[20]和基于数据挖掘的DMA(data mining approach)调度算法[21]的仿真结果进行比较,如表14所示。
由表14可知,在实例规模较小的LA01~LA20中,各算法结果相差无几;当实例为规模相对复杂的LA21~LA40时,GA-DDR调度算法在大部分实例上的最大完工时间优于其他算法,其可以在搜索空间快速找到最优区域。由此得出结论:本文所提GA-DDR调度算法充分结合了DMA和GA的优势,即在基本GA的基础上嵌入挖掘出的DRs,从而增强了调度算法的搜索能力,并在求解质量和收敛性上均具有优势。
5 结束语
本文针对作业车间的生产数据具有离散性、多样性、复杂性和隐蔽性等特点,采用DMA中的CART树挖掘DRs作为有效的调度知识构建调度DRs库。在实施过程中,本文所提GA-DDR调度算法能够在不同JSSP实例中挖掘出不同的树状DRs,再将其与GA结合来求解更复杂的JSSP,并通过仿真实验测试证明了所提调度算法的有效性。未来拟进一步研究具有机器随机发生故障、多目标优化的JSSP及柔性车间的DRs提取等方面的问题,以提升调度算法的求解精度和收敛性等。
