质量感知的多目标云制造服务组合优化算法

刘桂森,贾兆红,2+

(1.安徽大学 计算机科学与技术学院,安徽 合肥 230601;2.安徽大学 计算智能与信号处理教育部重点实验室,安徽 合肥 230601)

0 引言

云制造3.0系统为制造业与信息通信技术的深度融合提供了智能制造系统新模式[1]。云制造融合了网络化制造和服务、云计算、高性能计算、物联网等技术,实现硬件设备、计算系统、软件、数据、知识等分类资源的统一制造、集中管理和运营,为制造全生命周期过程提供可随时获取、按需使用、安全可靠、优质廉价的各类制造服务,是一种面向服务的网络化制造模式[2]。

在云制造环境中,用户将制造任务提交到服务平台,服务平台通过分析任务复杂度分解任务,并根据用户需求从平台中选择符合的服务进行组合,以共同执行用户任务[3]。然而,云计算的服务提供商不断提供功能相似但质量不同的云服务[4],如何在大量云服务中选择组合以满足用户的服务质量(Quality of Service,QoS)期望,即QoS感知云服务组合(Quality of Service—Cloud Service Composition,QoS-CSC)问题[5],成为计算服务供应中的关键问题[6]。

例如,随着现代社会的发展,汽车的私人定制逐渐成为一种趋势。一款车包括基础、外部配置、内部配置、安全配置、特色配置5部分。基础部分包括汽车的发动机、变速箱、底盘三大件,是汽车的主要组成部分;外部配置包括天窗类型、行李架、轮毂等;内部配置包括方向盘、液晶仪表等;安全配置包括主动安全和被动安全;特色配置指车载冰箱、车内香氛装置等。汽车的每个模块及部件均有多家供应商,每家供应商提供的零部件都具有相同功能但功能属性不同,如成本、时间、可靠性、可用性、信誉度等QoS,如何从不同供应商中选择合适的厂家零部件,以完成汽车的私人定制,满足用户需求,是云制造服务组合(Cloud Manufacturing Service Composition,CMSC)的关键。

随着云环境中类似的单一服务越来越多,CMSC问题也成为NP-hard(non-deterministic polynomial—hard)问题[7]。由于数学模型的非线性特性以及大量的候选服务,采用线性和整数规划等精确方法通常不可行。BAO等[8]用有限状态机来规定Web服务的合法调用顺序,提出一种基于树修剪的改进算法来创建Web服务组合树,生成所有可行的执行路径后,采用简单加权技术选择最佳解决方案;CHEN等[9]将带有约束的多目标优化问题改成两个主要目标,即最小QoS风险(使QoS目标与用户约束之间的差异最小)和最大化QoS性能;JIAN等[10]提出改进的鸟群优化算法,在基本鸟群优化的基础上引入二阶震荡方程和鸟类的历史位置记忆来最小化服务组合的整体时间成本;ZHOU等[11]提出一种混合人工蜂群算法,将CMSC问题转变为双目标问题求解;LIANG等[12]将CMSC分为上升和下降的QoS标准,采用具有双重限制的服务选择模型进行优化;YANG等[13]提出一种增强型灰狼优化(Enhanced Multi-Objective Grey Wolf Optimizer,EMOGWO)算法,同时优化QoS与能源消耗两个目标。另外,遗传算法(Genetic Algorithm,GA)[14]、粒子群优化(Particle Swarm Optimization,PSO)算法[15]、MOEAQI(multi-objective evolutionary algorithm framework for service selection with QoS constraints and inter-service correlations)算法等也用于求解服务组合问题,但是这些算法往往通过加权组合将多目标问题简化为单目标问题,很少考虑同时优化4个或4个以上目标。在多维空间中平衡开发与探索面临诸多挑战[16],如非支配解的指数增长所带来的收敛压力损失[17],以及无效的多样性维持机制所导致的反收敛现象[18]。本文针对同时优化时间、成本、可靠性、可用性、信誉度的服务组合问题,提出一种基于自适应选择和反向学习策略的进化算法(Evolutionary Algorithm based on Adaptive selection and Reverse learning Strategy,ARSEA),首先根据QoS对服务进行聚类,剔除效果比较差的服务,其次为目标空间中的参考向量分配近邻和远邻参考向量,然后采用反向学习策略增加初始种群的多样性,在迭代过程中通过动态调整选择概率自适应选择参与交配的父代个体,以统一算法的多样性与收敛性。

1 问题描述

1.1 相关定义

在云制造环境下,不同于单一的制造任务,加工前为了提高产品质量,需将复杂的制造任务分解成多个子任务,根据每个子任务的功能需求生成多个候选服务CS,即一组功能相同但非功能属性不同的服务,构成相应的云服务集CSS,再从相应的候选云服务集中获得每个子任务的制造服务[19]。在此基础上,基于逻辑序列所选CS组成的组合制造服务(Composite Manufacturing Service,CMS)可以同时满足功能和QoS要求。因此,复杂制造任务的执行过程分为4个步骤:①分析请求和分解任务;②搜索和匹配;③组成服务和选择优化;④执行和反馈任务。针对步骤3,给出以下定义。

定义1复杂制造任务。ZT={T1,T2,…,Ti},ZT为复杂制造总任务,Ti为所分解的第i个子任务,i=1,2,…,n。

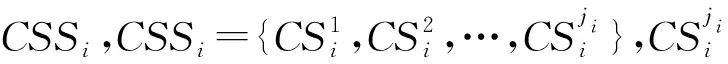
定义3服务质量。QoS={q1,q2,…,qr},QoS表示CS的非功能属性,如时间、成本、效率或可用性,qr为CS的第r个服务质量属性值,r=1,2,…,m。

其中,本文扩展了服务质量的属性个数。

1.2 服务质量模型

由于QoS由多个侧重于不同方面的非功能度量组成,很难有所有度量值同时最佳的解决方案,往往采用一组各度量值相互权衡的Pareto最优解,即改进其中一个度量值可能导致其他度量值恶化。例如,时间和成本通常是一对相互矛盾的属性,缩短时间可能增加成本。鉴于可测量性的重要性,本文针对CMSC的顺序、平行、选择和循环4种基本复合结构,研究不同结构复合服务的聚合QoS公式(如表1),对这5个QoS进行组合评估,使整体QoS值达到最优以满足用户要求。对5个属性指标的描述如下:

表1 不同结构复合服务的聚合QoS公式

(1)时间 从用户提交制造任务到该任务完成并返回结果的时间。

(2)成本 当所执行的云制造服务完成后,服务提供商向用户收取的服务费用。

(3)可靠性 在给定的时间和条件下,成功执行制造任务的能力。

(4)可用性 在云制造服务平台中,用户在一定时间内成功调用制造服务的能力。

(5)信誉度 指服务提供商完成该制造任务的信誉履约度。

根据文献[15],可以将平行结构、选择性结构和循环结构转化为顺序结构。另外,由于聚合QoS标准值尺度不同会严重影响基于分解的多目标进化算法(Multi-Objective Evolutionary Algorithm,MOEA)标度函数,所有聚合的QoS值均在[0,1]内归一化。可靠性、可用性、信誉度属于正属性,时间和成本属于负属性。对于QoS的正属性,较大的值性能更好;对于负属性,较小的值性能更好。正准则和负准则的归一化方法如下:

(1)

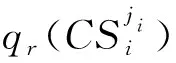
Q(qosr(x)=(Q1(qos1(x)),Q2(qos2(x)),Q3(qos3(x)),
Q4(qos4(x)),Q5(qos5(x)))。

s.t.

x∈Ω。

(2)

其中:Q1～Q5分别表示时间、成本、可靠性、可用性和信誉度指标;Ω表示决策空间。

2 ARSEA算法

2.1 算法框架

本文所提的ARSEA算法流程如下:

算法1ARSEA框架。

输入:种群规模N、权重向量的邻居向量个数H、初始交配选择的概率Q、间隔代数L、变异概率P。

输出:归档种群EP。

步骤1过滤候选服务。

步骤2在目标空间中生成均匀的参考向量,并为每个参考向量确定其近邻参考向量和远邻参考向量。

步骤3种群初始化。

步骤4采用反向学习策略进一步优化初始种群。

步骤5迭代:

(1)对种群中的每个个体采用选择策略,然后交叉、变异得到新个体Y,更新近邻解。

(2)将种群中的非支配个体加入归档种群EP,并更新归档种群EP。

(3)采用概率更新策略改变交配选择概率。

首先采用K-means聚类过滤候选服务;然后在目标空间生成一组均匀的参考向量,根据向量之间的余弦角度找出每个向量的近邻向量和远邻向量;其次,将初始化种群中的个体与参考向量一一对应。步骤4采用反向学习策略生成反转的种群,通过比较反转种群与原初始种群产生最终的初始种群,以提高种群的多样性。在迭代搜索过程中,先通过选择策略从父代选出优秀个体参与交配,再根据Pareto方法从新生个体与其他个体中选择较优的解放入归档种群EP,根据新解的贡献度自动更新父代选择概率来平衡全局开发与局部探索。

2.2 过滤候选服务

随着智能制造的高速持续发展,云制造平台中的服务越来越多,在CMSC的方案中,可供选择的候选服务也越来越多,需要根据候选服务的QoS对服务进行选择过滤以缩短求解时间,而聚类方法有助于提升服务选择的效率。K-means聚类按照类内相似度最大化和类间相似度最小化原则对数据样本进行分组,是最常用的无监督聚类方法之一。因此本文基于K-means对候选云服务集进行聚类,并对候选服务进行等级划分,在得到的每一簇中去除等级最差的候选服务,如算法2所示。

算法2过滤候选服务。

输入:决策空间信息S1、聚类的簇数Nc(默认与目标数一致)。

输出:决策空间信息S。

步骤1随机选择Nc个候选服务作为簇的中心。

步骤2对于每一个簇,计算簇的质心。

步骤3对于每个候选服务,计算其与Nc个簇质心的欧式距离,将其加入距离最小的簇中。

步骤4再次计算各个簇的质心,如果质心位置不变,则执行步骤5,否则转步骤3。

步骤5对每一个簇中的候选服务,采用式(3)计算函数d并进行排序,剔除本簇后10%的候选服务。

2.3 反向学习策略

由于CMSC为NP-hard问题,在算法初始阶段采用如算法3所示的反向学习策略改进初始种群在解空间的分布,以提高算法的多样性。首先,在每个子任务候选云服务集中计算每个候选服务与最优服务之间的距离

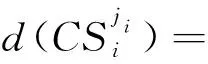
(3)

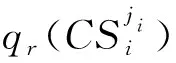
算法3反向学习。

输入:初始种群P1、决策空间信息S。

输出:种群P。

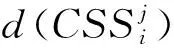
步骤2对P1中的每个体,计算每个候选服务在上述排序中的位置,选择其相反位置的候选服务组成新的个体。

步骤3由新的个体组成新的初始种群P2。

步骤4利用切比雪夫法则比较并保留较优的个体,得到最终的初始种群P。

2.4 选择策略及概率更新策略

本文采用算法4所示的选择策略。在选择父代重组交配时,相近个体间交配有利于算法的局部开发能力,较远个体间交配有利于算法的全局探索能力,而且在选择相近个体时,从其近邻范围内的非支配个体中挑选父代更有利于算法收敛。另外,通过自适应改变交配选择概率,算法可以自动调整搜索方向。

算法4选择策略。

输入:初始交配选择的概率Q。

输出:交配父代x1,x2。

步骤1如果产生的随机数大于Q,则随机选择其远邻向量对应的个体作为x1,x2。

步骤2如果产生的随机数小于等于Q,则先确定其近邻向量对应的个体群中非支配解的个数n,如果n>2,则随机选择个体群中的非支配个体作为x1,x2,否则随机选择个体群中的个体作为x1,x2。

在种群进化过程中,算法进行全局和局部搜索的需求是可变的,因此本文采用如图1所示的概率更新流程图更新交配选择概率,以平衡算法的开发和探索能力。早期需要提高算法的全局探索能力,随着迭代的进行需要更好的局部开发能力,因此为了在开发和探索之间取得平衡,采用式(4)自适应地调整交配概率,使算法间隔一定代数后,可以自动调整Q的大小,其中n1和n2分别为前L代种群中由近邻和远邻交配产生的新个体数。

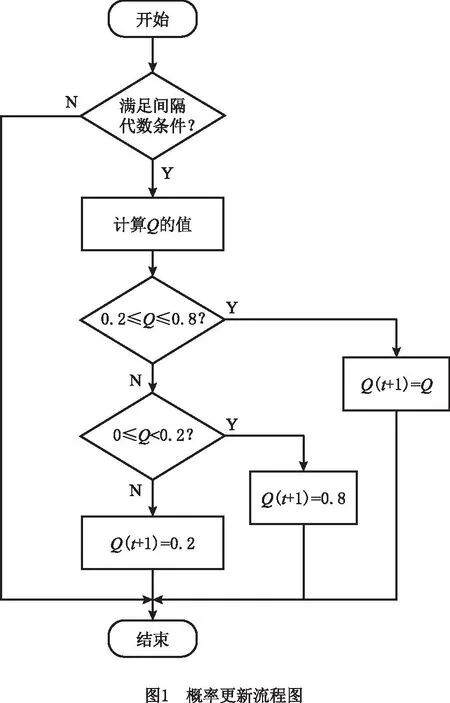
(4)

2.5 算法的时间复杂度分析

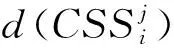
3 仿真实验及结果分析

为了评估所提ARSEA的性能,选用4种对比算法,即具有对抗性搜索的自适应双种群进化算法(Adaptive Dual-population evolutionary Paradigm with Adversarial Search,ADPAS)[20]、EMOGWO算法、基于支配和分解的多目标进化算法(Multi-Objective Evolutionary Algorithm based on Dominance and Decomposition,MOEA/DD)和基于参考向量引导的多目标优化进化算法(Reference Vector guided Evolutionary Algorithm for many-objective optimization,RVEA)[21],其中ADPAS和EMOGWO是两种解决CMSC最先进的算法,MOEA/DD和RVEA是两种最新提出的经典MOEA。另外对ARSEA的策略进行了验证。

3.1 实验设计

采用15个随机生成的测试算例验证ARSEA在各种条件下的探索和开发性能,算例的因素和取值范围如表2所示。每个实例由工作流中的子任务和候选服务组成,代表不同的CMSC场景。优化目录m的数量设置为5,子任务和候选服务分别记为T和S,例如T20S60表示有20个子任务,每个子任务有60个候选服务、5个优化目标。

表2 算例的因素和取值范围

每个候选服务均有时间、成本、可靠性、可用性、信誉度QoS标准,并随机生成一个综合QoS数据集,其取值范围如表3所示。所有算法均使用C++编程,在Core i5、3.40 GHz处理器和16 GB RAM的Windows 10 PC上运行。

表3 QoS数据取值范围

3.2 参数设置

采用田口法为ARSEA选取合适的参数。ARSEA考虑的主要参数包括交配选择概率的更新代数L、邻居向量的个数H和变异概率P,取值范围如表4所示。根据田口法设计了9个参数组合实例组,如表5所示。

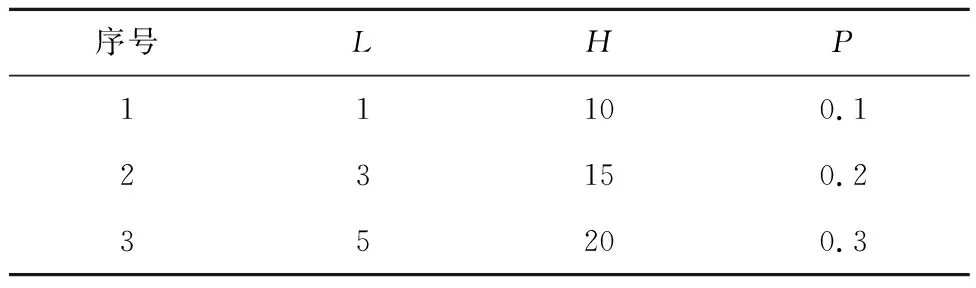
表4 ARSEA参数取值范围

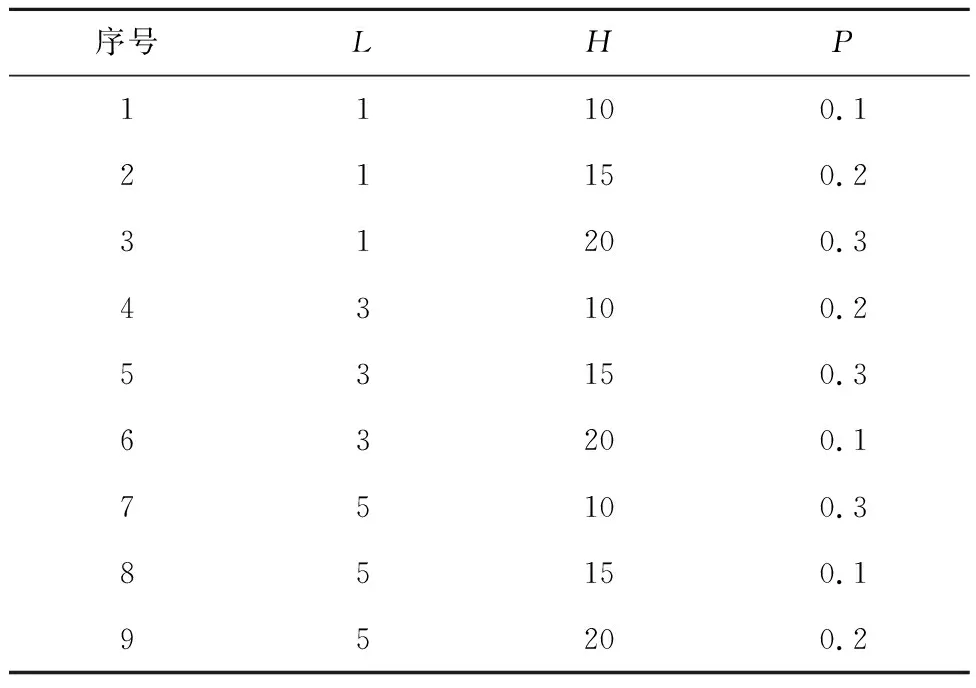
表5 参数组合

采用反转世代距离IGD评估具有不同参数组合的ARSEA性能,用15个测试实例中每个参数组合的ARSEA的平均IGD值作为响应变量,在MINITAB 19版本上运行。实验结果如图2所示,其中x轴表示不同因素对应的水平,y轴表示均值响应值,平均值越小表示对应组合参数的ARSEA效果越好。从图2可见,最佳参数值为L=3,H=15,P=0.1。

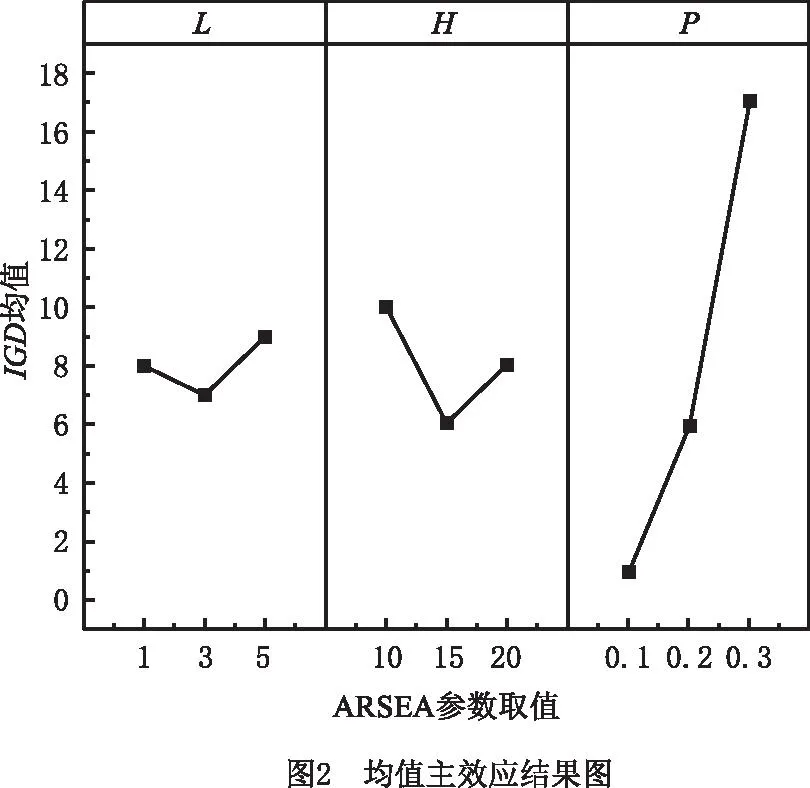
ARSEA其他参数的设置与4种比较算法相同,即种群规模N=126,交叉概率设置为1.0,迭代次数为500。初次交配选择的概率P1=0.3,以确保搜索开始时ARSEA具有更好的勘探能力。对于每个实例,每个算法重复运行30次,取其平均值作为最终的统计结果。

3.3 评价指标

采用如下3个评价指标:

(1)非支配解集规模NNS表示每种算法获得的非支配解决方案的数量,获得的非支配解决方案越多,为决策者提供的选择越多,算法的多样性也就越好。

(2)反转世代距离IGD描述非支配解集与Pareto边界的接近程度,用于评估解集的收敛性和多样性[22],定义为

(5)

式中:υ为某一种比较算法获得的非支配解集;ρ为所有算法获得的非支配单个集合的并集。IGD值越小,算法的收敛性和多样性越好,越接近真实的Pareto前沿。

(3)间距度量Spacing反映非支配解集前沿分布的均匀性[23],定义为

(6)

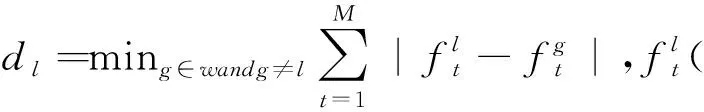
3.4 实验结果

ARSEA中采用的策略包括反向学习策略、选择策略和概率更新策略。首先设计ARSEA的变体验证所提策略的有效性,其次将ARSEA与其他先进算法进行比较。在表6～表10中,第1列均为实例编码,每个实例组的最佳结果用粗体显示。

3.4.1 反向学习策略的性能

本文设计了不含反向学习策略的ARSEA变体ARSEA-NRL(ARSEA-non-reverse learning)与ARSEA进行比较,结果如表6所示。

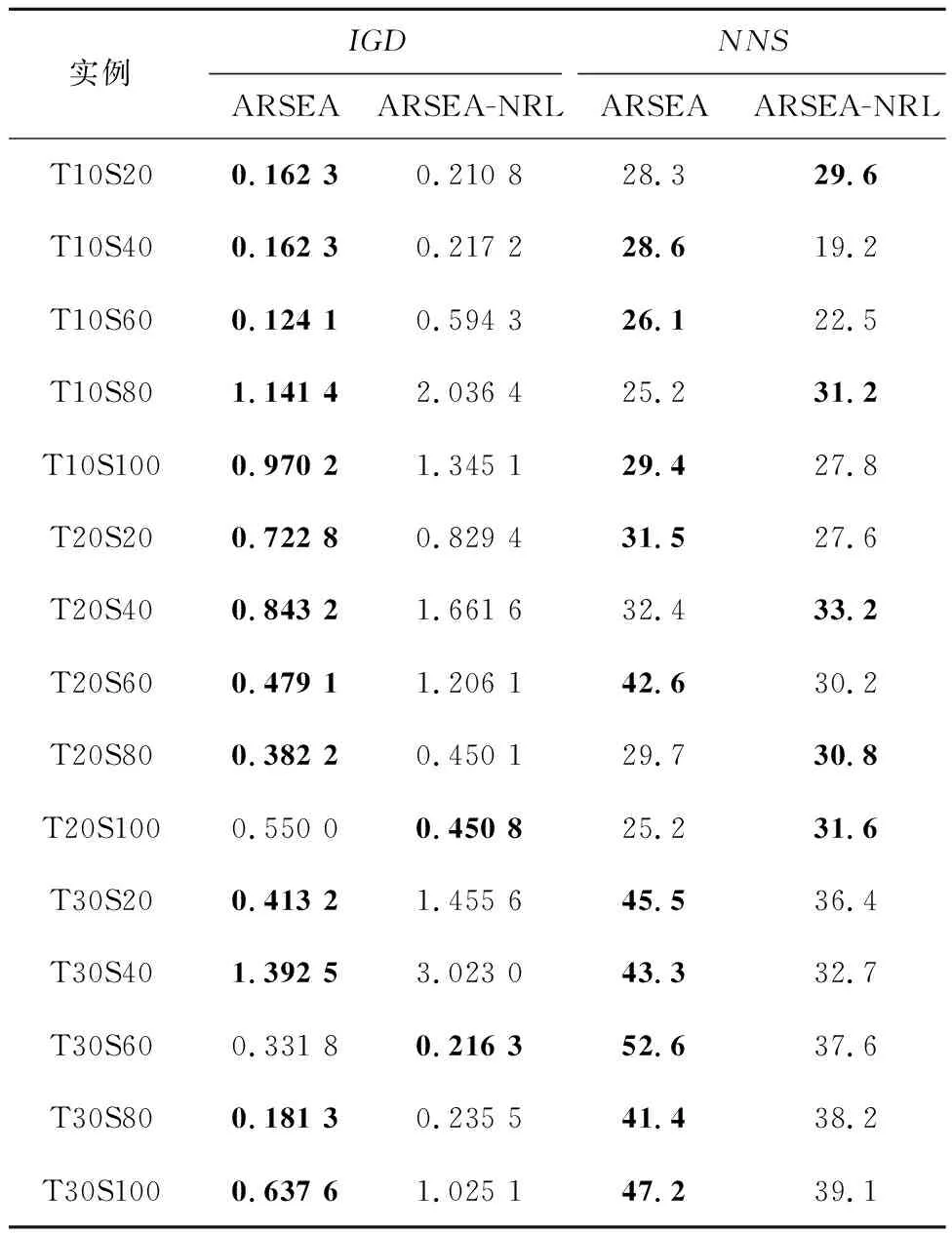
表6 在IGD和NNS下反向学习策略的验证实验结果

从表6的NNS值可见,ARSEA-NRL在5个实例上胜过ARSEA,ARSEA在其他10个实例上可以获得更多的非支配解,而且ARSEA在大规模服务组合问题上的优势更加明显。另外,从IGD值可见,ARSEA明显优于ARSEA-NRL,说明ARSEA的解质量更好,更接近问题实际的Pareto前沿,表明所提反向学习策略有益于提高算法性能。

3.4.2 选择策略的性能

设计采用随机选择方法的ARSEA变体ARSEA-R(ARSEA-random)进行验证,实验结果如表7所示。

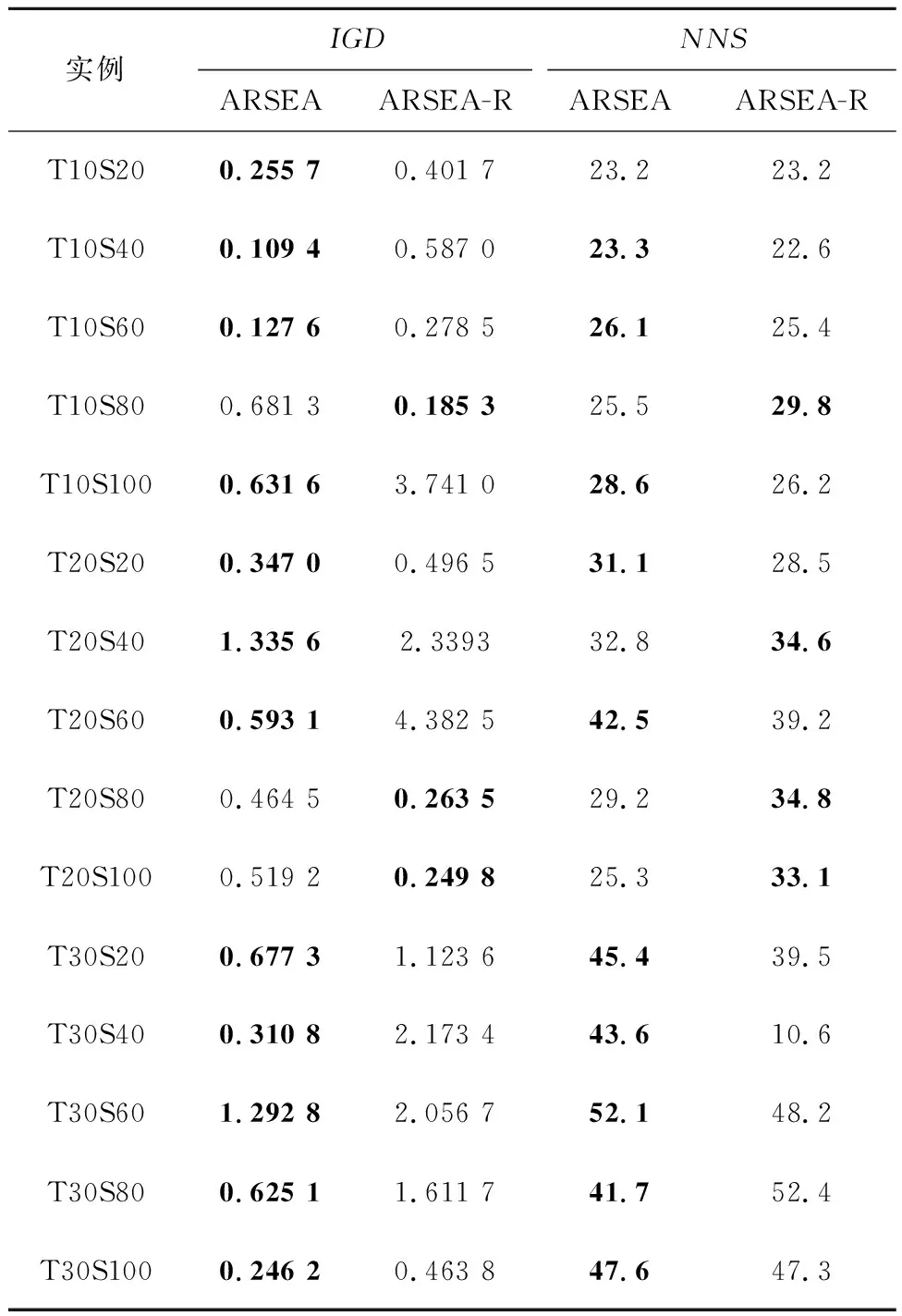
表7 选择策略的验证实验结果

从表7可见,ARSEA在IGD和NNS上分别有3个实例稍逊于ARSEA-R,而在其他10个实例上,ARSEA全部优于ARSEA-R,表明ARSEA不但能够找到质量更好的解,而且能够帮助算法提高解的多样性。

3.4.3 概率更新策略的性能

将ARSEA算法中的选择概率分别设置为固定值0.2,0.5,0.8,对应算法分别记为ARSEA-A,ARSEA-B,ARSEA-C,实验结果如表8所示。

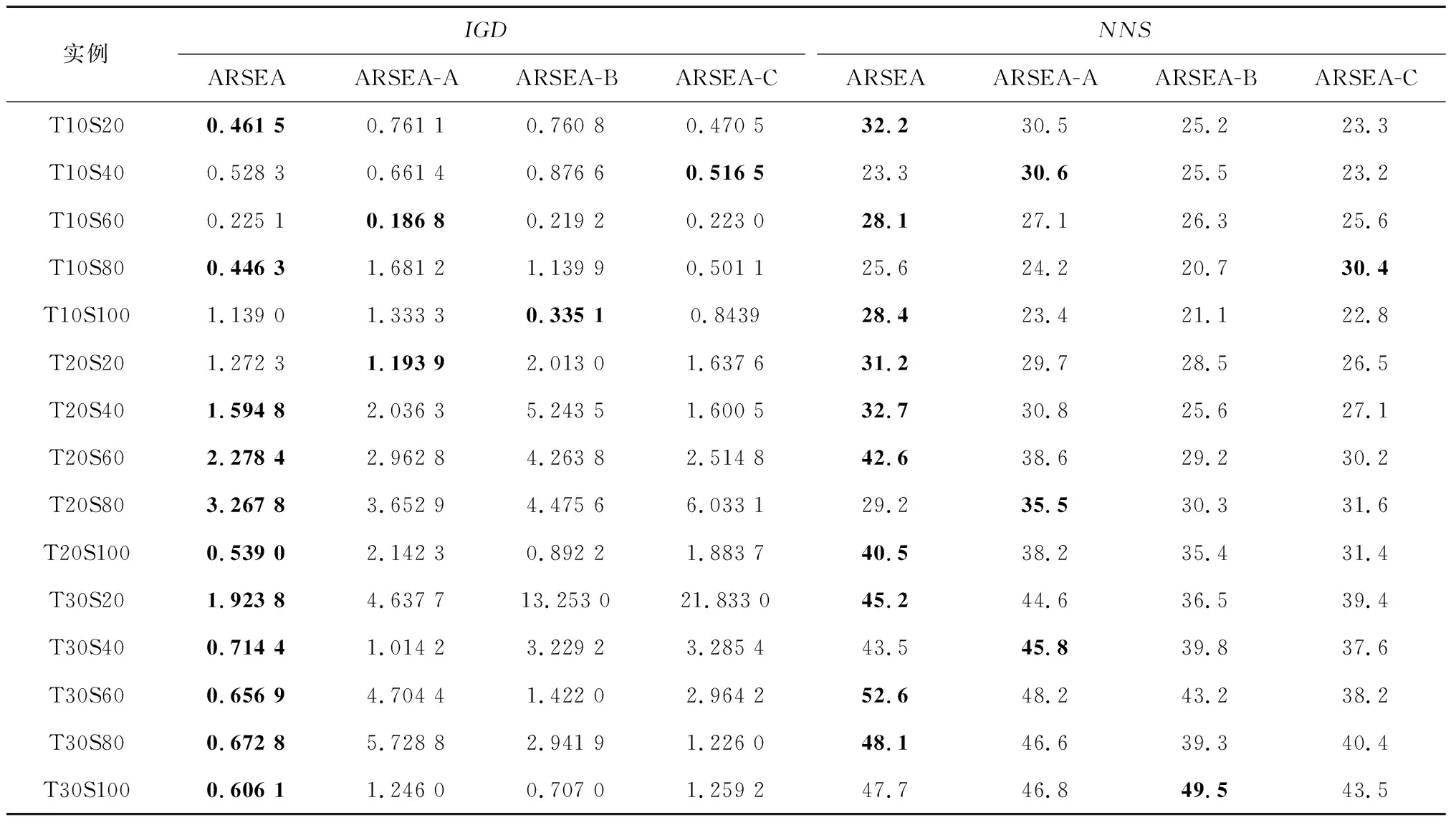
表8 概率更新策略的验证实验结果

由表8可见,ARSEA在10个实例上的NNS值较大,其他3个变体在5个实例上具有优势,说明ARSEA可以在大部分实例上找到更多的非支配解。虽然在小规模服务组合问题中,ARSEA的IGD值较其他算法没有明显优势,但是在较大规模实例上的结果都是最好的,表明自适应调整选择概率可以在算法的开发和探索之间取得更好的平衡。

3.4.4 算法整体性能比较

4种对比算法与ARSEA的比较结果如表9和表10所示。

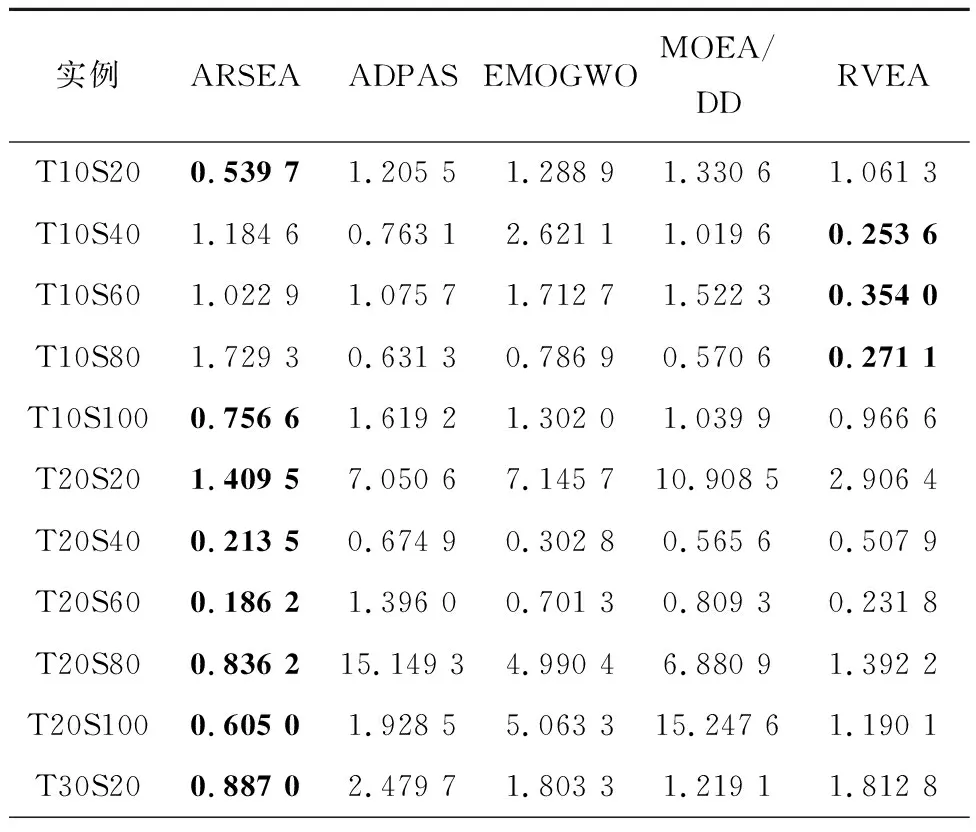
表9 5种算法的IGD比较结果

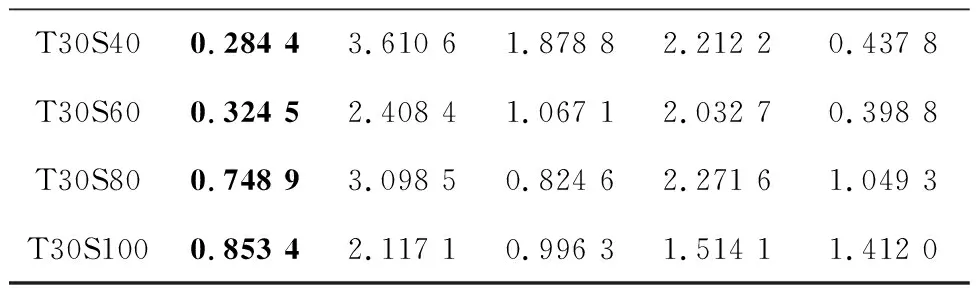
续表9

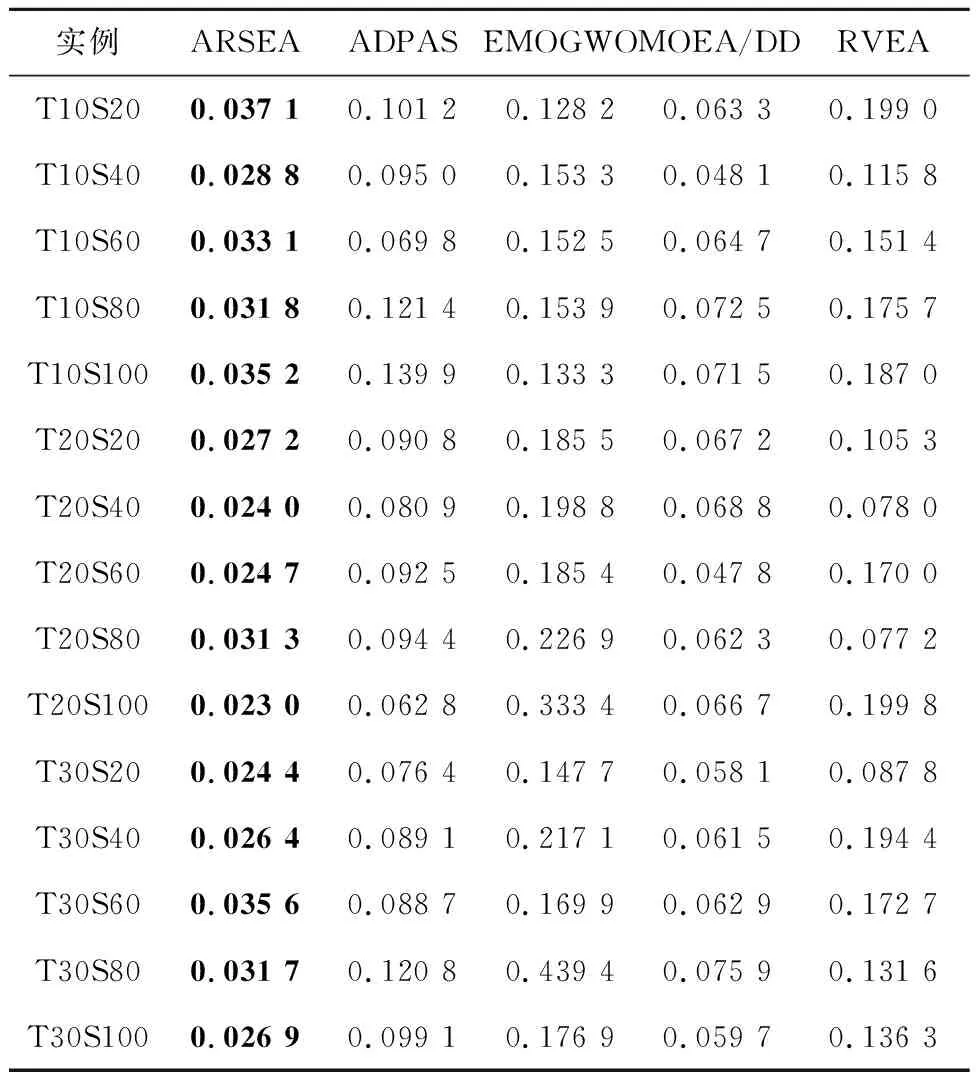
表10 5种算法的间距度量Spacing比较结果

由表9可见,虽然在3个小规模的服务组合实例中,ARSEA的结果不如其他算法,但是其他实例上ARSEA的结果都是最好的,表明ARSEA在求解CMSC上能够找到更多且质量更好的解。由表10可见,ARSEA在所有测试实例上的Spacing值最小,说明ARSEA找到的解分布更均匀,多样性更好。

为了直观地比较5种算法的性能,图3～图5展示了5种算法的IGD、Spacing值和计算时间的对比结果。ARSEA的计算时间最少,其在图3中的IGD平均值最低,在图4中的曲线最靠下,表明在收敛性和多样性上ARSEA较其他4种算法都具有绝对优势。

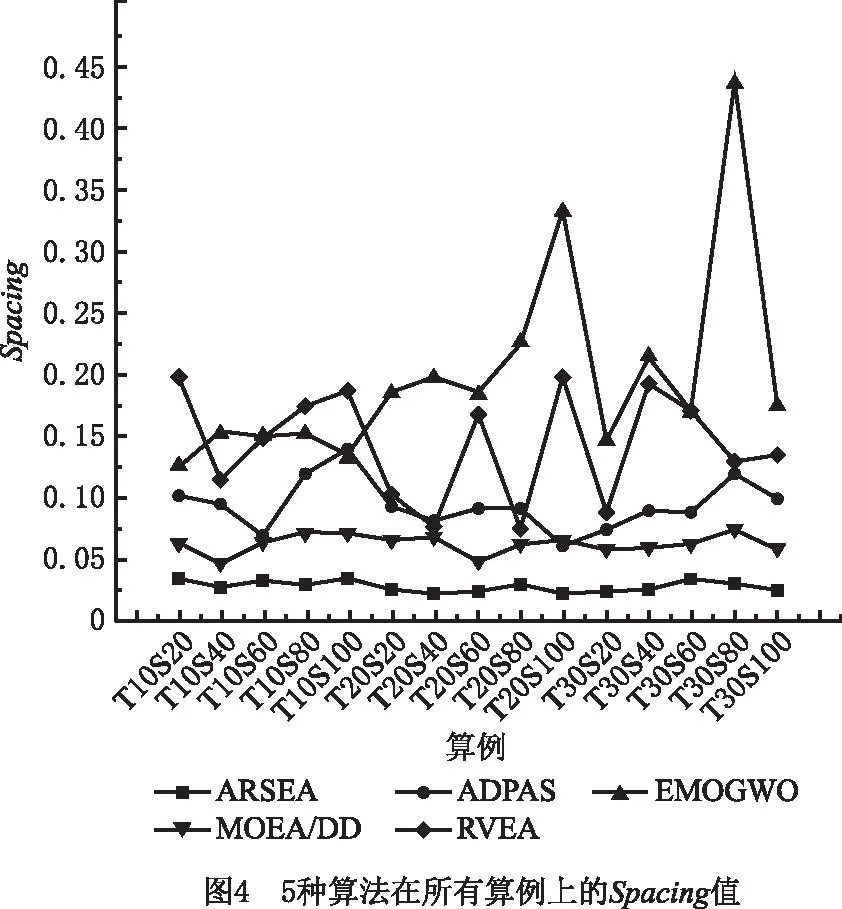
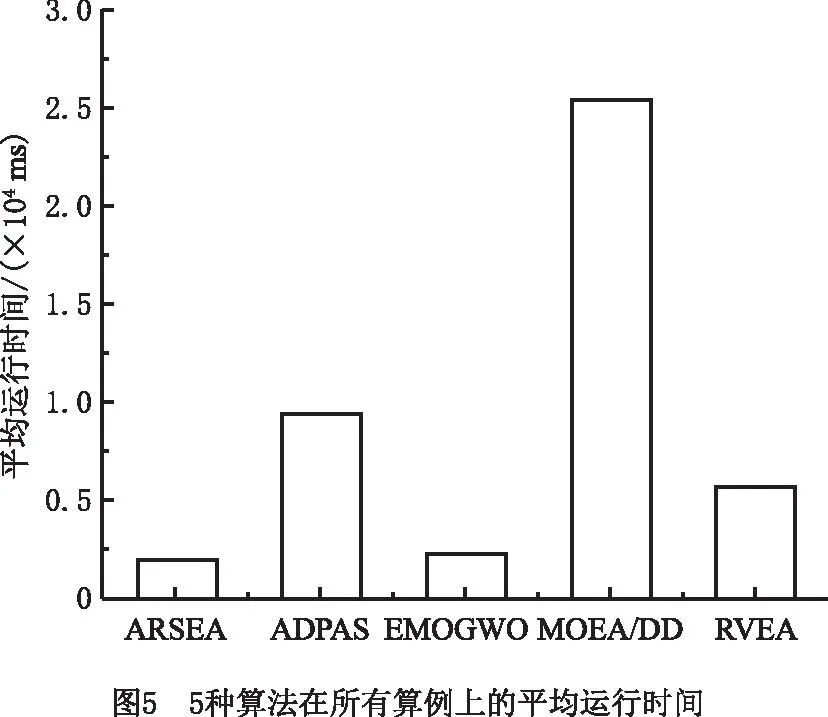
较低的S值表明ARSEA得到的归档种群在Pareto前沿上的分布更加均匀,各个目标之间比较平衡,多样性更好;较低的IGD值表明ARSEA得到的解的收敛性和多样性较好,说明ARSEA在CMSC 5个目标同时优化问题上可以得到较好的解决方案。而且,ARSEA求解服务组合方案的用时最少,说明ARSEA中过滤候选服务的方法很适合解决具有大量候选服务的CMSC问题。从实验结果整体来看,ARSEA比其他算法在CMSC问题上得到的解更接近问题真实的Pareto前沿,而且解的均匀性更好。算法求解多目标CMSC问题得到的每个非支配解,经过解码后都是一种制造服务的组合方案,用户可以根据需要选择归档种群中的方案执行制造服务,使组合服务的整体QoS达到最优。

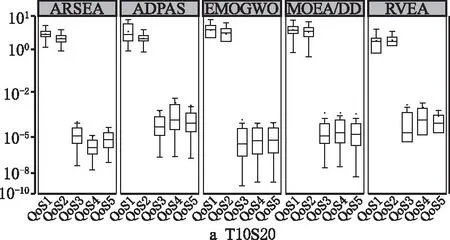
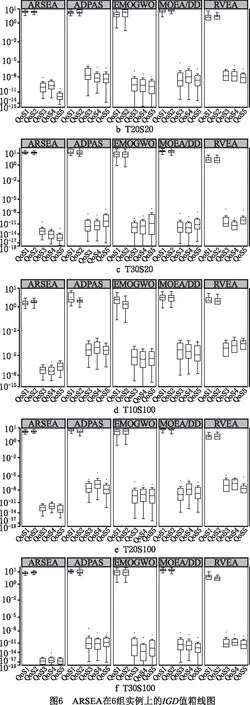
从15组实例的每种子任务中各选2组,组成6组实例,绘制出ARSEA在这6组实例上IGD值的箱线图,如图6所示,其中每组图中x轴分为5组,每组代表的算法分别是ARSEA,ADPAS,EMOGWO,MOEA/DD,RVEA,每组x轴下方是服务组合的5个属性,通过这些图可以明显看出5个算法之间的差异,ARSEA虽然在部分算例的前两个属性指标上稍差,但是另外3个属性指标值远小于其他对比算法。因此,综合图3和图4可以看出,ARSEA的整体性能较好,其可以获得更好的解决方案。

在汽车的私人定制过程中,用户可以选择自己的个性化零部件,每个零部件都有若干服务提供商,这些服务提供商具有相同的功能属性和不同的非功能属性(如时间、成本、可靠性等)。从不同供应商中选择合适的厂家生产零部件来完成汽车的私人定制,使非功能属性最优,是一个多目标CMSC优化问题,可以采用ARSEA解决该问题。ARSEA的求解时间最少,效率最高,所求得的非支配解集的多样性和收敛性较好,即汽车私人定制的解决方案数最多,给用户的选择最多,其求得的解决方案在整体QoS上优于其他算法。因此,采用ARSEA选择合适的供应商生产零部件,使用户整体的时间、成本、可靠性等最优,用户满意度最高。

4 结束语

本文从多目标优化的角度研究CMSC问题,提出基于自适应选择和反向学习策略的进化算法ARSEA,采用K-means聚类剔除较差的候选服务,采用反向学习策略增加种群的多样性,将参考向量分为近邻和远邻参考向量,利用选择策略和自适应调整的概率更新策略更好地平衡算法的开发与探索性能,从而为用户提供更为优质的服务组合。随着全球生态环境问题越来越严峻,绿色生态、可持续发展变得愈加重要,未来的研究将关注制造服务提供商的环境保护能力,将电价函数等加入优化目标,考虑结合服务提供商能耗的CMSC优化问题。