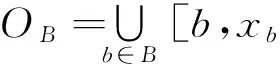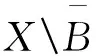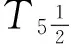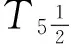关于-型邻域空间

高　瑾，罗　飞，金渝光

(重庆师范大学 数学学院，重庆 401331)



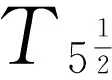
高瑾，罗飞，金渝光*

(重庆师范大学 数学学院，重庆 401331)

1　基本概念

定义3[7]设(X,V)是邻域空间，如果X的任意两个隔离子集A,B分别有开邻域U和V使得U∩V=∅,则称邻域空间是一个完全正规邻域空间.完全正规的T1-型邻域空间称为T5-型邻域空间.

定义4[7]设(X,V)是邻域空间，对任意非空闭集F,存在连续映射f:X→[0,1],使x∈F,f(x)=0和x∈Fc,f(x)≠0,则称邻域空间是一个完备正规邻域空间.完备正规的T1-型邻域空间称为T6-型邻域空间.

定义5[8]若邻域空间(X,V)是正规空间并且每一个闭子集为一个Gδ集, 则称(X,V)为完备正规邻域空间, 完备正规邻域空间的T1称为T6-型邻域空间.

关于邻域、开集、闭集的定义与文献[7]中相同,这里不一一列出.

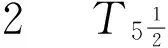
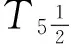
引理1[6]设X,Y是邻域空间，f:X→Y是映射，则f连续⟺邻域、开集、闭集的逆象分别是邻域、开集、闭集.

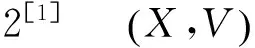
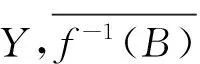
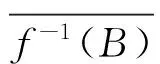
定理1完备正规的邻域空间一定是拟完备正规的邻域空间.

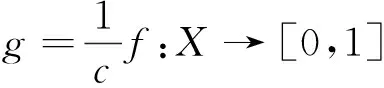
从而对任意的隔离集A,B,存在连续映射

g:X→[0,1].

使得g(x)=0,x∈A;g(x)=1,x∈B,故X是拟完备正规邻域空间.

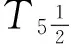
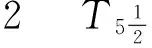
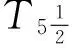
因为X拟完备正规，故存在连续映射h，令g=h∘f-1:Y→[0,1]是连续映射且

g(A)=h∘f-1(A)=0,g(B)=h∘f-1(B)=1.因此(Y,V)是拟完备正规型邻域空间.

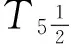
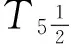
推论：

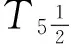
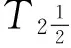
注：定理4反之是不成立的，下面将作出反例.

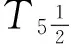
设X为一不可数集，p∈X.命X的非空开集为XC，其中C或含有点p，或为有限集.

对X任意的两点x1,x2(x1≠x2)，若该两点都不等于点p，则x1,x2任意小的邻域都是开集，并且有x1∉V(x1),x2∉V(x2).若该两点中有一点等于点p，假设点x1=p，则x1存在邻域在C里，x2存在邻域在XC里，有x1∉XC,x2∉C.故(X,V)是T1-型邻域空间.

(3)(X，V)不是T6-型邻域空间的.

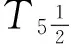
设X为实直线，令(a,b)=∪{(α,b)|a<α

(1)

则有OA是包含A的开集，类似的可以定义

(2)

由(1)(2)可以知道，对任意隔离集A和B都不存在连续映射f，使得f(A)=0,f(B)=1.故X不是拟完备正规的邻域空间.

[4]陈祥平.T3和T4—型邻域空间[J].吉林大学学报，1999,20(3):54-56

[5]陈祥平. T5和T6-型邻域空间[J]. 洛阳师范学院学报,2002(2)：11-13.

[6]熊金城.点集拓扑讲义 [M ].4版.北京:高等教育出版社,2011.

[7]朱培勇,雷银彬.拓扑学导引[M].北京:科学出版社,2009.

[8]曼克勒斯J R.拓扑学基本教程[M].北京:科学出版社,1995.

GAO Jin，LUO Fei，JIN Yuguang*

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

2016-03-17;

2016-04-20

国家自然科学基金(No.11471061)；2013年重庆高校创新团队建设计划资助项目(No.KJPB201308)

高瑾(1990- )，女，陕西礼泉，硕士研究生，研究方向：拓扑动力系统，E-mail：1015750544@qq.com

简介：金渝光( 1956- ), 男, 浙江乐清人, 教授, 硕士研究生导师，E-mail：tsgjyg@aliyun.com

O189.1

A

1671-9476(2016)05-0030-03

10.13450/j.cnki.jzknu.2016.05.007