利用同构思想巧思妙解

2024-03-07山东省枣庄市第二中学王中华正高级教师

中学生数理化(高中版.高二数学) 2024年2期

■山东省枣庄市第二中学王中华(正高级教师)

同构思想是数学基本思想之一,在数学中最简单而常用的同构类比,就是数形结合、函数与图像、代数与解析几何等。这就使得人们可以用代数方法来研究几何,或者用几何方法来解决代数问题。此思想方法常用于求解含有对数、指数等混合式子结构的等式或不等式问题。

同学们用同构法解题,除要有同构法的思想意识,还需要有较强的观察思考能力和变形转化能力。

一、在方程中的应用

选B。

感悟提升:如果方程f(a)=0和f(b)=0呈现同构特征,则a,b可视为方程f(x)=0的两个根。本题考查导数同构求解函数值,也考查运算求解能力、转化与化归思想,属于中档题。解本题的关键在于根据同构式整理得e3lnx+x-4+3lnx+x-4=elnx+lnx,进而构造函数f(x)=ex+x,研究函数的单调性,可得3lnx+x-4=lnx,即,进而求解。

二、在函数中的应用

例2已知f(x)是定义在R 上的增函数。

(2)若f(x)为奇函数,且不等式f(ax2-3x-1)+f(-ax+5)>-ax2+(3+a)x-4对任意的x∈R 恒成立,求实数a的取值范围。

(2)f(x)为奇函数,原不等式恒成立等价于f(ax2-3x-1)+ax2-3x-1>-f(-ax+5)+ax-5对任意的x∈R 恒成立,即f(ax2-3x-1)+ax2-3x-1>f(ax-5)+ax-5对任意的x∈R 恒成立。

构造函数h(x) =f(x)+x,易知h(x)是定义域在R 上的增函数。

故原不等式恒成立等价于ax2-3x-1>ax-5对任意的x∈R 恒成立,即ax2-(3+a)x+4>0对任意的x∈R 恒成立。

当a≤0时,结论显然不成立;

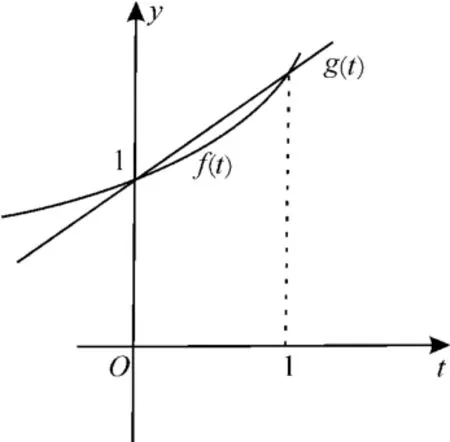
当a>0 时,则(3+a)2-16a<0,解得1

故实数a的取值范围是(1,9)。

感悟提升:对于含参的恒成立问题(不能分离型),不妨探索式子的结构特征,并将不等式左右两侧化为相同结构,合理构造新函数,利用单调性去掉“壳”,简化问题。

三、在逻辑用语中的应用

例3若a,b∈R,则“a>b”是“a|a|>b|b|”的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分又不必要条件

分析:根据不等式的结构特点构造函数,利用函数的单调性解不等式。借助不等式的性质,结合充分条件和必要条件的定义进行判断即可得到结论。

解:观察a|a|>b|b|可发现其同构的特点,依据这种结构,设函数为f(x)=x|x|,分析其单调性。

f(x)=x|x|=分析可得f(x)在定义域内为增函数。

因此,a>b⇔f(a)>f(b),即a>b⇔a|a|>b|b|,是充要条件。选C。

感悟提升:本题主要考查充分条件和必要条件的定义,可利用不等式的性质,结合分类讨论思想解题。

四、在数列中的应用

例4已知在数列{an}中,a1=5,a2=2,an=2an-1+3an-2(n≥3),求数列{an}的通项公式。

分析:可将递推公式变形为“依序同构”的特征,即关于(an,n)与(an-1,n-1)的同构式,从而将同构式设为辅助数列便于求解。

解:因为an=2an-1+3an-2,所以an+an-1=3(an-1+an-2)。

又a1+a2=7,故{an+an-1}是首项为7,公比为3的等比数列。

因此,an+an-1=7×3n-2。①

又an-3an-1=-(an-1-3an-2),a2-3a1=-13,故{an-3an-1}是首项为-13,公比为-1的等比数列。

因此,an-3an-1=(-13)·(-1)n-2。②

由①×3+②得:

4an=7×3n-1+13×(-1)n-1。

感悟提升:可以变形为an+1-x1an=x2(an-x1an-1),其中x1,x2是方程x2-px-q=0的两个根。若1是方程的根,则直接构造数列{an-an-1};若1不是方程的根,则需要构造两个数列,采取消元的方法求an。同构式在处理数列问题时,通常应用构造辅助数列求通项公式。当递推公式比较复杂时,构造出an和an-1的同构式,其中关于n的表达式f(n),f(n-1) 分别与an和an-1相对应,进而寻找辅助数列。