基于隐马尔科夫模型的滑动窗口投票策略的QRS波群形态识别

宋鑫海,韩京宇,郎 杭,毛 毅

(南京邮电大学计算机学院,江苏 南京 210023)

1 引言

据世界卫生组织统计,心脑血管疾病已成为威胁人类健康的头号杀手,预计到2030年,全球心脏病致死人数将达2 330万[1,2]。心电图ECG(ElectroCardioGraphy)作为一种无创检测手段,在临床心脏病预警和诊断中得到了广泛应用[3]。人工识别心电异常需要专业医生,存在效率低和成本高的问题,因此自动心电异常诊断受到广泛关注[4]。

在自动心电异常诊断中,主要根据心拍从前到后的不同的波形特征来识别可能的症状。一个完整的心拍从前到后依次分为P波、QRS波和T波,如图1所示。

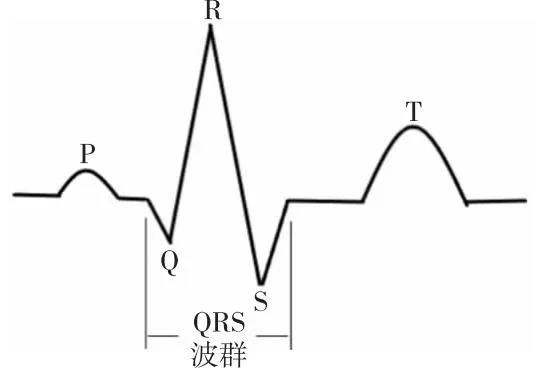
Figure 1 Waveform of a complete heart beat图1 一个完整的心拍波形

图1中QRS波群波形高大,是判断心拍的主要标志,能反映左右心室的除极状况,是诊断各种心脏疾病的重要依据。如图2所示,右束支阻滞患者通常在V1或V2导联的QRS波群表现出rSr′形态;下壁心肌梗死患者在aVR导联的QRS波群多呈rs或rS形态[5,6]。因此,QRS波群形态的准确识别是提高心电异常诊断精确度的关键。自动QRS波群形态识别面临的主要挑战有：(1)波群形态种类多达数十种,不同种类之间形态差异细小,容易误判;(2)许多波群形态的区分依赖前后相继的波形识别,为实现对不同波形的对齐,需要对波形整体进行缩放,增加了自动识别难度。

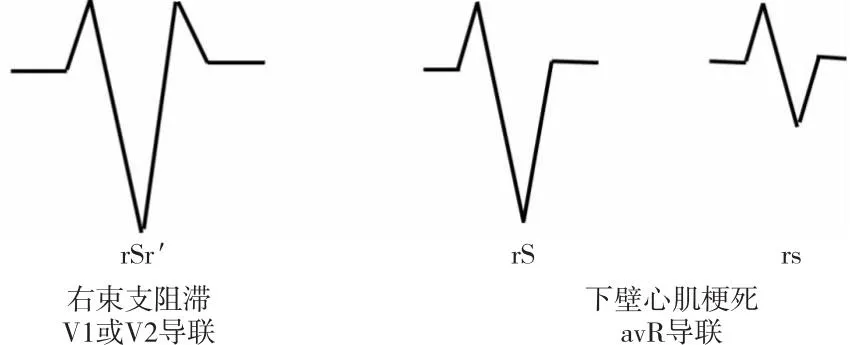
Figure 2 Different QRS waveforms of patients图2 患者不同的QRS波形示例

针对QRS形态识别,早期采用差分法、斜率判别法和小波变换[7,8]等对信号进行时频分析,以确定波峰和波谷等关键位置,完成波群形态分析。这些方法能较好地识别正常QRS形态,但对于异常或复杂波形,容易误判。后期,一些工作从ECG波形曲线拟合的角度解决问题,如采用高阶多项式曲线逼近ECG信号[9,10]、组合多种函数模拟波形[11]。这些方法简单直观,但前者参数较多,难以控制波形拟合效果,后者只能识别少数波形。

针对上述问题,本文提出一种基于状态转移受限的隐马尔科夫模型滑动窗口投票策略SWVHMM(Sliding Window Voting based on Hidden Markov Model)识别QRS波群形态。该方法对前后相继的波段窗口进行拼接,构建状态转移受限的隐马尔科夫模型来识别每个拼接的形态,进而确定最大可能的波群类型。该方法主要包含波段划分和窗口样本提取、构建状态转移受限的隐马尔科夫模型以及投票预测3个部分。首先,根据峰值和极值点提取4类前后相继的波段,并对每个波段设置滑动窗口,抽取所有窗口样本。其次,将窗口样本作为观测(Observation),波形作为状态(State),构建隐马尔科夫模型。最后,为待预测样本构建多个拼接,对所有拼接进行投票,得票最多的即为最终波群类型。

本文方法的主要优点在于：(1)每个波段取多个滑动窗口,能够捕获各波段最有效的局部观测。(2)隐马尔科夫模型可以充分体现波段前后相继的依赖关系,根据波群的整体特征来识别波形,不会囿于局部波段来判断整体。(3)通过对波段的序列进行拼接,产生多个样本代表,进而通过投票进行判断,保证了方法的泛化性和鲁棒性。

2 相关工作

2.1 去噪方法

常用心电信号去噪方法有数字滤波器、基于小波变换的阈值去噪、数学形态学法(Mathematical Morphology)和经验模态分解EMD(Empirical Mode Decomposition)。

数字滤波器针对不同噪声频率,选择合适的高通或低通滤波器去噪,实时处理,但滤波后T波容易被误判为R波[12];小波变换对信号进行时频分析,通过伸缩平移对信号多尺度细化,实践证明对非平稳信号效果较好[8];数学形态学法以积分几何和代数等数学理论为基础,使用被称为“探针”的结构元素来最大程度地保留信号形态特征,较好地保证了ECG完整性,但是去除低频噪声效果不佳[13];EMD将信号分解为多个本征模态函数IMF(Intrinsic Mode Function),再通过组合IMF达到去噪目的[14]。此外,还有许多组合改进算法,例如文献[15]将EMD与小波变换相结合,取得了较好的去噪效果。

2.2 QRS波形识别

传统检测QRS波群主要有阈值检测和模板匹配等方法。阈值检测因为占用内存小、运行速度快,被广泛用于可穿戴式心电设备,但该方法对信号质量要求高,容易受噪声干扰,准确率有待提高[16]。模板匹配直观简单,但检测速度慢,且严重依赖模板[17]。此外,还有多种新方法用于QRS检测,例如文献[18]结合小波变换和希尔伯特变换检测含噪声的心电信号;文献[19]提出了基于一维卷积神经网络1D CNN(one Dimensional Convolutional Neural Network)的QRS检测算法。这些方法对于正常波形能取得较好检测效果,但对于异常或不规则波形的检测效果不佳。

针对传统检测方法的不足,面对QRS复杂形态,还有研究从拟合曲线角度进行检测。毛玲等[10]提出了一种QRS波群关键点结合有限状态机的形态分析算法FSM-QRS(Finite State Machine for QRS complex),采用二次多项式曲线分段逼近心电信号;然后分析各段曲线的陡峭性和单调程度等特征,以此检测并分析波峰和波谷等关键点;最后,构建有限自动机,输入关键点序列,实现QRS形态识别。上述算法能够识别多种波形,但需要设定多种参数,如预定角度和阈值等,效果难以控制。Caldas等[11]提出基于数学函数组合建模残差RCMF(Residual modeling with Composition of Mathematical Functions)的特征提取方法,利用Gaussian、Rayleigh和Mexican Hat函数构建数学模型拟合波群形态,对所选函数进行标准化使其峰值相等,便于合并函数,然后将所得模型与输入QRS波群形态进行对比,计算二者的均方误差,将均方误差最小值所对应的模型作为波形分类的最终模型。上述方法仅能够识别少数波形,且时间复杂度较高。

3 方法概述

3.1 方法概述和相关概念

本文方法主要包含3个阶段,即波段识别和窗口样本提取、构建状态转移受限的隐马尔科夫模型和多窗口样本投票,本文方法框架如图3 所示。第1阶段,在清除切迹后,根据极值点和R波识别4个波段,各波段利用滑动窗口提取多个窗口样本;第2阶段,对各波段窗口样本聚类以构建状态转移受限的隐马尔科夫模型;第3阶段,针对待预测波群,利用滑动窗口获得多个候选样本,每个候选样本通过模型得到预测波形,最后投票所有波形,输出最终结果。

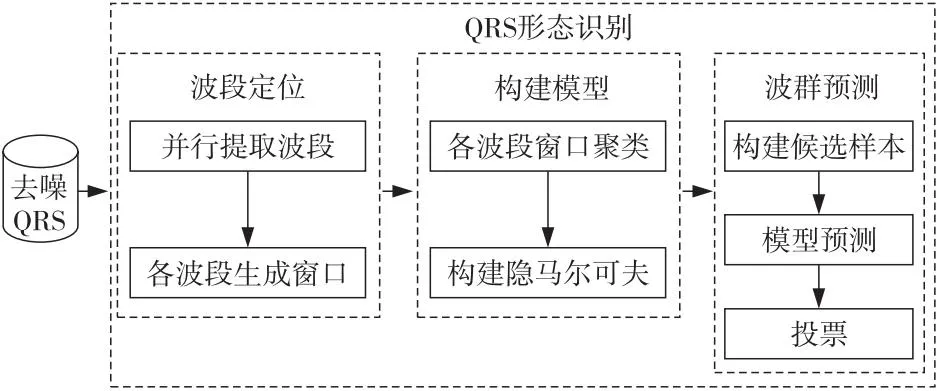
Figure 3 Framework of the proposed method图3 本文方法框架

一个QRS波群是一个心拍中的连续点序列〈(X1,Y1),…,(Xi,Yi),…,(Xn,Yn)〉,其中Yi(1≤i≤n)表示Xi时刻的电压。一个QRS波群中的波段定义如下：

定义1(波段) 一个QRS波群从前到后分为Q、R、S和R′ 4段。各波段呈现不同波形,记为{Q,q,Nq},{R,r,Nr},{S,s,Ns},{R′,r′,Nr′}。其中Nq、Nr、Ns和Nr′表示对应波段不存在相应波形。

在QRS波群中,每个波段的波形根据形态、方向、幅度及前后相继关系来判定,如图4所示。第1个向下波属于Q波段,振幅大于0.5 mV的记为Q波,小于0.5 mV的记为q波,表现为平直线段的记为Nq;第1个向上波属于R波段,第2个向下波属于S波段,在S波段后出现的第1个正向波属于R′波段,各波段波形描述和Q波段相同。当心脏传导系统异常,QRS波群还会出现切迹和顿挫现象。其中,切迹指QRS波群中各波的上升或下降部分有方向和斜率发生改变的节段;顿挫指QRS波群中各波的上升或下降部分有斜率发生改变,而方向不变的节段[10]。根据欧洲定量心电图通用标准CSE(European project entitled Common Standards in quantitative Electrocardiography)[20]规定,若切迹等各种波形存在,必须满足时间不少于6 ms,振幅不小于0.1 mV 2个条件。

Figure 4 Typical QRS shape图4 典型QRS形态

3.2 波形去噪

心电信号受基线漂移、工频干扰和肌电干扰等噪声影响[3],波形识别前要先滤波去噪,使信号平滑。使用小波变换去除工频干扰和肌电干扰[8]：采用bior4.4小波基,根据噪声频率分布对小波8阶分解后的低频和高频分量进行软阈值去噪,最后小波重构得到连续信号。之后对该连续信号使用6阶Butterworth 滤波器,其截止频率为0.5 Hz,去除基线[21]。

之后采用经典的Pan-Tompkins双阈值算法[22]进行R波定位。通常QRS波群时长不超过0.2 s,故以R波为中心,前后各取0.1 s作为形态检测区域。整个去噪前后对比如图5所示。

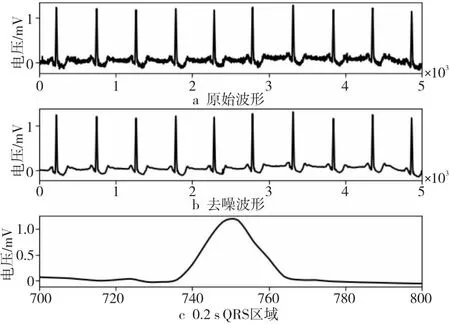
Figure 5 Waveforms comparison before and after denoising图5 去噪前后波形对比

3.3 各波段定位和窗口样本提取

QRS波群形态复杂多变,各波段检测会受到切迹的干扰。如图6所示,在R波下降部分出现方向向上的曲线ABC,会让极小值点A识别为S波段,导致波形误判。因此,在利用极值点定位波段前要先排除切迹干扰。

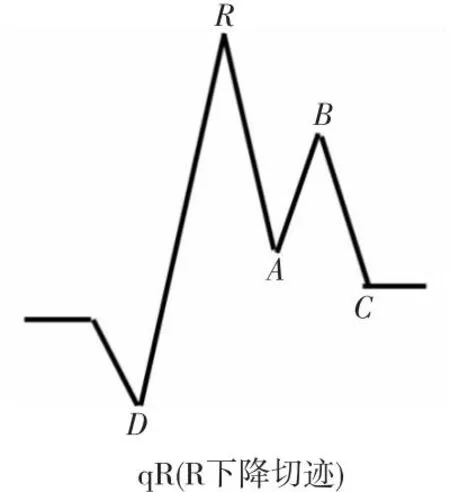
Figure 6 qR wave with notch图6 伴随切迹的qR波形

(1)

(2)

其中,sample指采样率。

搜索波群内所有极值点,在排除切迹后,检测剩余极值点位置来判断波段类型。如图6的Q波段,在峰值R左侧存在首个极小值点D,取D前后一段时间作为Q波段[6]。关于波段长度,文献[6]指出正常Q波段存在0.04 s,不同波段存在时间不同。

定义2(权重窗口样本) 每个波段对应一个区域〈(X1,Y1),…,(Xn,Yn)〉,给定滑动窗口长度m,可以获取n-m+1个窗口样本,第i个窗口对应的子序列是〈(Xi,Yi),…,(Xi+m,Yi+m)〉。

本文根据每个样本相对波段中心的位置来确定其权重,因为越靠近波段中心的样本,形状特征越强,越能够有效识别波段形态。记波段区域长度Lc=Xn-X1,中心位置Cc=X1+Lc/2;第i个窗口中心位置Dc=Xi+(Xi+m-Xi)/2,其权重如式(3)所示：

(3)

样本距离波段中心越近,权重越大,当距离为0时,权重为1。所有样本权重在[0,1]变换,便于计算。

4 构建状态转移受限的隐马尔科夫模型

4.1 波形聚类构建观测代表

由于每个波段的滑动窗口会取得多个窗口样本,所有实例对应的窗口样本数目会非常庞大,不便于直接采用隐马尔科夫建模。为此,提出通过聚类识别窗口样本的类簇,用每个类簇表示一类窗口样本,从而用有限个类簇中心来表征可能的观测。

常见的聚类方法有：基于距离的划分聚类方式,代表算法为K-means(K-means clustering algorithm),要求随机选取k个对象作为聚类中心,之后计算每个对象和聚类中心的距离[23];基于密度的聚类方式,如DBSCAN(Density Based Spatial Clustering of Applications with Noise),其任意选择一个核心点,然后寻找所有从该点密度可达的样本,形成类簇[23];基于图论的聚类方式,如谱聚类,利用无向带权图表示数据集中对象,之后根据相关准则划分该无向图,将聚类转换为图的构建与切分问题[24]。其中,K-means适用于发现特定形状的数据集,而DBSCAN和谱聚类可以发现任意类型的数据。相比于谱聚类,DBSCAN还具有较强的抗噪性,更符合心电信号微弱、易受噪声影响的特点。同时,由于时间序列的滞后性,如欧氏距离、曼哈顿距离等不足以描述序列相似性,为更好地度量窗口样本的相似性,使用规范化后的互相关系数作为距离度量[25]。

给定2个长度为m的窗口样本S和T,为搜索二者在形态上的相似性,固定T,令S左右滑动产生相位偏移,如式(4)所示计算每次偏移后二者内积Rt：

(4)

整个滑动过程共产生2m-1个内积,如式(5)所示：

C(S,T)=max(Rt)=max(Rw-m),

w=1,2,…,2m-1

(5)

其中,t<0表示S向左滑动|t|个单位长度,最大值即为最佳相位匹配,然后如式(6)进行归一化。互相关系数Nor越大,说明样本相似性越强。

(6)

传统DBSCAN聚类要求设置密度半径等参数,若参数设置不当,则会影响聚类效果[26]。本文提出基于样本稀疏程度来进行DBSCAN聚类,使用样本平均密度和标准差描述样本稠密性,具体步骤如下所示：

(1)离群点判断。每个样本,包括随机初始样本在拓展形成小类簇前,都要判断是否为离群点,如果是离群点就忽略该点,其判断依据为样本的稠密程度,定义如下所示：

定义3(窗口样本密度) 给定窗口样本xi,其密度Dxi形式化如式(7)所示：

(7)

其中,N是以xi为圆心、Rxi为密度半径的圆内样本个数。

定义4(平均密度) 给定窗口样本xi,平均密度是其密度半径内所有样本的平均密度,如式(8)所示：

(8)

定义5(密度标准差) 给定窗口样本xi,密度标准差用来衡量其密度半径内样本的离散程度,如式(9)所示：

(9)

(3)将类簇C内每个样本作为新的簇心向外拓展,重复步骤(2)形成多个类簇,直到不能发现新的小类簇。之后合并这些小类簇组成最终大类簇Z。对于剩余样本,重复步骤(2)和步骤(3)不断形成新的大类簇,直至所有样本聚类完成。

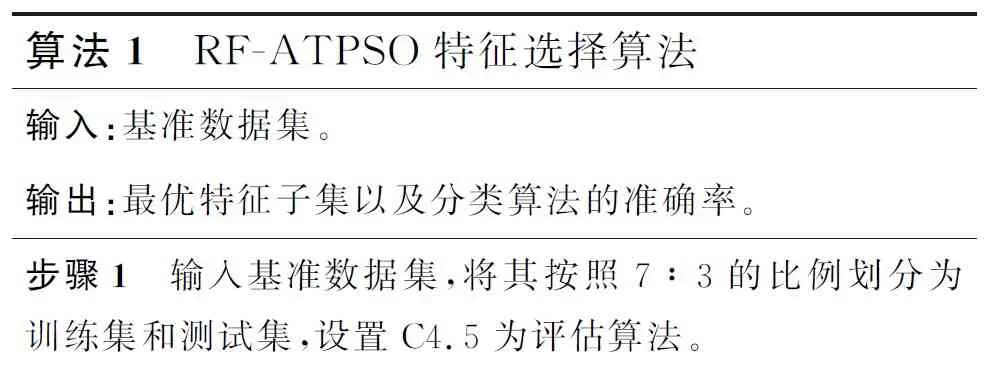
算法1 波形聚类输入：波段窗口样本集合Ls;簇内样本个数k。输出：观测集合Observation。1：Z←⌀;2：while L.size>0：3： /∗随机选择样本P,根据式(7)～式(9)判断是否为离群点∗/4： if P is not noise：5： search k samples which are close to P;6： calculate k samples′ mean as R;7： //得到以P为圆心、R为半径的小类簇C8： Z.add(C);9： for each Ci in C：10： repeat step 6 and step 7 to get clusters Bi;11： Z.add(Bi);12： end for13： calculate the cluster center Tc for Z;14： Observation.add(Tc);15： Ls.remove(Z);16： else：17： Ls.remove(P);18： end if 19：end while 20：return Observation;

算法的时间复杂度为O(n*m2),其中n为波段窗口样本个数,m为窗口样本的长度。

4.2 构建状态转移受限的隐马尔科夫

本文方法所构建的隐马尔科夫模型状态的转移是受限的,只能从当前波段状态转移到后继波段状态,如从Q波段转移至R波段,从R波段转移至S波段等。一个转移受限的隐马尔科夫模型可表示为五元组HMM=(H,S,O,TR,EM)。其中,H表示初始状态(Q,q,Nq);S代表所有状态,包括Q,q,Nq,R等;O代表观测,即聚类获得的类簇中心;TR是状态转移概率;EM代表发射概率,即在每个状态下能够看到观测的概率。假设存在波群qRs和qrs各200个,qRS和qrS各100个,其状态转移概率如图7所示。

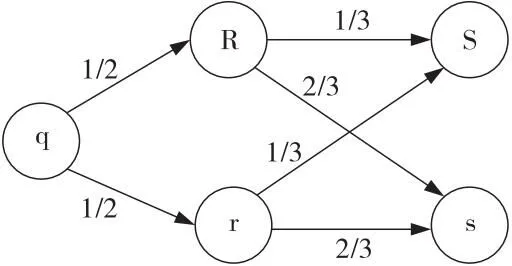
Figure 7 Illustration of state transition probability图7 状态转移概率示意图

采用监督学习方法构建隐马尔科夫模型：在所有训练样本上统计各个观测值,就可以构建对应的隐马尔科夫模型。其中,初始状态分布H可由训练集样本中Q波段出现频率估计;状态转移概率TRu,v和发射概率EMv,o可形式化为式(10)和式(11)所示：

(10)

(11)

其中,Au,v表示当前时刻状态u在下一时刻转移到状态v的出现频数;Bv,o表示状态v时观测为o的出现频数。

5 基于多窗口波群形态预测

采用候选样本投票方法来决定最终的波群形态。首先,构建样本代表,然后对每个样本代表计算预测波群类型,最后多个波群投票,具体步骤如下所示：

(1)构建候选样本。

定义7(候选样本) 给定一个QRS波群,设其Q波段对应X个观测样本,分别记为{Q1,…,Qi,…,QX};R波段对应Y个观测样本,记为{R1,…,Rj,…,RY};S波段对应ZS个观测样本,记为{S1,…,Sm,…,SZS};R′波段对应W个观测样本,记为{R′1,…,R′n,…,R′W}。则一个候选样本是4段的拼接,记为O=(Qi,Rj,Sm,R′n),即一个待预测QRS波群会产生X*Y*ZS*W个候选样本。

(2)模型预测。

对每个候选样本,应用隐马尔科夫模型获取其对应的波群形态,即在已知模型HMM和观测序列O情况下,求解最大可能波群形态T,可形式化为式(12)所示：

(12)

P(O|HMM)为常数,问题转化为求解maxP(T,O|HMM)。利用Viterbi算法求解该最优化问题,定义μtb(u)为波段tb(tb∈{Q,R,S,R′})时,终止状态为u的所有路径中最大概率,则波段tb+1最大概率表示如式(13)所示：

μtb+1(u)=max(EMu,Otb+1·μtb(v)·TRv,u)

(13)

求解到R′波段预测状态后,向前回溯求解波群类型T。

(3)投票。

算法2 QRS波群形态预测输入：待预测波群Wy;隐马尔科夫模型HMM。输出：最大概率波群类型。1：dict←⌀; // key为预测波形,value为概率2：generate all candidate samples S for Wy;3：for each s in S：// 各候选样本s4： calculate weight probabilities P for s;5： predict the waveform T according to the Viterbi algo-rithm;6： if T in dict：7： dict[T]←dict[T]+P;8： else：9： dict[T]←P;10： end if11：end for12：sort dict in descending order by value;13：return dict.keys()[0];

时间复杂度为O(q*m),其中O(m)为单次运行维特比算法的时间复杂度,q为候选样本个数。

6 实验与结果分析

6.1 实验设置

为检验本文方法性能,采用12导联心电数据DS-COM[27]进行测试。该数据集共包含6 000个样本,采样率为500 Hz,时长为10 s。为测试结果正确与否,请心电专家对QRS波群进行人工识别。实验共抽取11种形态的QRS波群,分别为：RS波350个,qRs波300个,qRsr′和rSr′波各200个,Qr、QS、R和rS波各150个,qR,Rs和qrs波各100个,总计1 950个。

本文实验采取6轮交叉验证,即将数据集均分为6份,依次分6轮进行模型构建和测试,最后取平均实验结果。每轮中,5份数据用于构建马尔科夫模型,另外1份用做测试集。为验证本文方法的有效性,采用精确度PR(PRecision)、召回率RL(RecaLl)和FS(F1-Score)度量指标,其定义分别如式(14)～式(16)所示：

(14)

(15)

(16)

其中,TP表示正样本被模型预测为正类的个数,FP表示负样本被预测为正类的个数,FN表示正样本被预测为负类的个数。

6.2 方法性能评估

(1)簇内样本个数k对波段聚类效果的影响。

使用轮廓系数表征k对各波段聚类效果。图8展示了k对Q波段聚类的影响,随着k增大,轮廓系数先上升后下降,并且幅度较大,说明聚类对k较敏感。

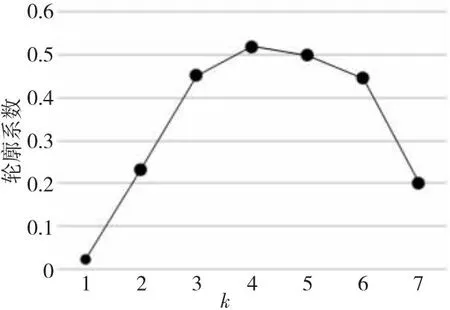
Figure 8 Effect of k on the clustering silhouette coefficient图8 k对聚类轮廓系数的影响

(2)滑动窗口尺寸效果分析。

本文方法通过滑动窗口提取各波段样本,其窗口尺度会影响最终预测效果。图9展示了窗口尺度对11种波形平均预测结果的影响。当窗口尺度在[4,6]时,波形识别性能没有较大波动;但当窗口过大或过小时波形预测效果不佳。

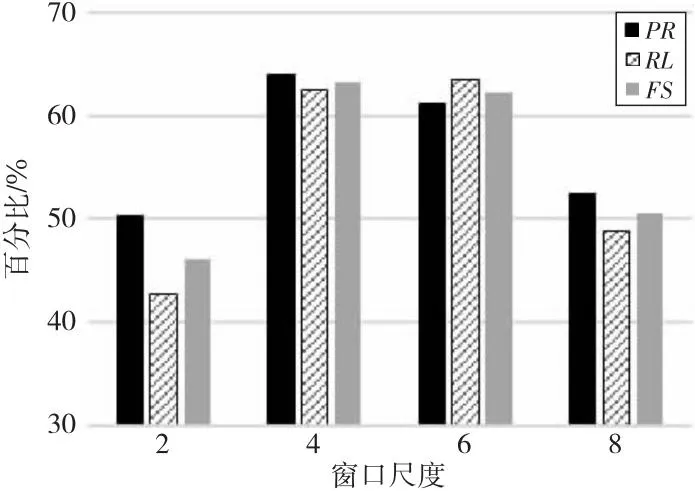
Figure 9 Effect of window size on waveform prediction图9 窗口尺度对波形预测的影响

(3)聚类算法的比较。

对于K-means,利用手肘法找出最佳k值并聚类[23];对于谱聚类,采用KNN(K-Nearest Neighbor)算法遍历所有样本构建无向图,并使用NCut(Normalized Cut)方式切图聚类[24]。使用轮廓系数来表征3种算法对Q波段聚类的效果。如表1所示,K-means效果最差,其轮廓系数为0.389 5;谱聚类次之,轮廓系数为0.501 4;本文算法最佳,轮廓系数为0.520 7。这是因为相比于K-means,谱聚类和DBSCAN对数据集不敏感,同时DBSCAN抗噪声能力更强。

Table 1 Results comparison of clustering algorithms

6.3 对比实验

与FSM-QRS[10]、RCMF[11]和1DLBPAT(1-Dimension Local Binary Pattern with Adaptive Threshold)[28]3种方法在DS-COM数据集上进行对比测试,相关参数与实验结果如下所示：

(1)FSM-QRS：连续拟合点的个数k=5,误差阈值ε=0.01,预定阈值thr=0.004,方向角度α=0.03,β=0.02。

(2)RCMF：Rayleigh和Mexican Hat函数的参数λ∈{0.1,0.5,…,10};Gaussian函数的参数μ=0,σ2∈{0.1,0.5,…,10}。

(3)SWVHMM：簇内样本个数k为4,窗口尺度为5。

(4)1DLBPAT：对经过EMD分解后的IMF使用LBPAT算法检测R波,其阈值AT由截止频率为3 Hz的低通滤波器滤波后的信号和该信号的平均值线性叠加构成。

如图10～图14所示,对比FSM-QRS,SWVHMM在RS波形上,PR、RL和FS分别提升了11.07%,6.37%和8.54%;在qRs波形上,PR、RL和FS各自提升了9.50%,2.60%和5.72%;Qr波形的PR、RL和FS分别提升了4.89%,4.67%和4.78%;8种波形PR、RL和FS平均提升了6.46%,3.42%和4.85%。

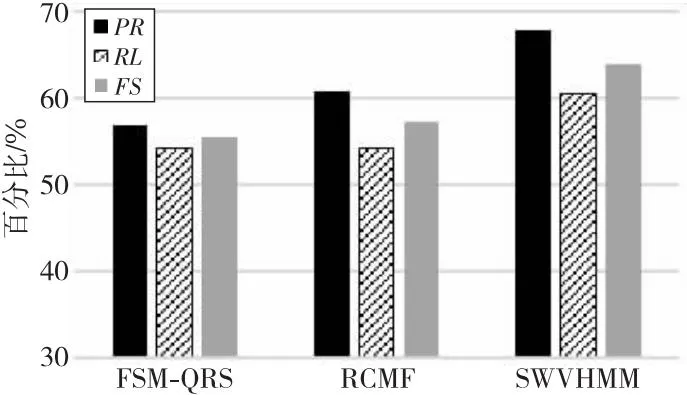
Figure 10 Experimental results of RS waveform comparison图10 RS波形对比实验结果

相比RCMF,SWVHMM在RS波形上,PR、RL和FS分别提升了7.13%,6.28%和6.68%;在qRs波形上,PR、RL和FS各自提升7.00%,6.81%和6.94%;Qr波形的RL下降了1.96%,PR和FS上升了7.52%和2.86%。对比1DLBPAT,SWVHMM在R波形上,PR、RL和FS分别提升了1.33%,3.19%和2.27%。

结果表明,相比于FSM-QRS、RCMF和1DLBPAT,SWVHMM使得指标FS的平均值提高了5.97%,5.49%和2.27%。该方法能够取得更好效果的原因在于：相比于RCMF和1DLBPAT,SWVHMM利用滑动窗口提取波段局部特征,再利用隐马尔科夫模型描述波段前后相继的整体关系,从而能够识别更多形态;相比FSM-QRS控制参数较少,降低了参数敏感性。

7 结束语

QRS波群形态是许多心脏疾病诊断的主要依据。早期的差分法和斜率判别法等只能处理简单形态;后期从波形曲线入手,利用各种函数拟合心电信号,但存在只能识别少数波形或参数过多、难以控制的缺点。本文提出基于隐马尔科夫的滑动窗口投票策略,包含波段划分及窗口样本的提取、构建状态转移受限的隐马尔科夫模型和多窗口预测3个部分,可识别出多种QRS波群形态,并且准确率更高、鲁棒性更好。后续将考虑如何更好地描述窗口样本相似性和序列聚类,以及如何更好地定位R波。