基于本质安全的新型乙炔溶解度测量方法

2024-02-02穆垚，程易

天然气化工—C1化学与化工 2024年1期

穆垚，程易

（清华大学化学工程系，北京 100084）

作为最基本的化工原料之一，乙炔从20世纪早期就被用于合成多种大宗化学品和精细化学品[1]，目前，中国已经成为全球最大的乙炔生产国之一。乙炔在精细化工领域应用广泛，可用于合成一系列高值化学品，如1,4-丁二醇、各类N-乙烯基化合物（如N-乙烯基吡咯烷酮、N-乙烯基咔唑）等[2-3]。其中，N-乙烯基化合物是一类高价值化合物，在医药、电子化学品等领域有着广泛应用[4-5]，其一般合成方法为乙炔直接加成引入乙烯基（即乙炔法）[6]，该方法具有路径短、工艺成熟及成本低等优点，是目前最具工业可行性的方法。但是，由于乙炔在加压条件下易发生分解爆炸[7]，通常只能在常压下混合惰性气体使用，导致液相中乙炔溶解度很低，反应过程的效率受限。为解决此问题，一种思路是采用对液相加高压的方法[8]，先将乙炔溶解于溶剂，再将溶液进一步在高压和高温条件下反应，反应过程中需要足够压力保证无乙炔析出，避免气相乙炔的存在，降低乙炔的爆炸风险，同时液相中乙炔浓度高，可提高反应效率。为科学地设计反应工艺，溶剂筛选和反应压力的确定至关重要，因此获取乙炔在不同溶剂中、宽温度压力范围内的溶解度数据十分关键。

然而，目前文献中报道的乙炔溶解度数据并不丰富，多为在常见溶剂中，低温、低压（50 °C、0.2 MPa）条件下的乙炔溶解度数据[9-15]，因此研究者们在设计乙炔相关反应时，通常需要根据实际体系，通过实验测得乙炔溶解度。常见的气体溶解度测量方法包括静态饱和法、恒定容积法、泡点压力法、平衡液体取样法和天平称重法等[16]。总的来说，以上方法都需要先构建封闭的气液平衡体系，再通过测量体系中的物理量变化或者取样来进行溶解度的测量。构建气液平衡体系时，常用的容器是搅拌釜，为保证气液达到传质平衡，通常需要连续搅拌24 h[17]，效率较低，更重要的是，加压、高温下乙炔的易爆性导致溶解度测量存在较大的安全隐患。

微化工设备具有比表面积大、传质效率高和温度均一等优点，在处理危险过程时，由于空间受限以及原料用量少，相比传统化工设备有更好的安全性[18]。此外，乙炔/氮气混合气的爆炸实验还表明，爆炸的临界压力与容器体积有关，容器体积越小，乙炔爆炸的临界压力越高，安全性越好[7]。因此采用微化工设备进行乙炔溶解度的测量，可以降低乙炔爆炸的可能性和危害性，从本质上提高乙炔溶解度测量实验的安全性。

本研究使用内径为0.8 mm 的石英管，基于静态饱和法的基本溶解度测量原理，设计和构建具有本质安全性的乙炔溶解度测量微化工设备，通过理论计算和实验测定装置所需气液平衡时间，以期实现以乙炔为代表的危险气体在高温高压下的溶解度安全测量。

1 实验部分

1.1 实验试剂

实验所用试剂见表1。

表1 实验所用试剂Table 1 Experimental reagents

1.2 实验装置与方法

本研究构建的溶解度测量装置使用可视效果好、耐温耐压性好的石英管作为溶解度测量容器，使用液态金属作为液封剂，将乙炔和溶剂封闭在石英管内，基于静态饱和法进行溶解度测量。石英管内径仅为0.8 mm，最多可装入约7 μmol乙炔。按乙炔的标准燃烧焓（-1299.63 kJ/mol）计算，装入的乙炔完全燃烧放热仅约9 J，因此测量过程具有本质安全性。所用液态金属的化学本质为镓铟锡合金，熔点为16 °C，沸点在2000 °C 以上，在实验过程中保持液态，与溶剂无反应。

石英管封装示意图见图1，先通过微量进样针装入约10 μL 溶剂并将其离心至石英管底部，随后通过质量流量计控制气速的毛细不锈钢进气管通入乙炔直至液柱到达石英管口。通气完成后，迅速将石英管插入不锈钢耐压瓶中，通过瓶盖上的卡套将其与耐压瓶固定，由于耐压瓶内装有液态金属，可以对石英管内的气液体系形成液封，该装置的实物和示意图见图2。随后，通过氮气对耐压瓶加压，压力通过液态金属传导，使气液封闭体系压力升高。加压完成后，关闭与耐压瓶相连的截止阀并将装置取下静置，方便多组平行实验同时进行。在静置足够时间（约1.5 h）后，气液体系达到静态饱和状态，此时石英管内的气柱长度不再发生变化，读取并记录气柱、液柱高度和压力传感器显示的最终压力，经过数据处理后计算得到乙炔溶解度。

图1 石英管封装示意图Fig. 1 Schematic diagram of quartz tube packaging

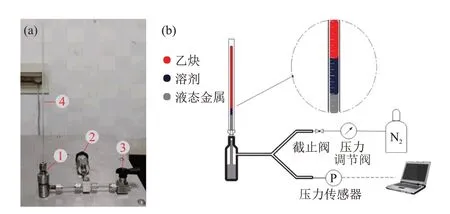
图2 装置实物(a)和装置示意图(b)Fig. 2 Physical device (a) and schematic diagram of device (b)

1.3 实验数据处理方法

根据液体压强公式，可以通过测得的表压计算气柱压力，见式(1)。

式中，pg、p表、pl、p金和p0分别表示气柱压力、测得的表压、溶剂液柱压力、液态金属液柱压力和标准大气压，Pa；ρl、ρ金分别表示溶剂、液态金属的密度，kg/m3；hl、h金分别表示溶剂、液态金属的液柱高度，m；g为重力加速度，m/s2。

利用理想气体状态方程，可以计算气柱中的气体量，见式(2)。

式中，n余为气柱中的气体量，mol；hg为气柱长度，m；d为石英管内径，m；T为实验温度，K；R为气体常数，8.314 J/(mol·K)。

理论上，气柱中的气体量和溶解的气体量之和为常数，而根据亨利定律，气体溶解量和气柱压力成正比关系。因此，以一组实验数据为例（表2），证实了剩余气体量在20%以上时与气柱压力有较好的线性关系，见图3(a)。

图3 剩余气体量与气柱压力的关系(a)和不溶性气体矫正后剩余气体量与乙炔分压的关系(b)Fig. 3 Relationships between amount of residual gas and gas column pressure (a) and relationships between amount of residual gas after correction of insoluble gas and partial pressure of acetylene (b)

表2 实验数据样例Table 2 Samples of experimental data

然而，由于乙炔气中混有的微量不溶性气体（如氮气），随剩余气体量的减小，气柱压力和剩余气体量的关系偏离线性。为了对不溶性气体的影响进行校正，通过乙炔分压与气柱总压力之间的关系、质量守恒关系和亨利定律的变形形式，分别见式(3)～式(5)，得到气柱压力与剩余气体量的函数关系，见式(6)。

式中，pC2H2为乙炔分压，Pa；nN2、nC2H2、n溶和n总分别为氮气量、乙炔量、溶解在液相的气体量和乙炔与不溶性气体量之和，mol；k为与温度、溶剂有关的常数，Pa/mol。

根据式(6)，将nN2作为参数，使用MATLAB对实验数据进行拟合，得到不溶性气体量。以表2 的数据为例，计算得到不溶性气体量为0.0642 μmol，仅占通入气体总量（6.8 μmol）的0.9%，说明石英管封装过程仅混入了少量的不溶性气体。排除不溶性气体的影响后，可以得到乙炔分压与剩余气体量之间的关系，即二者线性关系较好（图3(b)）。如果拟合计算得到的不溶性气体含量较多（超过5.0%），则说明封装过程中混入的不溶性气体较多，应该重新进行封装，否则会限制设备可实现的最大乙炔分压。由于气液平衡体系被液态金属完全封闭，对于一台仪器，仅需要根据低压的实验数据进行一次校正以获取不溶性气体的量。确定nN2后，在后续的实验过程中可以根据气柱长度、压力表压力快速计算得到乙炔溶解量。最后，根据液柱高度，可以计算得到溶剂物质的量，计算方法见式(7)，进而可以通过计算得到乙炔溶解度（式(8)）。

式中，n1为溶剂物质的量，mol；Ml为溶剂的摩尔质量，kg/mol；x为乙炔溶解度。

2 结果与讨论

2.1 气液平衡时间分析

2.1.1 气液平衡时间理论计算分析

实验中，需要在加压后静置等待体系达到气液平衡，确定所需平衡时间，以保证测量准确性并提高实验效率。本节通过理论模型计算对本装置的气液平衡时间进行了估算。

在加压完成后，虽然因为气体的溶解，体系的压力会略有减小，但变化幅度不大，故这个过程可以近似为恒压气体向半无限大液体传质的一维传质过程。前期实验已经发现了不同长度的液柱的气柱稳定时间有较大差别，说明该过程主要的传质阻力在于液柱内的分子扩散，故忽略气相和气液界面的传质阻力，建立液相中的分子扩散模型。此过程的传质微分方程见式(9)，边界条件见式(10)和式(11)，微分方程的解见式(12)。

式中，CA为乙炔浓度，mol/m3；t为传质时间，s；y为传质深度，m；D为分子扩散系数，m2/s；CAw为平衡时的乙炔浓度，mol/m3；erf(N)为误差函数，变量

当erf(N)=0.99959 时，可认为此时液柱内浓度达到传质平衡状态，此时N=2.5。液相中的分子扩散系数的量级为10-9m2/s，故按D=1×10-9m2/s进行估算，可以得到液柱高度与理论传质平衡所需时间的关系（表3）。由表3可知，对于6 mm高度液柱，通过分子扩散，在约24 min内就可以达到传质平衡。

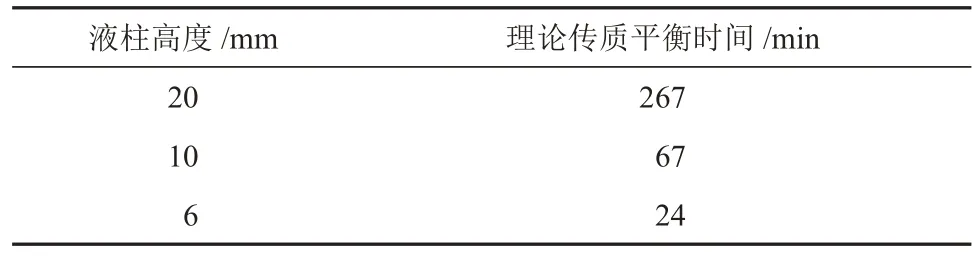
表3 液柱高度与理论传质平衡时间的关系Table 3 Relationships between liquid column height and theoretical mass transfer equilibrium time

2.1.2 气液平衡时间实验测定分析

本节通过实验测定了本装置达到气液平衡所需时间。在充压后，由于气体的溶解，体系中的压力会略微降低，通过测定该压力衰减的过程，可以判断溶解是否已经达到平衡，从而确定设备所需的传质时间。在测试实验中（溶剂：四氢呋喃，温度：25 °C，液柱高度：6 mm），石英管充压后的压力随时间的变化曲线见图4。由图4可知，约1500 s后压力不再发生变化，仅由于温度波动等原因出现微小的压力波动，说明体系已经达到了气液传质平衡，与理论计算的气液平衡时间基本一致。

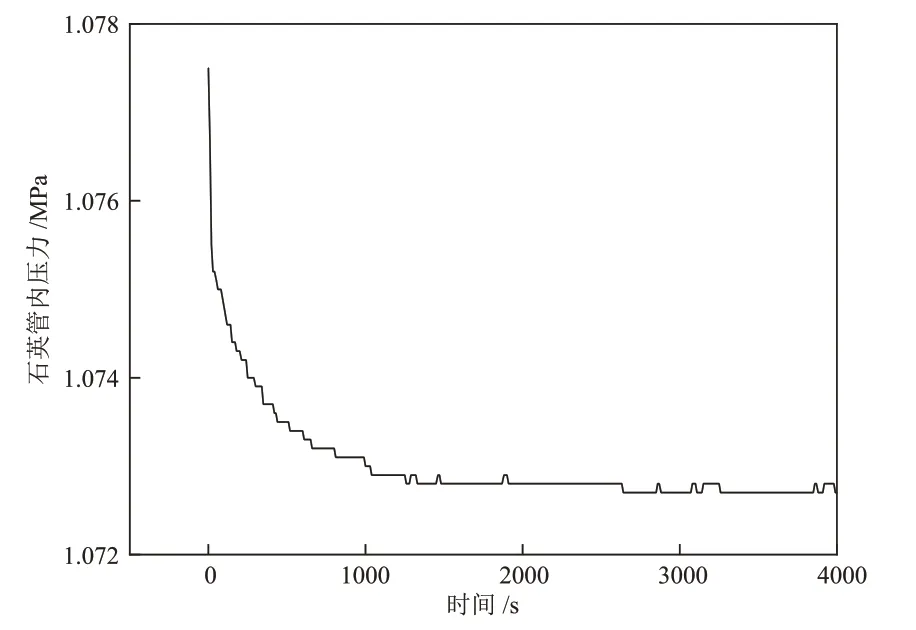
图4 石英管内压力随时间的变化Fig. 4 Changes of pressure in quartz tube with time

溶解度测量过程中所使用的石英管内液柱高度为6～10 mm，通过理论分析计算和实验方法确定所需要的平衡时间为1～2 h。由于微化工设备传质快的特点，即使在封闭的气液体系内没有采用搅拌等方式强化传质，其所需的气液传质时间也较常规搅拌釜（24 h）更短。因此，采用此方法的乙炔溶解度测量效率更高。

2.2 溶解度测量数据分析

采用设计的乙炔溶解度的测量方法，测量了乙炔在不同温度和压力下时，分别在2-吡咯烷酮、N-甲基吡咯烷酮、丙酮、甲醇、四氢呋喃和正丁醇6 种溶剂中的溶解度，并和文献[3,9]中的数据进行了对照，结果见图5，测得的乙炔在不同溶剂中的溶解度基本符合亨利定律。

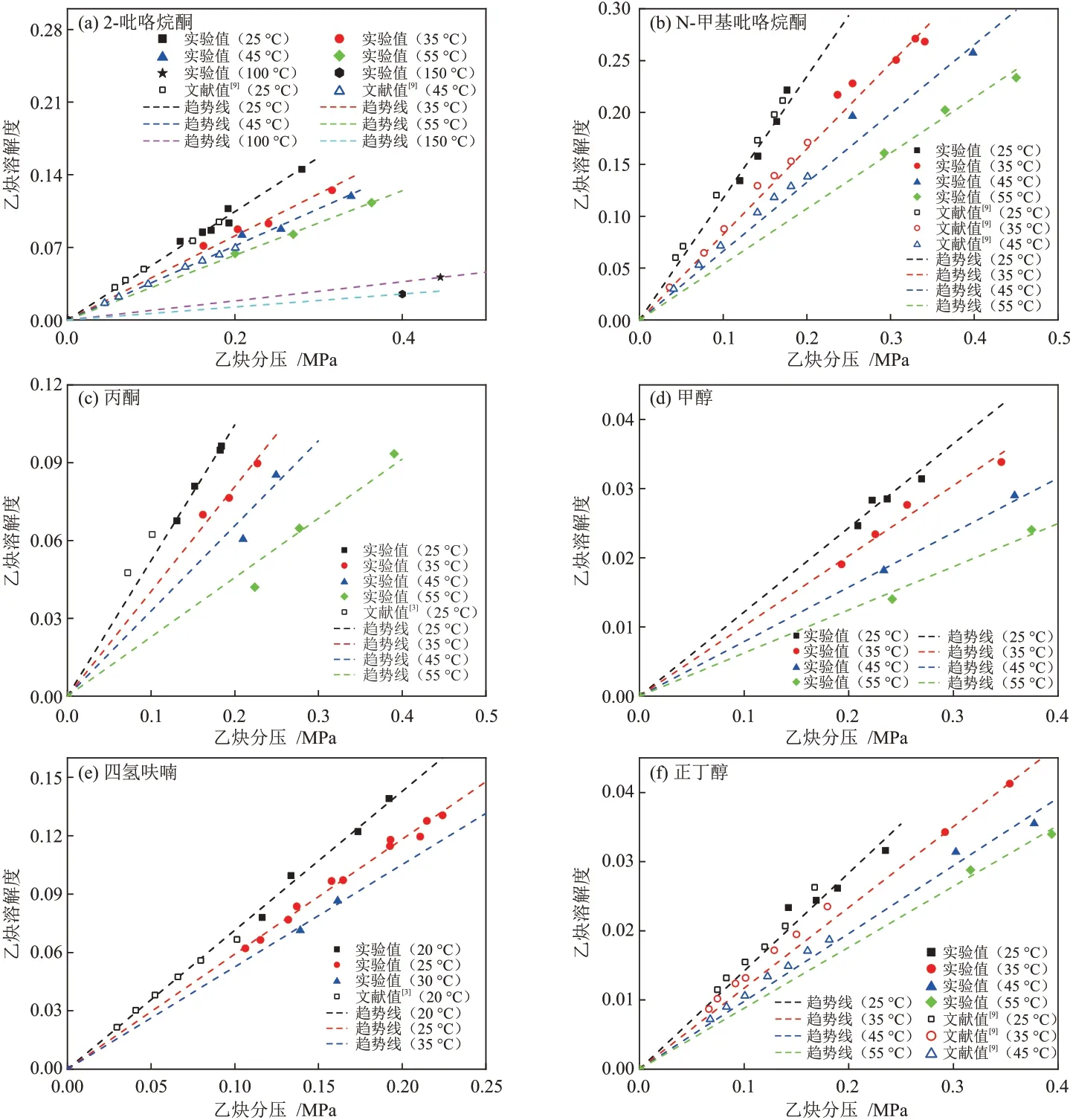
图5 乙炔在不同溶剂中的溶解度实验的测定值与文献值[3,9]Fig. 5 Measured values and literature values[3,9] of acetylene solubility in different solvents

为检验本方法测量溶解度数据的准确性，将相同温度下的乙炔溶解度实验数据与文献[3,9]数据拟合为亨利系数进行了对比，亨利定律表达式见式(13)。

式中，H为亨利系数，MPa。

为定量评价本方法所测乙炔溶解度的准性，计算了本实验获得的亨利系数和文献[3,9]的亨利系数的绝对相对偏差（ARD，%），其计算公式见式(14)，各项数据比较见表4。

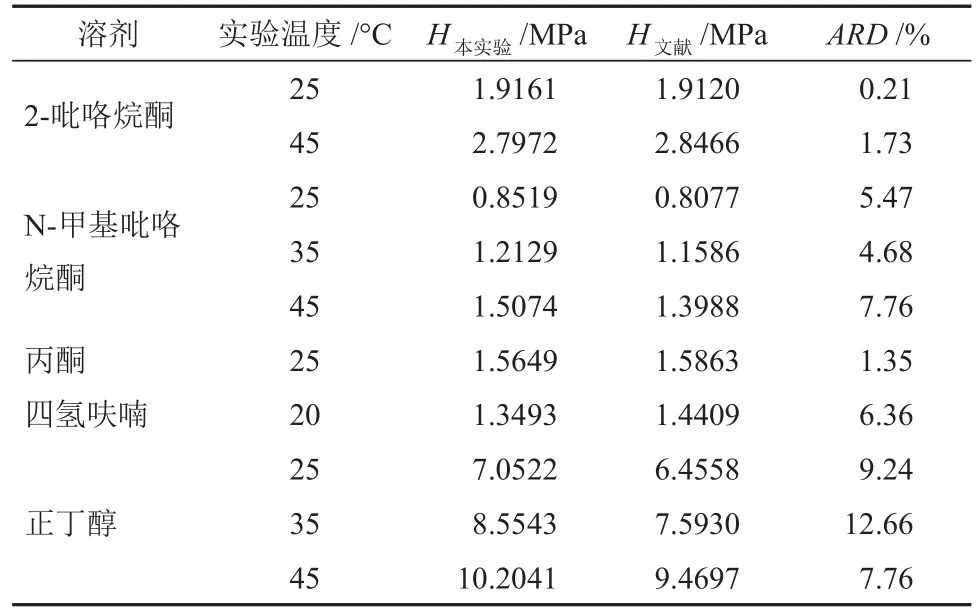
表4 本装置测定的亨利系数与文献［3,9］的亨利系数的比较Table 4 Comparison of Henry coefficients measured by this device and literature［3,9］

在有文献值可参考的温度范围内，本装置测定的亨利系数与文献的亨利系数的平均绝对相对偏差为5.72%，说明通过本方法可以实现乙炔在不同有机溶剂中溶解度的准确测量，包括乙炔易溶溶剂（如N-甲基吡咯烷酮）与乙炔不易溶溶剂（如正丁醇）。除了常温低压的乙炔溶解度测量，本实验还测量了高温、加压条件下的溶解度数据，最高溶解度测量温度达150 °C，最大压力约为0.5 MPa。

为了进一步验证高温溶解度实验结果的可靠性，以25～150 °C下乙炔在2-吡咯烷酮中的溶解度测量结果（图5(a)）为例，计算了不同温度下的亨利系数并进行了热力学分析检验。标准溶解吉布斯自由能（ΔsolGθ，J/mol）与亨利系数的关系，见式(15)，由此得到标准溶解焓变（ΔsolHθ，J/mol），见式(16)。假设溶解焓变不随温度变化，对式(16)积分可以得到式(17)。

式中，C为积分常数。

乙炔在2-吡咯烷酮中的亨利系数与温度之间关系的热力学拟合结果见图6。由图6 可知，ln (H/p0)与1/T呈线性关系，与式(15)符合，说明此装置对高温下的乙炔溶解度测量结果是可靠的。由拟合结果可知斜率ΔsolHθ/R为-2262.9，进而得到乙炔在2-吡咯烷酮中的溶解焓变为18.8 kJ/mol。