预压缩气垫包装系统静力及动力学特性研究

李广利，李玲*，张滔，卞强，王栋彬，刘新丽

预压缩气垫包装系统静力及动力学特性研究

李广利1,2，李玲1,2*，张滔1,2，卞强1,2，王栋彬1，刘新丽1

（1.中国航天员科研训练中心，北京 100094； 2.人因工程全国重点实验室，北京 100094）

以柱形气垫包装系统为研究对象，建立静力及动力学模型，对静态压缩、自由振动和基础激励受迫振动特性进行研究。建立气柱压缩力数学模型，并通过试验、仿真验证模型，通过建立预压缩柱形气垫包装系统力学模型，研究静力及动力学特性。预压缩量和充气压力越大，包装系统固有频率越高。在包装对象宽度定值约束下，选取多个小直径气柱，固有频率更高，且薄膜应力更小。在基础激励下，包装系统固有频率处存在共振峰值，对高频域气垫表现出了较好的减振特性。所建立的静力压缩模型与试验、仿真结果较吻合，所建立的动力学模型合理，结果准确。

柱形气垫；预压缩模型；动力学模型；动力学特性

空气垫是一种常用的包装缓冲材料，它是由塑料薄膜经热合而成的矩形气袋，在使用前充入一定压力的空气，形成柱形充气垫。充气垫轻质、价格低廉且弹性好，具有缓冲、隔音、隔震等特点，应用广泛。

空气垫本质上是一种空气减振弹簧，是利用压缩气垫内的气体产生变形来吸收外界能量，从而获得缓冲保护功能，其缓冲性能主要受到充气压力、气室直径及长度等因素影响。目前较多学者对其耐受冲击的缓冲特性进行了研究。Sasaki等[1]对薄膜空气衬垫进行了静态和动态压缩试验；沈剑锋等、赵德坚等、谷吉海等[2-9]对充气垫冲击缓冲性能进行了试验研究，研究了充气压力、几何尺寸对缓冲性能的影响；郭振斌[10]建立了单自由度单层气垫包装系统动力学方程，对振动和冲击机理及特性进行了理论研究。另外陈鸣等[11]、任冬远等[12]、吴芳英等[13]对充气垫的静态压缩模型、特性进行了理论及试验研究；巩桂芬等[14-15]对破损强度进行了研究。

面对航空航天飞行器所承载的货物，其所经受的力学环境除了冲击外，振动环境也尤为恶劣。对充气垫振动环境的特性研究相对较少，且在预压缩条件下的特性研究目前还是空白。本文对预压缩空气垫包装系统静力及动力学特性进行研究，为其应用提供理论支持。

1 柱形气柱压缩模型

1.1 压缩模型

空气垫由多个柱形气柱构成，每个气柱相互独立，取单个气柱为研究对象，建立压缩位移和压缩力的数学模型。单个柱形气柱几何模型如图1所示。压缩过程材料弹性变形微小，忽略不计[3]。

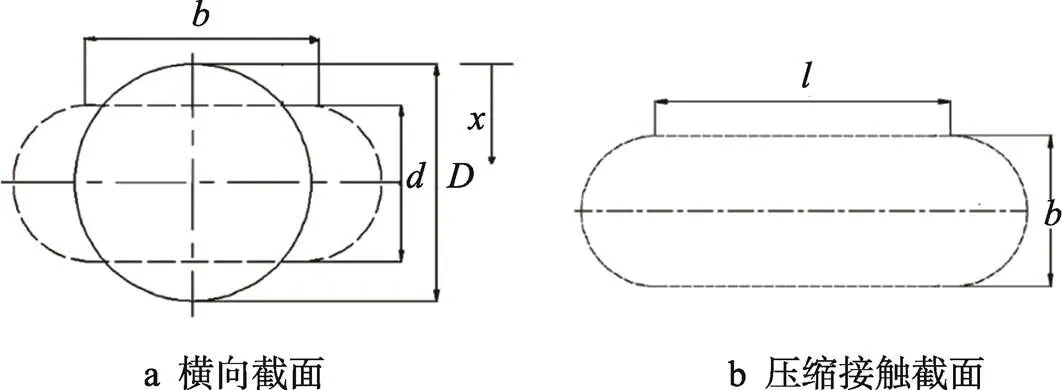
图1 柱形气柱几何模型

图1中、分别为气柱压缩前后的厚度，为压缩后接触面积的宽度，为气柱柱段长度，为气柱压缩变形量，则有式（1）：

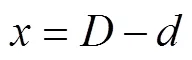
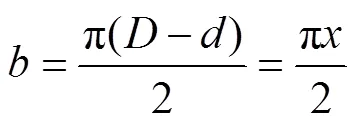
压缩接触截面面积为：

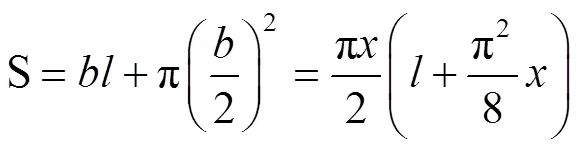
压缩前后因体积变化，气柱内部压力产生变化，气柱两端部位体积相对较小，忽略不计。压缩前气柱体积为：

压缩后气柱体积为：

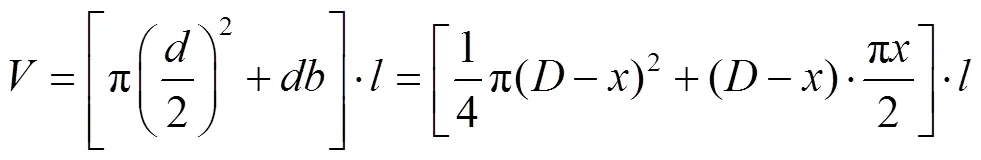
压缩前后体积比为：

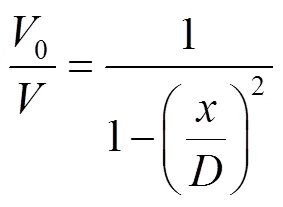
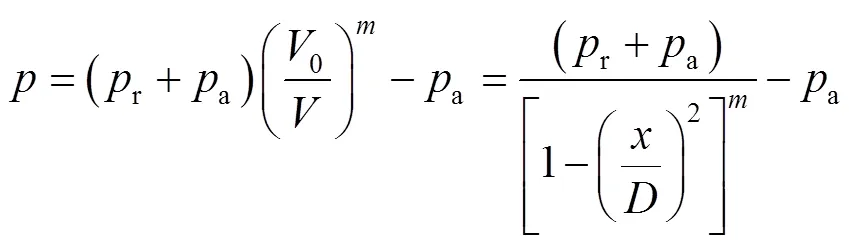
其中为多变系数，准静态压缩过程中空气垫内气体变化为等温过程，取=1；振动过程压缩气体状态变化可近似认为是绝热过程，取=1.4。

柱形气垫压缩过程的受力见图2。内部气体的相对气压为，若空气垫数量为，由力平衡得到压缩力为：

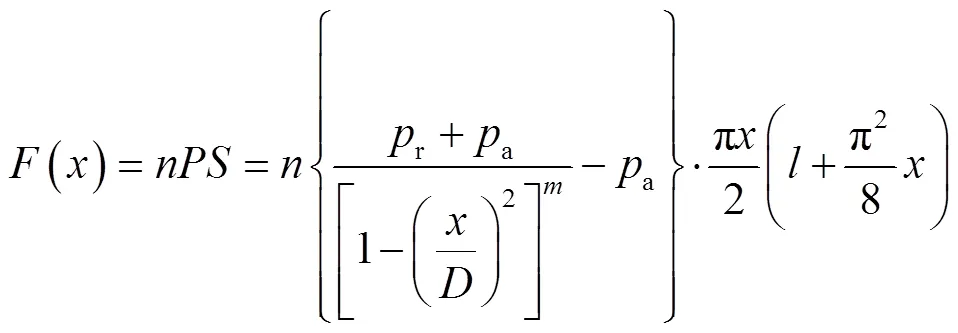
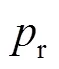
1.2 模型验证

通过试验及数值仿真，对式（8）进行验证。

试验验证选取3个气室柱形气垫，保证试验数据一致性。气柱充气后厚度为18.2 mm，长度为156 mm，其中有效圆柱段长度为150 mm，实验设备选用LRX PLUS型电子材料试验机，精度为0.5%。取3组3个气室柱形气垫，使用压缩空气充气，充气压力分别为20、40、60 kPa，试验加载速率为10 mm/s，进行准静态压缩试验。

数值仿真验证采用有限元分析工具Abaqus，对空气垫静态压缩进行力学仿真模拟。根据对称关系建立1/8对称模型，并设置对称约束关系，如图3所示。气柱采用M3D4膜单元模拟，膜材料弹性模型为1 GPa，泊松比为0.45；充气腔体采用fluid cavity模拟，环境压力设置为101.325 kPa；设置3种充气压力工况，分别为20、40、60 kPa，施加载荷为位移，计算得到反作用力，即压缩力的结果。

图3 柱形气垫有限元对称模型

对20、40、60 kPa 3种初始充气压力气柱物理模型、试验、数值仿真的压缩力-压缩位移数据进行对比，见图4。结果表明，三者数据吻合较好，本文模型能够较准确地反映柱形气柱静态压缩特性。

1.3 气柱数量与等效应力关系

在实际使用中，在预压缩力、包装对象宽度尺寸定值约束下，选取个数多直径较小的气垫，还是选取个数少但直径较大的气垫更好，有必要进行分析，为实际使用提供参考。

不同直径下气柱受压后其内压、薄膜应力也会存在一定的变化。应力直接影响气柱的承载能力，应力越小，包装系统可靠性越高。

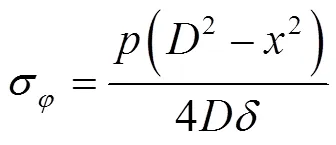
周向应力为：

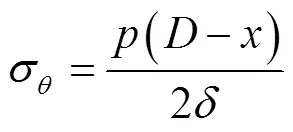
则Von-Mises等效应力为：

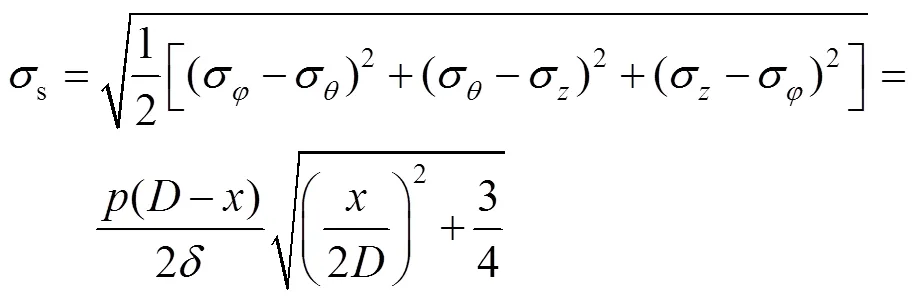
式中：为气柱内压；为气柱直径；为气柱薄膜材料厚度。

取压缩力=600 N，包装对象宽度=200 mm，气柱长度=150 mm，气柱薄膜厚度=0.1 mm，充气压力r取20、40、60 kPa 3种工况，气柱个数为，气柱直径=/，由式（8）求得压缩量，由式（7）求得气柱内压，由式（11）得到等效应力。气柱数量与等效应力关系如图5所示。

由图5可知，气柱数量越多，气柱薄膜应力越低，气柱数量到一定程度后，应力变化较小。实际使用中，较小的气柱直径意味着较小的缓冲压缩量，应根据包装对象尺寸、缓冲需求等选取合适直径尺寸的空气垫。

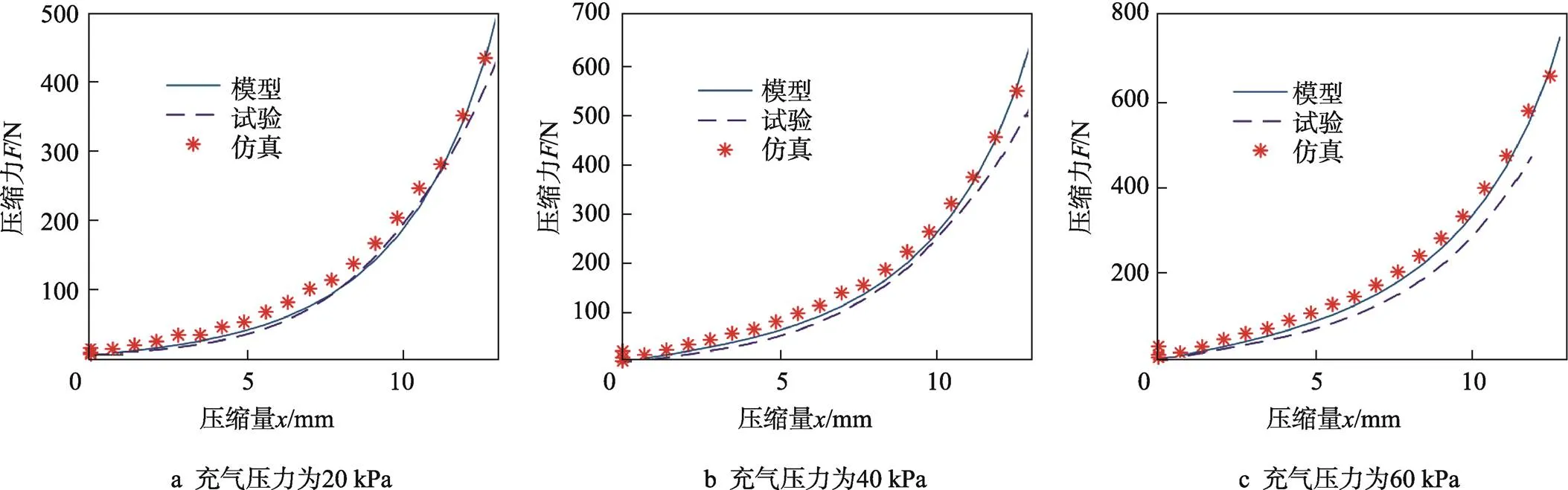
图4 模型、仿真、试验比较

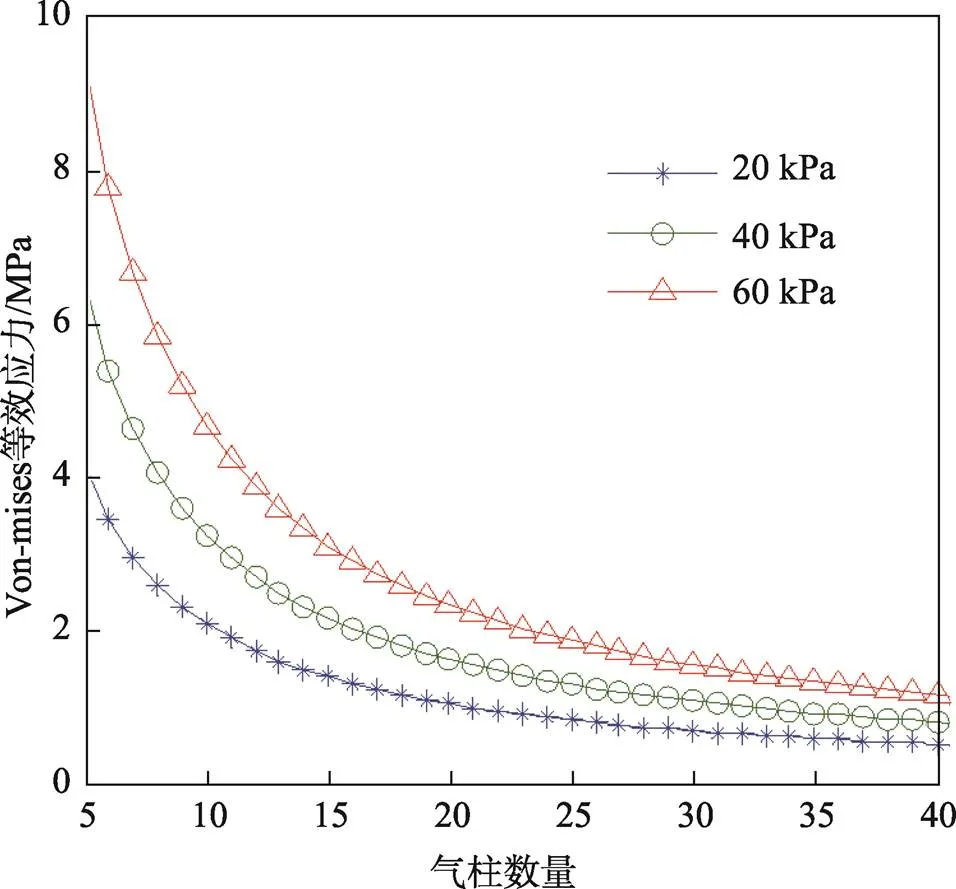
图5 气柱数量与等效应力的关系

2 预压缩气垫包装系统

2.1 数学模型

实际的包装系统，一般使用多个连体空气垫将包装对象包裹。为减轻包装对象在运输过程中晃动，一般将外包装内的空气垫压紧后封装，使得空气垫形成一定程度的预压缩，与包装对象和外包装紧密贴合，达到较好的限位作用，形成由包装对象、空气垫、外包装组成的包装系统。

对包装系统进行受力分析，将其进行简化，几何模型如图6所示。其中上层空气垫数量为1，直径为1，充气压力为r1，气柱长度为1，下层空气垫数量为2，直径为2，充气压力为r2，气柱长度为2。

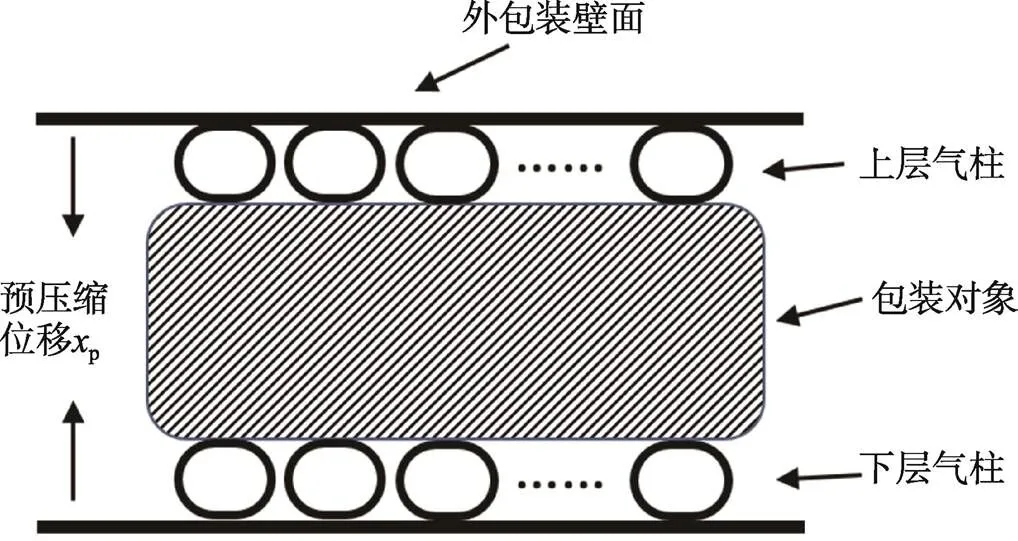
图6 包装系统几何模型

包装系统空气垫初始的总预压缩量为p，上层空气垫初始预压缩量为p1，下层空气垫初始预压缩量为p2，则：

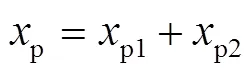
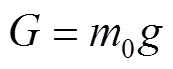
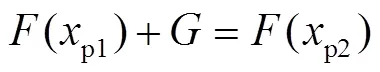
将p1、p2代入式（8），由式（9）、式（10）可求出p1、p2。

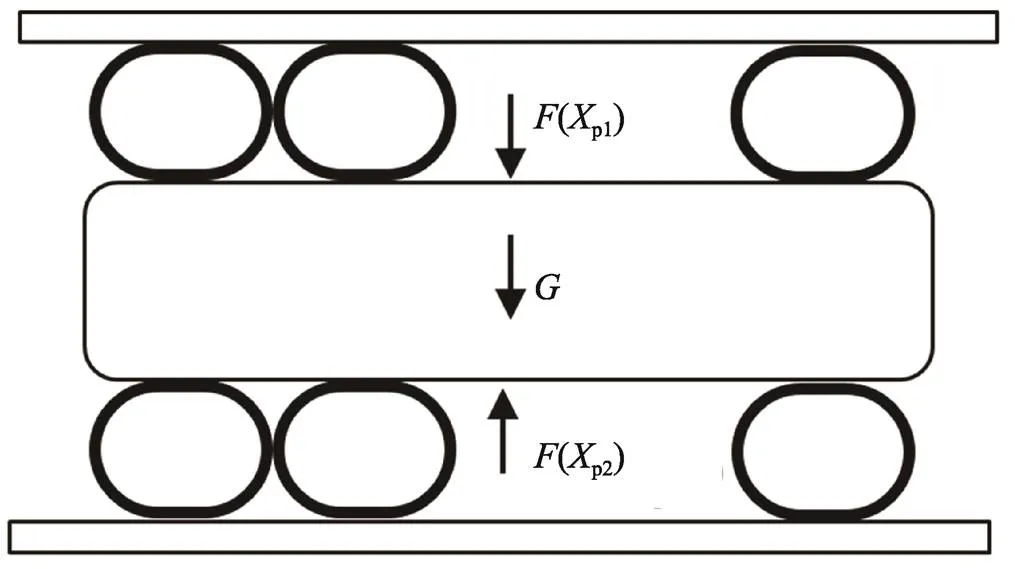
图7 包装对象受力关系

对于水平方向，无重力作用，即=0，可求出p1、p2。若两侧的空气垫数量、直径、充气压力、气柱长度均相同，则p1=p2。对于无预压缩的空气垫，即(p1)=0，可通过式（10）求出下层空气垫仅在重力作用下的压缩量。

2.2 预压缩量与气柱应力关系

对空气垫施加预压缩量，会使得气柱内压增大，从而增大气柱薄膜的等效应力。若预压缩量施加过大，存在气柱破坏失效的风险。对于重力方向，下层气柱比上层气柱需额外承受包装对象的重力作用，其内压大于上层气柱，因此对下层气柱进行应力分析。

取包装对象质量10 kg，上、下层气柱完全相同，充气压力取20、40、60 kPa 3种工况，气柱长度为150 mm，气柱薄膜厚度为0.1 mm，气柱直径为18 mm，气柱个数为10，计算不同预压缩量下气柱薄膜应力。由式（12）、式（13）可求出上、下层气柱压缩量，由式（5）求得下层气柱的内压，由式（11）求得下层气柱薄膜的等效应力。计算得到预压缩量与等效应力关系曲线如图8所示。

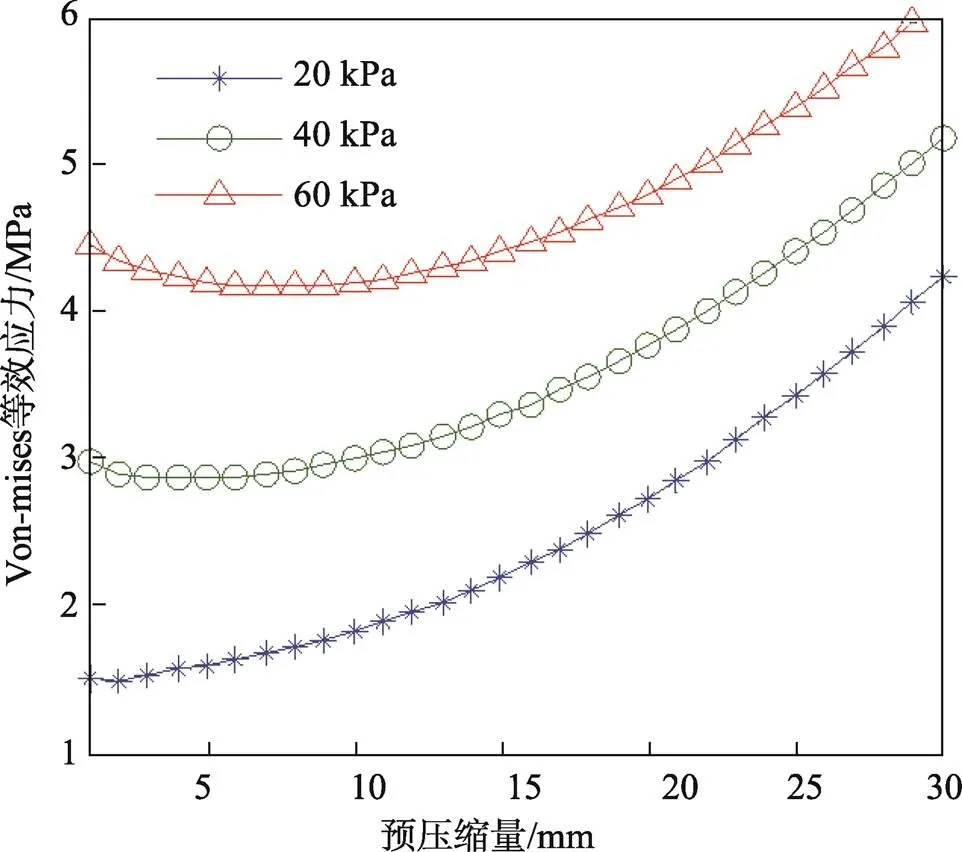
图8 预压缩量与等效应力的关系

图8表明，在重力作用下，薄膜具有初始应力，而后随预压缩量的增大，等效应力随之增大，预压缩量大于10 mm后与气柱薄膜等效应力近似为线性关系。

2.3 包装对象加速度与气柱应力关系

包装对象加速度的增加，会使得下层气柱内压增大，从而增大气柱薄膜的等效应力。对于航空、航天超高音速飞行器，存在较大的过载，加速度一般为8左右。包装系统在较大的加速度下，存在气柱破坏失效的风险，有必要对此进行分析。

取包装对象质量10 kg，上、下层气柱完全相同，充气压力取20、40、60 kPa 3种工况，气柱长度为150 mm，气柱薄膜厚度为0.1 mm，气柱直径为18 mm，气柱个数为10，预压缩量为10 mm，计算不同加速度下气柱薄膜应力。由式（12）、式（13）可求出上、下层气柱压缩量，由式（5）求得下层气柱内压，由式（11）求得下层气柱薄膜的等效应力。计算得到加速度与等效应力的关系曲线如图9所示。

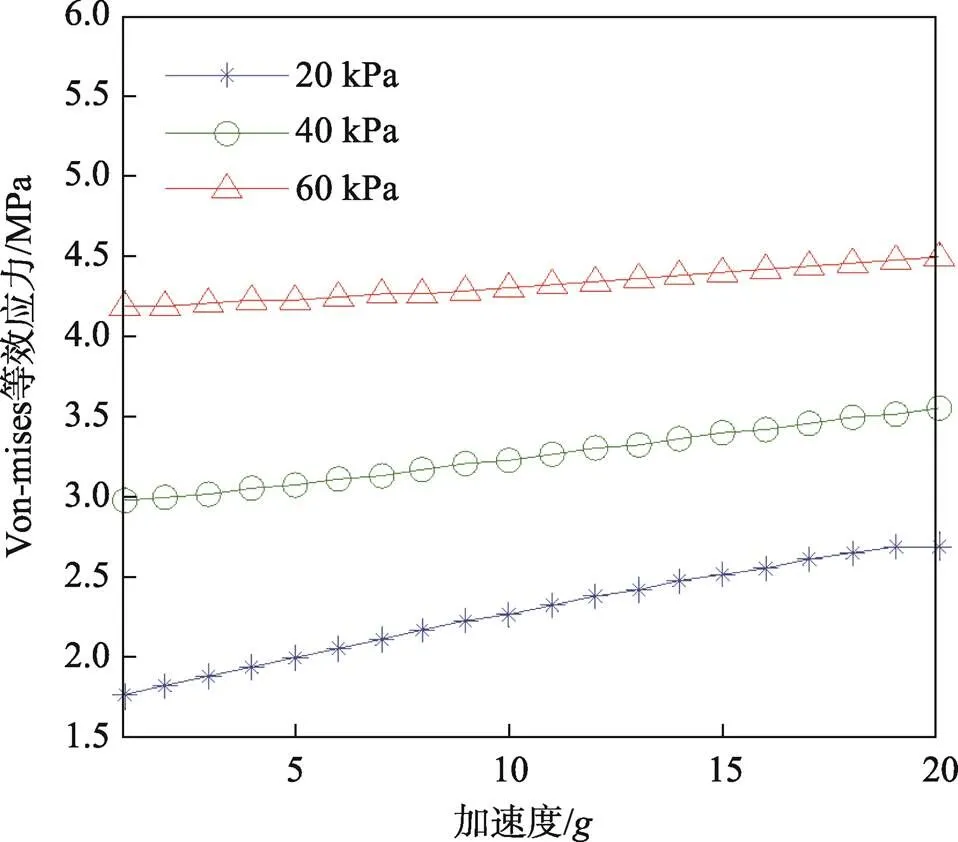
图9 加速度与等效应力的关系

图9表明，随着充气压力的增大，气柱薄膜应力对重力敏感度下降，随着加速度的增加，薄膜应力增幅较小，薄膜应力的主要来源为充气压力，重力次之。

3 动力学模型

为研究预压缩柱形包装系统动力学特性，忽略气垫的质量，包装对象的刚度相对气垫较大，简化为刚体。将外包装壁面假设为刚性，可将其等效为单自由度非线性振动系统，如图10所示。

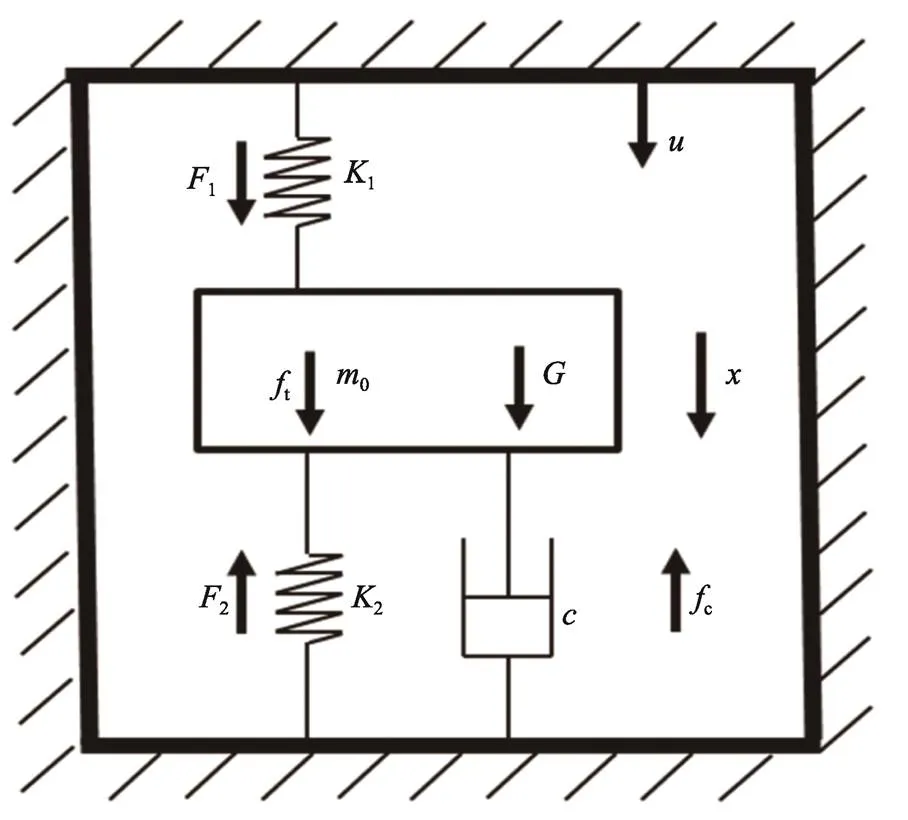
图10 包装系统力学模型

包装系统自由振动状态下，惯性力为：

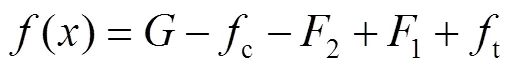
即得到预压缩柱形包装系统非线性动力学方程为：

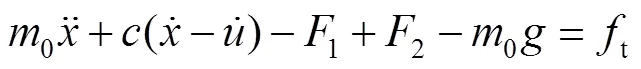
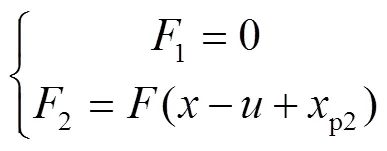
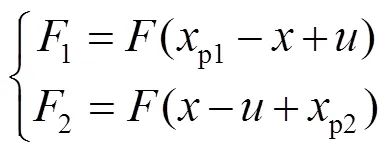
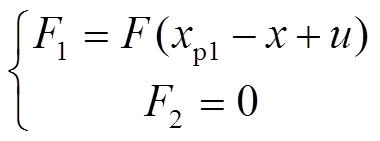
4 动力学特性

4.1 自振特性

4.1.1 动力学方程

不考虑阻尼以及包装对象上的激励力，即c、t为0，自由振动状态无基础激励0，即预压缩柱形包装系统自由振动方程为：

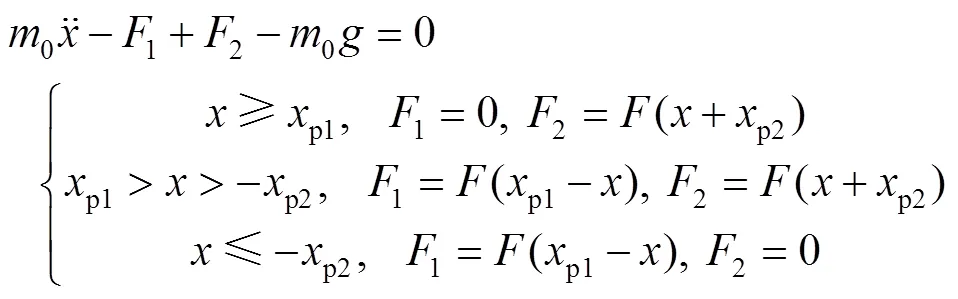
给定初始位移为、初始速度为0，即初值条件为：

将式（19）二阶偏微分方程转换为一阶偏微分方程组为：

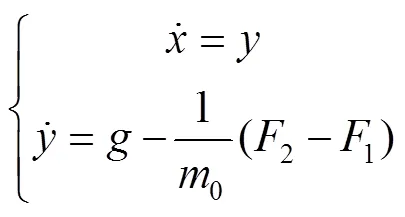
使用数值解法四阶龙格-库塔法，代入式（20）初值条件，可对式（21）进行求解，本文通过MATLAB中ODE45函数求解。通过数值求解得到的位移响应()，该响应具有周期性，相邻峰值时间差即为系统自振周期，系统固有频率为1/。

气垫包装系统的振动存在非线性特性，系统自振固有频率将受到气柱的结构参数及初始条件的影响。对此进行分析，可为包装系统的设计提供参考。

4.1.2 振幅对固有频率影响

气垫包装系统为非线性振动系统，其固有频率与包装对象振幅有关。取包装对象质量10 kg，上、下层气柱完全相同，充气压力取20、40、60 kPa 3种工况，气柱长度为150 mm，气柱直径为18 mm，气柱个数为10，预压缩量为10 mm，计算振幅与固有频率关系，结果如图11所示。

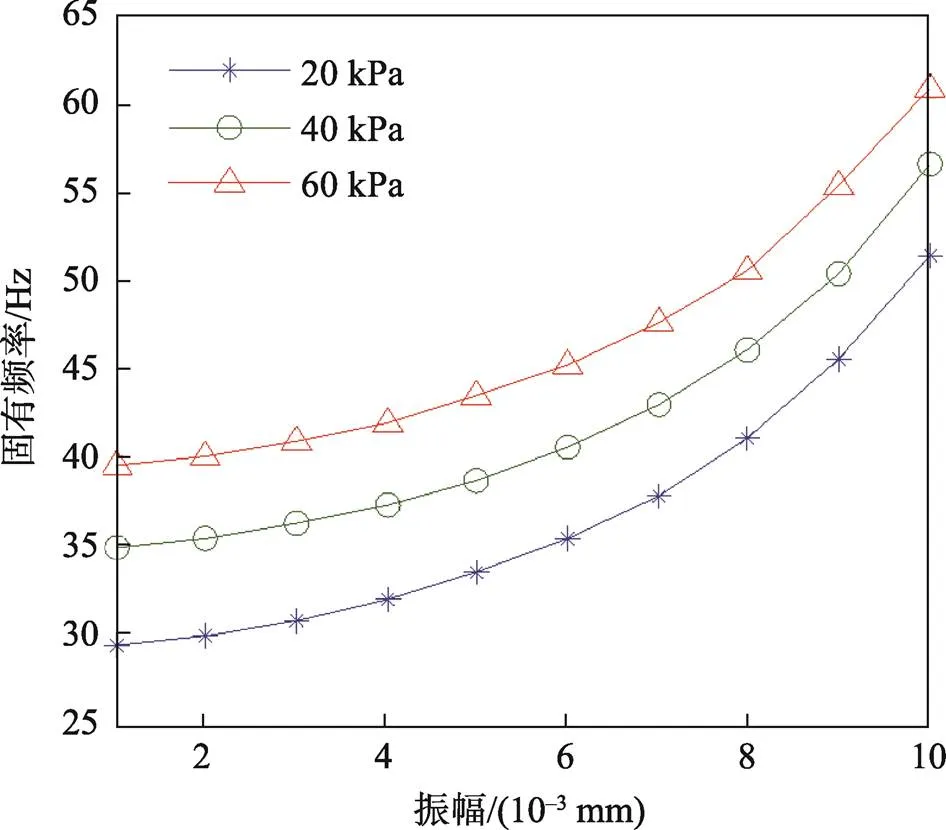
图11 振幅与固有频率关系

图11表明，充气压力越大，固有频率越高，振幅越大，固有频率越高，实际使用中可通过控制充气压力来调节包装系统的固有频率，避免与运载系统发生频率耦合。

4.1.3 气柱数量对固有频率影响

在压缩力、包装对象宽度定值条件下，气柱个数越多，直径越小，包装系统的固有频率也会发生变化。取压缩力=600 N，包装对象宽度=200 mm，气柱长度=150 mm，充气压力r取20、40、60 kPa 3种工况，气柱个数为，气柱直径=/，初始位移取2 mm，对式（19）数值求解，计算得到气柱数量与固有频率关系曲线如图12所示。

图12表明，随着气柱数量的增大，系统固有频率升高。当气柱数量约低于9个时，充气压力越大，系统固有频率越大；当气柱数量约高于9个时，充气压力越大，系统固有频率反而越小。

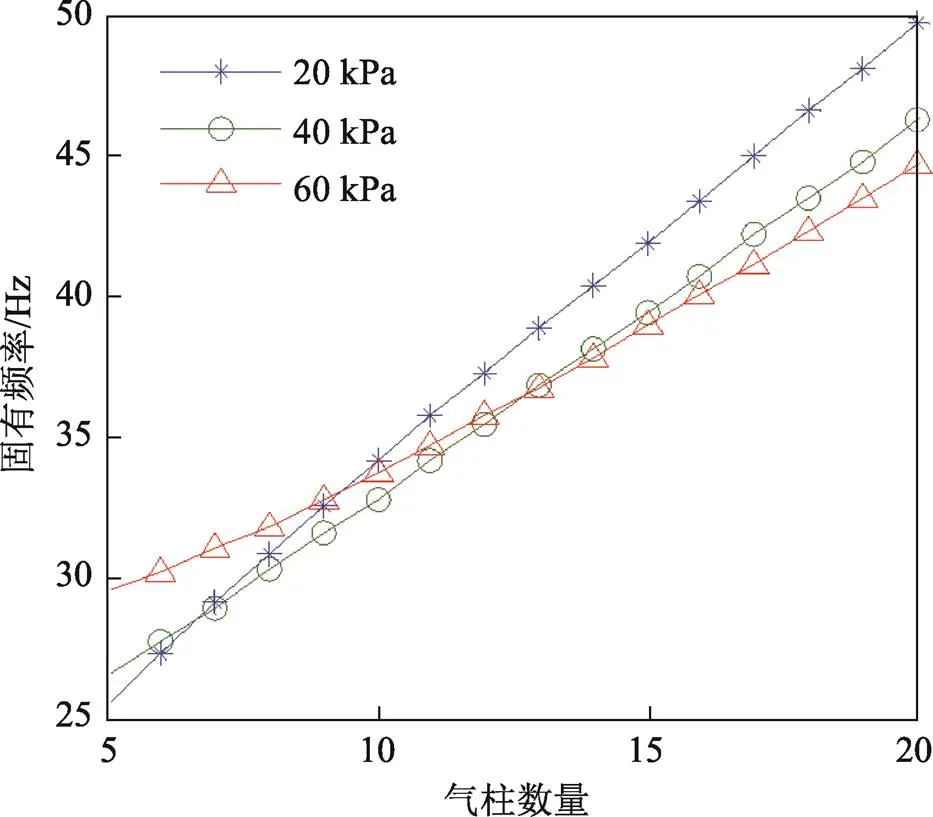
图12 气柱数量与固有频率关系

4.1.4 预压缩量对固有频率影响

对空气垫施加预压缩量，会使得气柱内压增大，包装系统刚度增大。取包装对象质量10 kg，上、下层气柱完全相同，充气压力取20、40、60 kPa 3种工况，气柱长度为150 mm，气柱直径为18 mm，气柱个数为10，初始位移取2 mm，计算不同预压缩量下包装系统固有频率，计算得到预压缩量与固有频率关系曲线如图13所示。

图13表明，随着预压缩量的增大，系统固有频率同步增大。这是因为预压缩量的增大，使用的气柱内气体压力增高，从而增加了气柱刚度，使得固有频率增大。

4.2 基础激励受迫振动

4.2.1 动力学方程

对于基础激励受迫振动，不考虑阻尼以及作用在包装对象上的激励力，预压缩柱形包装系统受迫振动方程见式（22）。

图13 预压缩量与固有频率的关系

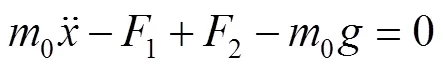
给定初始位移为0、初始速度为0，即初值条件为：

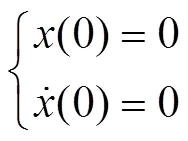
使用四阶龙格-库塔法可将式（22）进行求解。

在包装系统运输过程中，不可避免要承受外部振动，此时包装对象会产生相应的动响应。降低包装对象的动响应是包装系统的设计目的之一，使其处于良好的力学环境，起到防护作用。外部振动的输入、气柱数量、预压缩力等都会影响包装对象动响应，需对其进行分析，为包装系统设计提供参考。

4.2.2 加速度响应分析

包装对象的加速度响应表征其受到惯性力的大小，即包装对象经受的力学环境情况。取包装对象质量10 kg，上、下层气柱完全相同，充气压力取20、40、60 kPa 3种工况，气柱长度为150 mm，气柱直径为18 mm，气柱个数为10，预压缩量为10 mm，基础激励输入为1平直谱，计算加速度动响应，结果如图14所示。

图14表明，在包装系统固有频率处存在共振峰值，充气压力越大，包装系统刚度越大，固有频率越高。对大于65 Hz的高频域，气垫表现出了较好的减振特性。

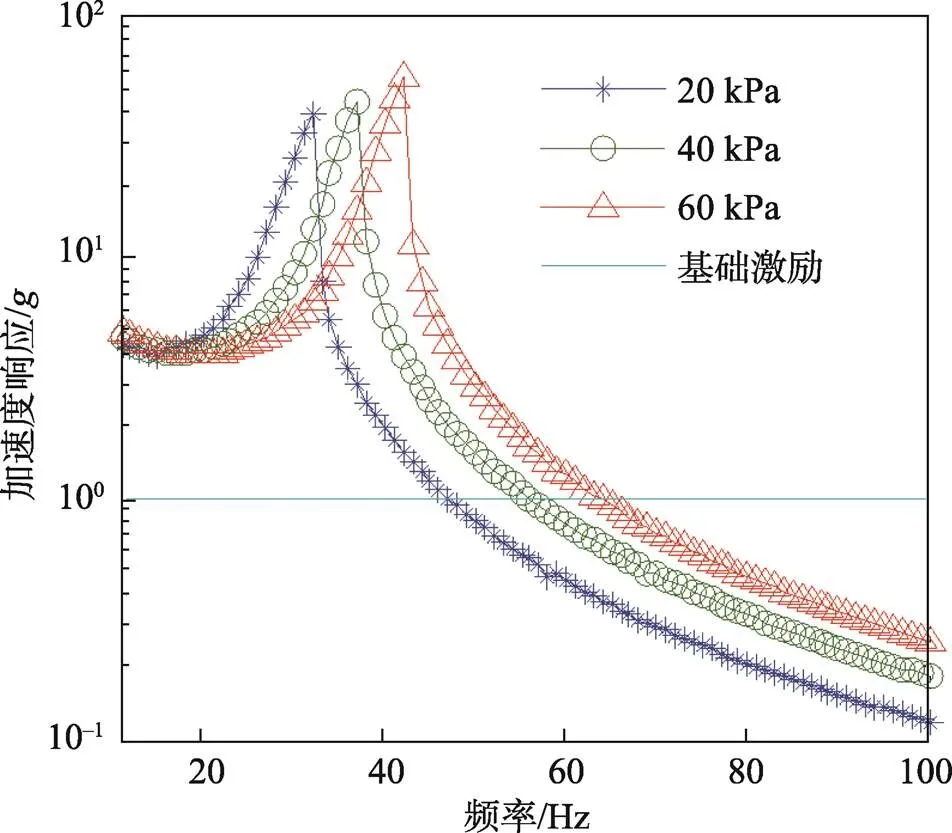
图14 加速度动响应

4.2.3 气柱数量对动响应影响

由第4.1.3节分析得到，在包装对象宽度一定的约束条件下，选取多个小直径气垫，包装系统的固有频率更高，对此进行动响应分析。

取压缩力=600 N，包装对象宽度=200 mm，气柱长度=150 mm，充气压力r取40 kPa，气柱个数取5、10、20这3种工况，气柱直径=/，即分别为40、20、10 mm，基础激励输入为1平直谱。对式（22）数值求解，计算得到不同气柱数量的加速度响应曲线，如图15所示。

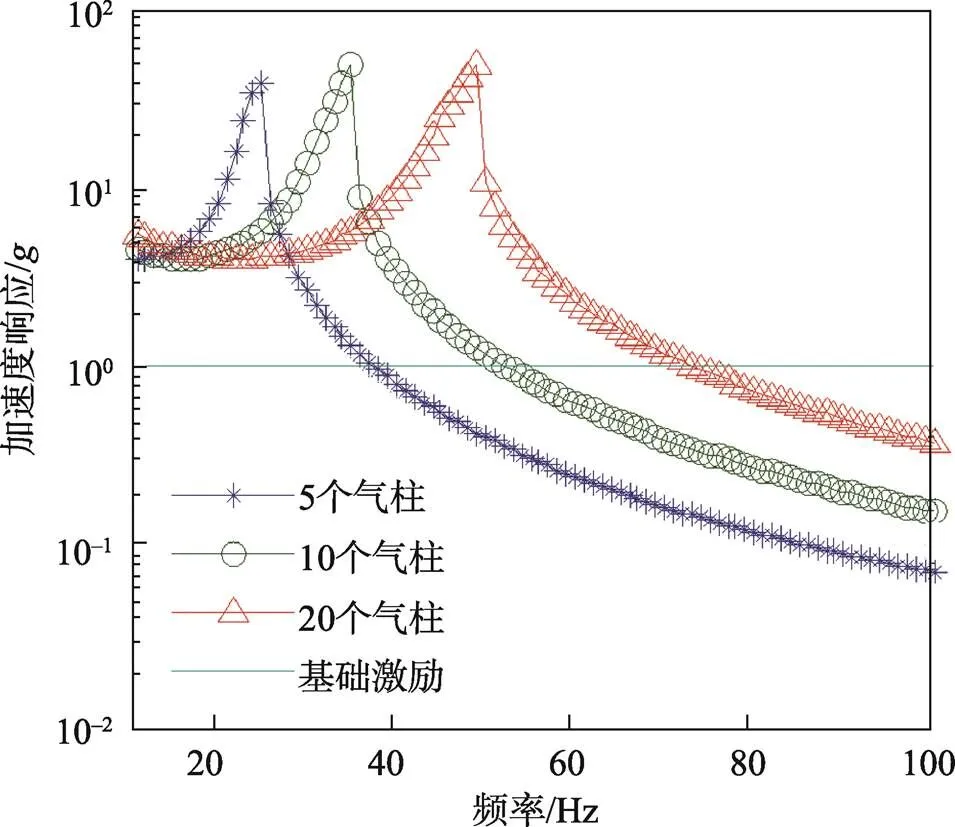
图15 气柱数量与动响应的关系

图15表明，相比之下，多个小直径气垫方案的包装系统固有频率更高，但加速度响应峰值相近。

4.2.4 预压缩量对动响应影响

由4.1.4节分析得到，随着预压缩量的增大，系统固有频率同步增大，对此进行动响应分析。取包装对象质量10 kg，上、下层气柱完全相同，充气压力为40 kPa，气柱长度为150 mm，气柱直径为18 mm，气柱个数为10，预压缩量取5、10、15 mm 3种工况，基础激励输入为1平直谱，计算得到不同预压缩量下包装对象的加速度响应曲线，如图16所示。

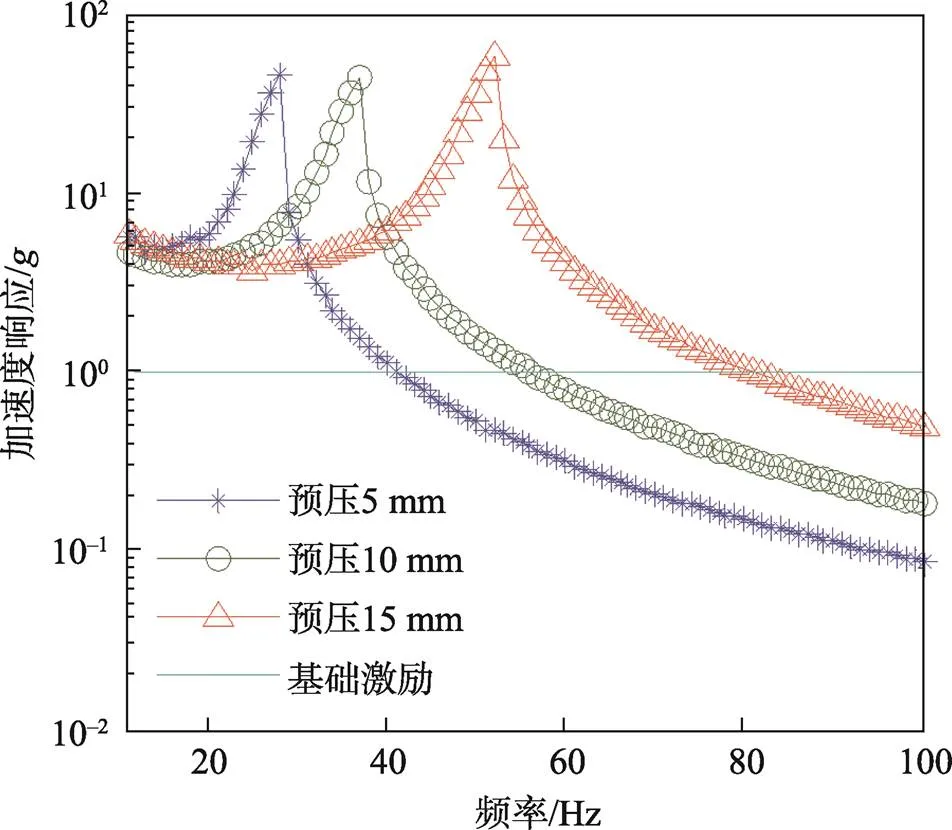
图16 预压缩量与动响应的关系

图16表明，预压缩量增大，系统固有频率增大，但响应峰值相近。预压缩量由10 mm增至15 mm，与气柱数量由10个增至20个所提升的刚度相近，但均大于充气压力由40 kPa提高至60 kPa所提升的刚度。因此通过增加预压缩量来提高系统刚度方法更有效。

5 结语

通过对预压缩柱形气垫包装系统静力及动力学特性分析发现，预压缩量越大，包装系统固有频率越高，但气柱薄膜应力也随之增大。在包装对象宽度定值约束下，选取多个小直径气柱，包装系统固有频率更高，且气柱薄膜应力更小。包装系统为非线性振动系统，位移振幅越大，系统固有频率越大。通过分析表明，气垫充气压力越大，系统固有频率越大。在基础激励下，包装系统固有频率处存在共振峰值，对高频域气垫表现出了较好的减振特性。

在实际使用中应通过调节充气压力、气柱数量、预压缩量3个参数来调节包装系统的固有频率，与运载系统的固有频率错开，避免发生耦合。可通过分析包装对象加速度响应值，对比其脆值，评估气垫包装系统所提供的力学环境是否满足其需求。

[1] SASAKI H, SAITO K, ABE K. Development of an Air Cushioning Material Based on a Novel Idea[J]. Packaging Technology and Science, 1999, 12(3): 143-150.

[2] 沈剑锋. 空气垫基本力学与缓冲性能试验研究[D]. 无锡: 江南大学, 2008: 1-21.

SHEN J F. Experimental Study on Basic Mechanics and Cushioning Performance of Air Cushion[D]. Wuxi: Jiangnan University, 2008: 1-21.

[3] 赵德坚. 充气量对充气缓冲包装垫缓冲性能的影响研究[J]. 包装工程, 2011, 32(13): 32-34.

ZHAO D J. On Influence of Gas Volume on Cushioning Property of Air Cushion[J]. Packaging Engineering, 2011, 32(13): 32-34.

[4] 谷吉海, 田野, 高翔, 等. 充气压力对空气衬垫缓冲防护性能的影响研究[J]. 振动与冲击, 2016, 35(20): 226-230.

GU J H, TIAN Y, GAO X, et al. Research on the Effect of Inflation Pressure on the Cushion Protection Performance of Air Cushions[J]. Vibration and Shock, 2016, 35(20): 226-230.

[5] 王慧. 空气衬垫的缓冲防护机理与冲击特性研究[D]. 哈尔滨: 哈尔滨商业大学, 2014: 33-38.

WANG H. Study on Cushioning Protection Mechanism and Impact Characteristics of Air Cushion[D]. Harbin: Harbin University of Commerce, 2014: 33-38.

[6] 范珺. 空气垫缓冲包装承载性验证及影响分析[J]. 上海包装, 2016(6): 41-42.

FAN J. Carrying Capacity Verification and Impact Analysis of Air Cushion Packaging[J]. Shanghai Packaging, 2016(6): 41-42.

[7] 周加彦, 范珺. 空气垫缓冲包装承载性验证及影响分析[J]. 中国包装, 2016, 36(5): 48-50.

ZHOU J Y, FAN J. Carrying Capacity Verification and Impact Analysis of Air Cushion Packaging[J]. China Packaging, 2016, 36(5): 48-50.

[8] 陈梓垠, 王玉龙, 梁秀. 空气柱衬垫缓冲性能研究[J]. 绿色包装, 2017(9): 51-55.

CHEN Z Y, WANG Y L, LIANG X. Research on Cushioning Properties of Air Tube Pillow[J]. Green Packaging, 2017(9): 51-55.

[9] 梁秀. 空气柱衬垫缓冲性能研究[D]. 武汉: 武汉大学, 2017: 42-49.

LIANG X. Study on Cushioning Performance of Air Column Gasket[D]. Wuhan: Wuhan University, 2017: 42-49.

[10] 郭振斌. 缓冲气垫包装系统振动机理及特性研究[D]. 无锡: 江南大学, 2012: 19-24.

GUO Z B. Study on Vibration Mechanism and Characteristics of Cushion Air Cushion Packaging System[D]. Wuxi: Jiangnan University, 2012: 19-24.

[11] 陈鸣, 彭雄奇, 石少卿, 等. 薄膜超弹性本构模型及其在空气垫中的应用[J]. 上海交通大学学报, 2014, 48(6): 883-887.

CHEN M, PENG X Q, SHI S Q, et al. A Hyperelastic Constitutive Model for Membrane and Its Application in Air Cushion[J]. Journal of Shanghai Jiao Tong University, 2014, 48(6): 883-887.

[12] 任冬远. 空气垫在受到跌落冲击时的缓冲机理及性能研究[D]. 无锡: 江南大学, 2008: 27-48.

REN D Y. Study on Cushioning Mechanism and Performance of Air Cushion under Falling Impact[D]. Wuxi: Jiangnan University, 2008: 27-48.

[13] 吴芳英, 范小平, 向红, 等. 空气垫静态缓冲性能的数值模拟[J]. 包装工程, 2015, 36(5): 11-15.

WU F Y, FAN X P, XIANG H, et al. Numerical Simulation of Static Cushion Performance of Air Cushion[J]. Packaging Engineering, 2015, 36(5): 11-15.

[14] 巩桂芬, 刘萌沛. 充气垫缓冲材料破损强度研究[J]. 陕西科技大学学报(自然科学版), 2015, 33(3): 149-153.

GONG G F, LIU M P. Study on the Compressive Strength of Air Filled Cushions[J]. Journal of Shaanxi University of Science & Technology, 2015, 33(3): 149-153.

[15] 巩桂芬, 李超. 柱形空气衬垫振动传递特性的试验研究[J]. 包装工程, 2019, 40(19): 92-96.

GONG G F, LI C. Experimental Study on Vibration Transmissibility Properties of Cylindrical Air Cushion[J]. Packaging Engineering, 2019, 40(19): 92-96.

Static and Dynamic Characteristics of Pre-compression Air Cushion Packaging System

LI Guangli1,2,LI Ling1,2*,ZHANG Tao1,2,BIAN Qiang1,2, WHANG Dongbin1, LIU Xinli1

(1. Astronaut Center of China, Beijing 100094, China; 2. National Key Laboratory of Human Factors Engineering, Beijing 100094, China)

The work aims to establish a static and dynamic model with a cylindrical air cushion packaging system as the research object, to study the characteristics of static compression, free vibration and forced vibration under foundation excitation. A mathematical model for the compression force of the air cushion was established and verified through experiments and simulations. By establishing a mechanical model of a pre-compression cylindrical air cushion packaging system, the static and dynamic characteristics were studied. The dynamic analysis of the packaging system showed that the higher the pre-compression and inflation pressure, the higher the natural frequency of the packaging system. Under the constraint of the fixed width of the packaging object, selecting multiple small diameter air cushion resulted in higher natural frequencies and lower Von-mises stress. Under the foundation excitation, there was a resonance peak at the natural frequency of the packaging system, which showed a good vibration reduction characteristics for air cushion in the high frequency domain. The static compression model established is in good agreement with the experimental and simulation results. The dynamic model established is reasonable and accurate.

cylindrical air cushion; pre-compression model; dynamical model; dynamical characteristic

TB485.1；TB485.2

A

1001-3563(2024)01-0290-09

10.19554/j.cnki.1001-3563.2024.01.034

2023-10-24

人因工程全国重点实验室基金（6142222210901）