培养科学思维 落实核心素养
2020-06-22周子健张迪
周子健 张迪


摘 要:本文通过对液柱(活塞)移动问题的解决方案,探讨在解题过程中培养学生的科学思维.学生易受做题经验的影响,定式地寻找解决问题的思路,但这不是最简捷快速的方案,如果能鼓励学生发散思维,或从数学角度开拓出全新的路径,最终能实现师生教学相长,实现整体要素的科学思维.
关键词:液柱;压强;科学思维
在2017年新修订的《普通高中物理课程标准》中,首次提出了学科核心素养,这是在原有三维目标的基础上的继承与深化,更加强调了学生的整体性和综合表现.科学思维作为其四个组成部分之一,属于新加入的部分,内容与涵义都更加的具体翔实.在模型建构、科学推理、科学论证和质疑创新四个要素中,每个要素对于培养学生科学思维能力都起着至关重要的作用.本文以气体动态问题中的液柱(活塞)移动问题为例,探讨在高中物理教学过程中学生的科学思维的建立与培养,最终以实现全方面的物理核心素养.
1 外部容器位置变化导致的液面移动
托里拆利管作为学生初中阶段最先接触到的,衡量气体压强确切数值的量具模型,在高中阶段依然可以通过其变式模型的建构,帮助学生深刻理解知识.该装置将抽象的气压具体到了模型,同时学生在学习玻意尔定律之后,对于初末状态的参量的关系有了一定理解,学生就可以对状态量进行初步的数值判断,即管内压强的升降情况,空气柱现长度与原长度关系变化,就可以得到玻璃管位置的调节情况,如例1所示.
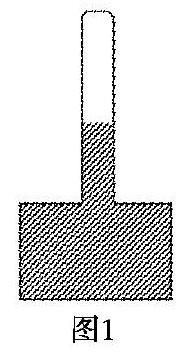
例1 封闭在水银槽内的玻璃管如图1所示,管内水银柱较槽内水银液面的高度差hcm,玻璃管上端的空气柱长度45cm.若要使内外液面相平,问应如何移动玻璃管,同时计算出玻璃管内空气的长度.(此时大气压p0为75cmHg)
解答 管内压强的升高,空气柱现长度比原长度小,所以下调试管.
设p1、p2和L1、L2为初末状态参量,ΔL表示移动的距离,由题意得
p1=p0-h
p2=p0
根据玻意尔定律可得
p1L1=p2L2
计算可得
L2=39.6cm
所以
ΔL=54-39.6=14.4cm
此时空气管的长度为39.6cm,需要将玻璃管向下移动14.4cm.
分析 托里拆利管作为气体压强量具,在有確切数值的情况下,快速建立模型,得到表1所示的情景-状态表.
该情景与状态是互为充分必要条件,即该情景的发生或者该状态下其中一个条件的发生,必将导致对方量的改变.这种模型的建构有助于学生理解状态参量的变化情况,在学生头脑中成为动态模型的存在.构建托里拆利管这一量度模型[1],培养了学生抽象概括出主要因素,抛出次要因素的建构模型的能力,帮助学生建立并且培养科学思维,体会思维过程,引导学生另辟蹊径,更快速地思考和解决问题,如变式1所示.
变式1 一段封闭在水银槽中的玻璃管如图2所示,玻璃管开口向下倒插,管内上端存有空气柱.温度恒定,现将玻璃管绕试管底端顺时针向右旋转一定角度θ(θ<90°),此过程没有外界空气流入,那么此时玻璃管内空气的长度的变化情况为( ).
A.不变 B.变大 C.变小 D.无法确定
解答 旋转后的试管较竖直时,最高位置处更接近水银面,有一小段高度的试管浸没在水银槽中.可以理解为,向下压试管,即试管的位置相对于水银面向下移动,所以管内空气柱的长度变小.
分析 学生受做题思路的影响,依照惯性思维第一步假定水银柱静止.此题亦可以引导学生从分析空气柱或者水银柱的问题中跳脱出来,直接转变思维,思考试管的位置变化,从而判断出空气柱的压强和体积的变化情况.因此,记住托里拆利管这一动态量度模型,可以帮助学生另辟蹊径,更快速地思考和解决问题.
2 内部状态量变化导致的液面移动
假设法是解决气体动态问题最为常用的方法,一般假设初末状态的气体体积不发生变化,根据查理定律的拓展公式进行下一步的计算,可以得知水银柱的移动情况,如例2所示.
例2 如图3所示竖直放置的上细下粗的封闭玻璃管,管内中间位置有水银柱将气体分隔为A、B两部分,初始状态温度相同,现升高相同温度待装置稳定后问此时水银柱的运动方向和ΔpA与ΔpB的大小关系.
解答 装置封闭,则有
ΔVA=ΔVB
设pA、p′A,pB、p′B和T、T′为初末状态参量,水银柱高度为h.初状态气压关系式
pA=pB+ph
所以有
pA>pB
根据查理定律整理得到
Δp=pΔT T
所以得到变化量的大小关系为
ΔpA>ΔpB
又因为
SA>SB
因此得到
ΔpASA>ΔpBSB
所以下端压力的变化量大于上端,最终向上移动.
分析 这种假设的方法可以在计算时减少一个物理量,从而帮助减轻计算量,化难为简,同时结合受力分析,液柱的移动方向即为压力变化量的大小情况.这种科学推理与科学论证,按照流程进行解题,同时建立更加理性科学的思维方式[2].无论既定假设成立与否,都能条理清晰的逐步解决问题,明朗解题思路和提升解题方法,如变式2所示.
变式2 装置如图4所示,A、B气缸内装有一定质量的同种理想气体,气缸上的活塞通过硬杆连接,此时装置达到平衡状态,两装置体积和温度均相同.若此时两个气缸同时升高相同温度,问活塞的移动方向如何.
解答 设pA、p′A,pB、p′B和T、T′为初末状态参量,初状态体积为V,体积的变化量为ΔV.假设向左移动,由理想气体方程得到
pAV T=p′A(V+ΔV) T′
pBV T=p′B(V-ΔV) T′
两式做比得到
pAp′B pBp′A=V+ΔV V-ΔV
此时得到一个通式,若再次假设不移动,得到
pA T=p′A T′
pB T=p′B T′
两式做比得到
pAp′B pBp′A=1
将上式代入通式中,即当ΔV=0时,左右等式仍然成立,则假设成立,硬杆不移动.
分析 学生在学习必修二第六章天体运动章节,掌握了通过数学做比的方法,得到物理量之间的比值数量关系,所以学生很容易想到,做比可以消除温度这一物理状态量,来寻求其他物理量数量关系的思路,再次假设验证结论.学生通常情况下根据以往的做题经验,定式地假设不移动,会遏制了学生的创新性和发散性思维.判别式的假设移动或者不移动,根据不同题型学生开拓思维自主选择,寻找快速解决问题的途径.
液柱(活塞)移动问题蕴含着科学思维的要素,分析每个状态量,再根据所学的公式加以整合分析;抽象出状态量的特征,用以往或者新建构出的模型加以总结概括;比较不同思路对于同一问题的不同解释,大胆创新,再将自己的新思路分门别类;从个别的题目总结方法到一般性质,和一般的原理开拓创新出新的结论.培养学生的科学思维能力,需要教师身体力行,在教授的过程中严密地科学推理与论证,鼓励学生敢于质疑大胆创新以实现整体结构的科学素养.
参考文献:
[1]夏丽.另辟蹊径解决气体中的一类题[J].物理教学,2017,39(01):36-37.
[2]姜炜星.判别式法在气体动态分析中的应用[J].物理教师,2015.36(05):90-91.
(收稿日期:2020-01-13)
