过渡金属元素X(X=Mo,Tc,Ru)掺杂单层GaS的第一性原理研究

周 腾, 钱国林, 梁 前, 陈 蓉, 黄思丽, 谢 泉

(贵州大学 大数据与信息工程学院 新型光电子材料与技术研究所, 贵阳550025)

1 引 言

自2004年单层石墨烯[1]被发现以来，二维材料受到越来越多的关注. 二维材料具有比表面积大、原子级厚度等优点，在物理、化学、生物和电学等[2-5]领域具有广阔的应用前景. 近年来，二维材料硫化镓(GaS)也受到许多研究人员的关注. 作为一种宽禁带层状半导体材料，让二维GaS在许多领域有着良好性质. 实验上，Afaneh等人[6]通过改进传统化学气相沉积(chemical vapor deposition，CVD)方法，利用商业生产的前驱体，制备出连续的GaS单层材料，为其更好地应用到光电子器件中打下了实验基础. Dicorato等人[7]通过机械剥离方法获得了38～1665 nm不同厚度的GaS样品，并对其光响应率等特性进行了测量和分析，发现GaS的光响应率随其厚度的增加而增加. Ahmed等人[8]采用液相剥离法合成了超薄二维GaS纳米片，并在侧抛光光纤上沉积二维GaS纳米片后，首次成功地制备了可饱和吸收器(saturable absorbers，SAs)，在1 μm和1.5 μm时，分别可以实现10%和5.3%的调制深度，表明所制备的SAs的宽带饱和吸收性能良好. Alencar等人[9]同样利用机械剥离方法得到不同层数的GaS样品，并对其拉曼光谱的偏振依赖性进行研究，结果表明拉曼光谱的偏振依赖性与GaS材料的层数变化没有明显关联. 此外，Deckoff-Jones等人[10]将氮化硅(SiN)和GaS材料混合集成，混合后的光波导材料的非线性折射率比SiN光波导材料提升了五倍.

在理论计算方面，Yang等人[11]对单层GaS材料施加极限应力和应变，发现平面杨氏模量均为正数，证明了单层GaS的机械稳定性. Nayeri等人[12]采用第一性原理方法计算了单层GaS在不同本征缺陷浓度情况下的能带结构、介电函数等性质，发现存在两个S空位缺陷时，GaS的能带结构由间接带隙转变为直接带隙，其带隙宽度从2.3 eV降低到1.33 eV，使电子跃迁的能量降低，这为其应用到光电子领域提供了可能性. 与此同时，Akoto等人[13]通过第一性原理方法研究Ga与S空位缺陷时，GaS的气体吸附性能，结果表明存在Ga与S空位缺陷时，层状GaS材料对SO2、NH3和HCN气体具有良好的物理吸附性能，这表明空位是一种捕获小气体分子的高活性催化位点. Sun等人[14]利用第一性原理方法研究了g-C6N6/GaS异质结的光催化反应机理和光学性质，结果表明该异质结构在界面处产生的内建电场有利于电子-空穴对的分离，并具有良好的可见光吸收能力，说明该异质结构是一种良好的光催化材料和太阳能转换材料. 此外，在元素掺杂方面，Bai等人[15]研究了O、Se、Te、Al、In、Sc、Y元素单掺杂和共掺杂对单层GaS的电子结构和光催化性能的影响，研究结果表明Y和Te共掺体系具有良好的水分解性能，在可见光区的吸收系数提高，说明该共掺体系是一种可用于光催化水分解领域的良好催化剂. Chen等人[16]采用第一性原理方法对非金属元素H、B、C、N、O、 F和3d族过渡金属元素V、Cr、 Mn、Fe、Co、 Ni掺杂单层GaS进行了研究，结果表明3d族过渡金属元素由于正的形成能导致不能自发进入单层GaS材料中，H、B、N和F掺杂体系具有1.0 μB的磁矩，而C、O掺杂体系无磁矩产生. 其他元素掺杂单层GaS材料后也具有良好的电学、光学、磁学和气体吸附等[17-23]性能.

由于过渡金属元素的d轨道处于未填满状态，使得过渡金属元素普遍存在多价态，这使其性质与其他元素有明显的差别. 鉴于目前4d族过渡金属元素掺杂单层GaS材料的研究尚未开展，本文对单层GaS进行替位式掺杂，主要研究了过渡金属元素X(X=Mo，Tc，Ru)掺杂单层GaS材料的电子结构、磁性及光学性质. 希望能为单层GaS在自旋电子学材料和光电子材料等领域的应用提供理论依据.

2 计算方法及理论模型

本文采用VASP(Viennaabinitiosimulation package)软件包[24，25]中基于密度泛函理论(density functional theory，DFT)的投影缀加平面波方法(projector augmented wave，PAW)[26]. 用广义梯度近似(generalized gradient approximation，GGA)下的PBE(Perdew-Burke-Ernzerhof)泛函来描述相互作用电子间的交换关联能[27]. 平面波截断能设置为400 eV，电子自洽弛豫的收敛标准设置为1 × 10-6eV，离子弛豫过程中作用在离子上的力小于0.02 eV/Å时，晶格优化完成. 对不可约布里渊区的积分运算采用Monkhorst-Pack方案[28]设置9 × 9× 1的K点网格进行采样.

计算模型以原子比例为1：1的单层GaS原胞为基础，分别沿a基矢和b基矢方向进行扩胞，得到3 × 3 × 1共36个原子的超晶胞结构. 为了消除层与层之间的相互影响，在c轴方向设置20 Å的真空层，在此基础上对GaS进行替位式掺杂. 由于在实验上对S位进行掺杂比对Ga位进行掺杂容易[18]，所以本文采用S位进行替位掺杂，掺杂浓度为5.6%. 过渡金属元素X(X=Mo，Ru，Rh)掺杂单层GaS的俯视图和侧视图如图1所示(为了方便标识，侧视图中内层的Ga-Ga键未展示).

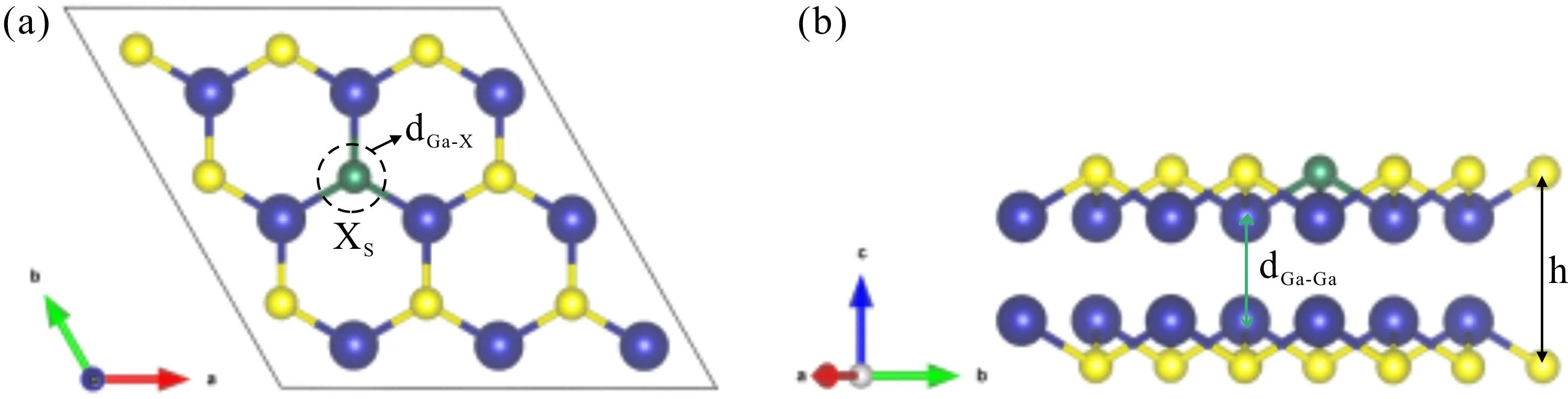
图1 过渡金属原子X(X=Mo，Tc，Ru)掺杂GaS结构示意图(其中黄色球、蓝色球分别代表S原子和Ga原子，绿色球XS代表掺杂原子)：(a)俯视图；(b)侧视图Fig. 1 The structure schematic diagram of transition metal atoms X (X=Mo，Tc，Ru)doped GaS (where the yellow ball and blue ball represent S atom and Ga atom，respectively，and the green ball XS represents the substituted doped atom)：(a)top view；(b)side view

形成能的大小可以体现掺杂体系的相对稳定性，掺杂体系的形成能Ef定义如下[29，30]：

Ef=Etot(GaS+X)-Etot(GaS)+μS-μX

(1)

其中，Etot(GaS+X)代表不同掺杂体系的总能量，Etot(GaS)代表未掺杂GaS超胞的总能量，μX表示掺杂原子X平均化学势，μS代表被取代S原子的平均化学势.对于掺杂原子X，参考相为其对应的块体结构；对于被替代的S原子，参考相为其稳定的S2单质. 根据材料的不同生长情况，μS的大小受Ga-rich和S-rich两种条件约束，具体定义如下：

(2)

(3)

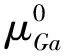
(4)

其中μGaS代表GaS原胞的化学势，其值为Etot(GaS)的1/18.

3 结果与讨论

3.1 几何结构与稳定性

从图1可以看出，单层GaS是由四层原子平面组成，外层为S原子，内层为Ga原子，呈S-Ga-Ga-S的上下对称结构. 其中，dGa-X表示Ga原子与过渡金属掺杂原子X之间的键长，dGa-Ga代表内平面Ga原子之间的相对距离，h表示外层S原子之间的相对距离(即单层GaS的厚度). 掺杂体系与未掺杂体系优化后的结构参数均列于表1，其中a(=b)表示优化后的晶格常数，Ef(Ga-rich)和Ef(S-rich)分别表示在Ga-rich条件下的形成能和S-rich条件下的形成能.

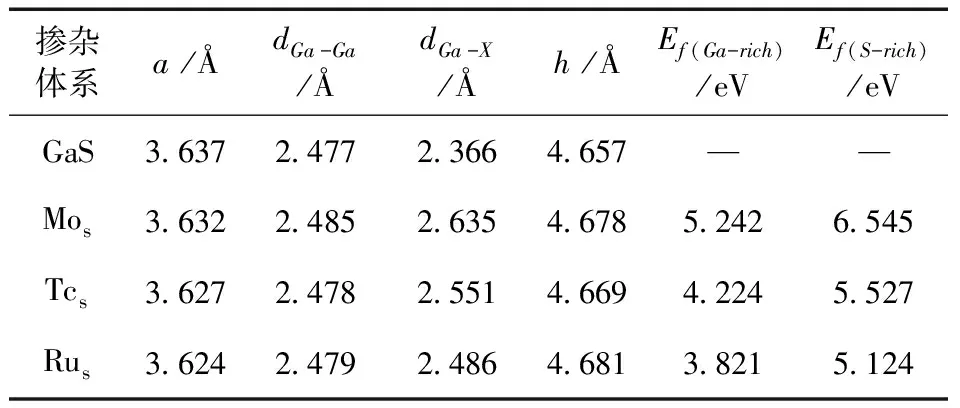
表1 掺杂前后GaS的结构参数及不同条件下的形成能

由表1可知，掺杂体系的dGa-Ga、dGa-X和h结构参数相较于未掺杂体系GaS均有所增大，晶格常数a随着掺杂原子半径(Mo=1.40 Å，Tc=1.35 Å，Ru=1.32 Å)的减小而减小. Ru掺杂体系不论是在Ga-rich还是S-rich条件下形成能都比其余两种掺杂体系小，且所有体系在Ga-rich条件下的形成能都比S-rich条件下的形成能低，说明Ga-rich条件下掺杂体系更容易形成. 但由于两种条件下的形成能均为正值，使得过渡金属原子都很难自发地进入单层GaS材料中，这与Chen等人[16]的研究一致. 为使过渡金属原子自发地进入单层GaS材料中，通常需要附加额外的能量，而外加电场和应变或许是可行路径.

3.2 电子结构

3.2.1能带结构

元素掺杂通常会改变材料的导电性质，而通过能带结构可以直观地了解掺杂前后材料导电性质的变化. 为了分析过渡金属元素X(X=Mo，Tc，Ru)掺杂对单层GaS能带结构的影响，图2给出了掺杂前后不同体系的能带结构. 表2列出了不同体系下的带隙、导电性质及磁性变化情况，其中Eg1代表自旋向上的带隙值，Eg2代表自旋向下的带隙值.

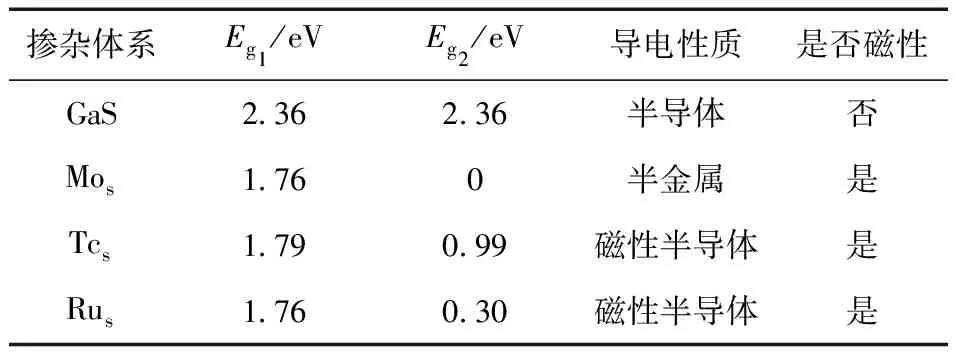
表2 不同掺杂体系的带隙值、导电性质及磁性情况

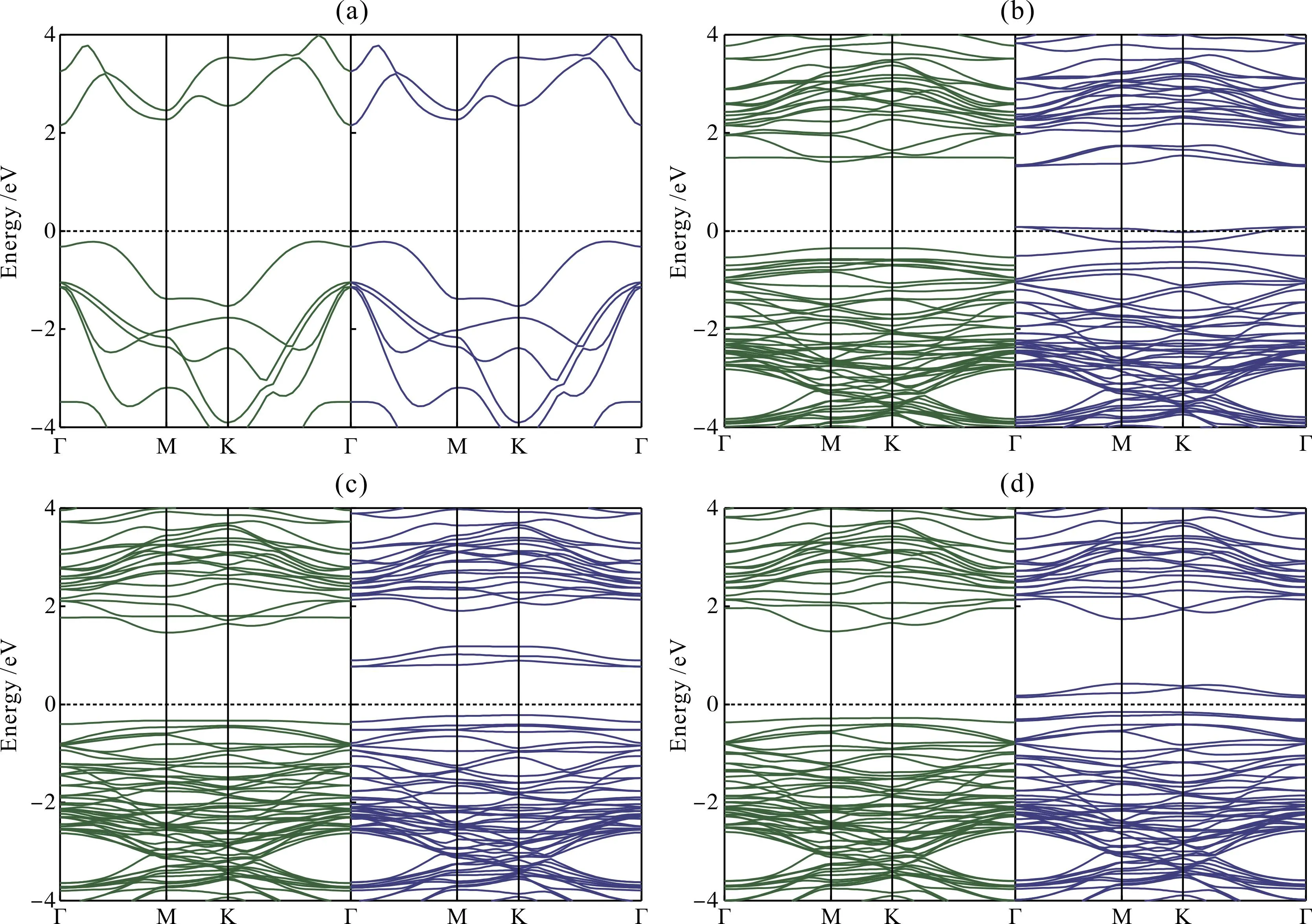
图2 不同掺杂体系的能带结构(绿色代表自旋向上，蓝色代表自旋向下，黑色虚线代表费米能级EF)：(a)未掺杂GaS；(b)Mo掺杂；(c)Tc掺杂；(d)Ru掺杂Fig. 2 Energy band structures of different doped systems (green represents spin-up，blue represents spin-down，and black dotted line represents Fermi energy level EF)：(a)undoped GaS；(b)Mo doped；(c)Tc doped；(d)Ru doped

由图2(a)可知，单层GaS的自旋向上和自旋向下的能带结构完全相同，且导带底和价带顶的位于布里渊区的不同位置处，说明单层GaS是一种非磁性的间接带隙半导体，带隙值为2.36 eV，这与Demirci等人[32]的研究结果吻合. 图2(b)为Mo掺杂体系的能带结构，与未掺杂体系相比自旋向上的带隙值减小到1.76 eV，而自旋向下通道存在穿过费米能级EF的杂质能级，使得掺杂体系呈半金属特性. 因为上下自旋能带结构不同，Mo掺杂体系整体呈半金属铁磁性，说明Mo掺杂后的单层GaS是一种潜在的自旋电子材料. 图2(c)是Tc掺杂体系的能带结构，与Mo掺杂体系相比，其同样具有不对称的能带结构，说明该掺杂体系也具有磁性. 但与之不同的是，Tc掺杂体系自旋向下的能带结构中杂质能级未穿过费米能级EF，两种自旋条件下分别存在1.79 eV和0.99 eV的带隙，该掺杂体系表现出磁性半导体特性. 图2(d)是Ru掺杂体系的能带结构，自旋向上和自旋向下的带隙值分别为1.79 eV和0.30 eV，上下自旋能带结构不对称，且在自旋向下的能带结构中存在4条杂质能级，分别位于费米能级EF两侧，该体系也呈现出磁性半导体特性.

3.2.2态密度

为了进一步分析不同掺杂体系的电子结构，图3给出了掺杂前后各体系的总态密度和主要贡献轨道的分波态密度，其中TDOS(Total Density of States)表示总态密度，黑色虚线表示费米能级EF.

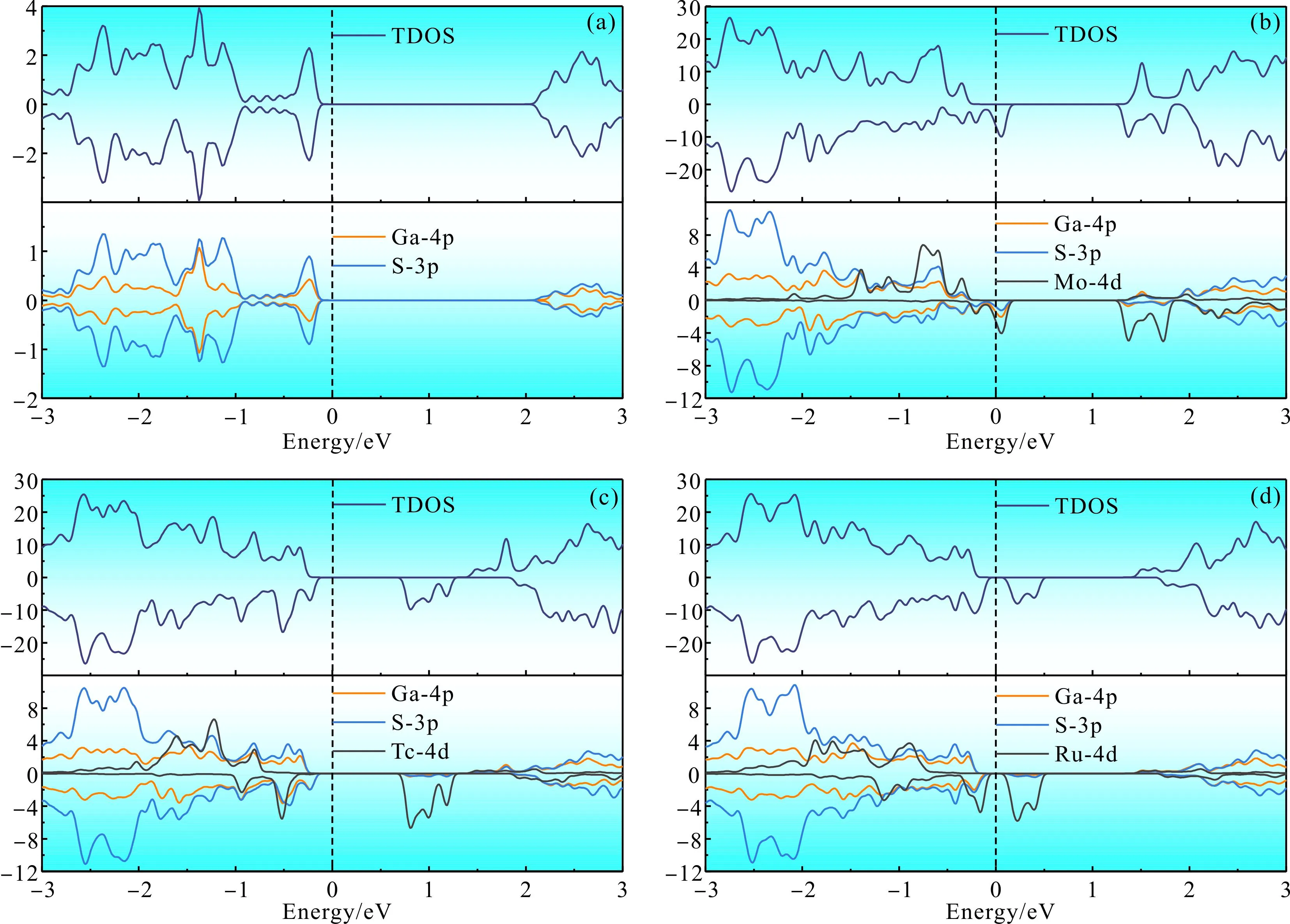
图3 不同掺杂体系的总态密度和分波态密度：(a)未掺杂GaS；(b)Mo掺杂；(c)Tc掺杂；(d)Ru掺杂Fig. 3 Total densities of states and partial densities of states of different doped systems：(a)undoped GaS；(b)Mo doped；(c)Tc doped；(d)Ru doped

由图3(a)可看出，自旋向上和自旋向下的态密度完全对称，说明本征GaS体系不存在磁性，这与能带结构中的分析一致，总态密度主要由Ga的4p轨道和S的3p轨道的电子贡献. 从图3(b)Mo掺杂体系的态密度图可以看出，在费米能级EF和导带底附近均产生了杂质能级，上、下自旋通道发生自旋劈裂，且杂质能级主要由Ga-4p、S-3p和Mo-4d的轨道杂化而成，导带底附近的杂质能级主要由Mo的4d轨道贡献. 图3(c)为Tc掺杂体系的态密度图，自旋向下通道产生了杂质能级，杂质能级主要由Tc的4d轨道贡献，由于杂质能级的出现，Tc掺杂体系的带隙减小到0.99 eV. 图3(d)为Ru掺杂体系，和Tc掺杂体系相比，同样在下自旋通道产生了主要由Ru-4d轨道贡献的杂质能级，杂质能级的出现使得Ru掺杂体系的带隙缩小到0.3 eV，而价带顶主要由Ga-4p、S-3p和Ru-4d轨道共同贡献.

3.3 磁性性质

表3列出了不同掺杂体系的总磁矩和过渡金属X(X=Mo，Tc，Ru)的局域磁矩. 其中，mGa表示与过渡金属原子最近邻Ga原子的局域磁矩，mS表示与过渡金属原子最近邻S原子的局域磁矩，mX表示过渡金属原子的局域磁矩，mtotal表示各掺杂体系的总磁矩.

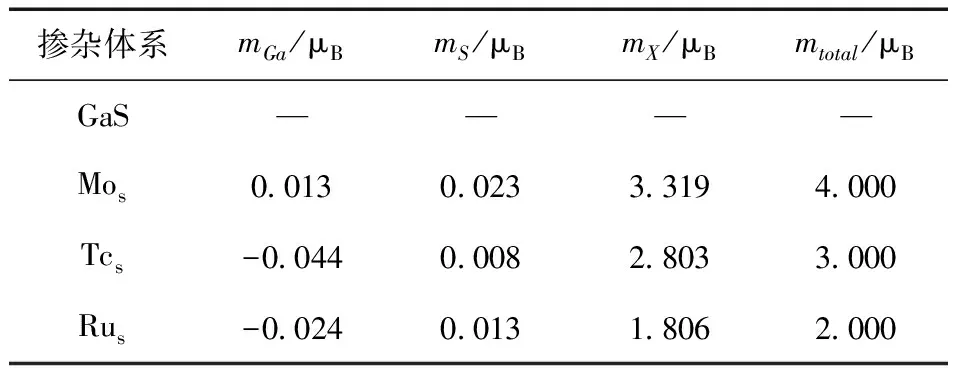
表3 不同掺杂体系的总磁矩和局域磁矩

从表3可知，本征GaS局域磁矩和总磁矩为0，说明本征GaS没有磁性，与之前的能带结构和态密度的结果一致.对于过渡金属元素X(X=Mo，Tc，Ru)掺杂体系来说，分别存在4 μB、3 μB和2 μB的总磁矩，且总体呈减小趋势. 这是由于Mo、Tc和Ru元素的电负性依次增大，过渡金属原子与Ga原子之间的相互作用依次增强，引起过渡金属的价电子更偏向于本征GaS的非磁态，从而导致磁矩的依次减小. 此外，所有掺杂体系的总磁矩均主要由过渡金属原子的局域磁矩贡献，分别为3.319 μB、2.803 μB和1.806 μB.

3.4 光学性质

本文还计算了单层GaS掺杂前后的光学性质变化，DFT方法没有考虑所加真空层的大小对光学性质的影响，而Yang等人[33]提出一种基于介电函数与超胞体积之间的关系来恢复二维材料的固有介电函数和光学性质的计算方法，该方法将真空层的影响考虑到光学性质的计算中，可以预测较为准确的光学性质，但该方法对计算资源的需求较大，所以本文仍采用前者来进行光学性质的定性计算.

3.4.1复介电函数

通常用复介电函数来描述半导体材料的宏观光学响应，其定义如下：

ε(ω)=ε1(ω)+iε2(ω)

(5)

其中，ε1(ω)代表介电函数实部，ε2(ω)代表介电函数虚部，当光子能量为零时的ε1(0)代表材料的静介电常数. 图4(a)为不同掺杂体系复介电函数的实部图，由图可知本征GaS的静介电常数为2.97，掺杂体系的静介电常数分别为7.55、3.37和3.72，掺杂体系的静介电常数都大于本征GaS.在0-2.6 eV范围内，Tc和Ru掺杂体系的实部变大，说明材料的极性增强，对电荷的束缚能力得到提高；而Mo掺杂体系在0.44 eV时存在一个谷值，说明此时的电荷束缚能力较低. 此外，在7.21-9.75 eV范围内实部为负数，表明电磁波在传播时受到衰减. 图4(b)为介电函数的虚部，虚部的值越大，材料对光子的吸收越强，这意味着有更多的电子处于激发态，电子跃迁所需的能量减小. 从图中可以看出，在可见光范围内(1.64-3.19 eV)掺杂体系的虚部比未掺杂体系得到明显提升，光子能量整体往低能区偏移，说明在可见光范围内掺杂体系的光子吸收概率得到提高，处于激发态的电子数目增多.

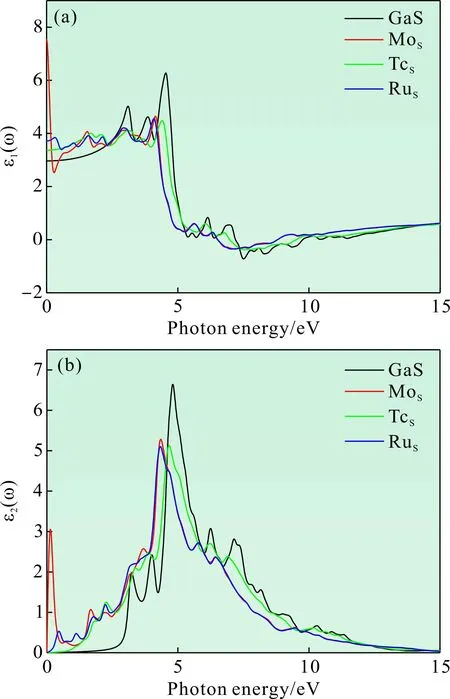
图4 复介电函数的实部和虚部：(a)实部；(b)虚部Fig. 4 Real part and imaginary part of complex dielectric function：(a)Real part；(b)Imaginary part

3.4.2吸收谱和反射谱

图5为过渡金属元素X(X=Mo，Tc，Ru)掺杂前后的吸收光谱和反射光谱，主要体现光在单层GaS材料内部的衰减和表面的反射情况. 其中，图5(a)为掺杂前后不同体系的吸收谱，在可见光范围内(1.64-3.19 eV)，掺杂体系的吸收系数有明显提高.与未掺杂体系相比，掺杂体系均出现红移，这将有利于提高GaS材料在红外光区的光探测能力和对可见光的利用率. 图5(b)是各掺杂体系的反射谱，掺杂体系在低能区的反射系数较本征有所提高，使得单层GaS表面的金属反射性增强. 在低能区，Mo掺杂体系在0.44 eV出现一个谷值，这与复介电函数实部出现谷值的位置相同，说明在该能量下光子不易被反射，且对电荷的束缚能力降低，从而更容易发生能量跃迁.

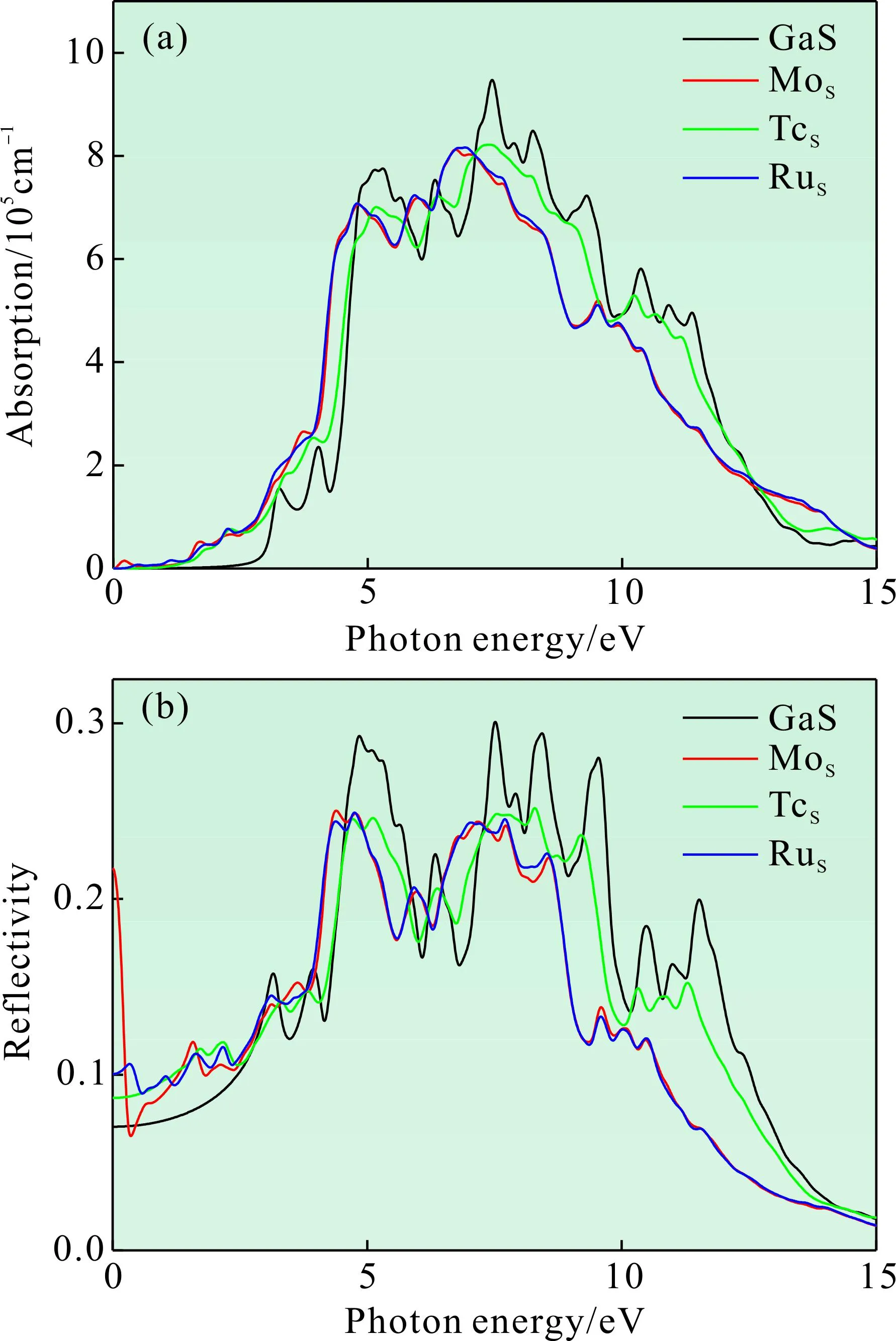
图5 掺杂前后的吸收谱和反射谱：(a)吸收谱；(b)反射谱Fig. 5 The absorption spectra and reflectivity spectra before and after doping：(a)Absorption spectra；(b)Reflectivity spectra

4 结 论

本文基于密度泛函理论对过渡金属元素X(X=Mo，Tc，Ru)掺杂单层GaS的电子结构、磁性性质及光学性质进行了计算. 研究结果表明：掺杂体系在Ga-rich下更稳定，且Ru掺杂体系在Ga-rich条件下的形成能最小，但所有掺杂体系的形成能都是正数，说明过渡金属元素Mo、Tc和Ru不能自发地进入单层GaS体系中.Mo、Tc和Ru掺杂后，上自旋条件下的带隙减小到1.76 eV、1.79 eV和1.76 eV，下自旋条件下的带隙减小到0 eV、0.99 eV和0.3 eV. 在所有掺杂体系中，都引入了杂质能级，其中Mo掺杂体系的杂质能级穿过了费米能级EF，杂质能级主要由过渡金属掺杂原子的4d轨道贡献. 所有掺杂体系中，Mo掺杂体系自旋向上和自旋向下的能带结构分别表现出半导体性和金属性，导致体系呈现出磁矩为4 μB的半金属铁磁性，磁矩主要来源于Mo元素的4d轨道，其特殊的电子结构说明Mo掺杂体系具有在自旋电子学材料领域的应用潜力. Tc和Ru掺杂体系均呈现出磁性半导体特性，各自的总磁矩分别为3 μB和2 μB，磁矩的主要来源仍为Tc和Ru元素的4d轨道，这为单层GaS材料在磁性半导体领域的应用提供了可能. 此外，掺杂后单层GaS的静介电常数得到提高，增强了对电荷的束缚能力. 所有掺杂体系在可见光区的吸收系数增大，吸收谱出现红移，使单层GaS对可见光的利用率增加，在近红外区具有作为光探测器材料的应用潜力.