二维6H-SiC光学特性的应变调控
2024-02-01薛丽丽司志泽王卓群王衍营
薛丽丽, 高 静, 司志泽, 王卓群, 王衍营, 张 雨
(1.山东省产品质量检验研究院, 济南 250100; 2. 青岛科技大学 化学与分子工程学院, 青岛 266045)
1 引 言
近年来,以石墨烯为代表的二维材料由于具有优良的物理化学性质在光电子器件、纳米技术领域有着广泛的应用[1,2]. 除了石墨烯,科学家还合成了过渡金属硫化物[3]、硼烯[3]、硅烯[4]、磷烯[5]、锗烯[6]等二维材料. 相比于三维体相材料,二维材料具有比表面积大,密度小等优势,在半导体器件、航空航天、化学化工等领域得到广泛的应用. 常见的硅烯是二维g-SiC,属于第三代化合物半导体,相比于Si、Ge半导体,其带隙是Si的3倍,电子迁移速率是Si的2.5倍,且易与氧气反应生成SiO2薄膜,能够防止基体进一步氧化,是制作5G高频通信器件的理想材料[7]. 同时由于电子迁移率高、化学性质稳定、具有较高的催化活性等优点,常被用于制作光催化剂[8]. 但是二维g-SiC在光催化方面存在一些问题,其中一点就是带隙较宽(2.58 eV)[9],而可见光范围为1.6 eV~3.2 eV,所以二维g-SiC只对部分可见光有响应,因此减小带隙,提高对可见光的吸收效率是二维g-SiC必须要解决的一个问题.
目前能够有效调节能带的方法包括掺杂[10]、堆垛[11]、吸附[12]、异质结[5]等等,但是这些方法都属于化学方法,需要通过分子束外延(MBE)、化学气相沉积(CVD)等来实现,工艺复杂. 近年来,科学家发现,通过形变就能够对材料的能带产生作用,进而得到理想的物理性质[13]. 目前通过应变改变材料的光电性质已经形成了新的研究方向—应变光子学. 基于应变光子学的原理,理论和实验室都有深入的研究,如Liu等人[14]通过第一性原理计算发现压缩应变能提高二维AlP3对可见光的吸收,提高载流子迁移率;Ghorbani等人[15]研究发现应变能提高过渡金属硫化物的导电性,Liu等人[16,17]研究发现应变能提高BP/β-AsP、MoSSe/g-SiC范德瓦尔斯异质结光催化制氢的效率. 实验上二维g-SiC常与Si[18]、石墨烯[19]、AlN[20]、MgO[21]形成异质结,但是由于晶格存在2%~5%的错配度,这就导致了晶格产生应变,另外二维g-SiC晶体生长过程中也产生大量的晶界,这些晶界同样存在应力集中的问题,导致晶格畸变. 总体分析,二维g-SiC始终处于晶格被压缩或拉伸的环境中,这必然影响晶体的能带结构. 虽然应变调控二维过渡金属硫化物的能带结构已经有了广泛的研究,但是关于应变对g-SiC能带结构、光学性质、光催化性质影响的研究目前还未见报道,基于此,本文将利用基于密度泛函理论的第一性原理研究应变对g-SiC能带结构、光学性质、光催化性质的调控机制.
2 计算方法与模型
2.1 计算方法
第一性原理是在原子、电子层面研究物质物理化学性质的有效方法之一[22-23],本研究采用基于密度泛函理论(DFT)的第一性原理研究应变对g-SiC的能带结构以及光学性质的影响. 晶格优化采用的是广义梯度近似(GGA)中的PBE泛函[24],价电子选取的是C:2s22p2、Si:3s23p2,处理价电子相互作用选取的是超软赝势(Ultrasoft Pseudopotential)[25],在收敛性测试中,截断能选取的是550 eV,布里渊区Monkhorst-Pack网格选取的是12×12×6. 收敛标准是SCF=2×10-6eV/atom,总能量Etotal<2×10-5eV/atom,原子作用能Eatom<0.05 eV/atom,最大位移Dmax<0.002 Å. 由于密度泛函理论计算能带比实验得到的小,所以在计算能带结构和光学性质时采用的是HSE06泛函.
2.2 模 型
二维g-SiC具有蜂巢状的石墨烯结构,Si-C原子比为1∶1(一个Si原子连接3个C原子,化学键是sp2杂化轨道),最常见的g-SiC是6H-SiC(结构模型如图1所示),属于六方晶系,空间群是P63mc,原子在空间按照ABCBAC的顺序排列,每六层原子一个周期. 通过GGA-PBE优化后的晶格常数为a=3.024 Å,实验上测得的a=2.921 Å[9],HSE06计算得到的带隙宽度Eg=2.61 eV,实验上测得的为2.58 eV[9],Tang[5]通过第一性原理计算得到的为2.54 eV,所以选取的计算方法满足了精度要求. 计算模型采用了2×2×1的超晶胞,模型中含有24个Si和24个C.
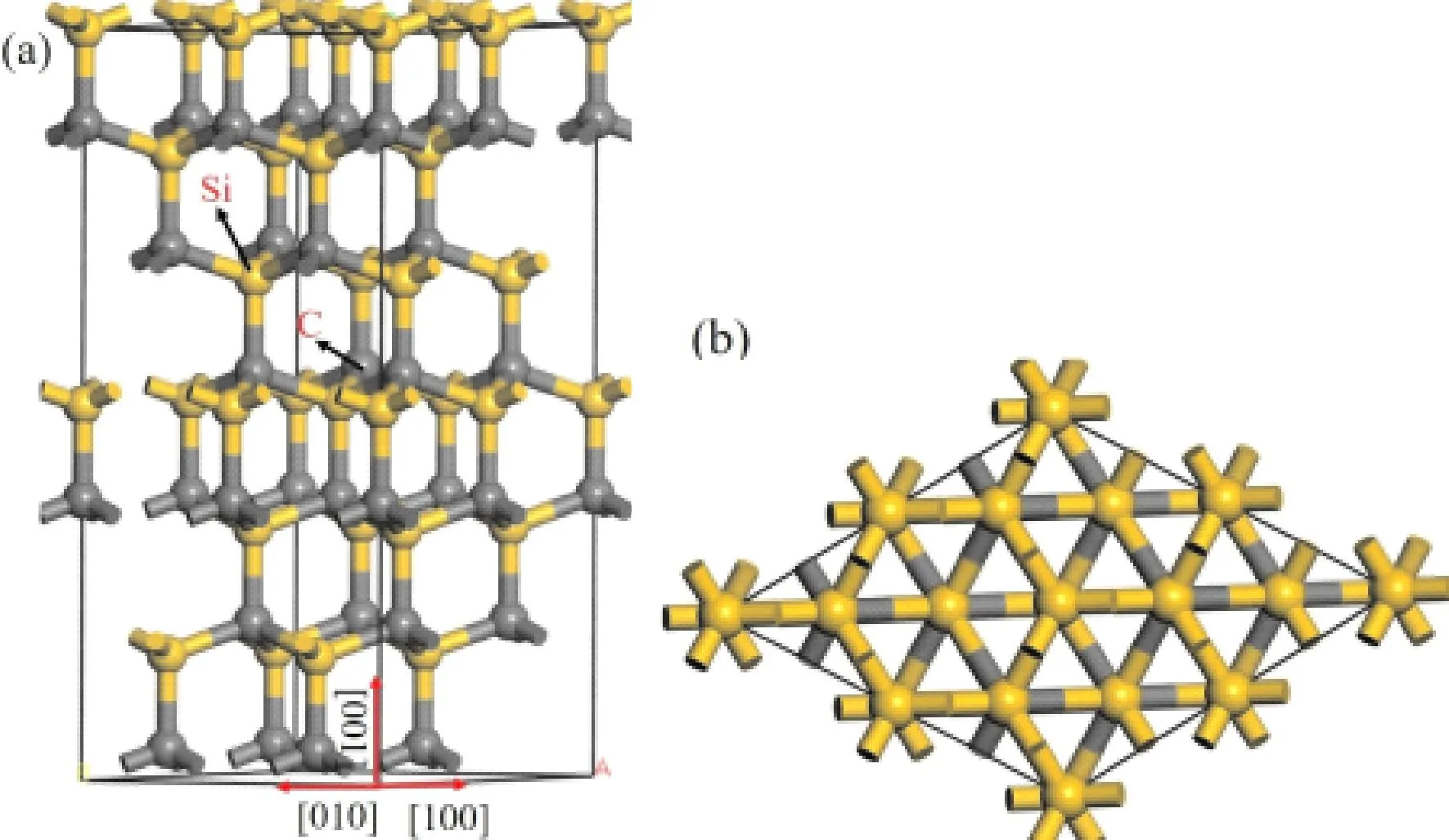
图1 6H-SiC模型:(a)侧视图;(b)俯视图Fig. 1 6H-SiC model:(a)side view;(b)top view
3 结果与讨论
3.1 能带与态密度
由于6H-SiC与其他晶体形成异质结时的晶格错配度在2%~5%,所以以-6%、-4%、-2%三个压缩应变和2%、4%、6%三个拉伸应变为研究内容. 图2(a)是拉伸应变对能带的影响,可以看出6H-SiC属于间接带隙半导体,且应变没有改变半导体的类型,6H-SiC在没有施加应变、以及应变在2%、4%、6%对应的导带底(CBM)分别为2.61 eV、2.39 eV、2.37 eV、2.2 eV,而整个过程中价带顶没有发生变化,都位于G点的费米能级上,所以施加拉伸应变减小了带隙宽度. 图2(b)是压缩应变对能带的影响,应变在-2%、-4%、-6%对应的CBM分别为2.54 eV、2.43 eV、2.31 eV,带隙也是逐渐减小的.
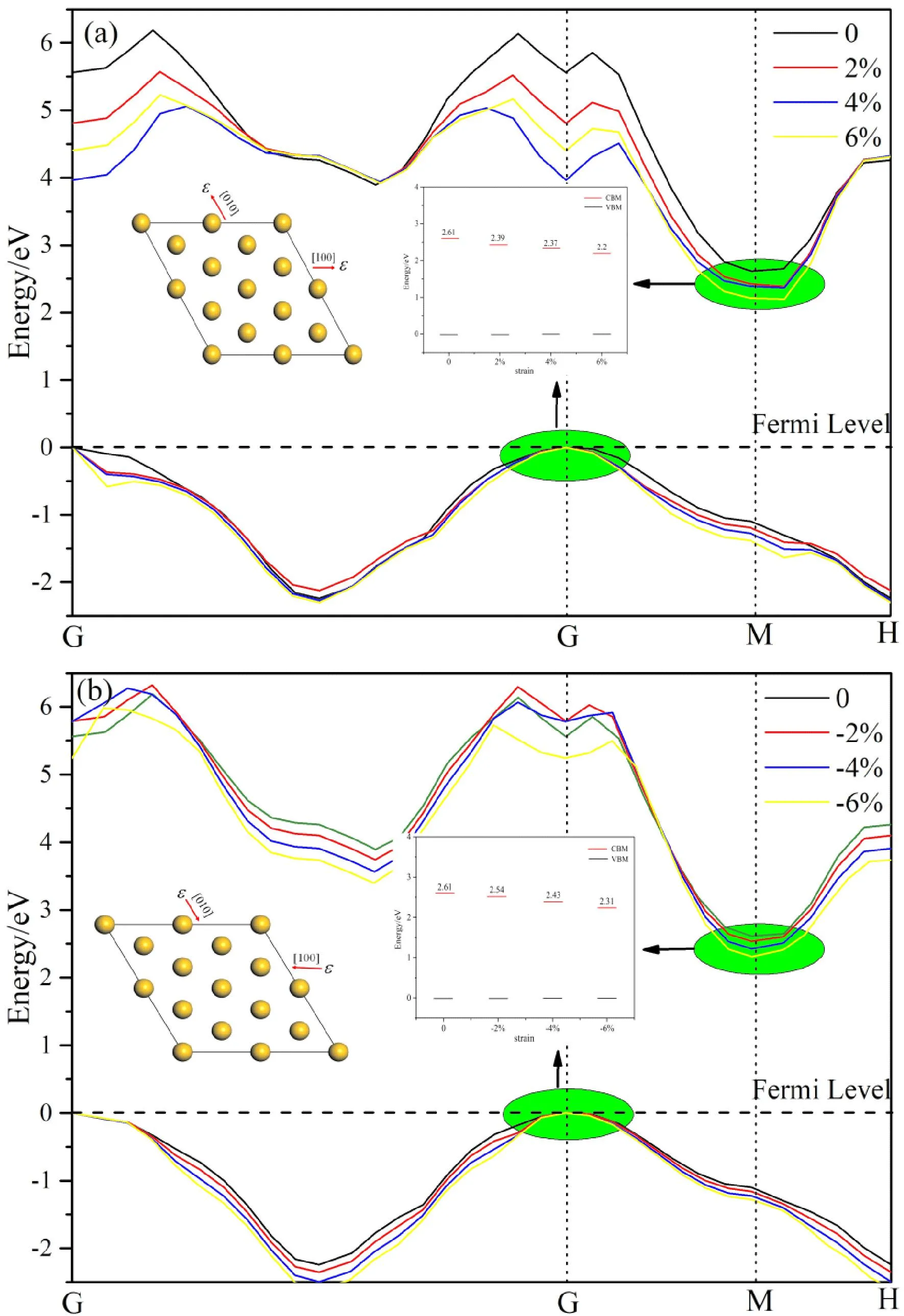
图2 应变对6H-SiC能带结构的影响:(a)拉伸应变;(b)压缩应变Fig. 2 Effects of strain on band structure of 6H-SiC :(a)tensile strain;(b)compressive strain
为了从电子层面上解释带隙变化的原因,图3给出了应变对于态密度的影响. 图3(a)是无应变时对应的6H-SiC态密度图,可以看出导带底部主要由Si的3p态、C的3p态组成,同时含有少量的Si的3s态、C的3s态;价带顶主要由Si的3p态、C的3p态组成,在-5.5 eV~-8.6 eV之间含义少量的Si的3s态,在6.3 eV处Si的3p态与C的3p态杂化作用明显,形成明显的杂化峰,在价带中的-1.9 eV处,Si的3p态与C的3p态杂化形成了杂化峰,峰的存在为电子的跃迁提供了平台. 图3(b)是6%的拉伸应变对应的态密度,可以看出Si的3p态向低能级方向延展,从能带图上也能看出导带底向下侧延展,相比没有应变下导带更为稀疏,而价带基本没有变化,所以带隙减小. 另外在6.2 eV附近的杂化作用减弱,能谷变宽,向下挤压导带底,也导致了带隙减小. 在-2.5 eV、-3.5 eV处,Si的3p态与C的3p态杂化形成两个新的杂化峰,有利于电子跃迁. 图3(c)是-6%的压缩应变对应的态密度,和图3(a)相比,导带中4.5 eV处的杂化峰变宽,向低能级方向挤压导带底,导致带隙变窄. 另外价带顶的态密度峰值明显变宽,有利于电子跃迁.
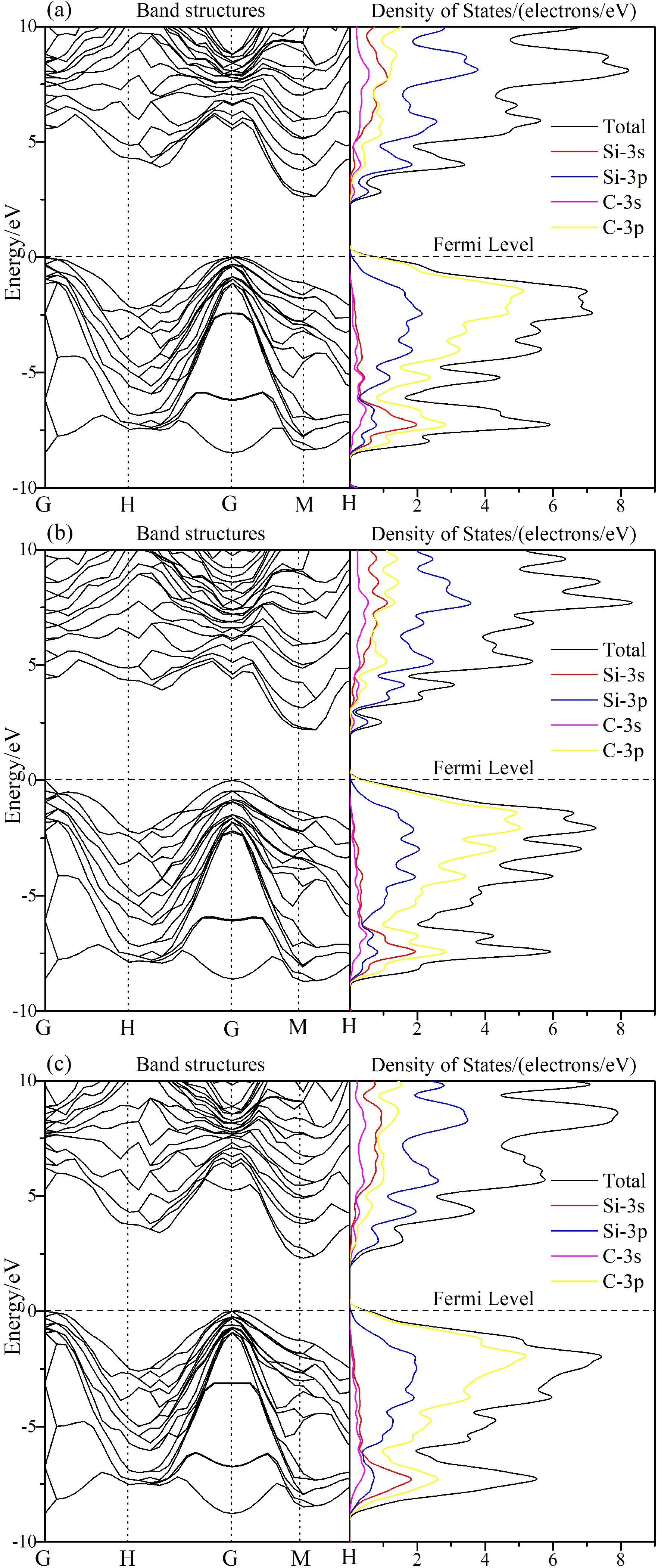
图3 应变对6H-SiC态密度的影响:(a)无应变;(b)拉伸应变6%;(c)压缩应变-6%Fig. 3 Effects of strain on the density of 6H-SiC states :(a)no strain;(b)tensile strain 6%;(c)compressive strain -6%
3.2 吸收系数
光学吸收系数能够反应材料对光的响应情况,光学吸收系数α可由方程(1)得到[26],其中ε1(ω)、ε2(ω)分别是复介电函数的实部和虚部,虚部ε2(ω)和光的吸收有关,ε1(ω)可以由ε2(ω)推导出,称为克喇末-克勒尼希关系式(Kramers-Kronig色散关系). 式中ω是光的圆频率,BZ是第一布里渊区,EC、EV分别是导带底和价带顶,MCV(k)是动量矩阵元,s是A辅助电磁量的单位矢量. 图4(a)是拉伸应变对6H-SiC光学吸收系数的影响,可以看出没有应变的情况下6H-SiC的吸收限在2.5 eV左右,与计算得到的带隙宽度非常吻合,随着应变的增加,吸收曲线向低能级方向移动,即发生红移,这也与带隙宽度的变化方向一致. 在可见光区(1.6 eV~3.2 eV)应变导致了6H-SiC有了明显的吸收. 另外无应变以及6%的拉伸应变吸收曲线的最高峰分别位于7.5 eV和6.5 eV处,对应于图3(a、b)中价带顶部最高峰向导带底部最高峰的跃迁,在4.5 eV~5.5 eV区间存在若干个小的吸收峰,主要是由于导带中最高峰与带隙之间存在若干个小的杂化峰导致的. 图4(b)是压缩应变对6H-SiC光学吸收系数的影响,和拉伸应变的变化规律非常相似:随着应变的增加,吸收曲线向低能级方向移动,即发生红移,这也与带隙宽度的变化方向一致. -6%的压缩应变吸收曲线的最高峰位于6.2 eV处,对应于图3c中价带顶部最高峰向导带底部最高峰的跃迁.
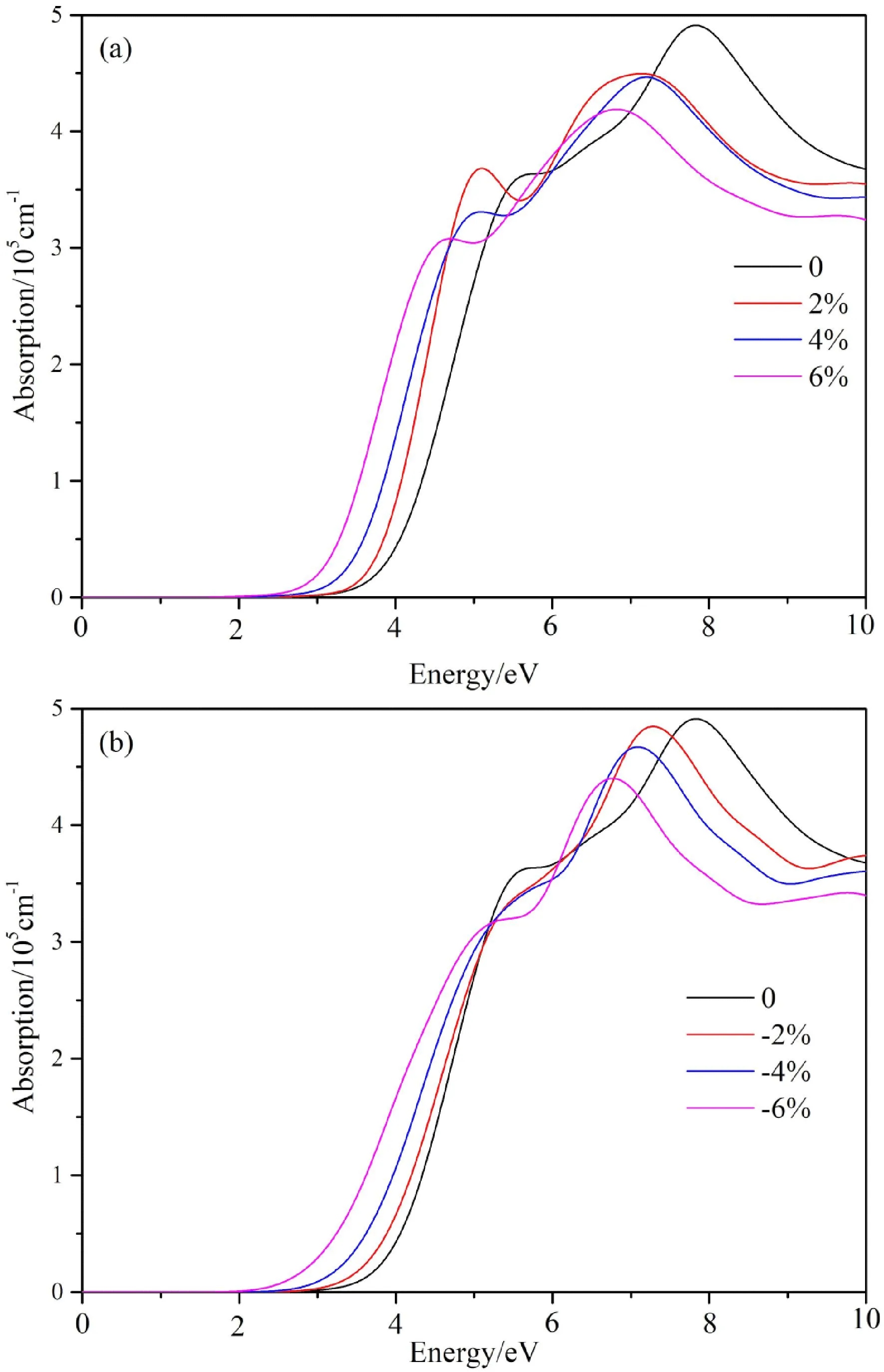
图4 应变对6H-SiC光学吸收系数的影响:(a)拉伸应变;(b)压缩应变Fig. 4 Effects of strain on optical absorption coefficient of 6H-SiC :(a)tensile strain;(b)compressive strain
(1)
(2)
δ[ECk-EVk-ħω]d3k
(3)
3.3 载流子迁移率
载流子迁移率与电子-空穴的分离状态有关,迁移率越高意味着电子-空穴越容易分离[27]. 载流子的迁移率可由方程(4)得到[28],其中方程(5)是弹性模量C,方程(6)是有效质量m*的计算方程,方程(7)是形变能Ed的计算公式.
(4)
(5)
(6)
(7)
经计算6H-SiC的C=214 GPa,电子的形变能Ede=3.85 eV,空穴的形变能Edh=2.12 eV. 表1是计算得到的应变对6H-SiC载流子迁移率的影响,从表中可以看出,没有施加应变的情况下空穴和电子的载流子迁移率分别为0.12×104cm2/V·s和0.53×103cm2/V·s,空穴的载流子迁移率是电子的两倍,施加拉伸应变后空穴的载流子迁移率最高达0.162×104cm2/V·s,电子的最高达0.604×103cm2/V·s,所以拉伸能够提高载流子迁移率,有利于载流子产生移动,而在拉伸应变下,空穴的载流子迁移率是电子的2.5倍,有利于空穴和电子的有效分离. 压缩应变也有类似的规律,施加压缩应变后空穴和电子的载流子迁移率都有明显提高.

表1 应变对6H-SiC载流子迁移率的影响
3.4 光催化分解水

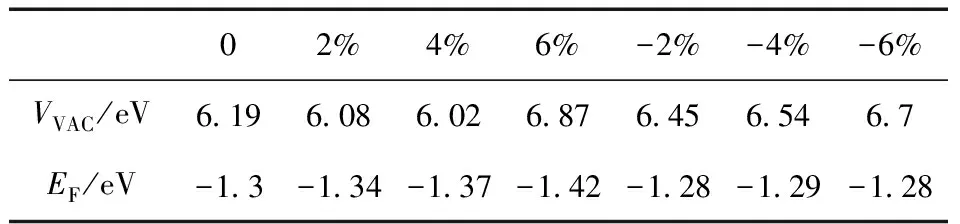
表2 应变对6H-SiC真空静电势和费米能级的影响
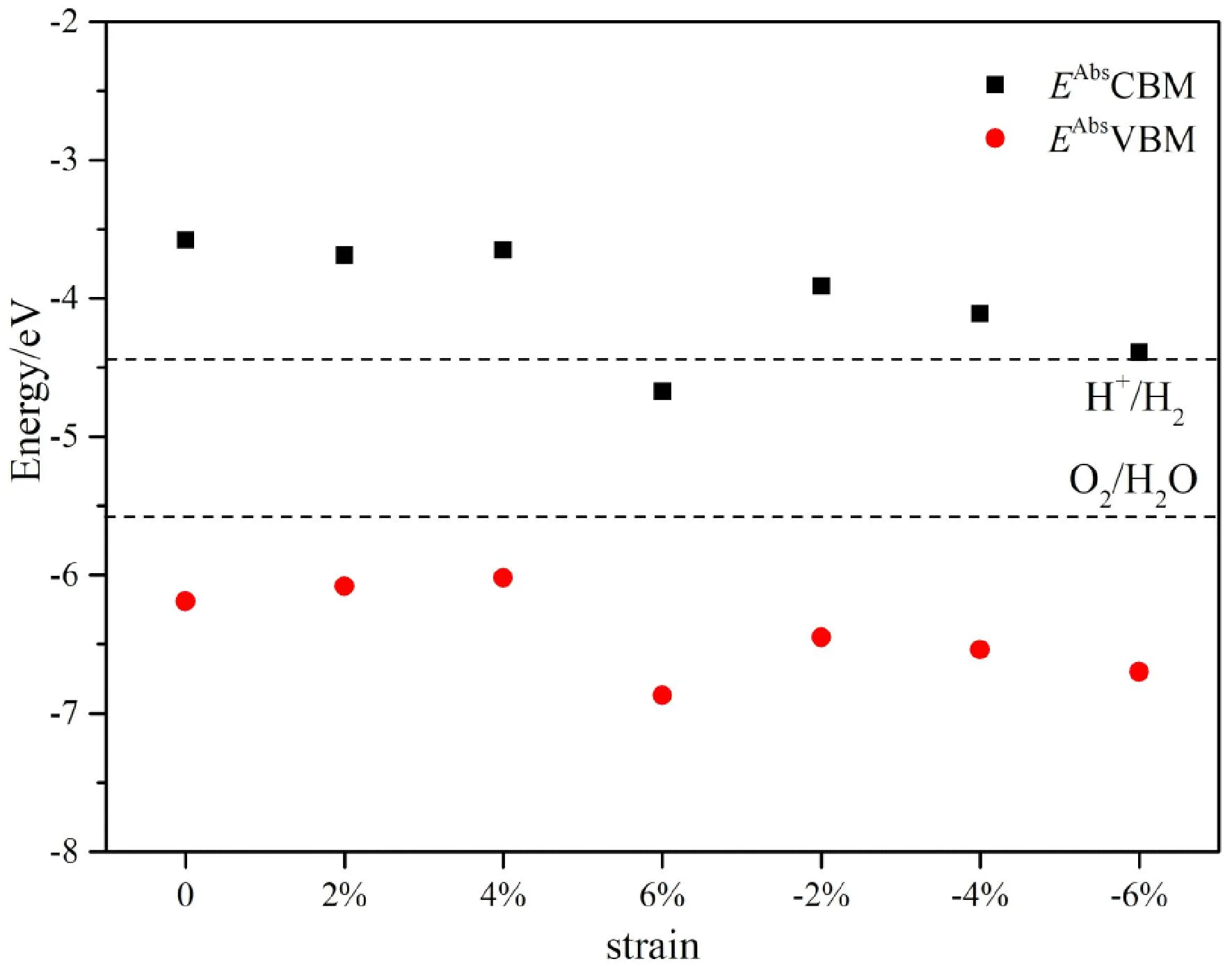
图5 应变对6H-SiC带边的影响Fig. 5 Effects of strain on band edge of 6H-SiC
(8)
Φ=VVAC-EF
(9)
4 结 论
采用基于密度泛函理论的GGA-PBE方法对6H-SiC进行了几何结构优化、采用HSE06对能带、态密度、光学性质进行计算得到了以下几个方面的结论:
(1)6H-SiC在施加应变后导带底降低,价带顶不变,导致带隙减小.
(2)随着应变的增加,吸收曲线向低能级方向移动,即发生红移,与带隙宽度的变化方向一致,有利于可见光的吸收.
(3)施加应变后空穴的载流子迁移率提高,有利于载流子移动,且空穴的载流子迁移率是电子的2.5倍,有利于空穴和电子的分离.
(4)综合应变对带隙大小、带边位置的影响可知,应变在±2%、±4%时对可见光的吸收以及光催化分解水最有效.
