CuO掺杂C3N对C5F10O分解组分吸附性能的第一性原理研究

王成江, 项思雅, 武俊红, 王凌威, 王海涛, 万思宇

(三峡大学 电气与新能源学院, 宜昌 443002)

1 引 言

近年来，碳氟类环保型绝缘介质全氟五碳酮(C5F10O)作为极有可能替代SF6的气体之一，引起了国内外学者的广泛关注. C5F10O气体无毒、不易燃，能够稳定安全的应用于工程中，其介电强度是SF6气体的两倍，而全球变暖潜能值仅为1[1]. 早在2015年，ABB公司就生产出以C5F10O混合气体为绝缘介质的开关柜，并在苏黎世的一个变电站投入运行[2]. 在实际工程应用中，气体绝缘设备内不可避免地会出现一些绝缘缺陷，这些缺陷可能引发不同形式和严重程度的局部放电或局部过热等绝缘性故障[3]. 伴随故障产生的局部强电磁能及局部高温，会使C5F10O气体发生分解，产生的各类自由基与设备或空气中含有的微量的水反应，最终生成CF4、C2F6等碳氟化合物以及剧毒物质CF2O和HF[4，5]. 这些放电分解物质的存在会极大影响C5F10O绝缘介质的电负性能，另外有毒产物的不断堆积不仅会污染大气环境，还会为绝缘设备以及工作人员的人身安全带来威胁. 在绝缘设备内部放置吸附材料是解决此问题的主要方法. 在实际使用时要求吸附材料对放电分解组分具有较高的选择吸附性，从而在不妨碍气敏传感器正常检测的情况下，实现对特定气体的清除[6].

Yang等[7]通过2，3-二氨基吩嗪聚合形成一种新型类石墨烯二维材料C3N. 氮原子的加入使得本征的C3N表现出高于石墨烯的化学活性与载流子迁移率，但在结构稳定性上仍保持了与石墨烯相同的水平[8]，这使得C3N在吸附领域具有较大的应用潜力. 目前的研究表明本征C3N对NO2、SO2等有毒气体的吸附能力不够强[9]，而经过Pd掺杂后的C3N对NO、NO2和SO2都产生了较强的化学吸附[10]. 通过对本征C3N进行掺杂改性可以实现对更多气体的强吸附[11]. CuO是一种常见的p型金属氧化物，随着研究的深入，学者们发现CuO具有较高的催化活性，能促进表面化学反应的进行，因此其可作为掺杂物改善基底材料的性能[12]. 类似过渡金属氧化物掺杂C3N对特定气体产生了吸附[13]也为CuO-C3N吸附C5F10O放电分解组分的研究提供了坚实的理论支撑.

目前对于改性C3N材料的研究主要集中在吸附如H2、NO等常见气体以及SF6分解组分上，鲜有关于其对新型环保绝缘气体C5F10O放电分解组分吸附性能的报道. 本文选定CF4、C2F6两种最主要的碳氟类分解组分以及有毒分解产物CF2O、HF为被吸附对象，基于第一性原理模拟计算了这四种典型的C5F10O分解组分与CuO分子掺杂C3N材料之间的吸附过程，通过对吸附能、态密度、恢复时间、电荷转移量与差分电荷密度这些参数的分析，可以从理论层面详细了解气体与材料表面之间的相互作用情况，从而判断CuO-C3N是否可以实现对C5F10O分解组分的选择性吸附. 本文的研究结果为研发针对C5F10O废气处理的高性能吸附材料提供了理论依据.

2 计算方法与仿真模型

本文的所有仿真计算都是在Materials Studio软件里的Dmol3模块中实现的. 在处理表面问题时，广义梯度近似(Generalized Gradient Approximation，GGA)的计算精度比局域密度近似(Local-density Approximation，LDA)高，所以本次计算将采用GGA方法，并选用Perdew-Burke-Ernzehof(PBE)泛函处理电子间的交换关联作用[14]. 另外选择p极化双数值轨道基组(Double Numerical Polarization，DNP)作为原子轨道计算的基组函数. 原子几何优化能量收敛设为1×10-5Ha，原子力收敛标准设为0.002 Ha/Å，原子的最大位移设置为0.005 Å，自洽场SCF的收敛标准设置为1×10-6Ha[15]. 选定布里渊区为6×6×1的Monkhorst-Pack k点网格.

首先构建了2×2×1的本征C3N单层超晶胞模型，共含有24个C原子及8个N原子，真空层厚度设置为1.5 nm以避免相邻分子层之间的相互作用. C3N表面共有六种掺杂位，分别为C原子及N原子正上方的T配位、碳环及C/N环的中空H配位、C-C键及C-N键的B桥配位，如图1所示. 其次还建立了CF4、C2F6、CF2O、HF四种气体分子优化后的模型，见图2.

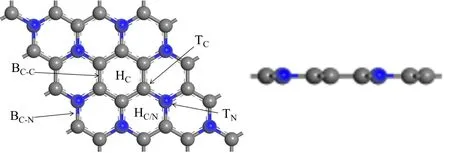
图1 本征C3N优化模型Fig.1 Optimization model of intrinsic C3N

图2 气体分子优化模型Fig.2 Optimization models of gas molecules

将优化后的CuO分子以平行、Cu原子朝下与O原子朝下三种方式置于C3N表面的六种掺杂位上，可以得到共18种初始吸附构型. 通过比较不同初始吸附构型的形成能，可以最终确定CuO掺杂C3N的最稳定模型，形成能Eform的公式如下[16]：

Eform=Edopant-surf-Edopant-ESurf

(1)

其中Edopant-surf为CuO掺杂C3N基底后的能量，Edopant和Esurf分别为掺杂材料CuO分子和C3N基底的能量.Eform的绝对值越大，CuO与C3N之间的结合就越稳定. 当CuO分子以平行的方式置于C3N表面时，随着仿真的进行，最终CuO将从平行状态变为Cu原子朝下的状态. 因此为了简化计算过程，本文只考虑O原子朝下与Cu原子朝下两种方式，共12种初始吸附构型. 根据公式计算得到12种初始吸附构型下形成能的绝对值，如图3所示.

图3 不同初始吸附构型下的|Eform|Fig. 3 |Eform| under different initial adsorption configurations

比较图3中的形成能，发现当CuO分子以O原子垂直向下的方式位于TC配位时，|Eform|达到最大值1. 728 eV，为CuO-C3N的最稳定掺杂结构，如图4所示.

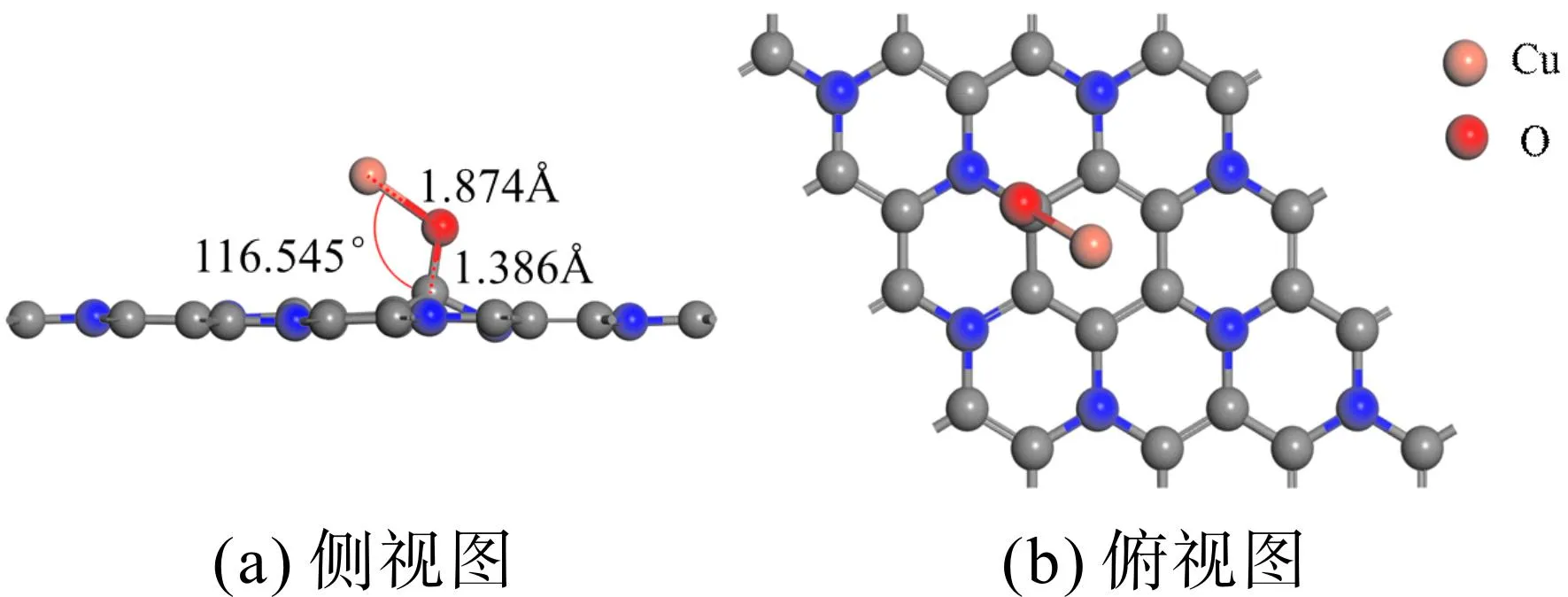
图4 CuO掺杂C3N结构Fig. 4 Structure of CuO-doped C3N

3 吸附性能分析

3.1 吸附能与吸附结构

吸附能与吸附结构可以较为直观地反映出气体分子与材料表面相互作用的强弱，吸附能Eads的公式定义为：

Eads=Egas+Surf-Egas-ESurf

(2)

其中Egas+Surf为吸附表面吸附单个气体分子后稳定体系的总能量；Egas为单个气体分子的能量；ESurf为吸附表面的能量.Eads为负值表明吸附过程是自发进行并伴随着能量的释放，吸附能的绝对值越大表明吸附表面与气体分子间相互作用越强，吸附结构越稳定[17].

将优化后的气体分子以不同的角度靠近CuO-C3N表面，以CF4为例，考虑了C垂直于Cu、O原子以及F垂直于Cu、O原子四种吸附方式. 通过比较不同吸附方式下的Eads，最终确定了CF4、C2F6、CF2O、HF分子在CuO-C3N上的最稳定吸附结构. 另外，为了研究CuO掺杂前后C3N体系吸附气体分子能力的变化，此处还对本征C3N吸附四种典型C5F10O分解气体时的吸附能进行了计算，对于每种气体分子，都考虑了如图1所示的六个吸附位点来获得其最稳定吸附结构. 四种气体分子吸附于本征C3N及CuO-C3N的最稳定结构如图5所示.

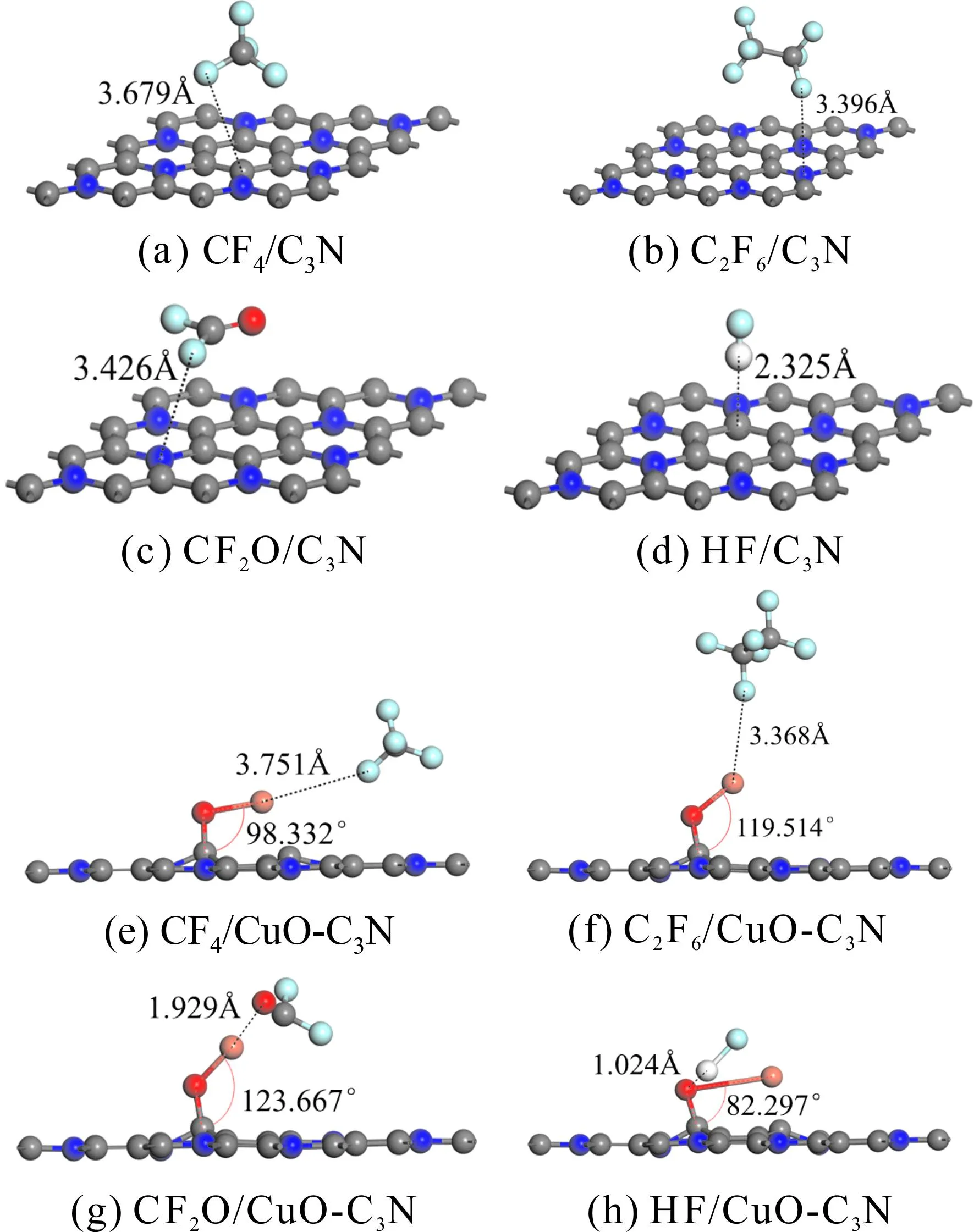
图5 气体分子最稳定吸附结构Fig.5 The most stable adsorption structures of gas molecules

根据吸附能公式及图5中的最稳定吸附结构，可以得到如表1所示的详细的吸附参数.从表1给出的吸附能可以看出，这四种气体的吸附反应都是可以自发进行的放热反应，但本征C3N与这四种气体之间的相互作用都非常弱，吸附能皆低于0.2 eV，属于物理吸附的范畴，说明本征C3N对C5F10O分解气体的吸附较弱，极不稳定. 观察图5a～5d，不难发现吸附后的气体分子与C3N表面几乎没有发生任何变化，两者之间的吸附距离较远，均超过了2 Å. 从原子键长分析，CF4、C2F6及CF2O分子相应的键长变化在0～0.002 Å范围内，HF分子的H—F较吸附前增长了0.008 Å，键长均无明显的增大或减小. 这些结果都说明C5F10O分解气体无法稳定吸附于本征C3N表面.

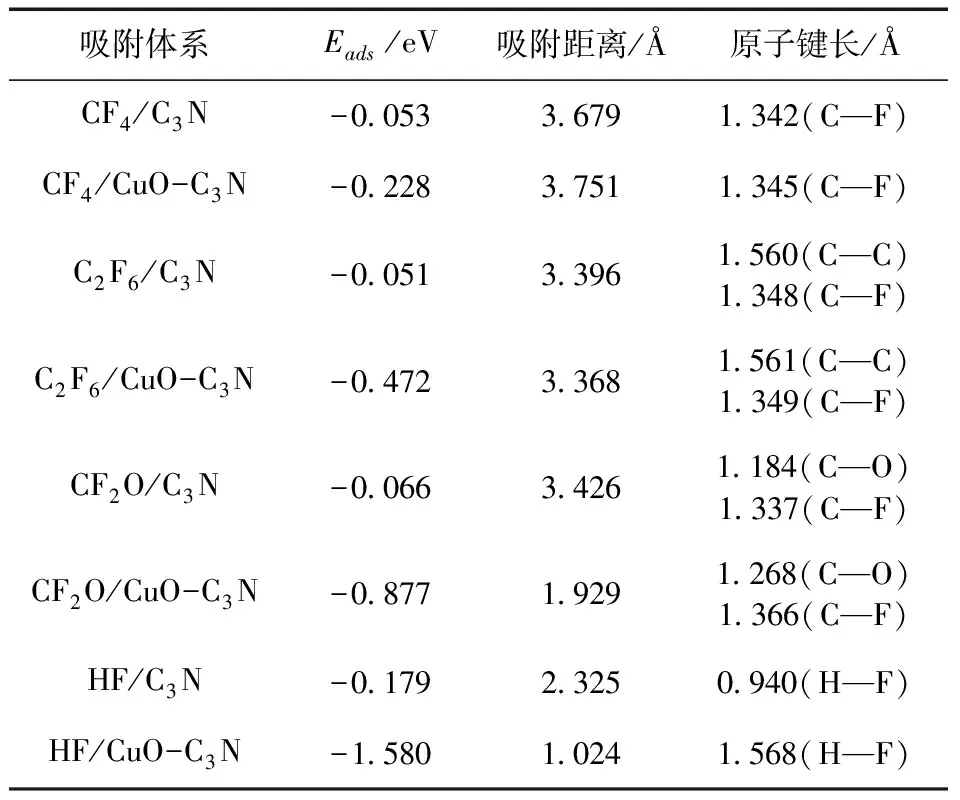
表1 吸附参数

观察图5e～5h所示的CuO-C3N吸附体系，发现CF4和C2F6与吸附表面的距离较远，气体分子与CuO分子的键长和角度只是略微改变；CF2O与CuO-C3N表面的距离从未掺杂时的3.426 Å减小至1.929 Å，C—O、C—F键分别被拉长约0.084 Å和0.229 Å；吸附后的HF与表面仅相距1.024 Å，H—F键增长了约0.6 Å，Cu—O甚至从原来的1.874 Å被拉长至3.097 Å，合理推断HF与CuO分子在吸附过程中可能发生断键的情况. 通过表1给出的吸附参数可知，CF4、C2F6、CF2O及HF分子在CuO-C3N表面的吸附能较在本征C3N有极大提高.

综合上述分析，CuO掺杂C3N材料对C5F10O四种分解气体的吸附效果都要强于本征C3N，其对这四种气体的吸附强度从大到小依次为HF>CF2O>C2F6>CF4. 初步判断HF与CF2O可以稳定吸附于CuO-C3N，使得CuO-C3N具备了从C5F10O分解后的混合气体中选择性吸附HF与CF2O的能力.

3.2 态密度

通过分析态密度可以进一步研究基底材料与气体分子之间的相互作用机制，判断两者是否发生较强烈的化学相互作用，明确气体在材料表面的成键情况.

图6为CF4、C2F6吸附体系中相互靠近的Cu原子与F原子的局部态密度(PDOS)图. 观察图发现，CF4和C2F6的F 2p轨道并没有与Cu原子的任一电子轨道发生重叠现象，说明CuO-C3N与CF4、C2F6之间没有发生化学相互作用，CuO-C3N无法稳定吸附这两种气体分子.

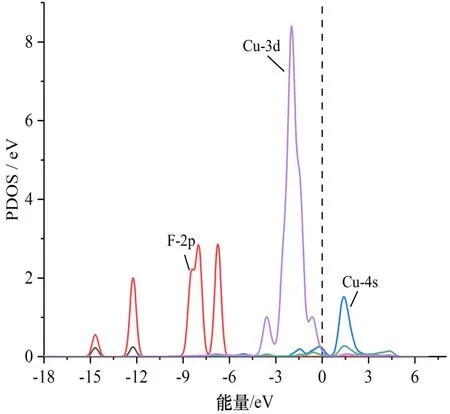
(a)CF4的F原子与CuO的Cu原子PDOS

图7a为CF2O吸附CuO-C3N后相互靠近的原子的PDOS图. 从Cu原子与C、O原子的局部态密度图可以看出，Cu 4s轨道没有与C、O原子的任何轨道发生重叠，Cu 3d轨道在-6 eV及费米能级附近与O 2p轨道同时出现态密度峰，因此Cu与O之间极有可能形成化学键. C原子的2s、2p轨道在0 eV附近与Cu 3d轨道产生杂化，说明Cu—C键也有很大概率存在. 图7b、c是HF吸附体系的PDOS图，图7b中的H 1s轨道在-9.5 eV处与O 2p轨道发生重叠杂化，且H 1s与O 2s、O 2p在-5.0 eV处均同时出现态密度峰. 图7c中的F 2p轨道与Cu 3d轨道在接近费米能级的-5～0 eV能量域中的多个能级上形成了重叠，说明HF与CuO-C3N之间发生了强烈的化学反应. H、O原子以及F、Cu原子的电子轨道在多处出现杂化重叠，使得H-O键和F-Cu键的形成变得更加有说服力. 另外，比较H原子与F原子的电子轨道后发现H 1s与F 2s、2p没有态密度峰的重叠，说明H-F键很有可能已经断裂. 且对比图7a发现HF吸附体系中的原子轨道重叠程度要高于CF2O吸附体系.

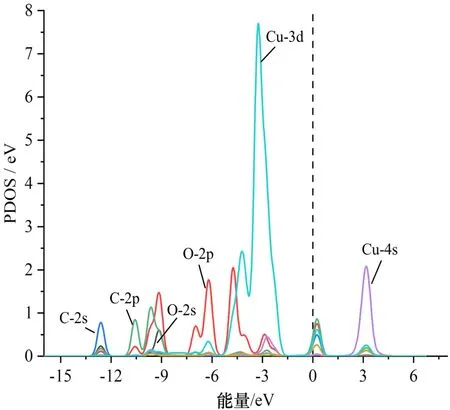
(a)CF2O的C、O原子与CuO的Cu原子PDOS

通过分析可知HF与CF2O分子与CuO-C3N之间均存在强烈的化学吸附作用，相互邻近的原子之间产生了新的化学键，使得CuO-C3N吸附HF、CF2O气体更加稳定，另外CF2O在CuO-C3N表面的吸附效果要弱于HF.

3.3 电荷转移量与差分电荷密度

电荷转移量是判断气体与吸附材料之间相互作用强弱的另一重要参量，绝对值越大的QT往往对应着越强的吸附作用[17]. 通过电荷转移量还可以判断吸附过程中气体分子的电子性质. 电荷转移量QT的公式定义为[18]：

QT=Qabsorbed gas-Qisolated gas

(4)

其中Qisolated gas和Qabsorbed gas分别表示气体分子吸附前和吸附稳定后携带的电荷量. 若电荷转移量为负数，则表明在吸附过程中电荷从基底材料转移到气体分子，若为正数则转移路径相反. 通过静态计算得出CF4、C2F6、CF2O、HF在本征C3N和CuO-C3N上的电荷转移量如表2所示.

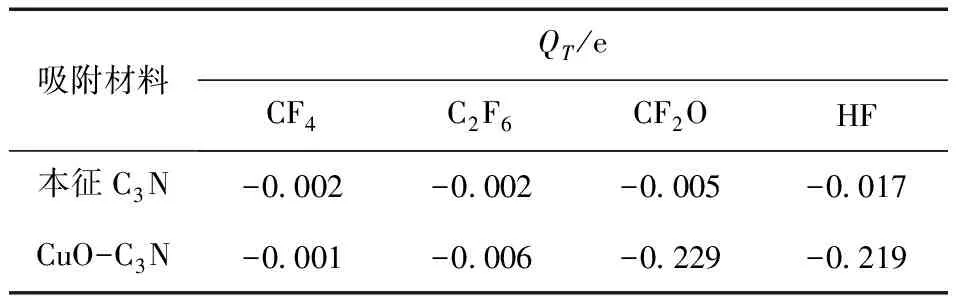
表2 电荷转移量

这四种气体吸附本征C3N和CuO-C3N后引起的电荷转移量均为负值，气体分子将从吸附材料表面获得电子，表现为电子受体的性质. 从数据分析，CF4、C2F6、CF2O、HF在本征C3N上的电荷转移量十分微小，在 0.02e范围内，说明本征C3N对C5F10O分解气体的敏感性极差. 对比本征C3N，CF4、C2F6在CuO-C3N表面的电荷转移几乎没有改变，而CF2O和HF的QT明显增大，超过了0.2e，这说明CF2O、HF与CuO-C3N表面的相互作用较为强烈，CuO-C3N对CF2O和HF两种气体极为敏感. 但由于HF分子本身发生断键，电荷转移机理较为复杂，无法仅凭电荷转移量进行判断，因此将从差分电荷密度作进一步分析.

为了深入了解气体在吸附过程中的电荷转移情况，通过定义计算了四种吸附体系的差分电荷密度，公式如下：

Δρ=ρmol/CuO-C3N-ρmol-ρCuO-C3N

(5)

式中ρmol/CuO-C3N为吸附体系的电荷密度；ρmol与ρCuO-C3N分别为吸附后气体分子与CuO-C3N表面的电荷密度[19]. 利用计算式最终得到气体分子吸附于表面的差分电荷密度图，由于CF4与C2F6在吸附过程中转移给吸附基底的电荷非常少，因此图8a、b为5.0×10-4eÅ-3等值面下的差分电荷密度图，图8c、d则为0.02 eÅ-3等值面下的差分电荷密度图. 其中，蓝色代表电荷损耗区，红色代表电荷聚集区.

图8 差分电荷密度Fig. 8 Charge density differences

在CF4吸附体系中，电子聚集区和损耗区都分布在CF4和CuO分子周边，且因为距离较远，CF4与CuO周围的电子云几乎没有产生接触，说明电荷转移主要发生在分子内部而不是气体分子与CuO分子之间. 另外，Cu原子周围有一极小的电荷损耗区，说明CuO-C3N中的Cu原子在吸附CF4的过程中失去微量电子. C2F6吸附体系的情况与CF4体系十分相似，但Cu原子周围的损耗区稍微扩大了一些. 上述现象都说明了CuO-C3N与CF4、C2F6之间所发生的反应都较弱，电荷转移十分微量，但基底对C2F6的吸附能力要稍强于CF4，这与在前文分析出的结果相对应.

反观图8c和图8d，有大范围的电荷聚集和损耗区出现在气体分子和基底之间，且两者周围的电子云紧密重叠在一起，这表明两种气体分子与CuO-C3N发生了相当强烈的吸附反应. 其中，对于CF2O吸附体系，电荷聚集区主要分布在CF2O周围，而损耗区主要集中在Cu原子上，因此在吸附过程中Cu原子会将电荷转移给CF2O分子，吸附基底表现出电子给体的性质. HF与CuO-C3N之间的电荷转移情况要略微复杂一些，O原子周围有少量的电荷聚集区，H原子上部则存在电荷损耗区，这说明H原子会将少量的电荷转移给O原子；F原子和Cu原子周围分别存在着大面积的电荷聚集区与电荷损耗区，表明F原子从Cu原子处获得了大量的电荷，使得HF分子整体表现为得电子的性质. 总的来说，CuO-C3N与CF2O、HF之间的电荷转移作用十分强烈，CuO-C3N对这两种气体表现出强烈的吸附作用.

总的来说，四种气体分子在吸附过程中从CuO-C3N得到电荷，呈现出电子受体的性质，均为p型吸附. 但CuO-C3N吸附CF2O和HF气体后引起的电荷转移程度较高，而CF4和C2F6发生吸附后的电荷转移及其微弱. 因此可以确定CuO-C3N与CF2O、HF这两种气体之间的相互作用较为强烈.

3.4 恢复时间

恢复时间(τ)表示的是从材料表面去除吸附的气体分子所需要花费的时间[20]. 恢复时间越长表明气体在基底材料上吸附得越牢固，气体分子越难从材料表面脱除. 根据传统过渡态理论，恢复时间τ可表示为：

τ=F-1e(-EB/KBT)

(3)

式中，KB与T分别表示玻尔兹曼常数和开尔文温度；F为尝试频率，此处设为1012s-1；EB为解吸附时的能垒，与吸附能大小相等[20]. 从计算公式可以看出，吸附能与恢复时间有直接关系. 表3为四种气体在不同温度下从CuO-C3N材料表面脱附所需的时间.

表3 不同温度下的恢复时间

在室温下，CF4和C2F6的解吸附速度就已极快，仅需不到1ms的时间，充分说明这两种气体在CuO-C3N表面的吸附极不稳定，CuO-C3N无法实现对这两种气体的有效去除. 常温环境下CF2O从CuO-C3N表面脱附需要十几分钟的时间，且恢复时间会随温度的升高而缩短. 即使CuO-C3N初期可以与CF2O之间发生较为强烈的吸附作用，随着时间的延长，该气体还是会从材料表面解吸附. 反观HF气体，在25℃的温度下其恢复时间竟长达数十年，说明在正常温度下HF基本无法从CuO-C3N材料上脱附. 即使在超过100℃的高温环境下，HF的脱附时间也需要将近三年. 从分析结果看，CuO-C3N材料可以作为一种高性能的气体吸附剂，选择性去除C5F10O绝缘设备内部及环境中的有毒HF气体.

综上所述，相较于本征C3N，C5F10O分解组分与CuO-C3N材料之间的相互作用均具有一定程度的增强. CuO-C3N对HF的吸附效果最好，CF2O次之，几乎无法吸附CF4与C2F6. HF气体在吸附表面会更易分解且吸附量最大，这会降低CuO-C3N材料对CF2O气体的吸附强度，极大提高CuO-C3N对HF气体选择性吸附能力.

4 结 论

本文基于第一性原理构建了四种C5F10O放电分解组分(CF4、C2F6、CF2O、HF)在本征C3N与CuO掺杂C3N表面的吸附模型，主要计算了四种气体分子在CuO-C3N表面吸附时对应的一系列表征吸附性能的参量，通过对比分析得出以下结论：

1)经过CuO掺杂后的C3N对于CF4、C2F6、CF2O与HF气体的吸附效果有非常明显的增强.

2)通过比较吸附能、吸附结构与态密度，确定CuO-C3N吸附四种气体的强弱为HF>CF2O>C2F6>CF4，其中HF和CF2O与CuO-C3N之间已经产生新的化学键，形成较为强烈的化学吸附，而其余两种碳氟类气体均为物理吸附. 通过比较电荷转移量与差分电荷密度，确定C5F10O放电分解组分吸附于CuO-C3N后的电荷转移程度依次为HF>CF2O>C2F6>CF4，且四种气体分子在吸附过程中得到电荷，呈现出电子受体的性质.

3)通过对恢复时间的分析发现在298-598 K的温度区间内，随着环境温度的增加，只有HF能够稳定吸附于材料表面.最终确定CuO-C3N可以在C5F10O分解组分中实现对HF有毒气体的选择性去除.其可以作为一种高性能的吸附剂应用于C5F10O环保绝缘气体的废气处理领域.