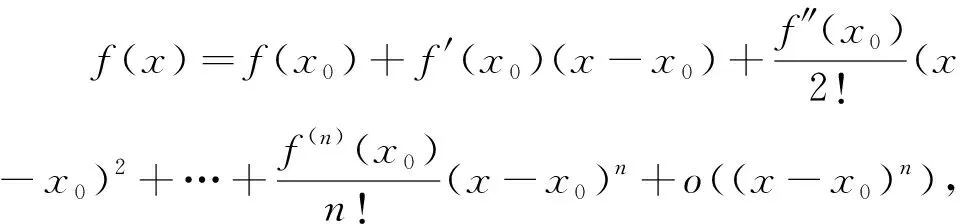对2023年全国乙卷文数第20题的深度探究*

郭 蒙

陕西省榆林市吴堡中学 (718200)

1 试题呈现

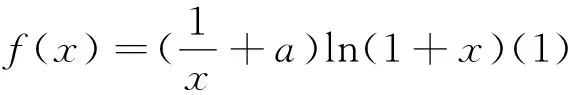
这道高考题,第一问常规题目,难度上进行了合理控制,体现了学科知识本质的基础性,落实了高考内容改革,考查学生对基础知识和基本方法的深刻理解及融会贯通的应用,落实“四翼”考察要求,聚焦学科核心素养,计算量大,是一道非常精彩的压轴题,彰显了试题的综合性,符合选拔高层次人才的要求.

2 解法探究

2.1 第(1)问求解

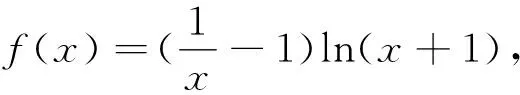
评注：第(1)问属于常规题型,利用导数容易求出曲线y=f(x)在点(1,f(1))处的切线方程,突出强调对基础知识和基本技能的深入理解.

2.2第(2)问求解解法一(必要性探路-端点效应)

命题1 若h(x,m)≥0(m为参数)在[a,b](a,b为常数)上恒成立,且h(a)=0(或h(b)=0),则h′(a)≥0(或h′(b)≤0).

命题2 若h(x,m)≥0(m为参数)在[a,b](a,b为常数)上恒成立,且h(a)=0,h′(a)=0或(h(b)=0,h′(b)=0),则h″(a)≥0(或h″(b)≤0).

证明1：因为h(x)≥0在[a,b]上恒成立,且h(a)=0,因此存在t∈(a,b],使得h(x)在[a,t]上单调递增,所以h′(x)≥0在[a,t]上恒成立,因此h′(a)≥0.(h′(b)≤0证明方法类似)

证明2：因为h(x)≥0在[a,b]上恒成立,且h(a)=0,因此存在t∈(a,b],使得h(x)在[a,t]上单调递增,所以h′(x)≥0在[a,t]上恒成立,又因为h′(a)=0,因此存在δ∈(a,t],使得h′(x)在[a,δ]上单调递增,所以h″(x)≥0在[a,t]上恒成立,因此h″(a)≥0.(h″(b)≤0证明方法类似)

推论1 若h(x,m)≥0(m为参数)在[a,b](a,b为常数)上恒成立,且h(a)=0,h′(a)=0,…,h(n-1)(a)=0,则h(n)(a)≥0,n≥1,n∈N.

推论2 若h(x,m)≥0(m为参数)在[a,b](a,b为常数)上恒成立,且h(b)=0,h′(b)=0…,h(n-1)(b)=0,则h(n)(b)≤0,n≥1,n∈N.

评注：必要性探路方法求出的参数范围并不一定就是所求的实际范围,必须检验其充分性,利用必要性探路可以缩小参数的讨论范围,减少分类讨论的类别,降低思维的成本.

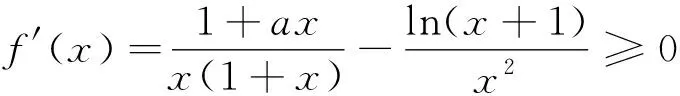
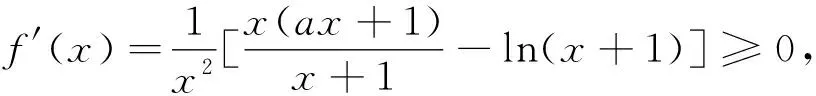
评注：本题可转化为端点效应题型,并且充分性成立,充要性得证端点效应为我们用分类讨论解题提供了参数的分界点,利用端点效应可缩小参数的范围,使得分类讨论的问题得到简化.

当a≤0时,g′(x)<0,g(x)在(0,+∞)上单调递减,g(x)

评注：利用必要性探路可得到参数的分界点,以此分界点展开分类讨论,进而完美的解答了此题.

评注：本题利用分离参数法求出了参数范围,导函数比较复杂,计算量较大,还要利用大学知识洛必达法则求极限.

评注：泰勒公式可以帮助我们明确出题人的命题思路,看透题目的本质,以泰勒公式为背景命题,立意新颖,创新性极高,为学生高等数学的学习做铺垫,具有选拔人才的作用,再利用高观点可以溯其源,究其本,在考试时,可以利用泰勒公式迅速得到参数的答案,做到心中有数,利用分类讨论等方法完美解答问题.