例谈三角形面积公式的应用

彭 朴

上海市嘉定区安亭高级中学 (201805)

一、试题呈现

题目如图1,线段AB的长为8,点C在线段AB上,AC=2.点P为线段CB上任意一点,点A绕着点C顺时针旋转,点B绕着点P逆时针旋转.若它们恰重合于点D,则△CDP的面积的最大值为________.(2022学年第二学期上海市高三年级质量调研第11题)

图1

如何来解这道题,不妨先分析一下题目的条件,由条件可知DC=AC=2,CP+DP=6,要求△CDP的面积的最大值,首先要知道如下的三角形面积公式:

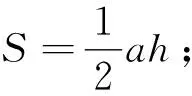
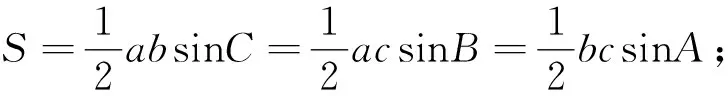
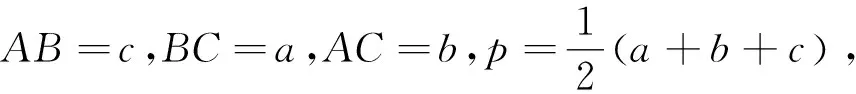
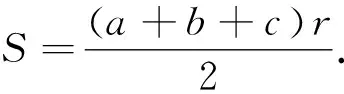
二、解法探究

评注：海伦公式最大的优势是只要知道三角形三条边,就可以把三角形的面积公式求出来,此题虽然只知道一条边长,但另两条边的和知道,只要假设其中一条边长为x,另一条边长就可以用6-x表示,则SΔCDP可以表示为x的函数,转化为求函数的最值.

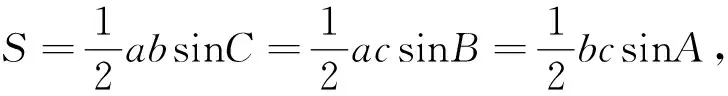
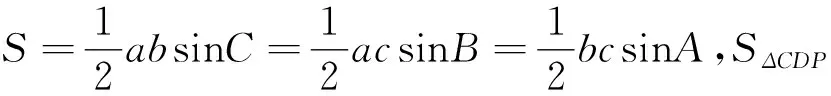
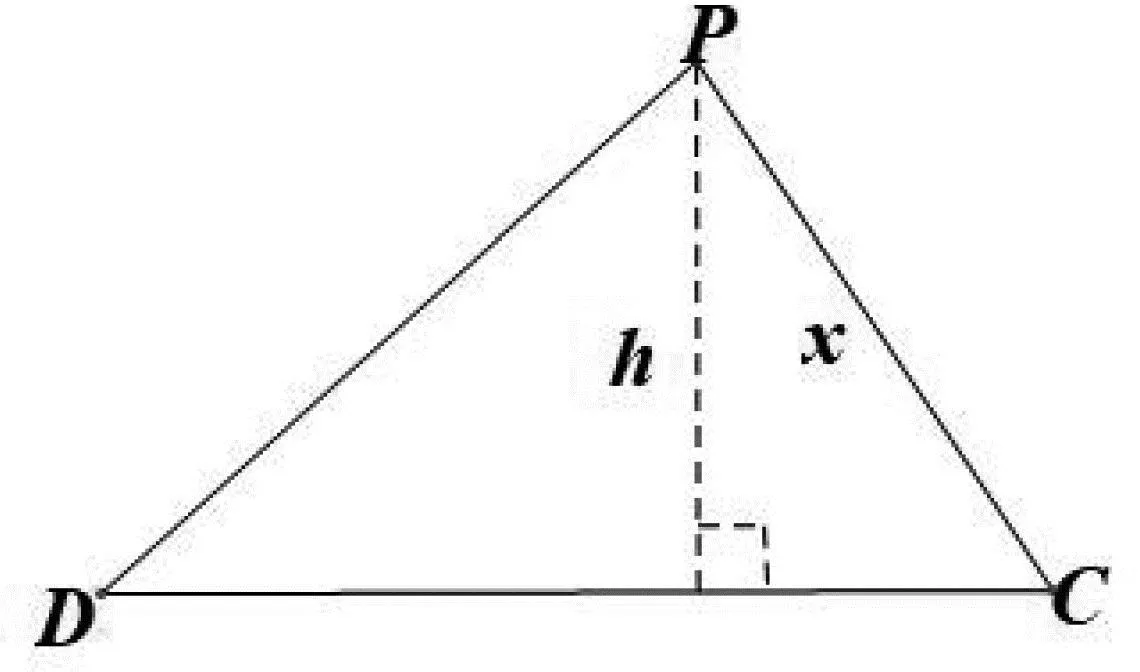
图2

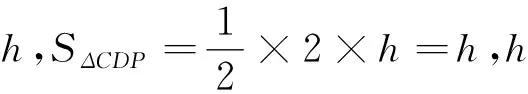
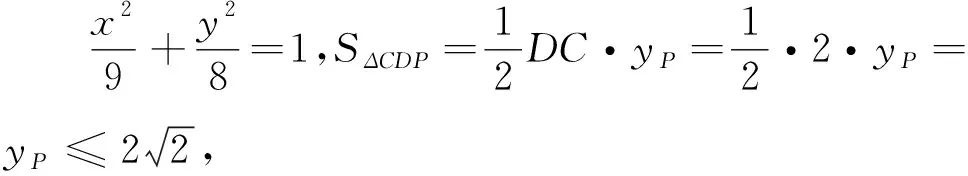
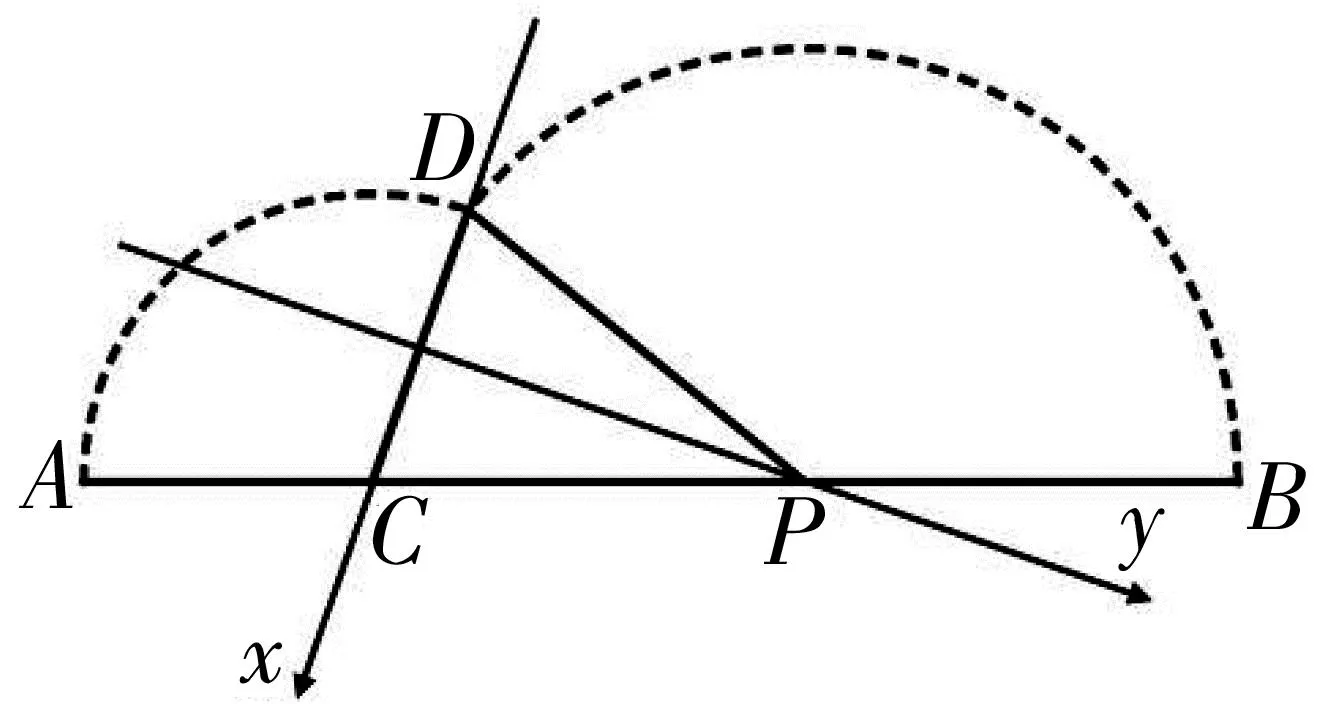
图3

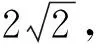
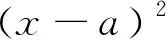
图4

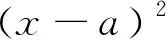
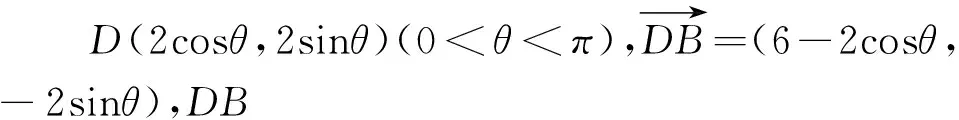
评注：解法6同样是运用解析几何的方法,先建系,然后引进参数θ,将点D坐标用θ表示,写出DB的中垂线方程,求出点P的坐标,计算出|CP|,将SΔCDP表示为θ的函数,最后求出其最值.

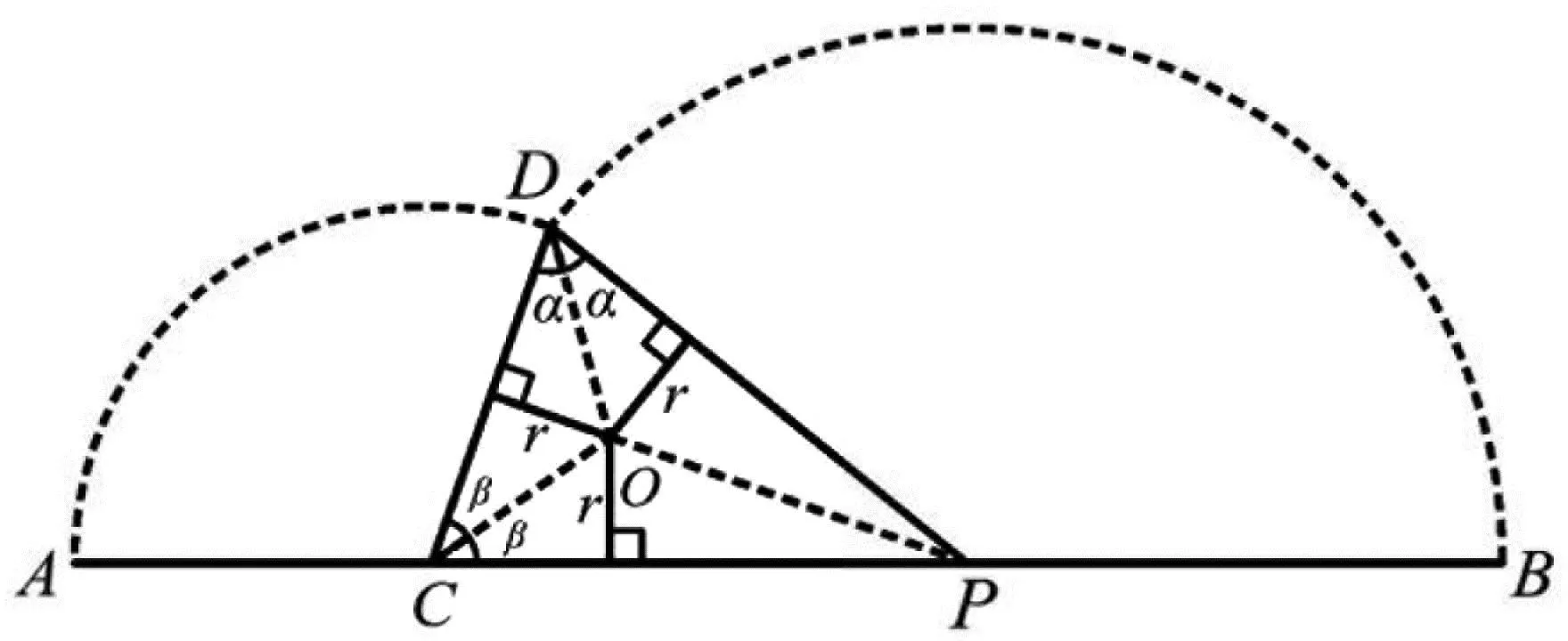
图5

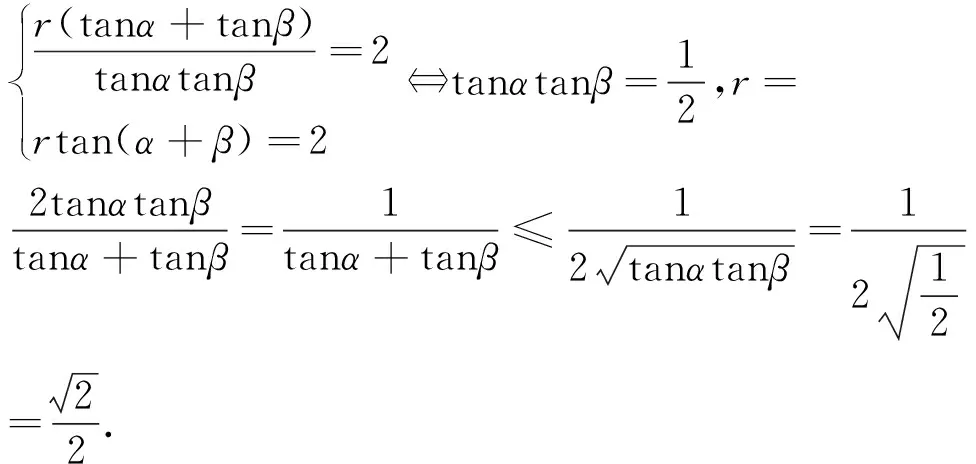
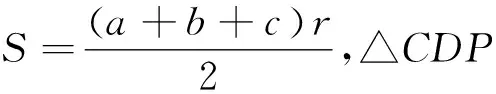
三、结语

以上解法1,2,3和7是采用代数的方法,解法4,5和6是采用解析几何的方法,它们的共同特点是寻找变量,建立SΔCDP关于变量的函数关系式,转化为求函数的最大值.从上面的推导过程中,容易得到以下结论:当三角形的周长和其中一条边为定值,另两条边相等时,此三角的面积最大.

这道试题综合考查了三角形面积公式的应用、函数关系式的建立、求函数的最值等基本知识、技能和方法,建立函数关系式是本题的关键,既可从代数的角度直接转化,也可从几何的角度转化,是考查数学思想方法的良好素材,也是考查直观想象、逻辑推理、数学运算核心素养的好试题.