基于“四个理解”的教学实践探究——以“圆锥曲线的共同特征”为例*

涂文娟 赵启正 易桂生

江西师范大学数学与统计学院 (330022)

1 引言

2017年4月,在“以核心素养为纲的数学教学改革”的研讨会上,章建跃博士完善了“四个理解”,即理解数学、理解学生、理解技术、理解教学.基于“四个理解”设计高中数学教材中的“阅读材料”是用好教材、发展学生核心素养的有效途径.近日,笔者有幸在《基于数学核心素养理念的“同课异构”》教研活动中设计并展示了高中数学“圆锥曲线的共同特征”示范课.现把这节课的教学过程及思考整理成文,以飨读者.

2 “四个理解”下的教学设计要点

基于“四个理解”设计的教学内容及要点如下:

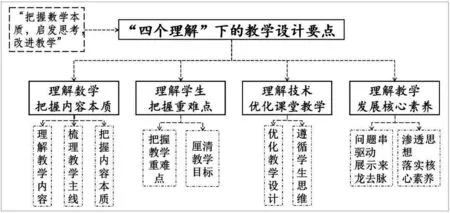
3 “四个理解”下的教学实践

3.1 理解数学,把握内容本质

(1)理解教学内容

当学生对教学内容的理解停留在表层时,对课堂上所学的概念往往都表述不清楚.所以,在正式授课之前,教师要做好“教学内容的教学理解”[1],把握教学内容的数学本质,设计教学,让学生理解学习内容,启发学生思维发展.

如何把握教学内容的数学本质呢?张奠宙教授指出,“一个知识的数学本质包括数学知识的内在联系;数学规律的形成过程;数学思想方法的提炼;数学理性精神的体验等诸多方面[2]”.除了知识技能,还应注重渗透数学思想、揭示知识结构等等.

“圆锥曲线的共同特征”选自北师大(2019年)版高中数学必修第一册第二章第四节阅读材料.主要是介绍共同特征以及统一定义,“平面上到定点距离与到定直线(定点不在定直线上)距离比值为常数k(>0)的点的轨迹是圆锥曲线”.

解析几何是高中数学的重难点内容,其本质思想是“用代数方法研究几何问题”.“圆锥曲线”作为解析几何的重点内容,是渗透其本质思想的重要载体.所以,本节课的重点在于如何将“共同特征”及“统一定义”等内容揭示出来,同时渗透知识点背后蕴含的类比、数形结合、坐标法等数学思想.

(2)梳理教学主线

教材上本章是按照椭圆、双曲线、抛物线的顺序展开,教学遵循“曲线的几何特征——曲线的标准方程——通过方程研究曲线的性质一应用”,并把椭圆作为重点,强调它的典型示范作用,注重数学思想和基本方法的引领性[3].”

教学主线是教学设计的灵魂,贯穿始终.本节课的教学主线依照“直观感知迁移类比归纳概括代数验证”,知识技能(定理、验证)和数学思想(类比、数形结合)形成两条线,从导入(发现问题、提出问题),到猜想(分析问题),再到探究、验证(解决问题),脉络清晰.与前面学习相似,同样把椭圆作为重点.其主线关系如下:

(3)把握内容本质

本节课的研究目标是三类圆锥曲线的共同性质,其内容本质是抽象概括圆锥曲线统一的定义形式,渗透解析几何的本质思想,感悟数学的和谐统一美.在整个过程中,先借助GGB动画展示改变距离比值k(k>0)形成的动点轨迹,依靠“形”发现共同特征;再数形结合从代数角度探究、验证共同特征.

3.2 理解学生,把握重难点

(1)把握教学重难点

理解学生,首先要清楚学生已有的知识经验和思维方式,把握整节课的教学重点、教学难点,这是教学最有力的脚手架.

本节课之前,学生已经会用代数眼光去看待几何问题.比如说,在研究“直线与圆有多少个交点”问题时,会想到联立直线与圆的方程,通过判断方程解的个数解决问题.通过本章前面的学习,感悟到“通过几何建立直观,通过代数建立表达是其基本理念[3].”

但前面的学习属于三类圆锥曲线的个性研究,学生不易猜想出共同特征,更不易联想到用方程验证共同特征.所以本节课的教学重点是掌握圆锥曲线的共同特征和统一定义,从“图形”和“代数”两个角度体会共同特征,感悟类比、数形结合的数学思想,再次领会解析几何的本质—用代数方法研究几何问题.教学难点为应用方程从代数角度验证椭圆、双曲线的共同特征,并抽象概括.

(2)厘清教学目标

理解学生,便于我们厘清教学目标.示范课的教学目标以知识技能为载体将核心素养渗透其中,使得教学目标可观.其目标为:

①了解本节课学习对象、主要学习内容、研究方法等;

②经历生成圆锥曲线的过程,从几何直观上初步感知圆锥曲线的共同特征;借助几何直观感知当比值k改变时,圆锥曲线形状也发生相应改变,构建直观模型,发展直观想象核心素养;

③掌握焦半径、准线等概念,经历化简椭圆焦半径的过程,体会应用方程验证圆锥曲线的共同特征,培养逻辑推理和数学运算等核心素养;

④用统一的代数式抽象概括圆锥曲线的共同特征,体会三种语言之间的转换,感悟数学的和谐美、统一美,发展数学抽象等核心素养.

3.3 理解技术,优化课堂教学

(1)优化教学设计

高中数学学习较为抽象,信息技术可作为应用于数学教学的一种认知工具和数学学习的一部分,应用数字、图形和符号,为抽象的数学理论构建一个直观、动态的模型.如何展示当距离比值k(k>0)变化时点的轨迹?数字与图形变化的同步性,需要借助作图工具.笔者借助GGB展示动点的轨迹生成过程,首先拉近了与学生的距离,营造轻松的学习环境;同时将“不可言传”的内容“可视化”.体现数学味的同时,解决了“粉笔+黑板”不能或者不便于解决的教育教学问题,优化了教学设计(如图1).

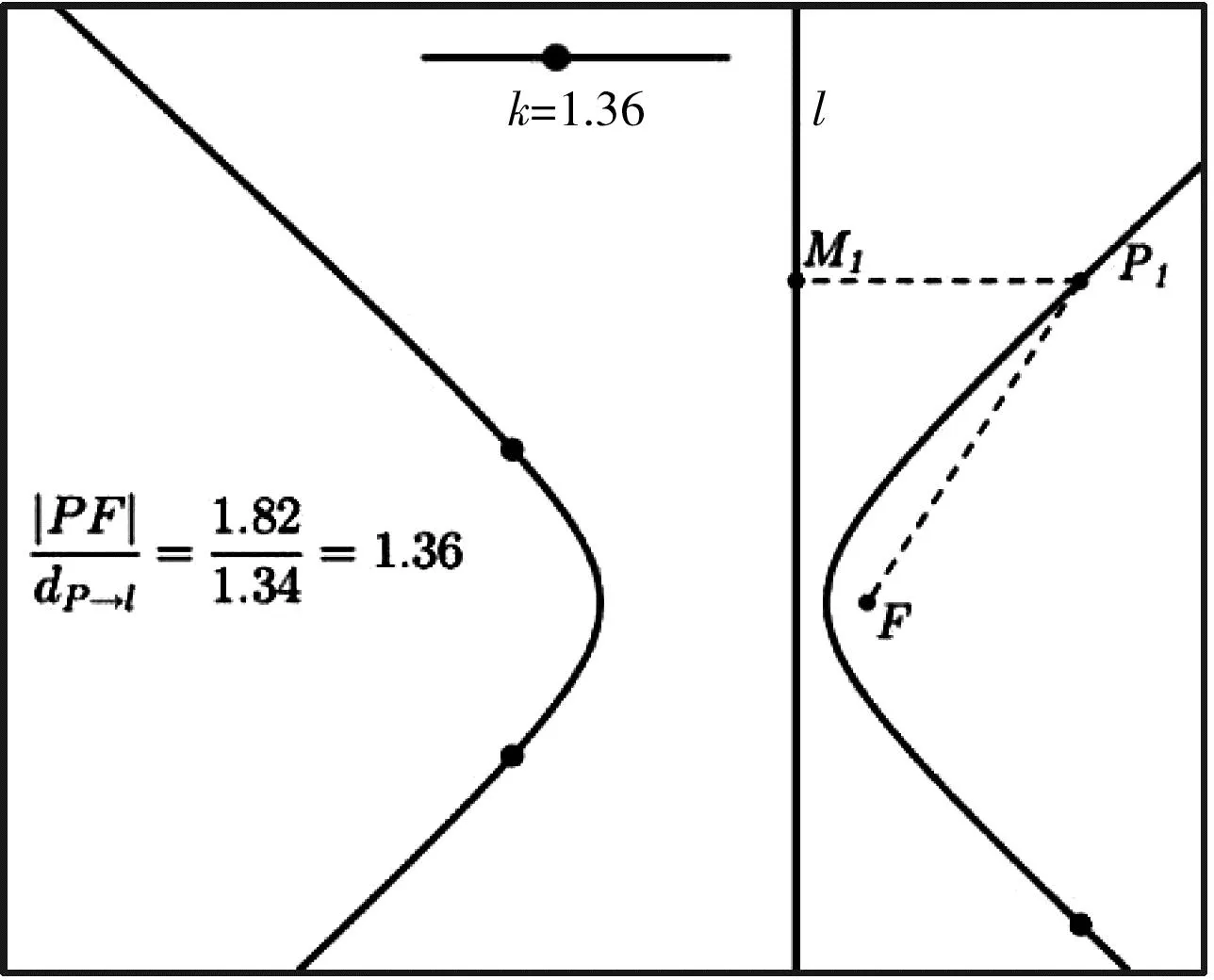
图1 GGB动画展示动点轨迹

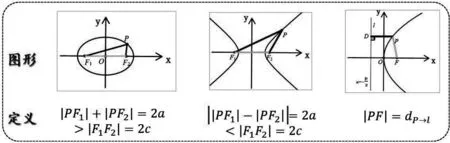
图2 三类圆锥曲线的定义

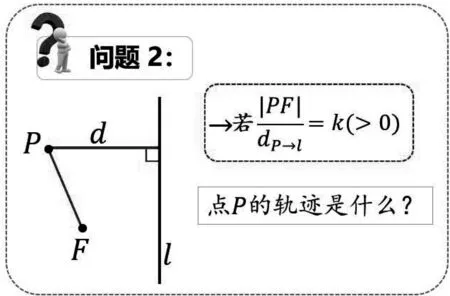
图3

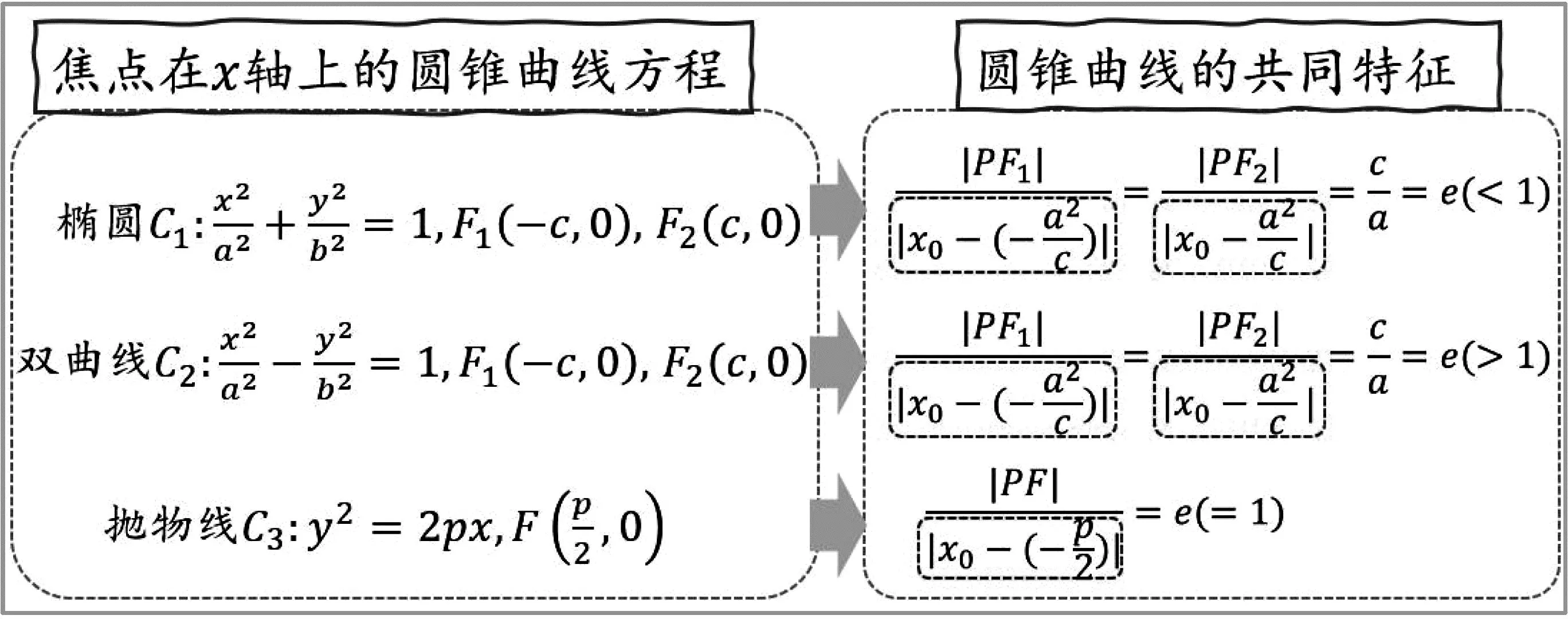
图4

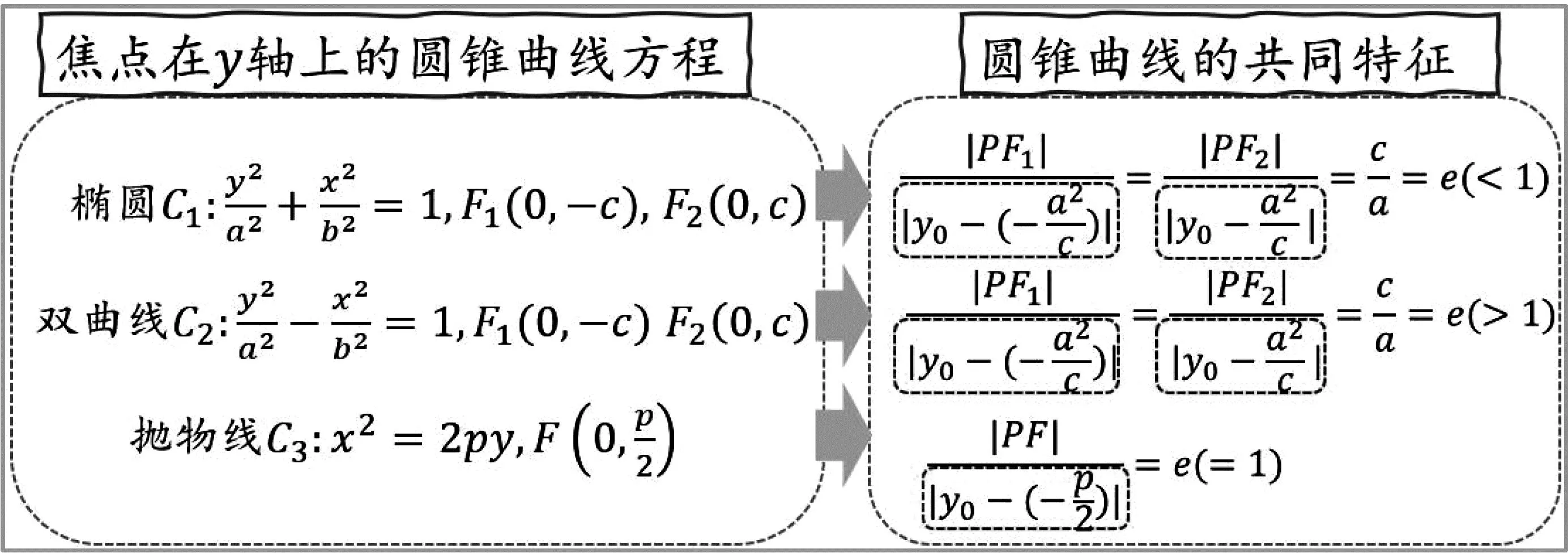
图5

(2)遵循学生思维

示范课上,借助作图工具从几何直观上展示随着距离比值k的慢慢增大,动点P的轨迹依次是椭圆、抛物线、双曲线,再抽象概括得到圆锥曲线的共同特征,最后代数验证.这样的顺序符合学生的认知过程,先几何后代数、先具体后抽象,遵循了由浅入深的思维发展.

3.4 理解教学,发展核心素养

(1)问题串驱动,展现知识的来龙去脉

“问题是数学的心脏”,设计问题串驱动教学,使学生置身于数学情境中,提高发现问题、提出问题的能力.本节课由5个大问题贯穿,在层层递进的问题中培养学生分析问题和解决问题的能力.

问题1 三类圆锥曲线的定义是如何描述的?

设计意图:回顾旧知,可以帮学生快速定位,明确当下任务.对比三者定义发现,椭圆、双曲线描述的是平面内到两个定点距离和、差的点的轨迹,而抛物线刻画的是到焦点与准线距离比值相等的点的轨迹,同作为圆锥曲线,肯定会存在共同的性质,共同性质是什么呢?这是很自然的提问,也顺势引出接下来的内容.

问题2若到定点与定直线距离比值为常数k(k>0),动点P的轨迹会是什么?

设计意图:从不同的抛物线的定义出发,将距离相等改成距离比值的形式,构造动态动态参数k(k>0),探究动点P的轨迹.

问题3通过GGB动画展示,可以得到哪些结论?你能用数学式子表示吗?

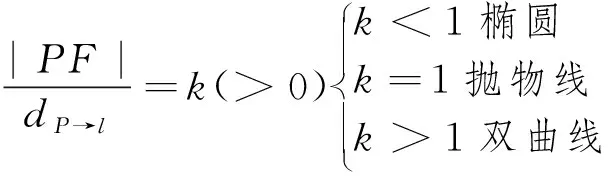
追问:由此你能概括它们的共同特征吗?

设计意图:GGB动画演示的过程中渗透着数形结合思想(满足两个条件的点的集合可以看作是圆和直线的交点);利用子问题逐步引导学生概括圆锥曲线的共同特征.

问题4三类圆锥曲线的几何性质有哪些,我们是如何探究并验证的?

示范课之后,专家点评道,这个问题略显生硬,现场的学生并不能明白需要回答的问题,改进之后的问题为:前面学习了椭圆的对称性.在椭圆上任意取点P,则P点关于原点的对称点P1、关于x轴的对称点P2是否在椭圆上?

预设(生1):椭圆是中心对称图形,根据图像和定义可以确定.

预设(生2):xP1=-xp,yP1=-yp;xP2=xP,yP2=-yP,点P1,P2的坐标都满足方程.

补充:根据图形初步猜测几何性质,利用方程可以验证结论.

追问:类似地,椭圆的共同特征(共有性质)应该如何验证呢?

设计意图:前面分别学习三类圆锥曲线的几何性质,而共同特征是它们共有的几何性质.运用类比,以椭圆(焦点在x轴上)为例,只要证明其上任意一点P(x0,y0)到焦点距离与到准线距离比值等于离心率e,即证明椭圆的共同特征.渗透类比、数形结合的思想,启发学生仿照之前的学习用标准方程(代数)去验证共同特征.

问题5你能类比椭圆验证双曲线的共同特征吗?

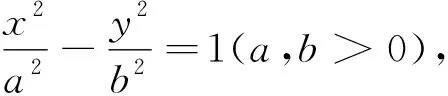
接下来,将焦点在x轴上的椭圆、双曲线的共同特征,用数学代数式抽象概括出来.

追问:焦点在y轴上的椭圆、双曲线如何其验证共同特征?

学生:同样地设出标准方程,设点P(x0,y0),再化简焦半径|PF2|、|PF1|.

(2)渗透思想,落实核心素养

接下来就是给出“统一定义”,回顾整节课的思路:“发现问题(同是圆锥曲线,应该存在共同性质)——提出问题(圆锥曲线的共同特征是什么)——分析问题(从抛物线的定义出发,构建距离比值参数k,探究动点P的轨迹)——解决问题(GGB演示轨迹形成,类比椭圆,从代数角度验证共同特征,抽象概括共同特征)”.整节课遵循“先用平面几何观察,再用坐标法推理、论证”指导思想[3].

整节示范课以学生为中心,以问题为抓手,循序渐进的问题是学生思维的落着点,也是知识点发生发展的枢纽.从几何直观—动手演示—代数验证,无一不体现数学的严谨性和科学性,类比、数形结合等思想渗透其中.整个过程培养学生的逻辑推理、数学运算及直观想象素养,渗透解析几何的本质—用代数方法研究几何问题.

4 结语

《标准》指出,“在教学实践中,要不断探索和创新教学方式,不仅重视如何教,更要重视如何学,引导学生会学数学.”基于“四个理解”思考如何揭示本质、优化教学是落实“教什么”及“如何教”的有效途径.此外,“数学是思维的体操”,而问题是思维的起点,如何设计问题串驱动教学;如何做好过程性评价是值得深入思考的.