“生长数学”在发展初中数学核心素养中的认识及实践

何丽娟

安徽省合肥市巢湖市第三中学(238000)

生命的价值在于成长,教育的价值在于促进学生的内在生长.数学教学的价值在于提供与内在生长、生命成长相匹配的正能量,这种正能量就是生长数学下的教学行为.生长数学的价值取向是基于旧经验生长新知识.在这个过程中,亟需关注知识的生长、生命的生长、智慧的生长、境界的生长.随着课程改革的深入,“教学价值是教学设计的灵魂”这一带有哲学思辨性的命题更加引发人们的关注和重视.新课程实践中,有观点认为“教什么永远比怎么教重要”.而“教什么”的关键在于把握教学资源的教育价值,既要挖掘教学资源的“表象价值”和“原生价值”,更要将隐藏在教学资源中的“表象价值”和“原生价值”之后的价值开发出来.

一、“生长数学”的根本所在:教育价值

课程标准指出,义务教育数学课程的总体目标是“四基”、“四能”,“使学生获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想和基本活动经验”,“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系,运用数学的思维方式进行思考,增强发现和提出问题的能力、分析和解决问题的能力”.为了实现上述目标,可以在教学过程中努力做到“三到”:

一是从“数学知识”到“学科智慧”.数学是一门聪明的学问,也是一门智慧成长的学问.要体现上述思想,就教材教教材不行,就知识教知识也不行,必须从教材教知识中跳出来,从知识中获得经验,从经验中获得智慧.

二是从“课时目标”到“课程目标”.教学目标是教学活动的起点和归宿.“将数学分解为碎片化的知识,对知识的细枝末节太过重视,在非本质形态上兜转转、做文章,讲究立竿见影,还冠以学数学有用,学数学实惠”,这种数学行为,可以使学生有效地掌握知识与技术.但是,也会让学生只见树木而不见森林.同时,课程目标要依据学生的学习基础、年龄特征和认识水平来确定.

三是从“数学教学”到“数学育人”.数学学习的重要性是人类发展的必然要求.求真、明理、明智、明根、会思,是数学教育的价值所在.运用科学研究方法对待数学,将数学教学作为人类活动的数学教学.要将数学教学视为理性思维的数学,以理性思维来思考数学,以文化素养来对待数学教学,以数学素养来润泽学生心田.

二、“生长数学”的本质需求:核心素质

在“生长数学”中,数学素质的目标追求显得尤为突出.学生通过义务教育阶段的数学学习,可以“得到必要的数学知识、基本技能、基本思想和基本经验,以适应社会的生活,促进社会的蓬勃发展”.利用数学思维方法,可以增强提出问题、分析问题、解决问题的能力,增强其对数学学习的兴趣,使其拥有良好的数学信心.数学核心素养的内涵是数学课程目标的需求,它不仅强调数学应用和现实生活中的特性,更注重学生必须具有适应社会生活的数学素养.数学核心素养的实施途径,可以从数学抽象、数学推理、数学模型三个层面进行探讨:

一是以数学抽象的方式,加强学生的数学意识.学习数学,就是要让学生有数学的视野,并以特定的数学活动来实现有价值的思维.在此,我们要正确认识到数学视野与思维是其它学科所没有的特殊性;同时要学会观测到“数学的结果就是‘看’,而非‘证’的”,“看”和“证”的关系就是要唤醒学生的数学抽象意识,训练数学抽象思考,培养数学抽象能力,从而使学生具有数学视野.

二是以数学推理的活动,培养学生的数学内核.我们知道,与其它学科不同,数学学科具有不同于其它学科的本质特点,而数学推理是影响数学教学中的一个重要内容.如果说,数学抽象是将外部世界中和数学相关的事物纳入到数学中,那么,通过数学推理活动,可以“获取数学的命题和计算方法,推动数学内部的发展”.

三是以数学建模的活动,增强学生的数学素质,并使学生的数学表达能力得到锻炼.学生通过数学模型,在数学和外界世界中搭建一个具有代表性的桥梁,创造出一个具有体现力的数学语言,即让数学将信息传送到外户,让数学进入生活,成为生产力,服务于人类.

三、“生长数学”的生长标志:形成过程

通过不同教学阶段、不同章节内容,学习者能体会同一生长的原理,感悟数学生长中的“形内外”与“正负性”的紧密联系,从而触类旁通、举一反三,其中关键是得到一种学习新知的理念,这是最为珍贵的.

例1 已知∠ABC=α,∠ABD=β(α>β)求∠CBD.

例2 已知三点A、B、C是同一条直线上的三点,AB与BC为线段,如果AB=a,BC=b(a>b),求AC.

图3

图4

上述两例均来自于人教版七年级数学上册第四章《几何图形初步》中介绍角和线段的内容.我们知道,角和线段也正是几何学很重要的两个基本立足点.这两个问题很好地介绍了形内外与代数运算中符号正负性之间的关系.

这个素材中还可以进一步的变形处理,分别取角的平分线和线段的中点,又能得到哪些关系呢?

例3 已知直线AB与直线CD平行,点E,F分别在直线AB与CD上,P为平面内一点(不在直线AB、CD上),连接PE、PF.(1)如图5,探索∠BEP、∠DFP、∠P的数量关系;(2)如图6,探索∠BEP、∠DFP、∠P的数量关系.

例4 在△ABC中,(1)如图7,如果∠ABC、∠ACB的平分线相交,且交点为O,试找出∠BOC与∠A的数量关系;(2)如图8,如果∠ABC、∠ACB的外角平分线相交,且交点为O,试找出∠BOC与∠A的数量关系.

以上两例分别来源于七年级下册第五章《平行线与相交线》,八年级上册第十一章《三角形》.从中我们还是可以体会“形内外”与“正负性”之间的关系.几何学的内容在潜移默化中慢慢的生长开来,并且学习还远远不止就此,实际上,学习者是通过知识获得经验,通过经验感悟成长,通过成长获得智慧的.

例5 如图9,在△CDE中,已知∠DCE=90°,CD=CE,且直线AB经过点C,DA⊥AB,EB⊥AB,垂足分别为A,B.(1)当AB绕点C旋转到图9位置时,判断线段AB与AD、BE的数量关系,并说明理由;(2)当AB绕点C旋转到图10位置时,判断线段AB与AD、BE的数量关系,并说明理由.

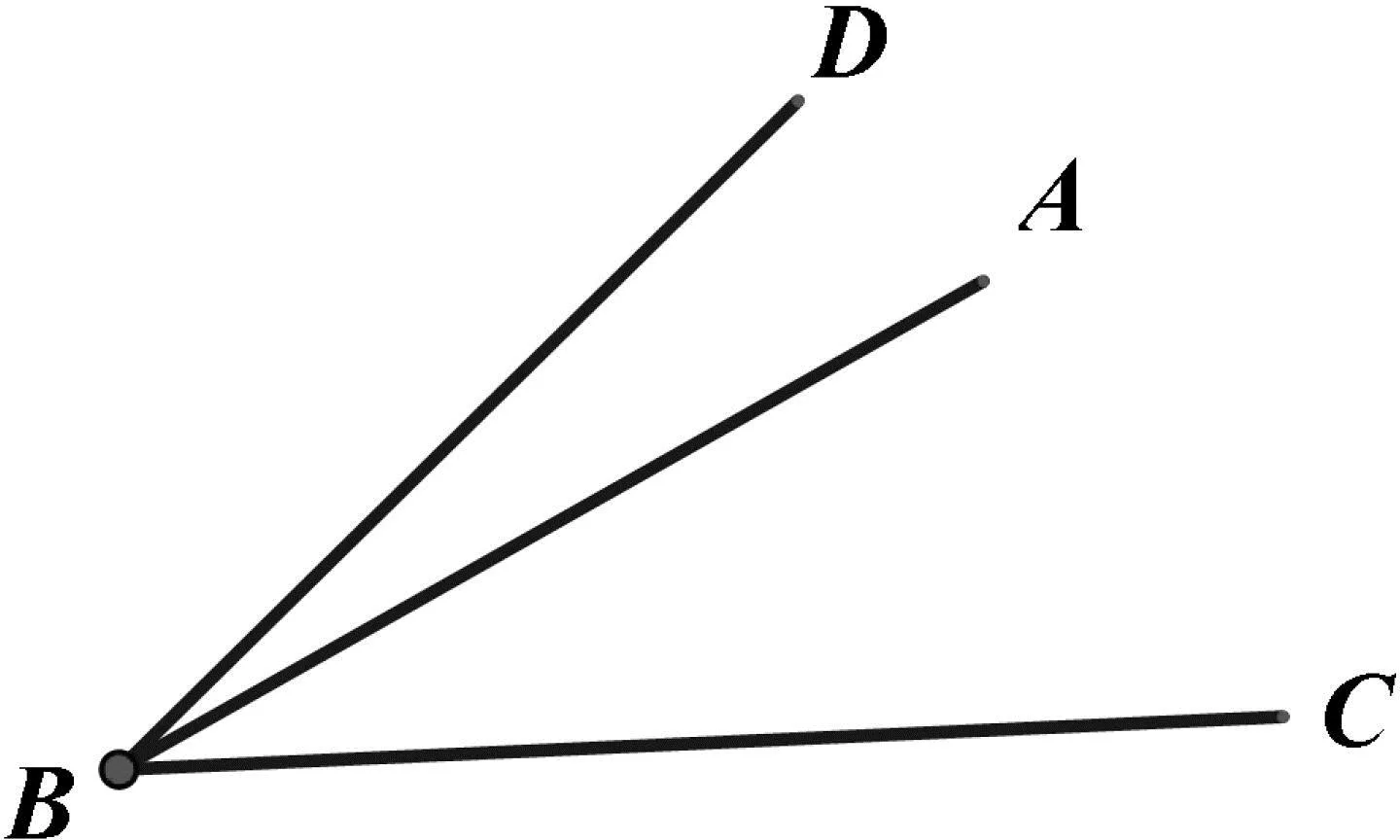
图1

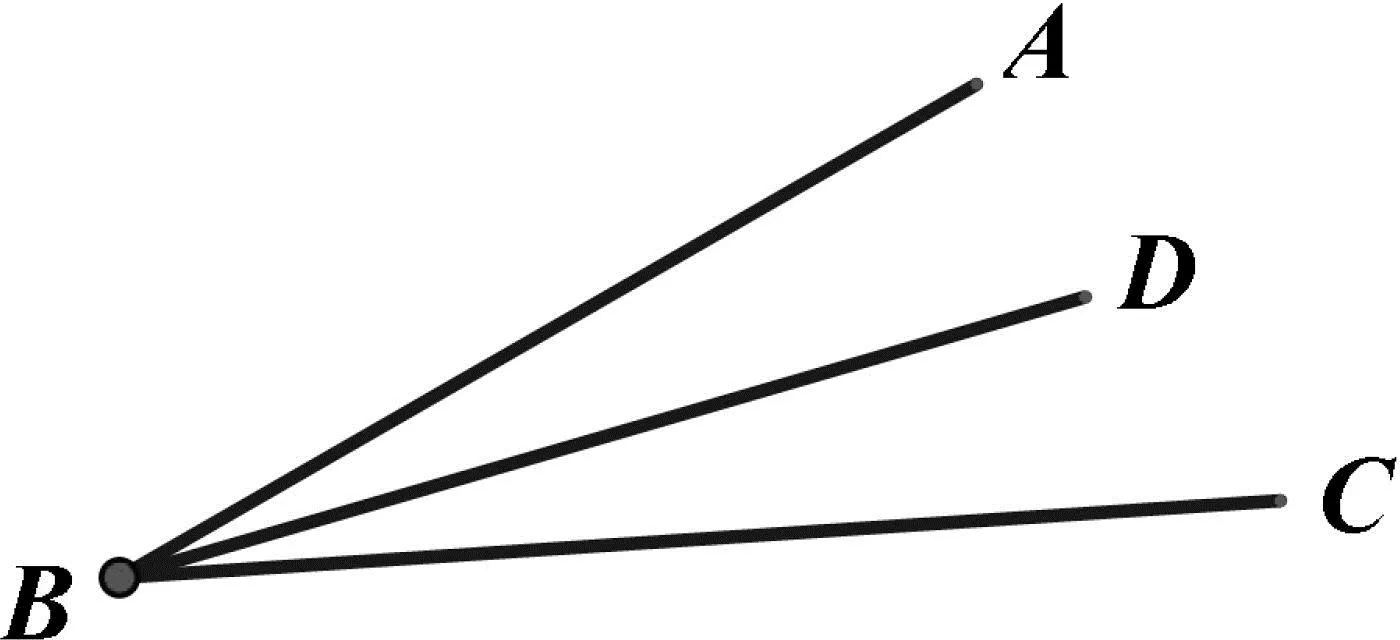
图2

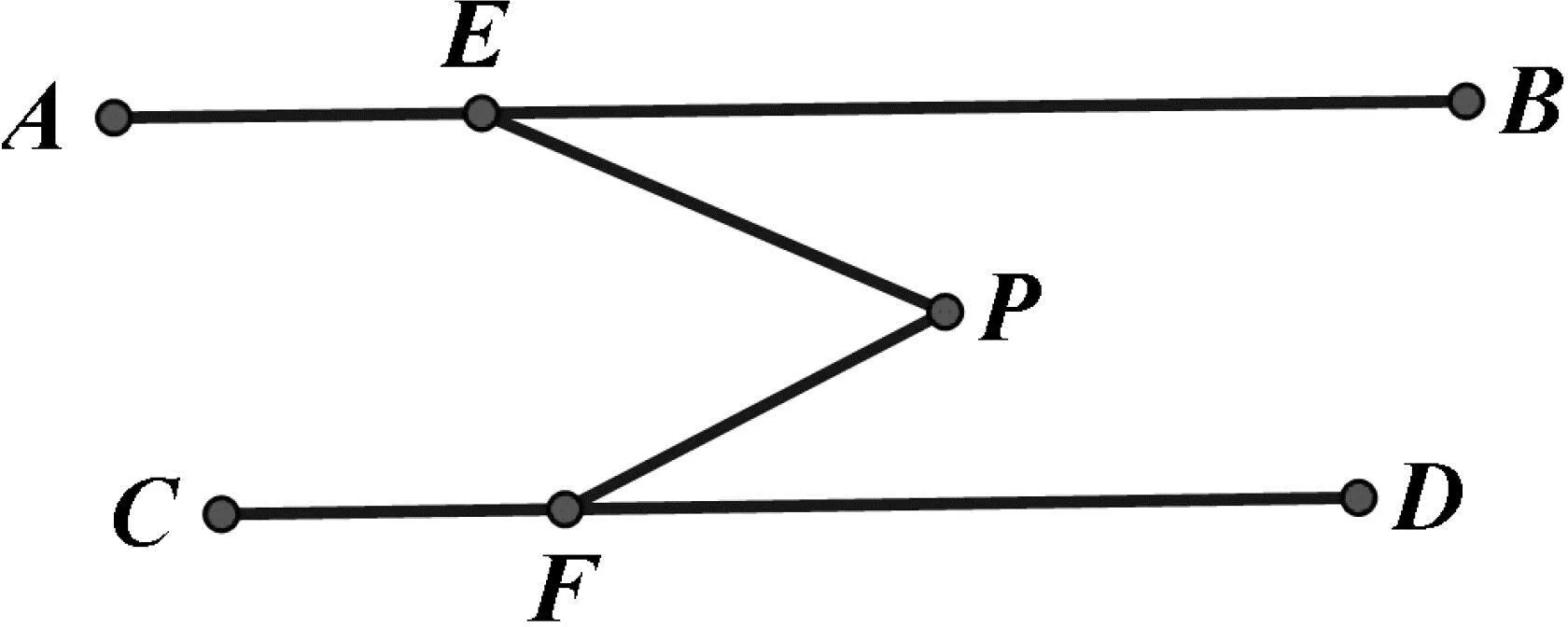
图5

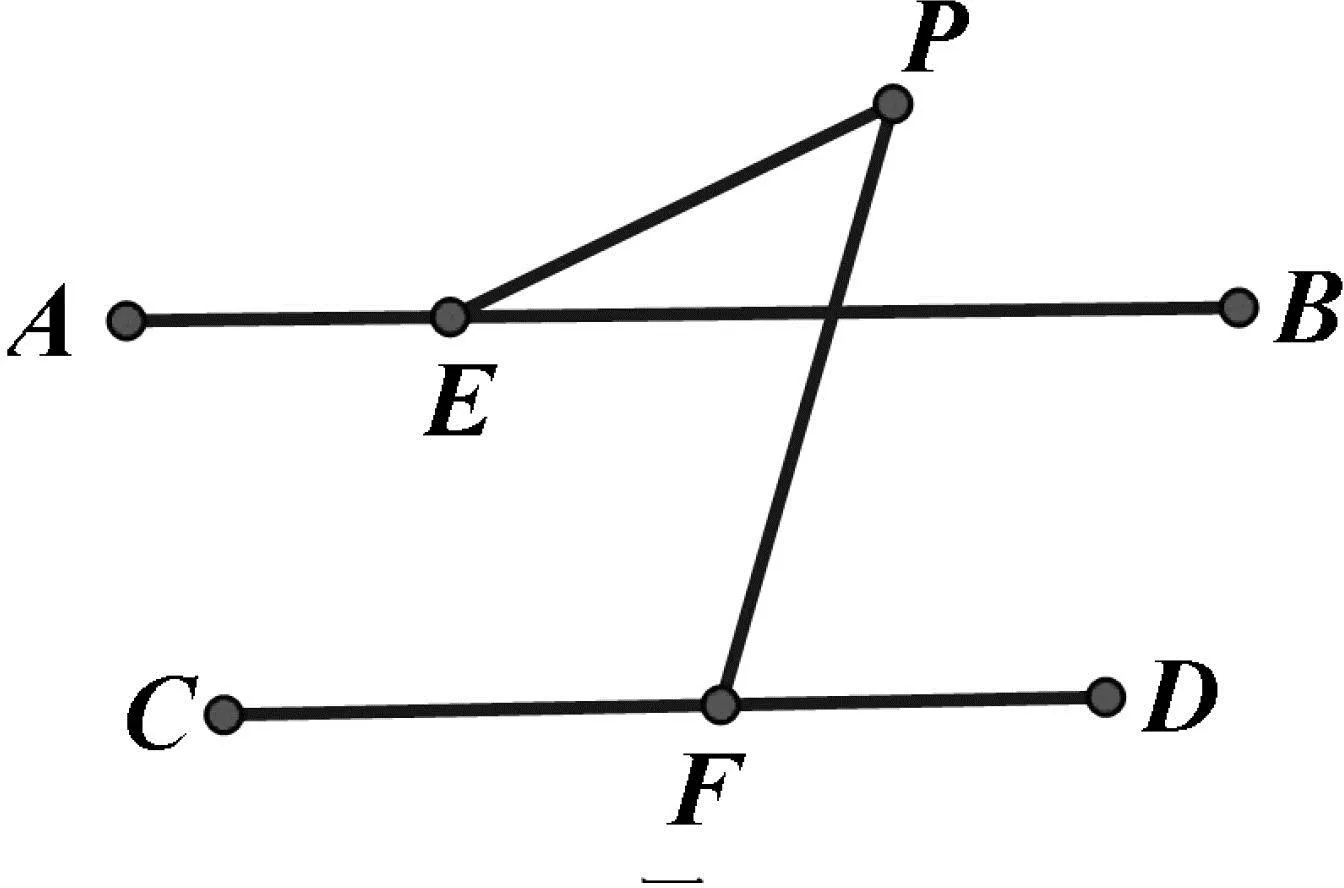
图6

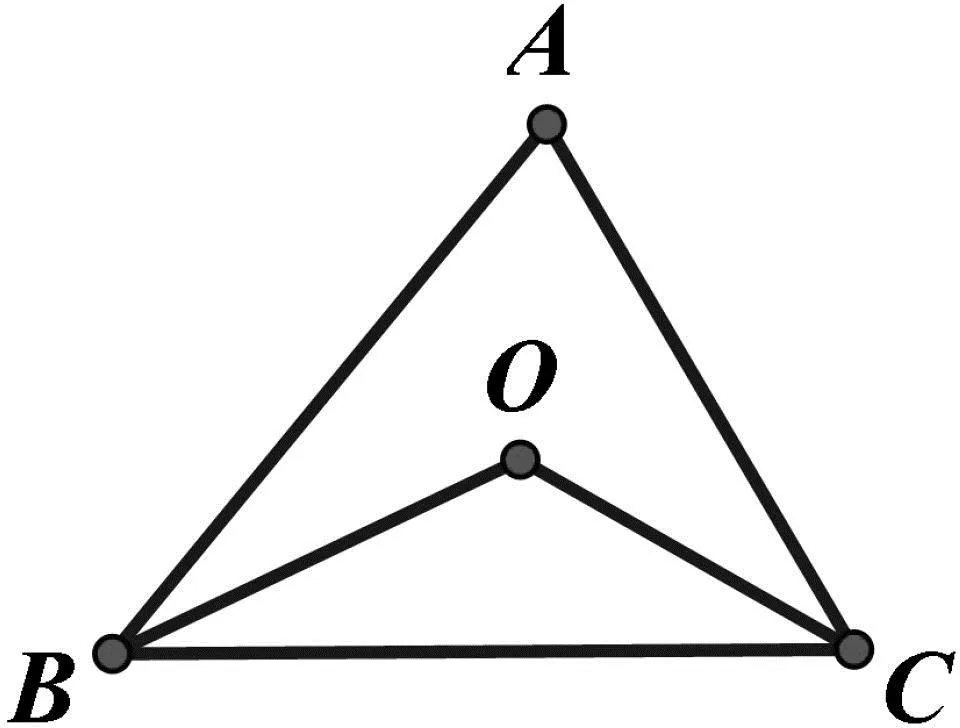
图7

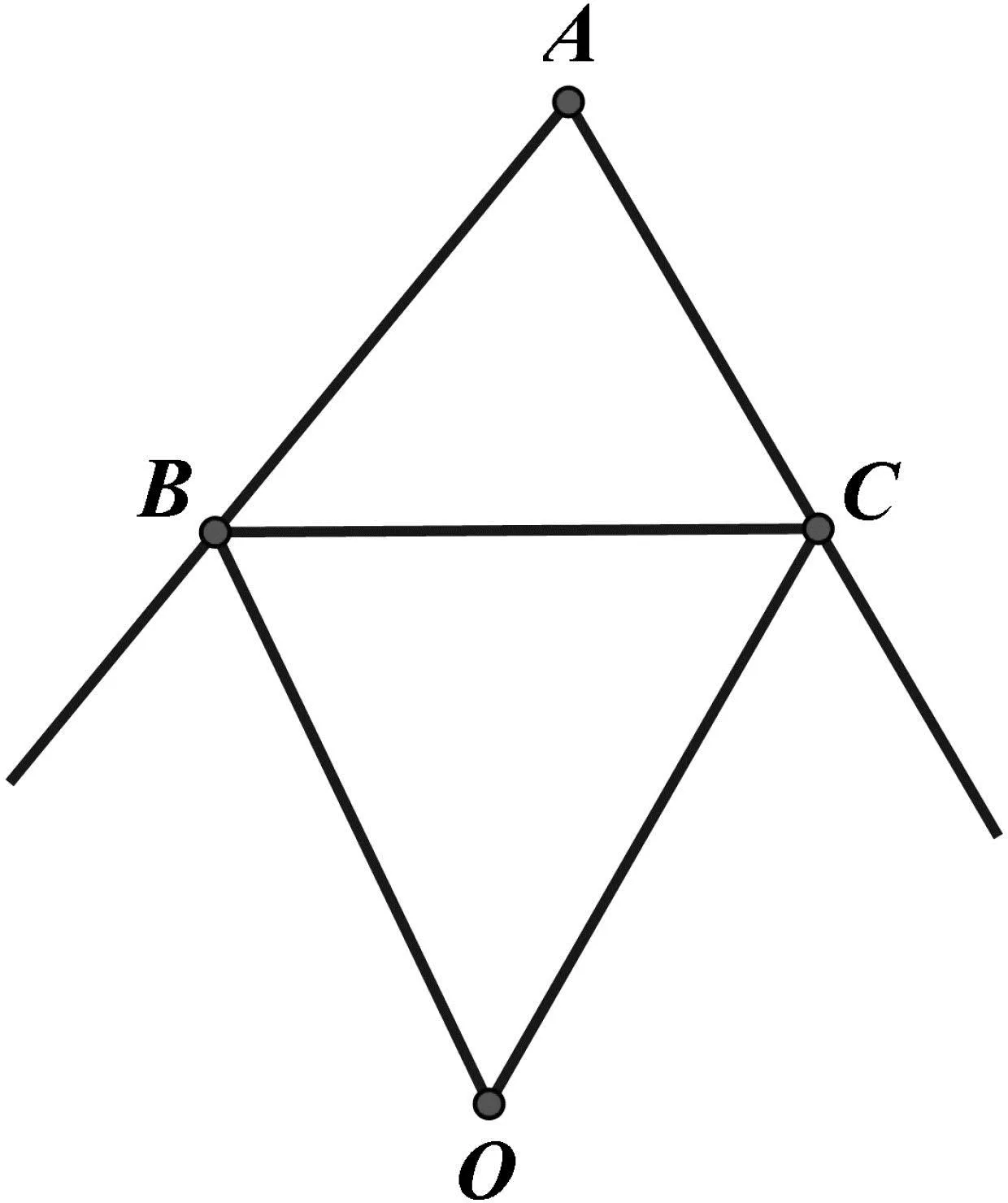
图8

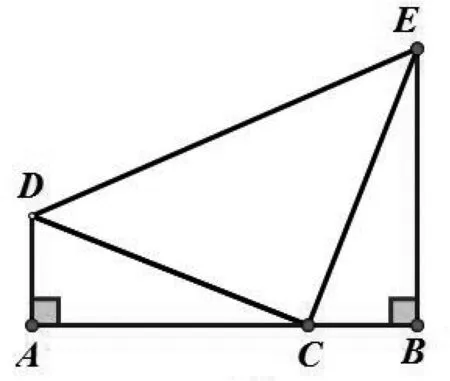
图9

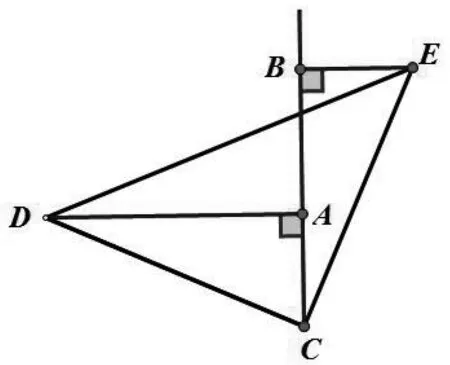
图10

例6 把△ABC的纸片沿DE折叠.(1)如图11,若点A落在四边形BCDE内部点A'的位置,请探究∠A'、∠1、∠2的数量关系;(2)如图12,若点A落在四边形BCDE内部点A'的位置,请探究∠A'、∠1、∠2的数量关系.

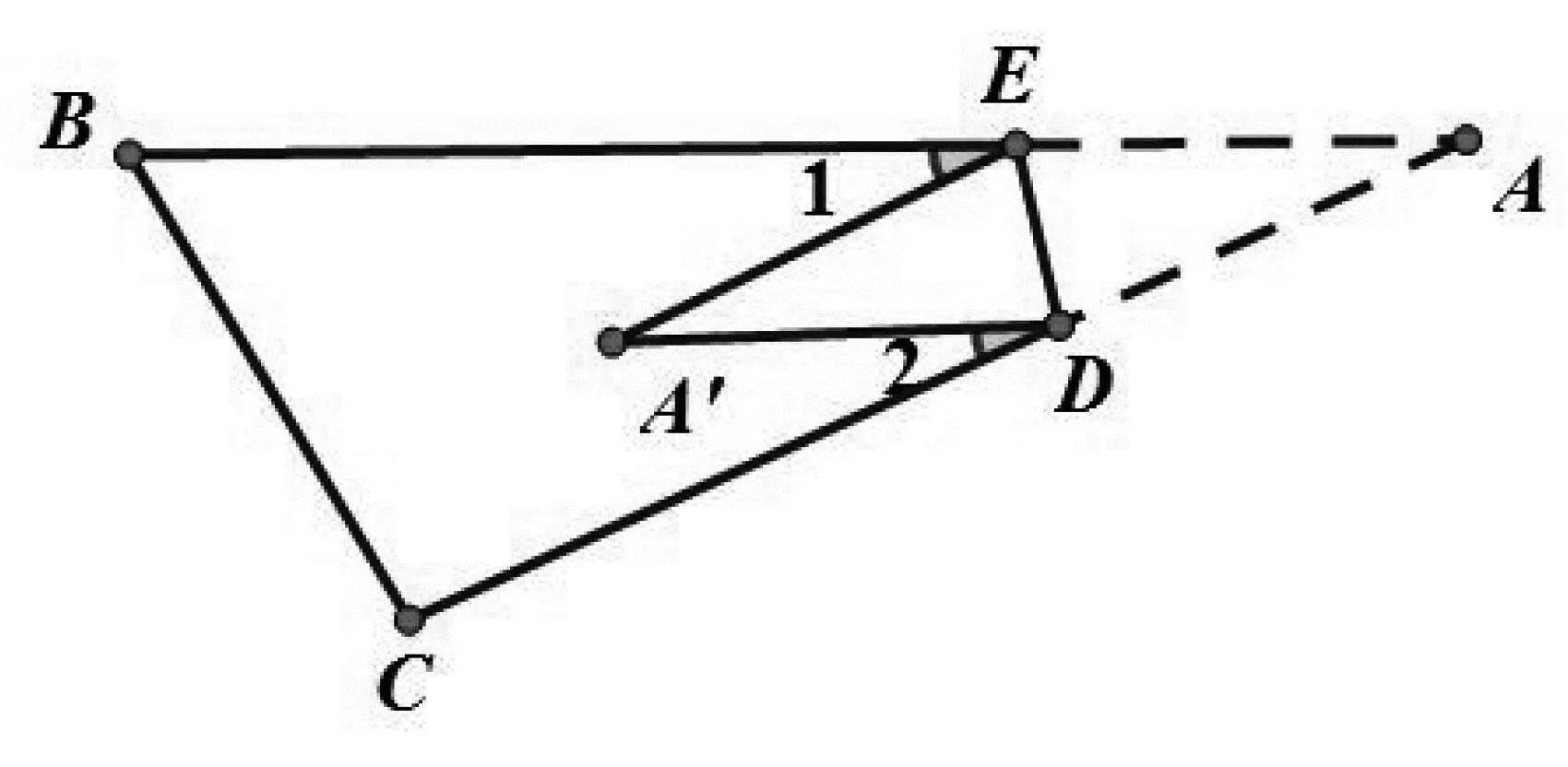
图11

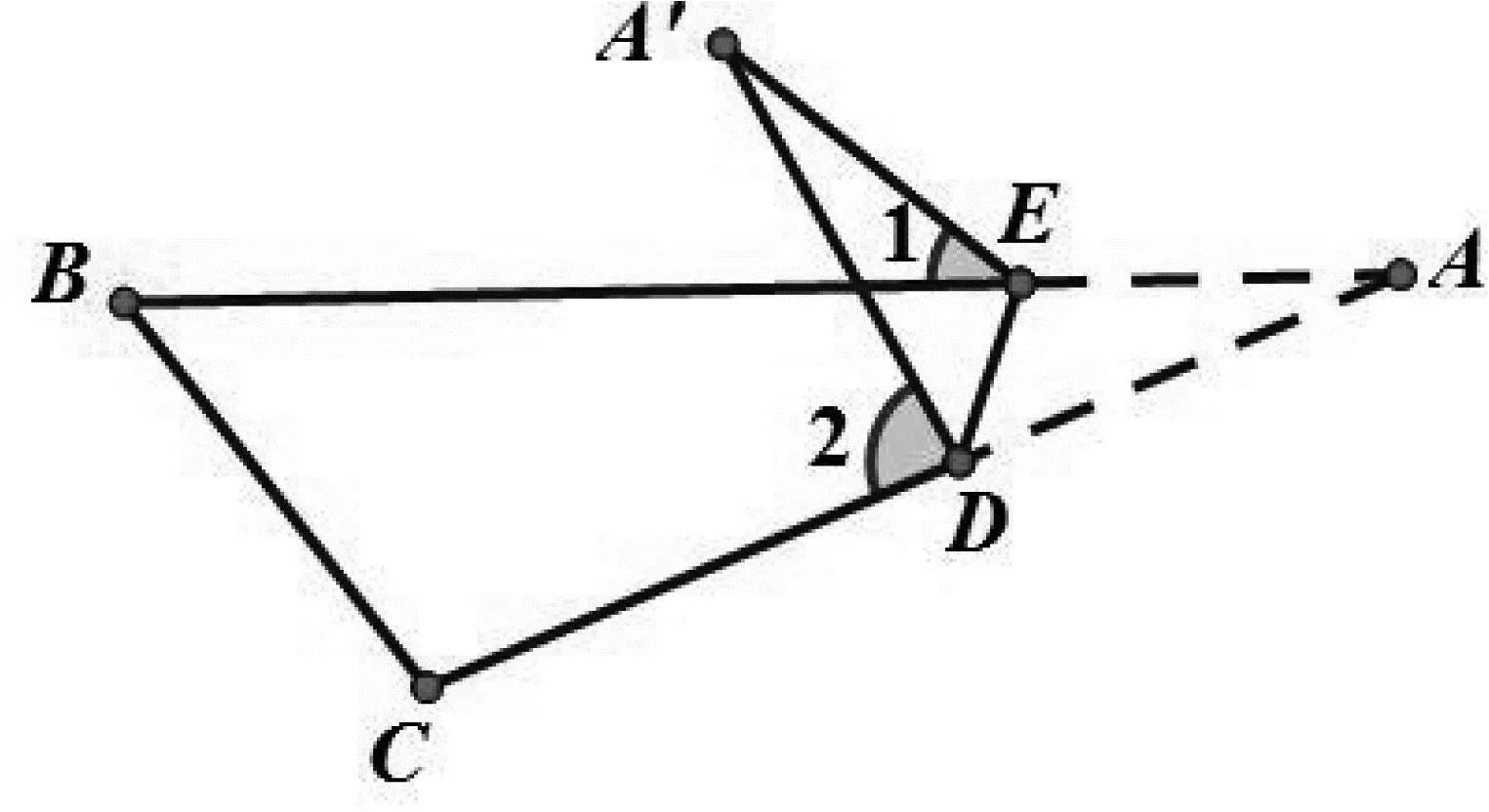
图12

在以上两例的问题探究中,学生又能进一步体会到“形内外”与“正负性”的“异曲同工”中的“美观”;“殊途同归”中的“美好”;“一脉相承”中的“美妙”.这正是数学学习的真谛.实际上,学习就是培养学生的“学习力”.这正是学生所需要的,也是我们社会所需要的.

结语：真正有价值的教育,是让学生透彻理解那些普遍原理,这些原理适用于各种不同的具体事例.只有让学生摆脱教科书,忘记那些为考试背熟的细节,这时学到的知识才有价值.这也正是透过知识的“生长力”,让学生感受真正“生长的意义”.