回归教材溯源 倡导“一题多变”——以一道全国高考真题为例

张国林

云南省玉溪第一中学 (653100)

数列是《普通高中数学课课程标准(2017年版2020年修订)》选择性必修课程中函数主线的重要内容之一,也是历年高考数学试卷中的主干知识之一．每年高考中,数列模块知识都是一个重要命题点,除了数列自身的概念、公式、性质等的考查外,还经常合理融合函数与方程、不等式等其他相关知识,也是高考命题中考查“四基”,以及数学抽象、数学运算、逻辑推理等核心素养,成为考查创新意识与创新应用的一个重要的风向标,倍受各方关注．

1．真题呈现

(2023年高考数学全国乙卷文科·18)记Sn为等差数列{an}的前n项和,已知a2=11,S10=40．

(1)求{an}的通项公式;

(2)求数列{|an|}的前n项和Tn．

2．思维流程

求解数列的综合应用问题时,其基本策略就是“归”字当头,其思维流程可表示为:

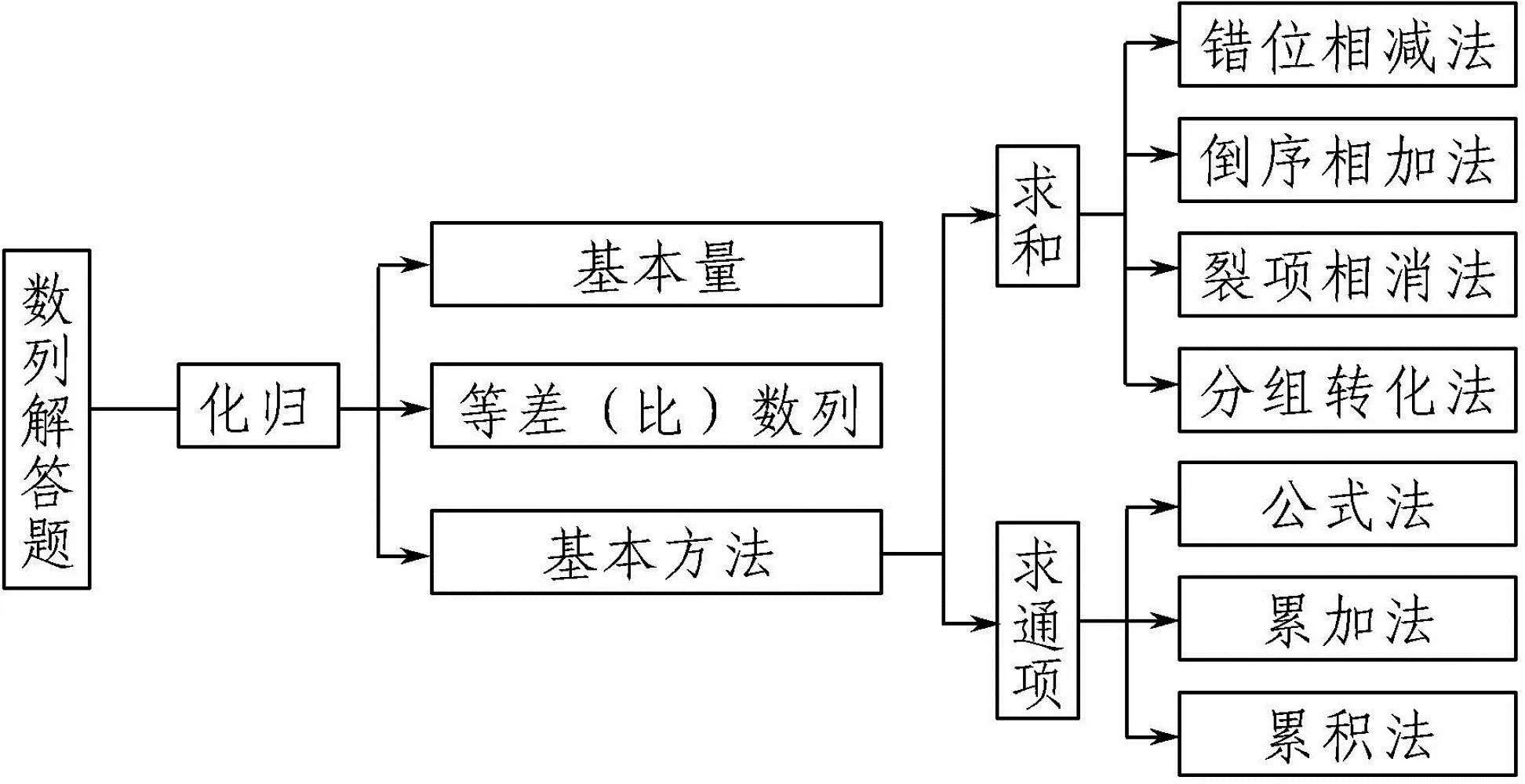
图1

数列问题的化归与归纳,从问题场景入手,对于非特殊数列(非等差或等比数列),往往从特殊情景出发,寻找数列的规律性(周期性、单调性等),归纳出一般性的方法、规律;对于特殊数列,往往将已知数列化归为熟知、确定的等差(比)数列,然后借助数列的概念、性质或基本量运算等来求解;对于应用型数列,往往合理构建数学模型,借助抽象特殊数列的构建,通过数列知识来化归与转化,并结合实际应用场景来综合等．

3．真题破解

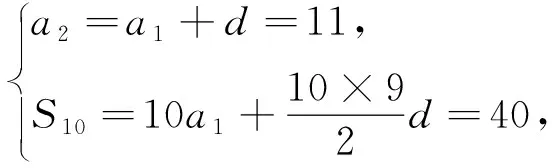
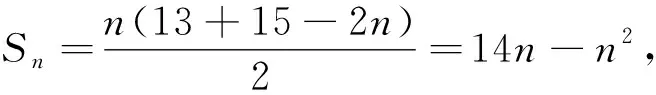
综上所述,数列{|an|}的前n项和

解后反思：借助分类讨论思想来确定不同条件下数列求和公式的表达式,利用“分段函数”形式来表示,是本题的一大亮点．回归数列的函数性,通过“分段函数”形式来表示题设条件或所求结论,成为高考中数列模块知识考查的一个新特点,很好体现高考“在知识点交汇处命题”的指导方针,要引起高度重视．

4．追根溯源

此题可溯源到人教社2019年《数学》(选择性必修第二册)第四章《数列》第23页中的例9,即:已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,则Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由．

所以高考真题脱胎于该例题,将以首项为正数,公差为负数的等差数列来创设问题场景,通过前n项和Sn来综合与应用．这也为该命题的应用,以及高考真题的变式与拓展开拓更加合理的空间．

5．变式拓展

若保留题设场景以及原有的特殊数列,从二次函数视角入手来研究数列前n项和的最值问题,属于简单的数列应用问题．可得以下变式:

变式1 记Sn为等差数列{an}的前n项和,已知a2=11,S10=40．(1)求{an}的通项公式;(2)求数列{an}的前n项和Sn的最大值．

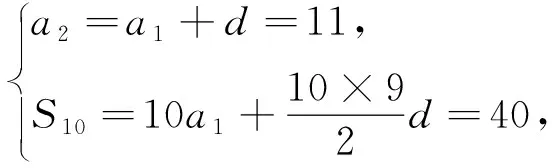
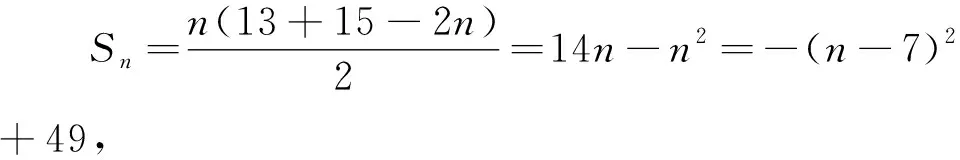
若保留题设场景以及原有的特殊数列,借助指数幂(-1)n的乘积来创设新数列,利用奇、偶项的分类讨论与应用,进而确定与新数列相关的前n项和问题．可得以下变式:

变式2 记Sn为等差数列{an}的前n项和,已知a2=11,S10=40．(1)求{an}的通项公式;(2)令bn=(-1)n·an,求数列{bn}的前n项和Tn．

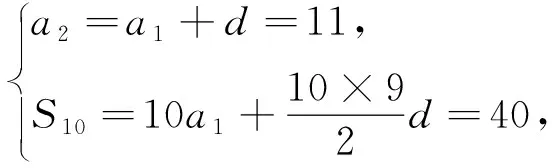
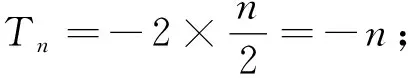
综上所述,数列{bn}的前n项和

若保留题设场景以及原有的特殊数列,借助通项的代数式变化来创设新数列,利用裂项法思维,进而确定与新数列相关的前n项和问题．可得以下变式:

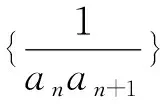
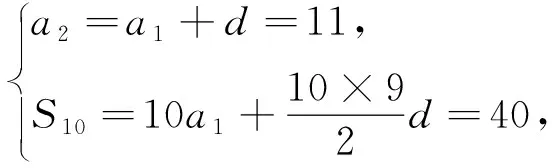
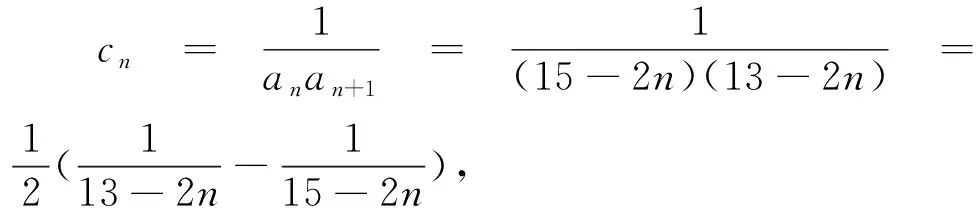
6．教学启示

6.1 回归数学教材,挖掘问题本源

在实际的数学教学与复习备考中,一定要回归高中数学教材,挖掘课本中基本知识点、例(习)题的本源与实质,细细体会高中数学概念的重要性,知识融会贯通的必要性,数学思想方法应用的类比性,数学核心素养参透的关键性等．

在数学教学与学习时,合理引导学生自主学习,挖掘问题的本源,合理把握定义,化归转化问题,借助已有知识来解决新问题,从而才能正确提升学生的知识应用、自主学习等方面的能力,以及提高学生独立思考、独立解决问题的能力．

6.2 倡导“一题多变”,实现“一题多得”

借助一些典型例题,特别是高考真题的“一题多变”,合理发散思维,基于一个典型问题出发,从不同思维视角来挖掘问题的内涵以及知识的联系,全面提升各方面的能力．

而深入进行典型实例的“一题多变”,可以巧妙实现问题的“一题多得”,在聚合数学思维的基础上加以开拓,特别在变式过程中寻找通法,在探究中升华能力,研究之路定会越铺越远,创新意识与创新能力也会得以一定程度的培养与提升．