基于SVD-K-means算法的软扩频信号伪码序列盲估计

张慧芝, 张天骐, 方 蓉, 罗庆予

(重庆邮电大学通信与信息工程学院, 重庆 400065)

0 引 言

直接序列扩频信号因为其隐蔽性、抗干扰、保密性高等优点,在军事和民用通信中被广泛应用[1]。但是传统直接序列扩频技术存在占用带宽大、信息传输效率低等问题。为了解决这些问题,软扩频技术[2-3]将直接序列扩频技术与编码技术相结合,发展成为一种新型的基带扩频技术,相比直接序列扩频信号更难被拦截[4]。现如今,软扩频技术已被广泛应用,如美军的联合战术信息分配系统(joint tactical information distribution system,JTIDS)采用了(32,5)的软扩频通信技术[2];挪威新一代战地通信网提出采用(256,8)和(32,7)的正交矩阵编码[2];宽带码分多址(wideband code division multiple access,WCDMA)也应用了(64,6)的Walsh码软扩频编码技术[5]。

与直扩信号相比,软扩频信号不仅需要估计伪码序列,还需要估计伪码序列规模数,常规估计方法如矩阵分解法[6-7]、最小二乘法[8]、三阶相关函数法[9-10]等将不再适用。目前,关于软扩频信号伪码序列盲估计的研究还较少。文献[11]提出基于相关性的多进制扩频序列盲估计算法,在信噪比(signal to noise ratio, SNR)大于-1 dB时误码率有所减小,但是低信噪比时性能反而更差。文献[12]利用传统K-means聚类实现对伪码序列的估计。但是该方法随机选取聚类初始点,对估计结果影响较大。文献[13]提出一种改进的K-means方法。该方法根据相似度最小准则选取数据对象作为初始聚类点,克服了K-means算法容易陷入局部最优的问题。但是该文采用平均轮廓系数来完成伪码集合规模数的估计,需要多次聚类,计算量较大。文献[14]提出一种改进的近邻传播算法实现了软扩频盲解扩。该方法不用事先指定聚类数目,复杂度低,但是误码率较高。文献[15]在传统密度峰聚类算法的基础上进行了改进,将赋权欧氏距离作为相似性度量指标。该方法可以自动确定截断距离,但是在低信噪比情况下准确度低。

针对上述问题,本文提出一种基于奇异值分解(singular value decomposition, SVD)和K-means聚类相结合的软扩频伪码序列盲估计方法。首先,将接收信号按照一倍伪码周期进行分段,组成观测矩阵后进行SVD,取较大特征值个数作为伪码序列规模数k的估计值并且进行降噪处理。然后,构建相似性矩阵,并对其再次进行SVD,将右奇异矩阵前k行向量,与前k个特征值对应相乘构成判断矩阵。按照判断矩阵绝对值最大原则将数据进行粗分类,并取每个类簇的平均值作为初始聚类中心。最后,通过K-means算法优化分类结果,完成对伪码序列的估计。实验结果表明,该算法能够在较低信噪比下盲估计出软扩频信号的伪码序列,并且与文献[14]相比,本文误码率下降了6%。

1 软扩频信号模型

软扩频信号发射端模型如图1所示。输入信号d(t)先由串/并转换得到k比特的并行数据,每组信息码的状态有M=2k种。再从M条伪码序列中,根据每组信息码的状态选择对应的伪码序列,将信息传递出去。

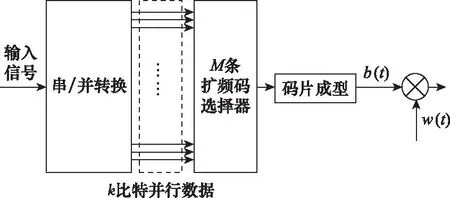
图1 软扩频信号发射端模型Fig.1 Soft spread spectrum signal transmitter model

设M条长度为N的伪码序列表示为

(1)

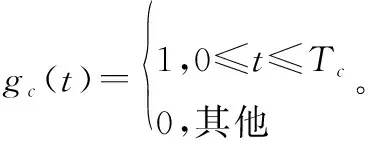
设传输的信息数据为

(2)

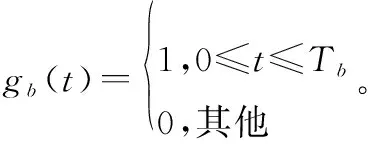
将信息码元每k比特分为一组,则d(t)可以表示为

(3)

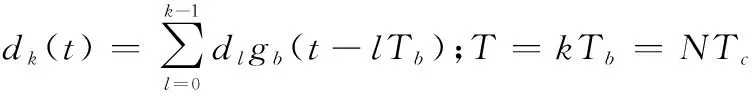
k比特信息码元的权值为

(4)

k比特信息码元选择伪码序列,依据的是权值j。则扩展后的伪码序列表示为

(5)

式中:cj下标由式(4)决定。当通过高斯白噪声信道后,接收到的软扩频信号可以表示为

(6)

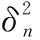
假设伪码速率Tc和伪码周期T=NTc已经估计出来[16],以Tc为采样速率对接收信号进行采样,得到离散的信号:

x(n)=b(t-τ)+w(t)|t=nTc=b(nTc-τ)+w(nTc)

(7)

式中:τ表示延时时间,τ∈[0,N-1],可以使用文献[10]中的方法估计出来。

把采样后的离散序列同步后以伪码序列周期NTc连续分段,每个序列含有N个采样值,即

xi=bi+ni=[x(iN-N),x(iN-N+1),…,x(iN-1)]

(8)

式中:i=1,2,…,Nd;Nd表示总的样本数目。则采样后的数据矩阵为X=[x1,x2,…,xNd]T。

在非合作通信条件下,由于伪码序列规模数不一定与伪码序列长度相等,在已知伪码周期的前提下,若想得到截获信号中的有用信息,需要先估计出伪码集合规模数M和M条伪码序列集合C={c1(t),c2(t),…,cM(t)}。

2 SVD

SVD可以适用于任意矩阵A,其定义如下:

A=UΣVT

(9)

式中:(·)T表示向量的转置。若A是m×n的矩阵,则U是m×m阶酉矩阵,Σ是m×n阶对角矩阵,由A唯一确定,VT是n×n阶酉矩阵[17]。

SVD有以下特性:

(1) 矩阵A的非零奇异值个数等于它的秩。

(2) 矩阵A在噪声干扰后的奇异值变化较小,具有稳定性。

(3) 矩阵A进行归一化处理后不会影响奇异值的相对大小。

2.1 软扩频信号伪码集合规模数的估计

本文根据SVD的特性,对伪码序列规模数进行估计。如果忽略噪声影响,此时rank(X)=M,X有M个奇异值明显大于0,其余奇异值几乎为0。当考虑噪声时,X仍然存在M个奇异值幅值较大,但是其余奇异值受噪声影响幅值会相对增大。因此,软扩频信号伪码序列规模数是X的较大奇异值个数。

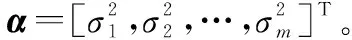
r=[r1,r2,…,rm]T

(10)

ri=var[α(i:m)],i=1,2,…,m

(11)

(12)

(13)

式中:var[·]表示向量的方差;α(i:m)表示α后m-i+1个元素构成的向量子集。向量r′将奇异值之间的差距拉大,下面使用仿真实验进行直观对比。

伪码序列使用gold序列生成,长度取N=127 chip,信息码元按k=4,即M=16分为一组,SNR为-10 dB,样本数目选为Nd=1 000组。生成数据矩阵后进行SVD,对奇异值进行差异放大处理前后对比如图2所示。

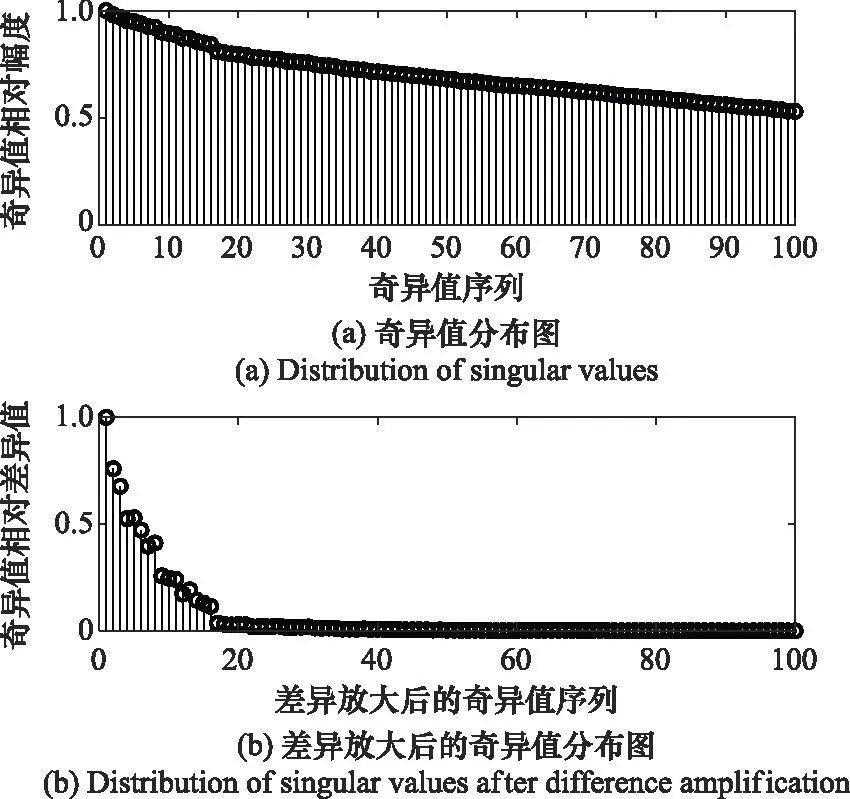
图2 差异放大前后奇异值对比Fig.2 Comparison of singular values before and after difference amplification

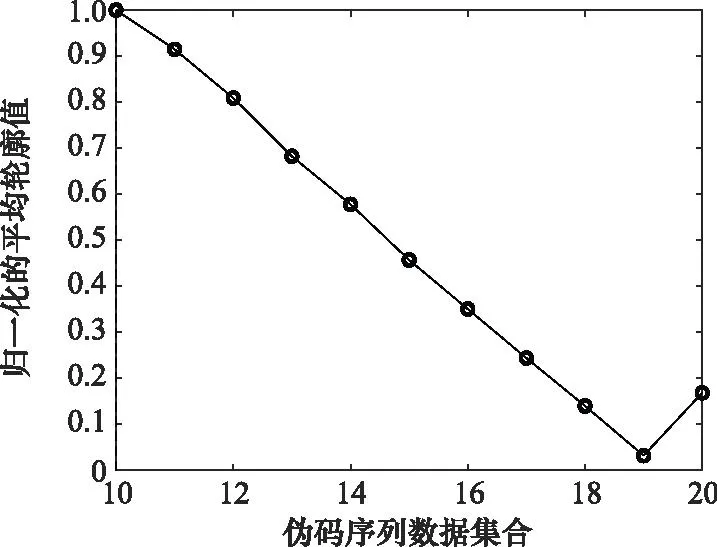
图3 伪码序列集合规模数估计Fig.3 Estimation of the set size number of pseudo code sequences

2.2 基于SVD的降噪过程

由第2.1节分析可知,X的前M个大幅值奇异值包含了X的大部分信息。因此,剔除较小的奇异值,不会损失太多原始信号的特征,反而会减小噪声等干扰对信号的影响,实现降噪效果。

(14)

3 软扩频信号伪码序列估计

3.1 初始聚类中心的确定

对于向量xi和xj,其向量夹角的余弦值大小可以表征它们的相似性程度[20],即

(15)

式中:αi,j表示向量xi和xj的夹角值;cosαi,j∈[-1,1]表示两个向量的夹角余弦值。当cosαi,j=0时,表示向量xi与xj正交;当cosαi,j=±1时,表示向量xi与xj平行。

任取矩阵X′中任意两段数据向量,令rij=cosαi,j,代入式(15)可得

(16)

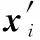
当不考虑噪声且伪码序列之间完全正交时,

(17)

从式(17)可以看出,夹角余弦值可以表示伪码序列的相似度,其数值愈大,表示两个向量的相似度愈高。因此,本文采用夹角余弦值作为相似性的衡量标准,构建相似性矩阵R。

对R进行SVD:

(18)

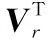
(19)

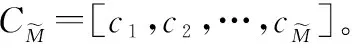
3.2 伪码序列估计

本文在第3.1节中完成了对数据的粗分类。在此基础上,使用K-means算法对分类结果进行优化。SVD-K-means算法的具体步骤如下:

步骤 1对接收信号进行采样、分段,构造输入数据矩阵X。

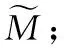
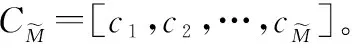
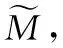
步骤 5令iter=iter+1,计算X′中每个数据对象与聚类中心的相似性,即:

(20)

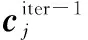
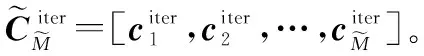
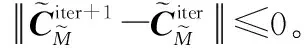
4 仿真实验及结果分析

为了验证本文算法的有效性以及稳定性,本节采用MATLAB进行仿真实验,其中实验1、实验3～7中每一个SNR下进行蒙特卡罗仿真实验次数均为300次。

本文实验主要针对二进制相移键控(binary phase shift keying,BPSK)调制下的软扩频信号。噪声选取高斯白噪声,各项性能指标定义如下。

(1) 误码率

(21)

式中:nl表示第l次蒙特卡罗仿真实验中错误估计的伪码码元数;k表示信息码元每组比特数;N为伪码序列长度。

(2) SNR

(22)

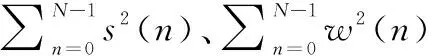
实验 1验证本文算法对软扩频信号的伪码序列集合规模数估计的有效性。

伪码序列使用gold序列生成,长度取N=127 chip,SNR=-20 dB,在不同k值和样本数目Nd情况下,将数据分段后估计伪码集合规模数,不同估计值所占比例如图4所示。

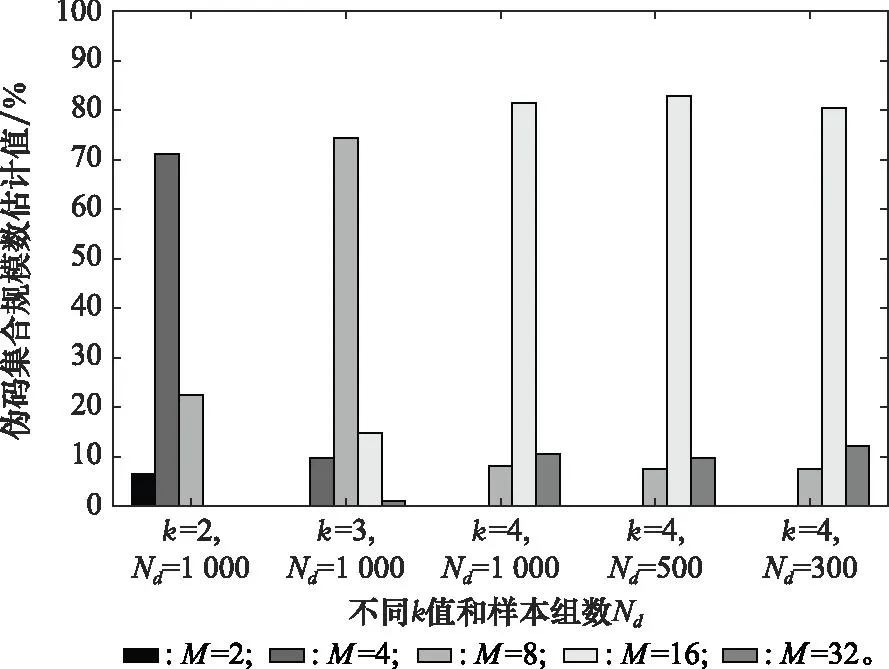
图4 伪码序列集合规模数估计Fig.4 Estimation of the size of pseudo code sequence set

由图4可得,不同k值对应的估计值最高频数都是2k,并且样本数目的选取对估计结果影响较小。因此,本文可以准确估计出伪码序列集合规模数。当SNR≥-20 dB时,该结果不会对后面伪码序列估计产生影响。

实验 2验证本文算法对软扩频信号伪码序列估计的有效性。

伪码序列使用gold序列生成,长度取N=127 chip,信息码元按k=2,即M=4分为一组,SNR=-10 dB,样本数目选为Nd=1 000组。仿真结果如图5所示。

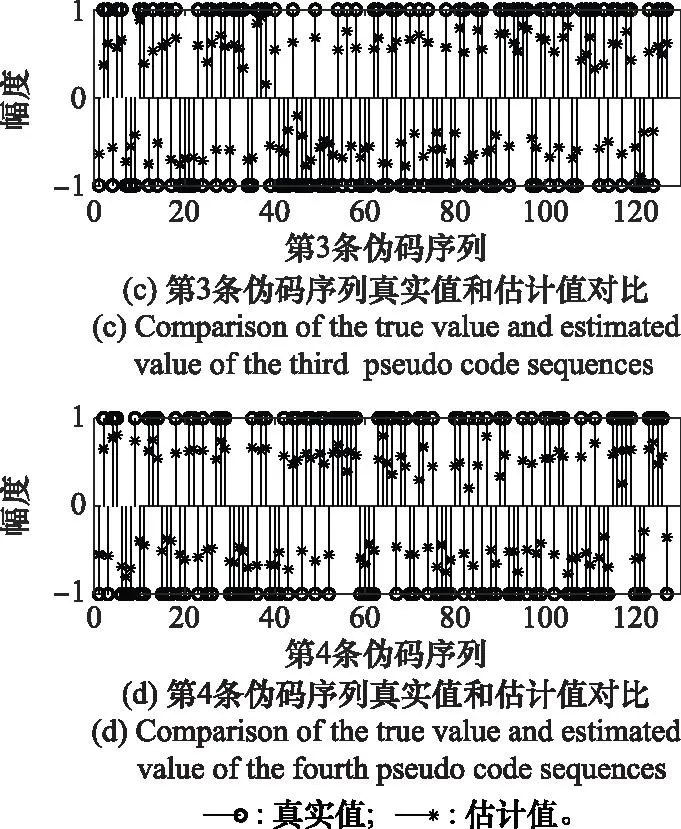
图5 伪码序列真实值与估计值对比Fig.5 Comparison of true value and estimated value of pseudo code sequences

由图5可知,伪码序列估计值的符号和真实值完全相同。因此,本文算法可以准确估计出伪码序列。

实验 3检验伪码序列码型不同对软扩频信号伪码序列估计性能的影响。

伪码序列分别使用m序列、gold序列、Walsh码序列生成,长度取N=127 chip,样本数目为Nd=1 000组,信息码元按k=2分为一组进行对比仿真实验。软扩频信号伪码序列估计的误码率如图6所示。

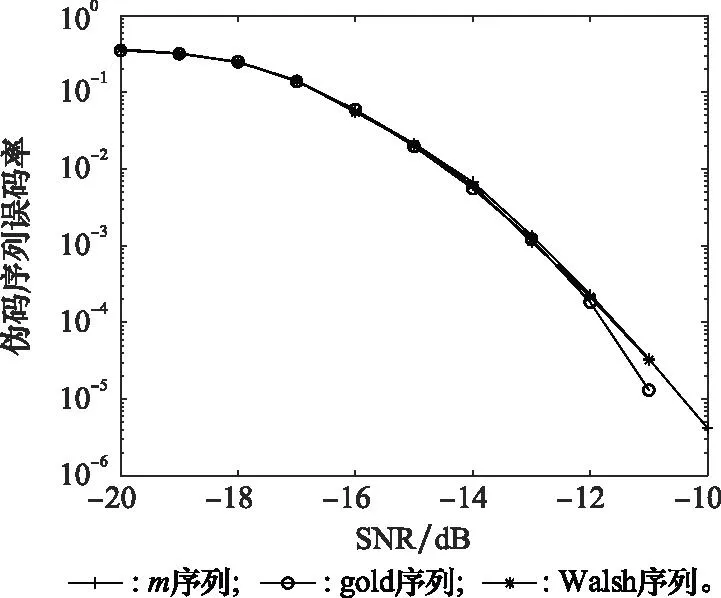
图6 不同码型下伪码序列估计误码率Fig.6 Error rate estimation for pseudo code sequences with different code types

由图6可得,随着SNR的下降,误码率不断增加,而不同码型下伪码序列估计误码率相差不大。因此,不同伪随机码对本文算法的结果影响不大。

实验 4检验信息码元每组比特数k对软扩频信号伪码序列估计性能的影响。

伪码序列使用gold序列生成,长度取N=127 chip,样本数目为Nd=1 000组,信息码元分别按k=2,3,4分为一组进行对比仿真实验。软扩频信号伪码序列估计的误码率如图7所示。

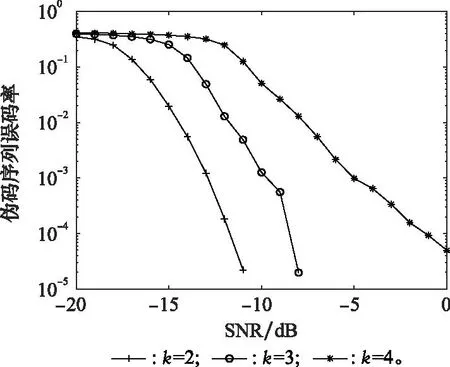
图7 不同k值下伪码序列估计误码率Fig.7 Error rate estimation for pseudo code sequences with different k values

由图7可得,在信息码元分组不同的情况下,随着SNR的增加,伪码序列估计的误码率都在下降;并且在相同的SNR下,误码率随着k值的增大而不断增大。这是因为在其他条件相同的情况下,随着伪码序列集合规模数的增大,属于同一伪码序列的数据组数相对减少,相互之间的干扰也随之增大,判断错误的概率就不断增加。

对于高SNR但是k较大时,可以在粗分类后进行二次分类,根据相似度将受噪声影响较大的数据对象去除,再求初始簇中心,进一步减小误码率,避免误码率无法降到0的情况出现。

实验 5检验伪码序列长度对软扩频信号伪码序列估计性能的影响。

伪码序列使用gold序列生成,样本数目为Nd=1 000组,信息码元按k=2分为一组,长度分别取N=127 chip,255 chip,511 chip进行对比仿真实验。不同伪码序列长度下伪码序列估计的误码率如图8所示。

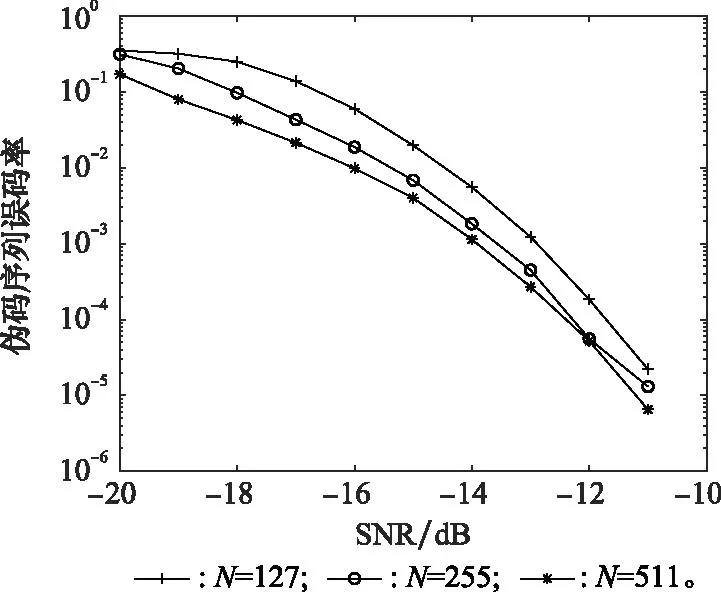
图8 不同伪码序列长度下伪码序列估计误码率Fig.8 Error rate estimation for pseudo code sequence with different lengths of pseudo code sequence

由图8可知,在伪码序列长度不同的情况下,随着SNR的增加,伪码序列的估计误码率全部降低;并且随着伪码序列长度的增加,在相同SNR下误码率也在不断降低。这是因为在其他条件相同的情况下,抗干扰容限会随着伪码序列长度的增加而不断增加,从而导致误码率不断下降。

实验 6检验不同样本数目下对软扩频信号伪码序列估计性能的影响。

伪码序列使用gold序列生成,长度取N=127 chip,样本数目分别为Nd=1 000,500,300组,信息码元按k=2分为一组进行对比仿真实验。不同样本数目下伪码序列估计的误码率如图9所示。

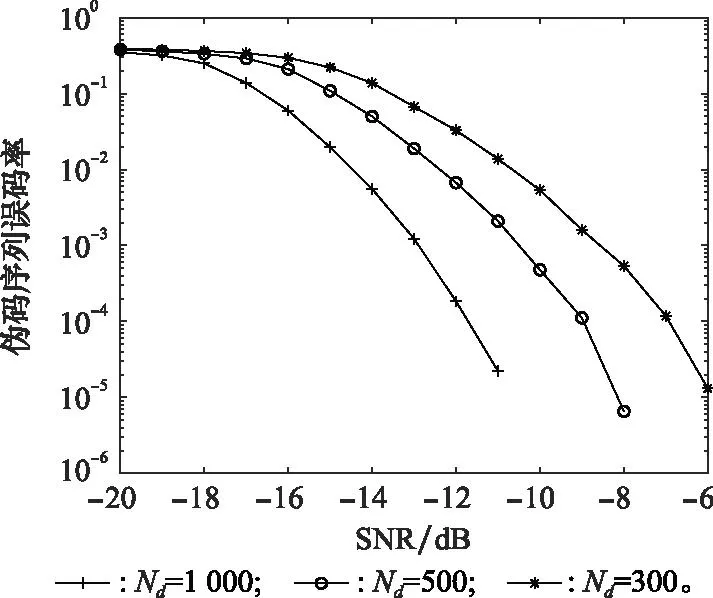
图9 不同样本数目下伪码序列估计误码率Fig.9 Error rate estimation of pseudo code sequences under different sample numbers

由图9可得,伪码序列估计的误码率在样本数目不同的情况下,均随SNR升高而降低;并且在相同的SNR下,随着样本数目的减少,误码率也越来越高。因此,通过增加样本数目,可以提高本文算法的性能。

实验 7比较不同算法对软扩频信号伪码序列估计的性能。

使用Walsh码生成伪码序列,长度取N=128 chip,样本数目为Nd=400组,信息码元按k=2分为一组,分别使用本文算法、改进的K-means算法[13]和改进近邻传播算法[14]进行对比仿真实验。不同算法的伪码序列估计误码率如图10所示。

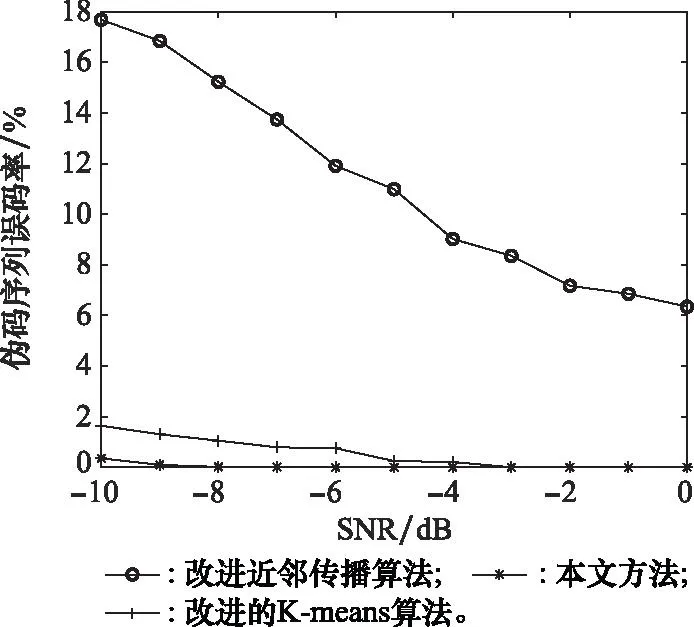
图10 不同算法伪码序列估计误码率对比Fig.10 Comparison of error rate of pseudo code sequence estimation by different algorithms

由图10可得,在SNR为-10 dB时,本文算法可以将误码率降至0.4%以下,而伪码序列在-9 dB以上时几乎完全估计准确。并且在相同条件下,本文算法性能明显优于基于改进近邻传播算法,与改进K-means算法性能相当,但是改进K-means算法随着搜索次数的增加,计算量有所增大。

5 结 论

针对软扩频信号伪码序列盲估计的问题,本文利用不同伪码序列之间的正交性,提出了SVD与K-means聚类相结合的方法。本文先对数据矩阵进行SVD估计伪码集合规模数、降噪。再根据相似性矩阵的右奇异矩阵进行粗分类,初始聚类中心取同一类簇的平均值。最后,通过K-means算法进行分类优化,得到伪码序列的估计值,并且根据分类结果可以得到信息序列。仿真实验证明了算法的有效性,在SNR-16 dB时仍然可以较为准确估计出伪码序列。相比于文献[13]使用平均轮廓系数进行伪码序列集合规模数估计,本文方法不需要多次聚类,计算量有所减少。与此同时,本文也避免了随机选取初始聚类点造成的结果不稳定的问题。