交替极化阵列对消盲区分析与验证

高宏璋, 葛松虎, 郭 宇,*, 刘 让, 孟 进

(1. 海军工程大学军用电气科学与技术研究所, 湖北 武汉 430033;2. 海军工程大学舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)

0 引 言

在现代化高科技战场中,雷达抗干扰技术在信息“高地”的争夺中发挥着举足轻重的作用。基于极化敏感阵列的空-极化域联合抗干扰技术拥有比单域抗干扰技术更强的抗干扰能力,是当今雷达抗干扰技术的研究热点[1-3]。交替极化阵列是最基础的极化敏感阵列之一。交替极化阵列不仅具有较强的抗干扰能力,而且拥有设备成本低、天线互耦低等优点,具有非常高的实用价值[4-5]。

然而,实战条件下电磁环境异常复杂,干扰信号可能为任意空间来向和任意极化状态。当干扰信号的空域和极化域特征与目标信号相似时,空-极化域联合抗干扰技术在消除干扰的同时也会抑制目标信号,导致干扰对消后信干噪比(signal to interference plus noise ratio, SINR)低于雷达系统需求,从而形成干扰对消盲区,例如极化状态与目标信号近似的主瓣干扰。

为了提高阵列的抗干扰能力,学者们提出了多种行之有效的方法。在空域抗干扰方面,文献[6-8]利用人工蜂群算法、蝙蝠算法等,通过改变阵元间距、阵元数目,优化得到最小峰值旁瓣电平,从而提高了阵列抑制旁瓣干扰的能力;文献[9-12]通过构造互素阵列,得到最大自由度和更大的阵列孔径,从而提高了阵列的抗干扰能力。文献[13-14]设计了一种大孔径辅助阵列,该阵列能够有效提高主瓣干扰下的输出SINR。以上方法通过优化阵元间距、阵元数目等,从不同角度提高了阵列的抗干扰能力,但是改变阵元间距和阵元数目也会影响对消盲区的分布,因此还需考虑优化结果对对消盲区的影响。在极化抗干扰方面,文献[15-19]利用极化域抗干扰技术,通过优化发射极化与接收极化实现抑制干扰、增强目标的方法,从而提高了阵列的抗干扰能力,但是该方法只是通过改变阵列天线的极化状态来规避对消盲区,并不能减小对消盲区的影响。在空-极化域联合抗干扰方面,文献[20-21]研究了共点极化线阵的干扰对消性能,文献[22-23]研究了交替极化阵列的干扰对消性能,文献[24-27]研究了空频极化抗干扰技术和空时极化抗干扰技术的干扰对消性能,这些方法通过多域联合对消提高了阵列抗干扰能力,但在各域上还是存在对消盲区。

为了提高交替极化阵列对消任意空间来向、任意极化状态干扰的能力,本文针对交替阵列对消盲区问题展开研究。本文首先通过建立交替极化阵列对消盲区的空域、极化域和空-极化域模型,推导了对消盲区位置和大小的数学表达式,从而解决了交替极化阵列对消盲区的定量描述问题。然后基于交替极化阵列对消盲区的数学表达式,分析了对消盲区的分布规律与影响因素,发现阵元间距能够显著影响对消盲区的分布,且交替极化阵列对消盲区大于共点极化阵列对消盲区。之后基于对消盲区模型进行了数值仿真,仿真结果验证了理论分析。最后基于信道模拟器搭建了实验验证平台,通过实验证明了理论分析的有效性。

1 交替极化阵列模型与对消盲区模型

1.1 交替极化阵列模型

如图1所示,交替极化阵列由M个阵元组成(M为偶数),阵元间距为d。每个阵元由一个偶极子天线组成,相邻的两个天线极化状态相互正交。令第一个阵元中的天线为主天线,其余天线为辅助天线。

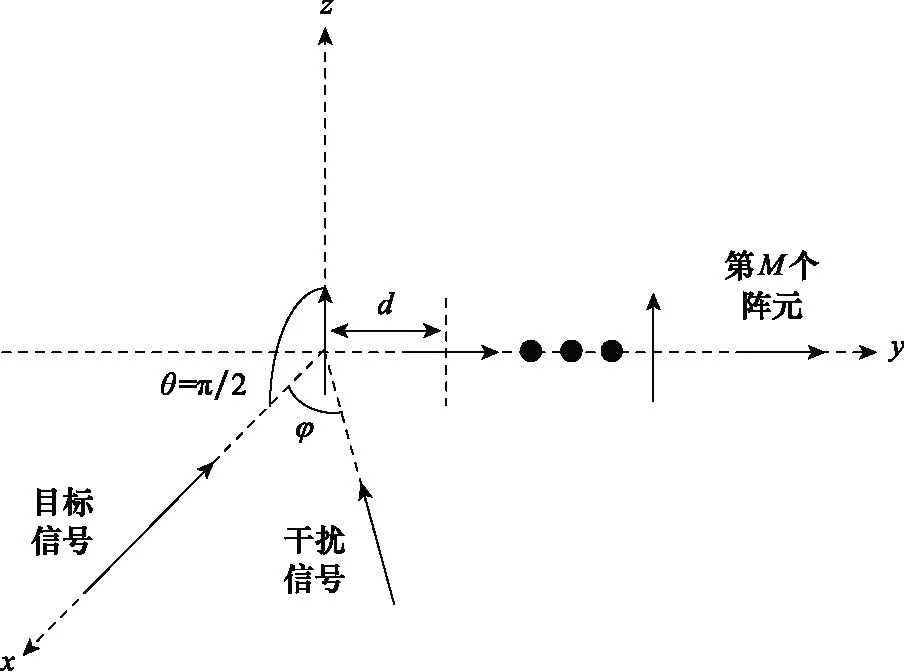
图1 交替极化阵列Fig.1 Alternate polarization array

令目标与干扰都在xoy平面内,即目标信号与干扰信号的俯仰角为θ=π/2。令方位角分别为φs、φi,极化幅角分别为γs、γi,极化相位差分别为φs、φi。令ass为目标空域导向矢量,aps为目标极化域导向矢量,asi为干扰空域导向矢量,api为干扰极化域导向矢量,则有:

(1)

令as为目标信号空-极化域导向矢量,ai为干扰信号空-极化域导向矢量,则有:

(2)

式中:⊗为Hadamark积。当期望信号方向和协方差矩阵已知,且期望信号与干扰和噪声互不相关时,阵列输出SINR可以表示[5]为

(3)

1.2 交替极化阵列对消盲区模型

雷达系统所需最小信噪比(signal to noise ratio, SNR)为一定值[28],令雷达系统的SNR阈值为χ1,则在干扰背景下,当对消后SINR<χ1时,干扰信号位于对消盲区。假设雷达主波束始终对准目标,发射信号的极化状态为垂直极化,则有φs=0,γs=π/2,φs=0。因为现役雷达大部分采用线极化信号[29],例如美国的AN/SPS-48、AN/SPS-49、AN/SPS-64、AN/APS-134以及AN/APS-145等,所以本文研究了线极化干扰下交替极化阵列的对消盲区。对于圆极化干扰和椭圆极化干扰,还需在本文研究结论上进行扩展,考虑极化相位差引起的对消盲区。

1.2.1 空域对消盲区模型

当只考虑空域对消盲区时,令φi在[-π/2,π/2]内变化,γi=π/2,φi=0。则有:

(4)

将式(4)代入式(3),再结合ρ<χ1得

(5)

式中:β=(1-cos(Mηi))/(1-cos(2ηi));rINR=Pi/Pn;rSNR=Ps/Pn。令盲区判决函数为L,盲区阈值为χ2,空域对消盲区为Bs。由式(5)得到交替极化阵列空域对消盲区模型为

(6)

1.2.2 极化域对消盲区模型

只有当φi位于空域对消盲区时,极化域上才存在对消盲区。因此,当只考虑极化域对消盲区时,令φi位于空域对消盲区,令γi在[-π/2,π/2]内变化,φi=0。则有:

(7)

将式(7)代入式(3),再结合ρ<χ1得

(8)

令极化域对消盲区为Bp。由式(8)得到交替极化阵列极化域对消盲区模型为

(9)

1.2.3 空-极化域对消盲区模型

当考虑空-极化域对消盲区时,令φi、γi在[-π/2,π/2]内变化,φi=0。易得空-极化域对消盲区模型的盲区阈值与极化域对消盲区模型相同,空-极化域对消盲区模型的盲区判决函数L与极化域对消盲区模型相似,区别仅为前者φi未知,后者φi已知。令空-极化域对消盲区为Bsp,则空-极化域对消盲区模型为

(10)

2 交替极化阵列对消盲区分析

2.1 空域对消盲区分析

2.1.1 空域对消盲区模型分析

式(6)给出了空域对消盲区模型,由L(φi)>χ2得

(11)

式(11)中,只有ηi中存在φi,又cos(Mηi)和cos(2ηi)在φi∈[-π/2,π/2]对称,可见空域对消盲区在[-π/2,π/2]对称分布。因为φi只存在于ηi中,因此可由ηi的取值范围得出空域对消盲区的范围。对于式(11),ηi的取值范围为

ηi∈(0,ε)∪(π-ε,π+ε)∪…∪(nπ-ε,nπ+ε)

(12)

式(12)中,n为正整数,ε∈(0,2π/M)且满足式(13):

(13)

由ηi分块分布可知交替极化阵列空域对消盲区由多个子盲区组成。在[0,π/2]上,按照方位角从小到大的顺序,将空域子盲区编号,将子盲区位置用Asn表示,大小用Bsn(n=0,1,2,…)表示,结合ηi=(2πdsinφi)/λ与式(12),得到每个子盲区的位置与大小,并将所有子盲区相加得空域对消盲区Bs,如下所示:

(14)

(15)

(16)

式(14)～式(16)中,n为正整数。由式(14)可知,在[0,π/2]上,空域对消盲区由多个子盲区组成,随着阵元间距d增大,子盲区的个数变多。

为了方便书写,令:

(17)

通过求导可知,Bs0在Q1内保持不变,在Q2内单调递减;Bsn在Q3内单调递增,在Q4内单调递减。Bs在Q5内单调递减;在Q3内单调递增。由此可得,当d=nλ/2-λε/2π时,Bs取极小值。

2.1.2 与共点极化阵列空域对消盲区对比分析

(18)

由式(18)与式(13)易得

(19)

假设ε′≥ε,则有:

(20)

因为式(18)与式(19)矛盾,所以ε′≤ε。由文献[30]可得,共点极化阵列空域对消盲区大小为

(21)

结合式(21)与式(16)可知,在相同条件下,交替极化阵列的空域对消盲区大于共点极化阵列的空域对消盲区。

2.2 极化域对消盲区分析

2.2.1 极化域对消盲区模型分析

式(9)给出了极化域对消盲区模型,由L(d,γi)>χ2得

(22)

因为sin2γi在[-π/2,π/2]对称,所以极化域对消盲区在[-π/2,π/2]对称分布。[0,π/2]内,得到交替极化阵列极化域对消盲区的位置(Ap)与大小(Bp)分别为

(23)

(24)

2.2.2 与共点极化阵列极化域对消盲区对比分析

(25)

因为Bp>0,从而得到式(26)成立:

(26)

因为:

(27)

因此,有:

(28)

2.3 空-极化域对消盲区分析

2.3.1 空-极化域对消盲区模型分析

由第1.2.2节分析可知,只有当干扰信号的方位角φi位于空域对消盲区时,极化域上才存在对消盲区,所以在空域对消盲区内对Bp积分即可得空-极化域对消盲区。在[0,π/2]上,按照方位角从小到大的顺序,将空-极化域子盲区编号并分别用Bspn(n=0,1,2,…)表示,得到每个子盲区的大小,其表达式为

(29)

将所有子盲区相加得到空-极化域对消盲区Bsp,其表达式为

(30)

因为空域对消盲区与极化域对消盲区都在[-π/2,π/2]上对称分布,可见空-极化域对消盲区也对称分布。由式(29)可知,在[0,π/2]上,空-极化域对消盲区由多个子盲区组成且随着阵元间距d增大,子盲区的个数变多。

结合第2.1节与第2.2节,可以联合空域对消盲区位置和极化域对消盲区得位置,得到空-极化域对消盲区位置。

2.3.2 与共点极化阵列空-极化域对消盲区对比分析

由第2.3.1节可知,在空域对消盲区内对Bp积分即可得空-极化域对消盲区,因此空-极化域对消盲区大小Bsp与Bs和Bp呈正相关。

由第2.1和第2.2节可知,相同条件下交替极化阵列的空域对消盲区大于共点极化阵列的对消盲区,且交替极化阵列极化域对消盲区大于共点极化阵列极化域对消盲区。因此,相同条件下,交替极化阵列空-极化域对消盲区大于共点极化阵列空-极化域对消盲区。由此可知,交替极化阵列虽然通过减少天线数目降低了设备成本,但增大了阵列的对消盲区。

3 对消盲区模型的数值仿真与实验验证

数值仿真与实验采用四元交替极化阵列,各参数为λ=0.1 m、χ1=12.6 dB、SNR=20 dB,干噪比(interference to noise ratio, INR)为40 dB。其中λ=0.1 m时,电磁波位于L波段,L波段是远程地对空警戒雷达首选波段[31];χ1=12.6 dB对应的探测概率为0.5,虚警概率为10-8,符合实际应用指标[28];SNR与INR取值同样符合实际情景,需要指出的是,雷达系统能够通过脉冲压缩和脉冲积累提高SNR,而本文侧重于干扰对消技术,因此采用经过脉冲压缩与脉冲积累处理后的SNR。以上参数均在合理范围内,且改变参数不影响实验结论。

3.1 数值仿真

定义空域对消盲区占比为Rs=2Bs/π,极化域对消盲区占比为Rp=2Bp/π,空-极化域对消盲区占比为Rsp=4Bsp/π2。通过数值仿真,得到对消盲区占比,如图2所示。

图2 对消盲区占比示意图Fig.2 Schematic diagram of cancellation blind area proportion

由图2(a)可以看出,交替极化阵列的空域对消盲区占比随阵元间距增加呈现衰减振荡趋势且在d=nλ/2附近存在极大值与极小值,当d=λ/2-λε/2π≈0.45λ时,空域对消盲区占比有最小值Rs=5.6%。

图2(b)给出了d=0.5λ时极化域对消盲区占比。由图可知,当干扰信号的方位角位于空域对消盲区时,极化域对消盲区占比才不为0。

通过微元法求解式(30),得到图2(c)。由图2(c)可以看出,交替极化阵列的空-极化域对消盲区占比同样随阵元间距增加呈现衰减振荡趋势,且在d=nλ/2附近存在极大值与极小值。对比于空域对消盲区,相同间距下空-极化域对消盲区占比更小,证明空-极化域拥有更强的抗干扰性能。在(0,2λ)范围内,d≈0.45λ时,空-极化域对消盲区占比有最小值Rsp=1.06%,而d≈0.54λ时,Rsp=20.41%,可见阵元间距能够显著影响交替极化阵列对消盲区的大小。

将交替极化阵列对消盲区占比与共点极化阵列对消盲区占比对比,如图2所示,交替极化阵列对消盲区占比大于共点极化阵列对消盲区占比。通过以上分析可得,图2与理论分析一致。

为了充分验证前面的分析结论,在空域与空-极化域等间距取适量点,利用判决式L>χ2,得到图3和图4所示的对消盲区分布示意图。由图3可以看出空域对消盲区在[-π/2,π/2]上呈对称分布。图中存在多个黑色/灰色的带状盲区,且阵元间距增大,带状盲区增多,可见空域对消盲区模型的对消盲区由多个子盲区组成,随着阵元间距增大,子盲区数目增多。按照第2.1节中空域对消盲区编号规则进行编号,可见0号盲区先恒等于π/2,而后一直减小,n号盲区先增大,而后一直减小。结合图3和图4可以看出,只有当干扰信号的方位角φi位于空域对消盲区时,才存在极化域对消盲区。图4中各图都以φi=0或γi=0为轴对称,可见空-极化域对消盲区呈对称分布。图4中存在多个黑色/灰色的半椭圆状盲区,且阵元间距增大,盲区增多,由此可见空-极化域对消盲区分布图由多个子盲区组成,随着d增大,子盲区的个数变多。图4(b)中黑色/灰色区域远大于图4(a)与图4(c),说明d=0.5λ时空-极化域对消盲区大于d=0.2λ与d=0.75λ时,符合理论分析。

图3 空域对消盲区分布Fig.3 Blind area distribution of space cancellation

图4 空-极化域对消盲区分布Fig.4 Blind area distribution of space-polarization cancellation

图3和图4同时给出了交替极化阵列对消盲区与共点极化阵列对消盲区。对比两图可得,在该仿真条件下,交替极化阵列的对消盲区更大,且共点极化阵列的对消盲区包含于交替极化阵列的对消盲区。综合以上分析可知,图3和图4符合理论分析。

3.2 实验验证

实验系统组成如图5所示。

图5 实验平台Fig.5 Experimental platform

如图5(a)所示,首先信号和干扰注入到信道模拟器,然后通过信道模拟器对四个信道的信号调幅调相,将信号和干扰分别模拟到所需的空间来向和极化状态,之后在采样模块采集所需的数据样本,最后在电脑上分析数据。实验参数同数值仿真。

如图5(b)所示,实验系统包括信号源、干扰源、信道模拟器、采样模块和电脑。其中,信号源采用型号为SMR20的信号发生器生成1.000 01 GHz正弦波,干扰源采用型号为SMC100A的信号发生器生成0.999 99 GHz正弦波,信道模拟器采用思博伦Vertex信道仿真器,采样模块通过zc706数据板采集数据,采样后在PC端用软件保存数据,利用软件处理数据。目标信号与干扰信号频率错开20 kHz是为了在频谱观察对消效果。

各信道间幅相关系可由信号的空-极化域导向矢量确定。对于四元交替极化阵列,信号的空-极化域导向矢量各元素为

(31)

由式(31)可知,各信道的相位分别为-π、-η、-π-2η、-3η,各信道的幅度分别为sinγ、cosφcosγ、sinγ、cosφcosγ。

由于受线缆损耗不相同,采样模块对各信道采样的幅相不一致等影响,还需对实验数据进行幅相校准。本文用参数为φ=0、γ=π/4、φ=π/2的信号做基准信号。首先通过信道模拟器模拟出该信号,然后对该信号采样,通过校准矩阵,将样本校准到φ=0、γ=π/4,最后用该校准矩阵校准其他信号。各数据默认为校准后的数据。单次实验流程如下:

(1) 采集目标信号。利用信号源产生目标信号,通过信道模拟器调幅调相,使φs=0,γs=π/2,采集目标信号并保存在PC端;

(2) 采集干扰信号。利用信号源产生干扰信号,通过信道模拟器将其调整到所需空间来向与极化状态,采集干扰信号并保存在PC端;

(3) 采集目标与干扰的和信号。同时发射目标信号与干扰信号,并在信道模拟器上对各信道调幅调相,采集目标与干扰的和信号并保存在PC端;

(4) 计算目标信号、干扰信号以及和信号的自相关矩阵Rss、Rii、Rxx;

3.2.1 空域对消盲区实验

在空域对消盲区实验中,控制目标信号与干扰信号都为垂直极化,目标信号方位角φs=0,干扰信号方位角φi在[0,π/2]范围内变化。实验分别测试了阵元间距为0.25λ、0.5λ、0.75λ时的空域对消盲区。

为了保证干扰信号确实为信道模拟器设定的空间来向与极化状态,我们对干扰信号进行波达方向(direction of arrival,DOA)估计,DOA估计的极化幅角恒为π/2,误差极小,方位角误差如图6所示,计算得到当阵元间距为0.25λ、0.5λ、0.75λ时,方位角绝对误差均值分别为0.4°、0.3°、0.08°,误差在允许范围内。为了使实验测得空域对消盲区更准确,在空域对消盲区的理论边界附近增加了方位角的取样点数。

图6 方位角误差Fig.6 Error of azimuth argument

实验数据经过PC端处理,得到干扰信号在不同方位时,对消后SINR,结果如图7所示。在[0,π/2]范围内,我们将图7中的对消盲区与图3中的对消盲区作比较,其结果如表1所示。由表1可知,仿真得到的空域对消盲区与实验得到的空域对消盲区大致吻合。

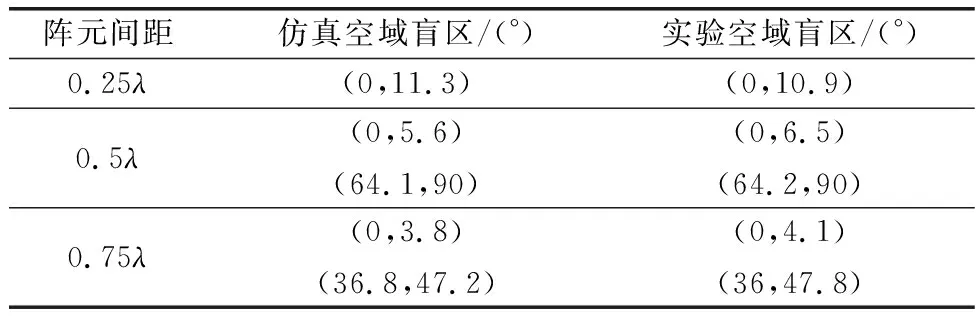
表1 空域对消盲区Table 1 Blind area of space cancellation

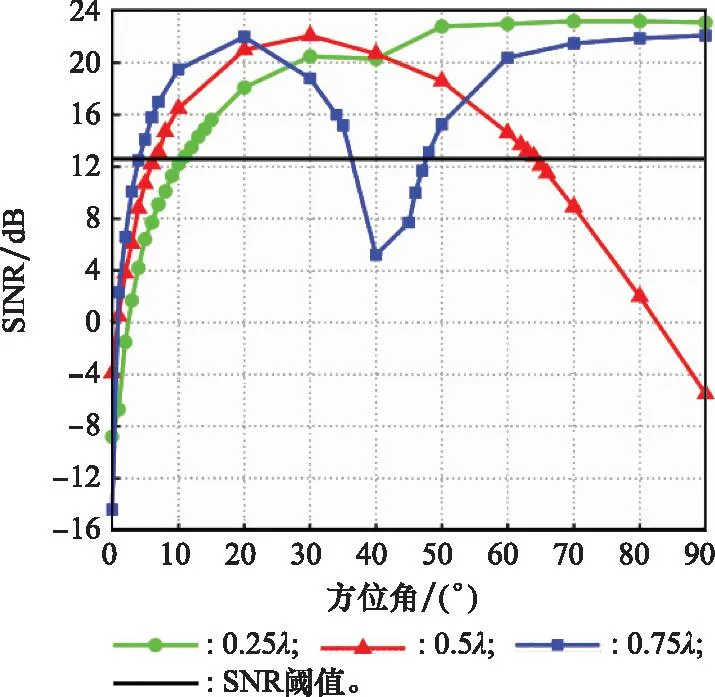
图7 空域对消后SINRFig.7 SINR after space cancellation

经过分析,实验中误差来自于以下几个方面:

(1) 由于采样模块各信道的幅相一致性差,虽然对采样得到得数据进行了校准,但还是存在误差;

(2) 实验中信道模拟器输出功率存在误差,信号传输过程中存在损耗,因此采样模块接收信号的SNR、INR存在误差。

3.2.2 极化域与空-极化域对消盲区实验

在极化域与空-极化域对消盲区实验中,仅抽取部分干扰信号验证分析结论。实验中目标信号与空域对消盲区实验相同。当阵元间距为0.5λ时,令干扰信号方位角分别为0°、30°、70°,测试极化域对消盲区;当阵元间距为0.75λ时,令干扰信号方位角分别为0°、40°、70°,测试极化域对消盲区。为了使实验测得极化域对消盲区更准确,在极化域对消盲区的理论边界附近增加了极化幅角的取样点数。

为了保证干扰信号为信道模拟器设定的空间来向与极化状态,对干扰信号进行DOA估计,DOA估计角度与设定角度之间的误差如图8所示。

由图8可知,方位角与极化幅角绝对误差均值都在1°以内,误差在允许范围内。

实验测得对消后SINR结果如图9所示。在[0,π/2]范围内,将图9中的对消盲区与图4中的对消盲区作比较,其结果如表2所示。由表2可知,在误差允许范围内,这两种途径得到的对消盲区大致吻合。

表2 空-极化域对消盲区Table 2 Blind area of space-polarization cancellation

图9 空-极化域对消后SINRFig.9 SINR after space-polarization cacellation

4 结 论

为了提高交替极化阵列对消任意空间来向、任意极化状态干扰的能力,本文在空域、极化域与空-极化域分别建立了交替极化阵列的对消盲区模型,推导了对消盲区位置和大小的数学表达式,从而给出了交替极化阵列对消盲区的数学表征方法。进而分析了交替极化阵列对消盲区的分布规律与影响因素,发现阵元间距能够显著影响交替极化阵列对消盲区的分布,且交替极化阵列对消盲区比共点极化阵列对消盲区大,表明相比于共点极化阵列,交替极化阵列虽然通过减少天线数目降低了设备成本,但增大了阵列的对消盲区。

基于对消盲区模型进行了数值仿真。在M=4、λ=0.1 m、χ1=12.6 dB、SNR=20 dB、INR=40 dB条件下,仿真得到了d∈(0,2λ)时对消盲区占比图与不同阵元间距下对消盲区分布图,结果证明了理论分析的正确性。

最后,利用信道模拟器搭建了实验平台,通过调整信道间相位与功率,模拟了给定空间来向、极化状态的干扰,在与仿真相同的参数下,实验测得的对消盲区与理论值基本一致,再次证明了理论分析的正确性。