基于曲线拟合误差估计的阻抗优化识别方法

彭 阳, 王 跃, 刘永慧, 郜凯杰

(西安交通大学电气工程学院电气绝缘与电力设备国家重点实验室, 陕西 西安 710049)

0 引 言

以风能、太阳能为代表的新能源在电网中的渗透率日益提高,变流器、储能装置等设备也越来越多地应用于电网中[1-6]。这些设备在给电网带来灵活性的同时,也带来了谐振不稳定和影响电能质量等新问题,使雷达系统、舰船系统、数据中心之类大型复杂装备面临更加复杂的用电环境[7-9]。

基于阻抗信息的稳定性分析方法,不需要设备的结构和参数等先验知识,因此被广泛用于供配电系统稳定性和可靠性分析[10-11]。由于其分析结果的精确度强烈依赖于阻抗信息的准确性,因此如何精准识别变流器的输出阻抗成为了近年来研究的热点[7,12-13]。传统的阻抗识别使用等间隔扫频法[14-17],即在宽频带范围内,等频率间隔地连续注入小信号进行测量,并用线性插值的方法拟合出宽频带完整阻抗数据。这种方法虽然简便易用,但在被测量设备结构和参数未知情况下,难以合理地设置测量频率间隔[18]。如果间隔过大,则可能漏掉阻抗共振峰;如果间隔过小,则需要较长的测量时间和较大的测量代价,另外过度测量也会影响系统的工作状况从而影响测量的准确性[19-21]。

针对这些问题,文献[22]提出了一种阻抗测量自适应频率注入方法,该方法通过测量误差估计不断动态选择新的测量点,直到测量误差小于预先设定的阈值为止。这种方法能够在共振峰分布更多的测量点,在阻抗变化平缓处分布更少的测量点,与传统的等间隔扫频方法相比,能够以更少的测量点来获得相同的测量精度,但其性能取决于用户事先设定误差阈值,高度依赖于设计者的经验。文献[18]提出了一种频率响应采样优化方法,该方法是在最大测量估计误差区间中选择测量点,实现频率测量点选择的全局优化,从而达到快速减少总测量误差的目的。在测量频率点数一定的情况下,这种方法比其他方法在易用性、稳定性、准确性和数据继承性等方法有更良好表现。

上述方法的误差估计方法基本相同,都是采用分段线性插值函数来近似真值函数。然而,供配电系统中的阻抗变化是非线性的,变化曲线是平滑的,分段线性插值得到的带有拐点的拼接线段与阻抗曲线的非线性平滑变化曲线特性不同。这种特性上的差异会导致拟合的部分必然存在误差,且误差的大小由测量对象的非线性程度决定[23-24]。

另外一个问题是,分段线性插值方法对已测量点信息的利用率不高。任何一个线性分段只利用了其始点和终点信息,不能利用其他测量点的信息。但对于非线性曲线,其上的任意一小段曲线不仅受其始点和终点的影响,而且还受其左右若干点的影响,相当于利用了更多的测量点的信息,使曲线更接近真值曲线。

针对现有方法存在的问题,本文提出一种新的基于曲线拟合误差估计的阻抗优化识别方法,给出了非线性阻抗曲线拟合方法,以及相应的误差估计方法、测量点优选方法和阻抗识别优化流程,并通过仿真验证了方法的有效性。与现有方法相比,本文方法能够更快地识别阻抗特性曲线上的共振峰,在采样点一定的情况下能够使识别总误差更小,在识别总误差一定的情况下需要的测量代价更小。另外,本文方法的时间复杂度和空间复杂度较小,能够满足阻抗测量的实时性要求,具有良好的工程实用价值。

1 端口阻抗在线测量方法

被测设备在稳态工作点附近的特性可以认为是线性的,因此在线测量设备端口的阻抗,就是测量设备在稳态工作点下的小信号阻抗。

在线测量端口阻抗的过程可以等效成如图1所示的拓扑。其中,被测设备可以看作一个黑箱,需要关注的是其端口的特性,不必关注其内部的复杂控制算法。在测量过程中,首先注入一个频率为fp的电压小信号vp,然后通过响应信号检测部分,测量加入扰动后的电压vp和电流信号ip。检测后的信号经过信号处理后,滤出信号中fp的分量,再通过阻抗计算,即可得到fp频率点下的端口阻抗:

图1 在线测量端口阻抗的等效拓扑Fig.1 Equivalent topology for online measurement of port impedance

(1)

式中:Z为阻抗的复数表示形式;vp(fp)和ip(fp)分别为变流器端口电压和电流在频域下的表示形式。

为了便于进行数值分析,通常将测量的阻抗分解成幅值和相位的形式:

(2)

式中:zm为阻抗的幅值;‖·‖为求幅值运算;zp为阻抗的相位;∠为求相位运算。

2 基于广义加性模型的阻抗曲线拟合方法

广义可加模型是一种适用于非线性对象的曲线拟合模型[25-26],一般形式如下:

y=α+f1(x1)+f2(x2)+…+fp(xp)

(3)

式中:y为模型的输出;α是曲线截距,是一个常数;xi为模型的输入;f1(x1),f2(x2),…,fp(xp)是输入变量到输出变量的特征变换预测函数,是一种非参数平滑函数,用于控制输入变量与输出变量间的非线性效应。

由于广义加性模型对于非线性对象精准的拟合特性,因此,本文将此模型引入到端口阻抗拟合的研究中。

对于一个特定工作点的系统而言,拟合阻抗曲线就是需要找出频率f和阻抗幅值m和相位p之间的关系。针对阻抗曲线的拟合,阻抗幅值zm和阻抗相位zp的广义加性模型分别如下:

zm=αm+fmf(f)

(4)

zp=αp+fpf(f)

(5)

式中:fmf和fpf分别是阻抗幅值和阻抗相位的平滑函数,我们选择回归样条函数作为其基本形式。回归样条函数能将含多个峰顶和峰谷的复杂形状的阻抗曲线,划分为多个分段进行求解。回归样条函数能够将函数的形式表示为多个基函数的组合。

以幅值计算公式为例,平滑函数fmf的回归样条函数可以表示为

(6)

式中:bj为基函数;βj为基函数的系数;q为表达式的阶数。

对于给定的控制节点K=(kj:j=1,2,…,q-2),基函数[27-28]如下:

(7)

式中:R(f,kj)的计算公式为

(8)

基函数系数可以用最小二乘法求解,即求解式(9)的一阶导数为0时系数的值:

‖Ym-Fβ‖2+λβTSβ

(9)

式中:Ym是已测阻抗的幅值的向量表示;F为已测频率的向量表示;β是基函数系数的向量表示;λ是平滑度参数。

式(9)中的‖Ym-Fβ‖2为残差平方和,即测量得到的阻抗幅值与函数fmf计算的阻抗幅值之间差值的平方和。根据最小二乘法,‖Ym-Fβ‖2取最小值时,整体拟合误差最小,即‖Ym-Fβ‖2的一阶导数为0时整体误差最小,据此可以计算出β的值。

式(9)中的λβTSβ为惩罚项,其中λ是人工设定的参数,用于控制曲线的平滑程度,使曲线不致过于弯曲或平直;S按下列公式计算:

(10)

式中:R按照式(8)计算。

综上所述,给出基于广义加性模型的非线性阻抗曲线拟合算法如算法1所示。

算法 1 非线性阻抗曲线拟合算法IF_Curve输入Y为阻抗幅值或相位,F为注入信号的频率,K为控制节点,λ为平滑参数输出α,β为阻抗曲线的截距常量和基函数系数

1:Function IF_Curve2:n=F中的频率点个数 3:q=K中控制节点个数+2# 使用式(7)计算的基函数矩阵4:Basis=1f1R(f1,k1)…R(f1,kq-2)1f2R(f2,k1)…R(f2,kq-2)︙︙︙⋱︙1fnR(fn,k1)…R(fn,kq-2)5:# 使用式(10)计算的惩罚矩阵Penalty=00P(k1,λ)…P(k1,λ)00P(k2,λ)…P(k2,λ)︙︙︙⋱︙00P(kq-2,λ)…P(kq-2,λ)6:# 拼接形成最小二乘矩阵系数XaXa=Basis Penalty7:# 使用最小二乘法求解截距和系数α,β=Lstsq(Xa,Y)8:returnα, β9:End Function

3 阻抗曲线拟合误差估计方法

在选择新的测量点时,需要估计拟合曲线与真值曲线之间的误差。这个误差估计得越准确,新选择的测量点对减少全局误差的贡献就越大,反之可能会选择不合适的测量点,导致宝贵测量点资源的浪费。因此,拟合误差估计的准确性十分重要,直接影响阻抗测量方法的性能。

本文所述的拟合误差是基于拟合的阻抗特性曲线估计的,也就是图2(a)中的黑色虚线和绿色实线所包围的面积。该区域所包围的面积越大,说明两条曲线之间的差别越大,拟合误差也就越大;反之,则说明拟合误差较小,拟合结果较好。由于系统结构未知,真值曲线无法获得,因此无法直接计算非线性拟合曲线和真值曲线之间的误差。为了解决这个问题,我们在相邻测量点连接一条辅助线段,如图2(b)和图2(c)中红色虚线所示。借助这条辅助线段,先估计真值曲线与辅助线段之间的误差,如图2(b)中灰色阴影区域所示,称为误差1,记为errm_1[fi,fi+2];然后再估计非线性拟合曲线与辅助线段之间的误差,如图2(c)中黄色竖杆区域所示,称为误差2,记为errm_2[fi,fi+2]。

图2 非线性拟合曲线的拟合误差估计Fig.2 Fitting error estimation of nonlinear fitting curve

分别估算出误差1和误差2后,即可得到阻抗曲线在局部区间[fi,fi+2]内的非线性拟合误差,计算方法如下:

errm[fi,fi+2]=errm_1[fi,fi+2]-errm_2[fi,fi+2]

(11)

其中,误差1可以通过拉格朗日插值理论进行间接计算,误差2可以通过逐步积分的方法进行计算。下面分别对于误差1、误差2和整体拟合误差的估计方法进行说明,然后给出误差估计算法。

3.1 误差1估计方法

误差1指的是真值曲线与辅助线段所包围的面积,如图3中的灰色阴影所示。

图3 误差1的等效估计方法Fig.3 Equivalent estimation method of Error 1

以阻抗幅值为例,记图3中的真值曲线为Tm(f);红色的虚线辅助线为Lm(f)。则在任意频率f下两者之间的差值为

Em1(f)=Tm(f)-Lm(f)

(12)

因此,对于图3中的区间[fi,fi+1]和[fi+1,fi+2],对应的阴影面积可分别表示为

(13)

(14)

对于区间[fi,fi+2],根据定积分的代数和性质,可将误差1表示为

(15)

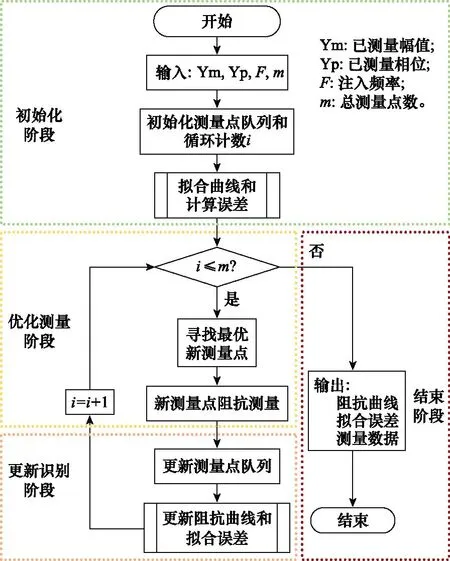
根据一阶牛顿-柯特斯闭型积分公式,在使用直线段逼近曲线积分的过程中,任一区间[fi,fi+1]上一定存在一个点ci,且fi

(16)

式中:hi为区间长度,hi=fi+1-fi。

类似地,对于区间[fi+1,fi+2],也有:

(17)

对于区间[fi,fi+2],也有一个ci, i+2,能够接近由直线段(zmi, zmi+2)逼近曲线的误差:

(18)

式中:S(fi,zmi,fi+2,zmi+2)为直线段(zmi, zmi+2)在区间[fi,fi+2]上的积分结果,即(fi, zmi,fi+2, zmi+2)所包围的梯形面积。

类似的,对于线性函数Lm(f),在区间[fi,fi+1]上的积分实际上就是梯形(fi, zmi,fi+1, zmi+1)的面积,记为S(fi, zmi, fi+1, zmi+1)。

因此,联立式(13)和式(16),可得

(19)

类似地,联立式(14)和式(17),也有

(20)

当区间较小时,可以近似地认为hi=hi+1=h/2,Tm″(ci,i+1)=Tm″(ci+1,i+2)=Tm″(ci,i+2)。根据闭型积分的区间可叠加性,联立式(19)和式(20),可得到误差1的表达式,即

(21)

将式(18)与式(21)相减,可得

(22)

(23)

3.2 误差2估计方法

误差2指的是非线性拟合曲线与辅助线段之间所包围的面积,如图4中的橘色阴影所示。在任意频率f下,两者之间的差值为

图4 误差2的等效估计方法Fig.4 Equivalent estimation method of Error 2

Em2(f)=Tm(f)-Lm(f)

(24)

由于非线性拟合曲线和辅助线段都是根据已知的测量数据进行拟合得到的,因此误差2可以直接通过积分表示:

(25)

对于式(25),可以利用梯形法则近似求解,如图4右边等效小梯形分解所示。假定将区间[fi,fi+2]划分为p等分,每一等分的长度为δh,那么误差2也可以表示成

(26)

式中:

(27)

3.3 整体拟合误差估计方法

在整个阻抗识别过程中,另一个需要计算的是完整宽频带阻抗曲线的整体拟合误差。

已知当前有n个测量点的数据,那么将第1,2,…,n-2测量点开始的各区间非线性拟合误差,分别记为errm[f1, f3],errm[f2, f4],…,errm[f(n-2), fn]。由于所计算的区间为每3个测量点所组成的两段误差之和,每一个区间所计算出来的误差与前一区间的误差有重叠部分,因此计算整体拟合误差时需要每次跳过一个区间的误差进行累加,以避免误差被重复计算。

当测量点数n为奇数时,宽频范围内阻抗曲线被分成了偶数个局部区间,此时曲线整体拟合误差为

(28)

当测量点数n为偶数时,宽频范围内阻抗曲线被分成了奇数个区间。如果仍然采用式(28)计算整体拟合误差,那么最后局部区间的第二个频段的误差未被计算在内。这种情况下,整体拟合误差应该是所有偶数局部区间的误差,加上最后一个频率区间的误差,而频率区间的误差可以近似最后一个局部区间误差的二分之一。这样,当测量点数n为偶数时,整体拟合误差的计算公式为

(29)

综合前面的讨论,设计阻抗曲线非线性拟合误差估计算法2所示。

算法 2 阻抗曲线非线性拟合误差估计算法IF_Erro输入Y为阻抗幅值或相位,F为注入信号的频率,Z为阻抗幅值或相位的拟合曲线输出errm, errmall:局部区间拟合误差和整体拟合误差1:Function IF_Error2: n=注入信号的频率点个数3: errm_1=根据式(23)估计的误差14: errm_2=根据式(26)估计的误差25: # 计算各局部区间的拟合误差 errm=abs(errm_1-errm_2) 6: Ifn为奇数 then7: errmall=根据式(28)估计的 n为奇数时的整体拟合误差

4 阻抗优化识别方法

根据前面介绍的阻抗非线性曲线拟合方法和误差估算方法,提出基于非线性拟合的阻抗识别优化方法。本方法的基本思想是:首先利用已测量点拟合出阻抗特征曲线,接下来估计每个局部区间的拟合误差,然后在误差最大的区间新增测量点。重复上述步骤直到满足测量结束控制条件为止。测量结束控制条件可以是测量总点数,也可以是整体拟合误差。本文仅讨论测量总点数为控制条件的情况。

阻抗优化测量与识别过程分为初始化、优化测量、更新识别和结束4个阶段,如图5所示。

图5 阻抗优化测量与识别过程Fig.5 Impedance optimization measurement and identification process

步骤 1初始化阶段

这一阶段的主要工作是为后续阶段准备数据、拟合曲线和估计误差。

如果前期未进行任何测量,则需要在宽频带范围内均匀测量4个频率点下的阻抗数据,作为启动阻抗测量优化流程的初始条件。如果前期已进行过测量,则利用已测量的数据作为启动阻抗测量优化流程的初始条件。除此之外,还需要指定总测量点数作为结束测量过程的条件。

在初始阶段的最后,根据已测量的阻抗数据,利用前面介绍的算法IF_Curve拟合阻抗曲线,利用算法IF_Error估计局部区间的拟合误差和整体拟合误差,作为下一步测量优化的依据。

步骤 2优化测量阶段

这一阶段的主要工作是根据局部区间拟合误差,选择全局最优的新测量点并进行测量。

首先找出误差最大的局部区间,选择这样区间有利于使整体拟合误差以最快的速度减少,并有利于快速找到阻抗显著变化的点。

接下来在误差最大的局部区间内,确定一个频率点作为新测量的频率。按照全局优化的测量思想,新测量点应该在拟合误差最大的局部区间中选定,这样能使测量总误差以最快的速度减少,并有助于尽快找到阻抗急剧变化的频率点。

为了保证测量稳定性,需要注意以下细节。

(1)曲线的选择。由于幅值曲线和相位曲线形状不同,两个曲线的最大拟合误差局部区间也不一定相同。为了取得较好的性能,应该在具有最大拟合误差的曲线上选择局部区间。

(2)最大拟合误差局部区间的选择。具有最大拟合误差的局部区间可能不止一个,这时可以选择频率较小的复合区间,因为较小频率区间中的阻抗变化可能更剧烈。

(3)频率段的选择。局部区间包含有两个频率段,其拟合误差是两个频率段的误差之和,并且无法将估计误差分解到每个频率段,因此存在在哪一个频率段新增测量频点的问题。第1种方案是在频率宽度较大的频率分段中确定新测量点,如图6(a)中绿色五角星所示。第2种方案是在两个频率分段各增加一个新测量点,如图6(b)中两个绿色五角星所示。

图6 新频率点的选择方案Fig.6 Selection scheme of new frequency points

从节省测量资源的角度来考虑,本文使用第一种方案。需要注意的问题是,当两个频率段的频率宽度一致时,应该选择频率较小的频率分段。确定新增测量点的频率段后,我们选择该频率段的中点的频率作为新增频率点的频率。

步骤 3阻抗更新阶段

这一阶段的主要工作是将上一阶段测量得到的阻抗数据加入到已测量数据集合中,并利用算法IF_Curve和IF_Error重新拟合曲线并估计误差。

步骤 4结束控制阶段

这一阶段的主要工作是判断阻抗测量过程是否结束。如果满足阻抗测量结束条件,则结束测量过程,并输出测量数据、阻抗曲线和拟合误差。如果未达到阻抗测量结束条件,则重复步骤2和步骤3。需要说明的是,阻抗测量结束条件既可以是测量的总点数,也可以是整体拟合误差的大小。在这里为了方便分析拟合效率,采用测量的总点数为循环终止的控制条件。

5 算例验证

本节通过仿真算例来验证所提方法的有效性。对比的对象为线性拟合的采样优化方法[18],这是目前文献中效率较高的一种方法。

在阻抗识别过程中,系统阻抗测量的环节采用仿真来实现,阻抗测量频率范围为10～5 000 Hz,仿真所用到的算法部分采用Python 3.9版实现。在输出结果的对比工作中,采用单频率注入法的结果作为真值阻抗曲线的数据,测量频率范围为10～5 000 Hz,测量间隔为0.5 Hz,真值数据共99 800个点。

5.1 直接电流控制型系统的阻抗识别

首先,我们采用了一个阻抗特性和控制策略都较为简单的直接电流控制型系统[29-31],对其进行阻抗识别,拟合结果如图7所示。

图7 电流控制型系统阻抗识别结果Fig.7 Impedance identification results of the current controlled-based system

图7(a)和图7(b)为拟合结果的一个局部片段(10～100 Hz),从两种方法的结果中可以看出,在50 Hz的阻抗尖峰处,本文所提的方法能够准确的找到尖峰,并能够在附近进行较为精准的拟合;而传统线性拟合识别方法对于幅值和相位的尖峰都无法精准地找到。这说明,在同样的测量次数下,本文的方法相较于传统的方法而言,能够更快地捕捉到所有显著变化点,精准地抓取阻抗特性。另外,从图7(c)的误差趋势图中也能看出,在迭代初始、测量点极少时,两种方法的误差之间差距不大;但随着迭代次数的增加,本文所提的方法能够更加快速地降低误差,并且在整个过程中均能保持误差相对较小。这说明,本文的方法在实现过程中也具有很好的稳定性。

5.2 基于虚拟同步机算法系统的阻抗识别

这个算例中,采取了一种控制环节较多、端口阻抗特性较为复杂的控制算法,即虚拟同步机算法来控制系统[32-34],并对其进行阻抗识别,拟合结果如图8所示。从图8(a)中可以看出,此时本文所提方法已经能够精准地捕捉出阻抗曲线和相位曲线中存在的3个尖峰,在尖峰处进行了在线测量;并且在尖峰附近的拟合趋势也非常接近真值曲线。而对于传统的线性采样优化方法来说,图8(b)中显示,此时在线测量的频率点均位于高频的线性区间,并不能够为阻抗特性的抓取带来高效的信息;低频位置处的拟合效果也很不理想,拟合结果并不能完全反映此时系统阻抗的趋势和特性。另外,从图8(c)的误差趋势图中也能看出,随着迭代次数的增加,本文所提的方法能够更加快速地降低误差,并且在整个过程中均能保持误差显著地小。这说明,本文的方法在实现过程中也具有很好的稳定性。

图8 虚拟同步机算法系统阻抗识别结果Fig.8 Impedance identification results of the virtual synchronous generator-based system

6 结束语

针对无法获取设备的结构和参数等先验知识的阻抗识别场景,建立了阻抗特性广义加性模型,研究提出了阻抗特性曲线非线性拟合方法,以及相应的误差估计、测量点优选方法,实现了基于非线性拟合的阻抗测量优化和特性识别,为研判供配电系统的可靠性和稳定性提供依据。与现有基于分段线性插值的方法相比,一方面本方法能够使测量总误差减少得更快,所需测量点数量更少,获得的测量精度也更高。其次,本方法能够更快地测量到阻抗曲线上的突变尖峰,能够为分析系统的震荡频率提供关键信息;另外能够更快地测量到阻抗曲线的显著变化点,从而能够以较少的测量代价更快地形成阻抗曲线基本形状。

随着新能源在电力系统中渗透率的日益提高以及电力电子设备的广泛使用,大型信息化装备面临日趋复杂的供配电环境,如何利用人工智能和大数据技术来更快速准确地获取阻抗信息,并进行供配电可靠性分析,是未来需要进一步深入研究的重要课题。