面向通信系统的误码率计算方法
2022-03-31张卓伟
张卓伟,朱 润,沈 凡
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
通信在现代战争中发挥着不可替代的作用[1],通过对接收到的通信信号进行解调解码分析可以为战场上的战斗指挥部署提供情报支撑[2-3]。误码率作为通信的一项重要技术参数,是衡量通信系统数据传输可靠性的先决条件[4-6],因此在通信系统下研究误码率计算方法对通信系统寻求更优化的解调解码方法具有重要的理论指导意义。
刘家昊等[1]对通信干扰方程进行了修正,通过误码率求得信噪比门限,进一步得到等效干信比,对系统的通信抗干扰能力进行了预测;王浩[4]以误码率为依据,分别建立了基于时间序列法和回归分析法的可靠性预测模型,取得良好的预测效果;高建贞等[5]分析了高斯白噪声环境下超宽带脉冲的误码性能,仿真结果表明脉冲幅度调制的误码性能要优于脉冲位置调制;王文娟等[6]对高斯最小频域键控调制方式下的误码率性能进行了仿真分析,仿真结果表明误码率随着信噪比的增加而减小。已有研究大都通过误码率来评价系统的可靠性,但没有给出通信情形下的误码率计算方法。
本文提出了一种针对通信系统在视距传播距离内的误码率计算方法:给出视距传播距离计算模型,利用提出的输出信号解调信噪比计算模型计算出信噪比,通过误码率与信噪比的相对关系求出误码率,最后仿真验证了本文方法的有效性。
1 误码率计算方法设计
1.1 视距传播距离计算模型
在标准大气折射情况下[1]无线电通信视距传播距离计算公式为
(1)
式中,ht、hr分别为发射天线和接收天线架高,m;d为视距传播距离,km。
1.2 视距通信条件下输出信号解调信噪比计算方法
(1) 视距通信条件下传输损耗计算模型
在视距传播距离内,信号的传输损耗可通过自由空间损耗模型计算,自由空间损耗模型如下:
Ls=32.4+20lgf+20lgD
(2)
式中,f为频率,MHz;D为距离,km。
此外,在计算信号传输损耗时还需要考虑天线对不准、大气吸收及雨雾雪天气等引起的额外损耗L1,故通信时信号传输的总损耗可通过下式计算:
L=32.4+20lgf+20lgD+L1
(3)
(2) 输出信号解调信噪比计算模型
设接收机的信道带宽为Be,系统的噪声系数为NF,接收灵敏度为Si,要求的输出信号的解调信噪比为k,则接收灵敏度由下式计算:
Si=-114+NF+10lgBe+k
(4)
若信号的发射功率为Pt,发射天线增益为Gt,接收天线增益为Gr,为使接收机处的电平满足要求,则须满足下式:
Pt+Gt+Gr-L≥Si
(5)
整理得
Pt+Gt+Gr-L+114-NF-10lgBe≥k
(6)
1.3 误码率计算方法
误码率是指在信号传输过程中码字产生错误的概率[4]。在给定调制方式的条件下,通过误码率与比特信噪比的关系式即可获得与比特信噪比相对应的误码率。不同调制方式下比特信噪比与误码率的关系式如表1所示,其中Eb为单个比特的信号能量,N0为噪声功率谱密度,Eb/N0为比特信噪比,erfc(x)为互补误差函数,Q(x)为高斯Q函数[1]。

表1 不同调制方式下比特信噪比与误码率关系
erfc(x)和Q(x)分别定义为
(7)
(8)
信噪比与比特信噪比的相对关系如下:
(9)
式中,SNR为信噪比;η=Rb/W为频谱效率。
将式(9)转换为对数形式,整理得
(10)
式中,k为SNR的对数形式,dB。
所以在给定k和η的条件下即可得到与k相对应的比特信噪比,从而得到与k相对应的误码率。
2 仿真与分析
2.1 视距传播距离的计算
此处ht取9 000 m,hr取25 m,则计算得到视距传播距离d为411.46 km。
2.2 视距通信条件下输出信号解调信噪比分析计算
为使D在视距传播距离内,本文中D取340 km,L1取3 dB,Pt取1 010 W,Gt取0.1 dB,Gr取0 dB,Be取3.1 MHz,NF取5.5 dB,f分别取961 MHz、1 001 MHz、1 101 MHz、1 214 MHz。MSK、FSK、QPSK调制方式下的η分别取1 bit/s/Hz、1 bit/s/Hz、2 bit/s/Hz,则在视距传播距离范围内不同频率下的输出信号解调信噪比如表2所示。

表2 不同频率下的输出信号解调信噪比
可以看出,传输损耗随着频率的增加而增加,信噪比随着频率的增加而降低。
2.3 误码率分析计算
为确定与计算出的输出信号解调信噪比相对应的误码率,需要对误码率与比特信噪比关系进行仿真。本文通过调用MATLAB中的“Bit Error Rate Analysis Tool”工具箱对MSK、FSK、QPSK调制方式下的误码率与比特信噪比关系进行仿真。仿真时设置比特信噪比的起始值和终止值分别为0 dB、30 dB,步进为0.000 1 dB,仿真得到的误码率分析如图1所示。
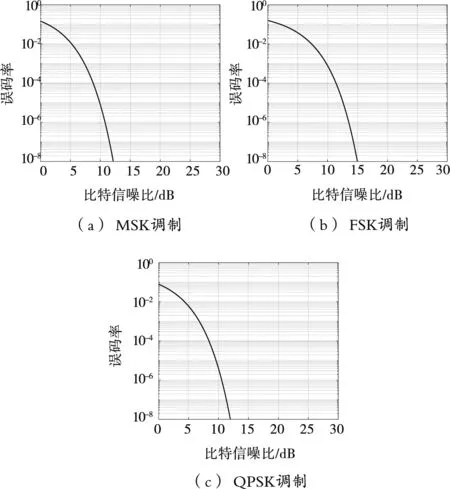
图1 不同调制方式下的误码率分析图
在得到不同调制方式下的误码率分析图后,通过MATLAB读入图片中的数据,即可查询得到与输出信号的解调信噪比对应的误码率。不同频率/调制方式下的误码率如表3所示。
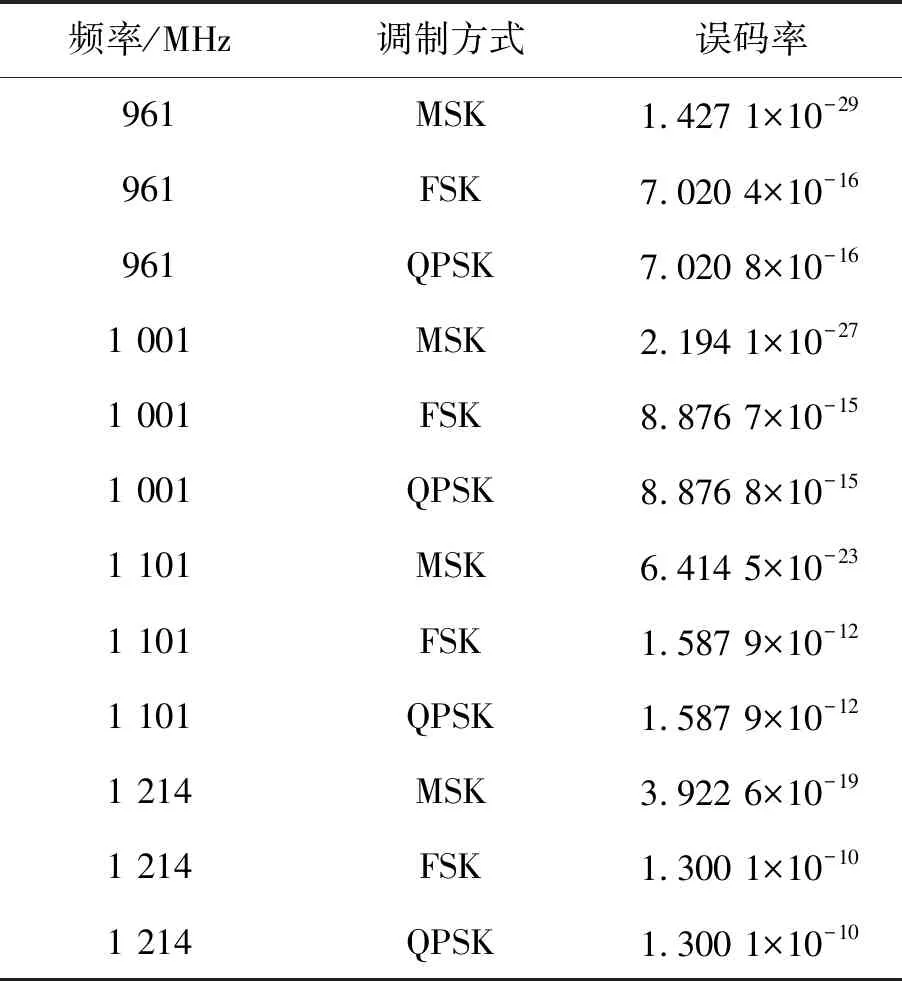
表3 不同频率/调制方式下的误码率
可以看出:当频率相同时,通信系统采用MSK调制方式的信号传输误码率要低于采用FSK、QPSK调制方式的误码率;当调制方式相同时,通信系统的误码率会随着频率的提高而增大;在961~1 214 MHz频带范围内,系统采用MSK、FSK、QPSK调制方式的误码率都低于10-5,数据传输的可靠性较高。本文方法能有效用于视距传播距离条件下的误码率计算。
3 结束语
本文提出了一种在视距传播距离条件下的通信系统误码率计算方法。在视距传播距离内,通过提出的输出信号的解调信噪比计算模型求出信噪比,再利用信噪比与误码率间的关系得到误码率,并通过仿真验证本文方法的有效性。仿真结果表明:在视距传播距离内,当频率一定时,系统采用MSK调制方式时的误码率性能要优于FSK调制和QPSK调制。此外,当调制方式一定时,系统的误码率会随着频率的提高而提高。
