未知姿态目标航磁异常探测的最优飞行方向分析

石 昱, 卞雷祥,*, 庄志洪, 付梦印, 王春娥, 秦 杰

(1. 南京理工大学机械工程学院, 江苏 南京 210094; 2. 南京理工大学电子工程与光电技术学院,江苏 南京 210094; 3. 南京理工大学自动化学院, 江苏 南京 210094;4. 北京自动化控制设备研究所, 北京 100074)

0 引 言

随着安静型潜艇技术的发展,大多数潜艇航行噪声已接近甚至低于海洋背景噪声[1],声探测等传统探测方法面临极大难度。磁异常探测(magneic anomaly detection, MAD)被认为是有效的非声探潜手段之一[2]。此外,MAD在资源勘探[3-5]、未爆弹探测[6-8]、与地震预测[9-10]等领域也发挥着重要作用。

目前,MAD算法的定位精度与探测概率都依赖于信号的信噪比,基于磁张量缩并量正交基分解的目标探测定位算法,在信噪比低于-20 dB条件下,检测效果受噪声影响较大,无法确定检测能量的峰值点[11];在噪声均方根为0.01 nT的条件下,总场梯度(total field gradient, TFG)-张量缩并量梯度(tensor contraction gradient, TCG)定位方法中三轴的最大定位误差接近0.8 m[12]。Wang等人[13]利用迭代算法对传统三角定位测量(scalar triangulation and ranging, STAR)方法中的非球面误差进行了补偿,该方法在信噪比为40 dB、20 dB时,定位误差分别在1%、8%左右,而传统STAR方法此时的定位误差分别在15%、20%附近。Yin等人[14]对基于归一化磁源强度(normalized source strength, NSS)的STAR方法进行了仿真分析,仿真中该方法的探测范围约为15 m,当信噪比高于19.4 dB时,相对位置误差小于5%;当信噪比为-3 dB时,基于噪声检测的随机共振法探测概率降到了70%[15];信噪比为-3 dB时,高阶过零法(high order zero crossing, HOC)探测概率为0.74～0.82[16]。

对于隐匿目标的磁异常探测,需要选择合适的探测路径方向来获得高信噪比的磁异常信号,提升目标的探测识别概率与定位精度。曲晓慧等人[17]利用蒙特卡罗法仿真了几个特定飞行航向下磁探仪的搜潜概率,仿真结果表明飞机沿南北方向飞行搜索概率更大。吴芳等人[18]仿真了多个飞行航向下的目标磁异常信号,结果表明反潜机探测航向为0°(南北方向)、45°时,磁异常信号变化幅度皆大于其他探测航向。 Moser[19]研究了12个飞行航向下的目标磁异常信号,不同航向下磁异常信号峰峰值差异明显,其中30°方向时信号变化幅度最大,但南北方向信号变化幅度与其极为接近。Schluckebier[20]分析了磁异常探测中飞机飞行航向与水下目标航向对探测距离的影响,无论水下目标的航向如何,飞行航向为南北方向时,磁异常探测距离都较大。

上述的研究[17-20]通过对多个特定探测路径方向的磁异常信号进行比较,说明了沿着南北方向的磁感应强度变化较大。实际上,铁磁性目标磁矩与其结构、姿态有关,运动目标的姿态是变化的,建立探测路径上磁异常信号与目标姿态的定量关系,对于规划路径和目标特性反演定位均具有重要意义。

本文针对典型目标建立了磁矩精确计算模型,利用该模型建立了目标磁异常信号与其姿态之间的定量关系;计算并分析了航磁探测时飞行平面内磁异常变化最大路径与背景磁场(地磁场)之间的关系,以此得到磁异常探测的最优飞行方向,最后借助多物理场仿真软件进行了验证。

1 理论分析

1.1 铁磁性目标磁矩计算模型

1.1.1 实心铁磁性目标的磁矩

在分析目标磁性时,只考虑固定磁性与感应磁性。固定磁性在短期内不会发生变化,感应磁性会受到磁性目标的姿态、形状、体积、材料特性以及地磁场等因素的影响。因此,需要根据上述因素建立磁矩计算模型。

铁磁性目标的磁矩M可以表示为

M=VJtotal

(1)

式中:Jtotal为目标的总磁化强度,由感应磁化强度与剩余磁化强度两部分组成;V为磁性目标的体积。

铁磁性目标的载体坐标系如图1所示,l为其长轴方向;t为其短轴方向;v为其竖直方向。

图1 铁磁性目标的载体坐标系Fig.1 Carrier coordinate system for ferromagnetic targets

铁磁性目标在l,t,v方向上的磁矩Ml,Mt,Mv可以表示[21-25]为

(2)

式中:Nl,Nt,Nv分别为铁磁性目标在l,t,v方向上的退磁系数;HEl,HEt,HEv为地磁场在l,t,v方向上的分量;Jtl,Jtt,Jtv为总磁化强度在l,t,v方向上的分量;Jrl,Jrt,Jrv为剩余磁化强度在l,t,v方向上的分量;χ为材料的磁化率;χ=μr-1,μr为相对磁导率。

不规则形状铁磁体的退磁因子难以通过理论计算得到精确值。本文利用有限元软件仿真计算出典型目标在地磁场中产生的磁矩值,将结果代入式(2),得到l,t,v3个方向上的退磁因子Nl,Nt,Nv,可以表示为

(3)

1.1.2 空心铁磁性目标的磁矩

水下目标一般为空心铁磁体,空心铁磁体与实心铁磁体产生的磁场成一定比值,可以根据实心铁磁体的磁矩来计算空心铁磁体的磁矩。假设空心球体内外径之比为k,空心球体H空与实心球体H实之间产生的磁场比值R可以表示[26-27]为

(4)

当μr较大,k接近于1(球壳很薄)时R可以表示[21]为

(5)

空心铁磁性目标各方向上的内外径之比不统一,其在l,t,v方向上的磁场比值Rl,Rt,Rv可以表示为

(6)

式中:kl、kt、kv分别为铁磁体在l,t,v方向上的内外径之比。

可以借助多物理场仿真软件计算出实心与空心铁磁体在l,t,v方向上的磁矩之比,将结果作为Rl,Rt,Rv。

那么,空心铁磁性目标在其载体坐标系上产生的磁矩Mls,Mts,Mvs可以表示为

(7)

1.1.3 铁磁性目标在不同姿态下的磁矩

目标的姿态信息以及地磁场方向与探测坐标系的关系如图2所示。假设探测坐标系x轴正方向为地理北,y轴正方向为地理西,z轴竖直向上。HE为地磁场,HExy为地磁场在xy平面(水平面)上的投影;I为HE与HExy之间的夹角,称为磁倾角,I下倾时磁倾角为正,上仰时为负;D为HExy与地理北方向之间的夹角,称为磁偏角,磁偏角东偏时为正,西偏时为负;l为目标的长轴方向,lxy为长轴在xy平面上的投影,α为lxy与地理北之间的夹角,称为方位角,左偏为正;β为l与lxy之间的夹角,称为俯仰角,下倾为正。

图2 地磁场与目标姿态示意图Fig.2 Schematic diagram of geomagnetic field and target attitude

目标姿态变化相当于载体坐标系在探测坐标系下发生旋转。目标方位角与俯仰角分别为α、β时,载体坐标系相对于探测坐标系的运动如下:

(1) 绕z轴旋转角为α;

(2) 绕y轴旋转角为β。

绕z轴旋转的变换矩阵Rot(z,α)可以表示为

绕y轴旋转的变换矩阵Rot(y,β)可以表示为

对应的变换矩阵R(α,β)可以表示为

(8)

与R(α,β)对应的逆变换矩阵R(-β,-α)可以表示为

(9)

地磁场在目标载体坐标系(l,t,v)上的分量HEl,HEt,HEv可以表示为

(10)

式中:HE为地磁场值。

那么,剩磁在目标载体坐标系(l,t,v)上的分量Jl,Jt,Jv可以表示为

(11)

通过联立式(2)、式(7)～式(11)可以得到目标在探测坐标系下的磁矩。

铁磁性目标在探测坐标系与载体坐标系上的磁矩之间的关系可表示为

(12)

式中:MT=[Mx,My,Mz]T,MT为实心铁磁性目标在探测坐标系上的磁矩;MC=[Ml,Mt,Mv]T,MC为实心铁磁性目标在载体坐标系上的磁矩;MTS=[Mxs,Mys,Mzs]T,MTS为空心铁磁性目标在探测坐标系上的磁矩;MCS=[Mls,Mts,Mvs]T,MCS为空心铁磁性目标在载体坐标系上的磁矩。

1.2 铁磁体磁场的分布规律

利用磁偶极子模型可以计算出铁磁性目标在空间中的磁场分布情况,空间中某测点(x,y,z)的磁场B可以表示[28]为

(13)

式中:μ0=4π×10-7;r为目标与测点之间的相对位置矢量;M为目标的磁矩,可表示为

其中,[χHEl+Jrl,χHEt+Jrt,χHEv+Jrv]T可以表示为

(14)

该点产生的标量磁异常信号S可以表示[3]为

S=B·ie

(15)

式中:ie为地磁场方向的单位向量。

实际探测过程中载体平台工作时所处的平面如图3所示。假设载体平台在z=600 m的xy平面内飞行,利用式(13)～式(15)可以计算出在探测平面内磁场分布情况,从而找到磁异常信号变化最大的路径及其方向。假设探测平面内磁场强度的最大值、最小值位置分别为A(xmax,ymax),B(xmin,ymin),探测平面内磁异常信号变化最大的路径方向为AB(xmax-xmin,ymax-ymin)。在进行磁异常探测时,测线一般只能布置在载体平台所处的飞行平面内,由式(13)～式(15)可知飞行平面内磁场变化最大路径主要与目标磁矩和地磁场有关,为此需要通过计算地磁场与磁矩在飞行平面内的投影以及平面内磁异常信号变化最大路径之间的夹角来分析三者之间的关系。

图3 飞行探测示意图Fig.3 Flight detection diagram

飞行平面内磁异常信号变化最大的路径所在直线与磁矩投影的夹角σxy可以表示为

(16)

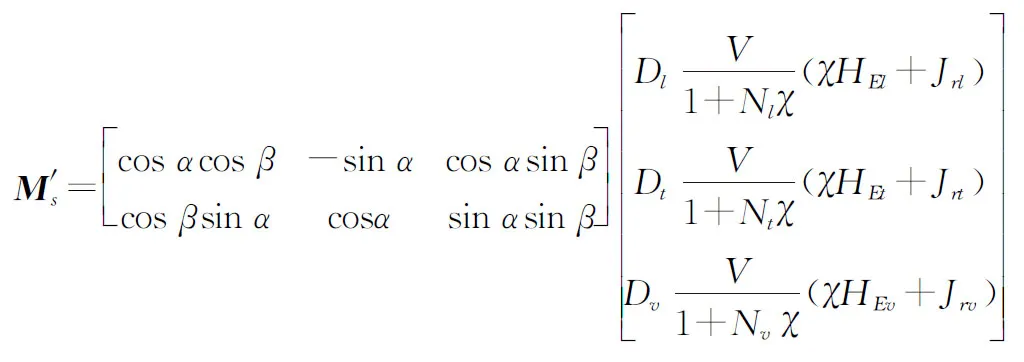
其中,[χHEl+Jrl,χHEt+Jrt,χHEv+Jrv]T可以表示为

(17)

飞行平面内磁异常信号变化最大的路径所在直线与地磁场投影的夹角γxy可以表示为

(18)

(19)

2 数值计算与仿真分析

2.1 水下目标磁矩的数值计算与仿真

假设水下目标为如图4所示的圆柱形薄壳铁磁体,将目标几何参数设置为:半径4.5 m,总长度84 m,两端半球体半径4.5 m,薄壳的厚度0.2 m;目标磁导率设置为200,剩余磁通密度设置为50 A/m[29];参考文献[30]对地磁场参数进行设置:地磁场强度BE=50 000 nT,I=44°41′,D=-3°07′,假定地磁场值恒定;方位角α设置为0°～360°,俯仰角β设置为-90～90°,角度变化为1°。

图4 水下目标模型Fig.4 Underwater target model

根据磁矩计算模型,得到水下目标磁矩随其姿态的变化特性如图5所示。目标磁矩的模值随目标姿态变化范围为3.55×105～2.42×106A·m2,最小值是最大值的14.67%,当目标长轴与地磁场方向一致时取最大值,当目标长轴与地磁场方向垂直时取最小值,目标长轴方向与地磁场方向偏离越大,目标的磁矩值越小。

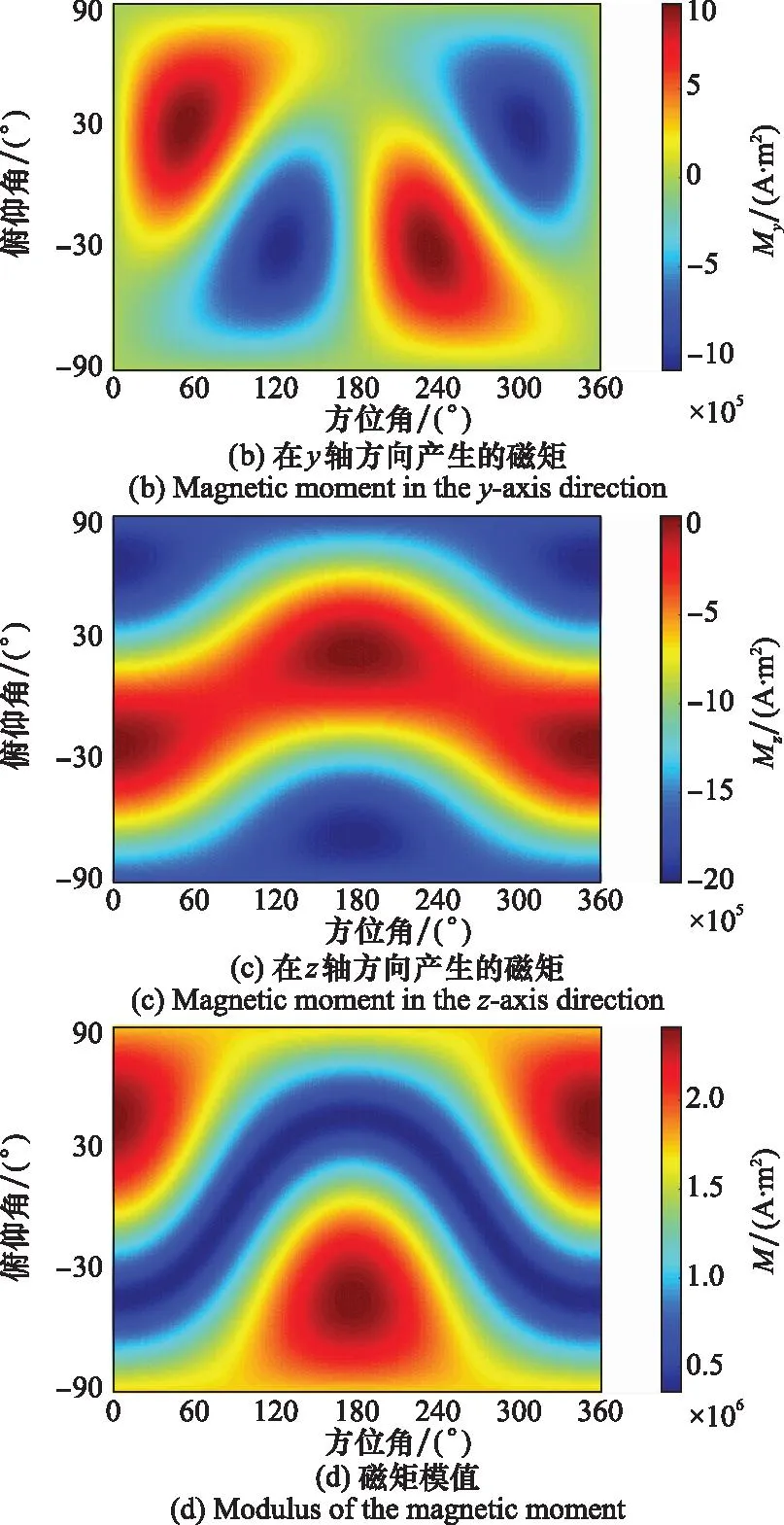
图5 水下目标磁矩在不同姿态下的数值计算结果Fig.5 Calculation results of magnetic moments of underwater targets in different attitudes

使用多物理场仿真软件对水下目标磁矩随其姿态的变化特性进行仿真,由于有限元仿真计算量过大,将角度变化设置为30°,其余参数与数值计算中的设置保持一致。仿真结果如图6所示,磁矩模值变化范围为3.57×105～2.34×106A·m2,目标在不同姿态的磁矩仿真结果与对应的磁矩模型计算结果差异为0.003%～0.04%,造成差异的原因可能是仿真软件中网格划分的不够细致。

图6 水下目标磁矩在不同姿态下的仿真结果Fig.6 Simulation results of magnetic moments of underwater targets in different attitudes

2.2 磁异常探测最优飞行方向分析

将z=600 m处的xy平面设置为载体平台所处的飞行平面,其余参数设置与第2.1节中保持一致。利用磁矩计算模型与式(13)～式(19)可以计算出飞行平面内磁异常信号变化最大的路径所在直线与磁矩投影的夹角σxy、以及与地磁场投影的夹角γxy随目标姿态的变化特性,进而分析出飞行平面内磁矩投影方向、地磁场投影方向与磁场变化最大路径之间的关系,得到磁异常探测最优飞行方向。

σxy随目标姿态的变化特性如图7所示。当目标处于不同姿态时,σxy的变化范围为0°～89.996 4°。当目标处于某些姿态时,例如方位角为135°,俯仰角为70°时,σxy为87.66°,已接近两个不同直线之间夹角所能达到的最大值(90°)。此时,沿着磁矩投影方向进行磁异常探测显然是不合理的。当俯仰角为-30°～30°时,σxy最大值为44.158 8°,且35°以上区域面积很小,此时沿着磁矩方向探测可获得变化幅度较大的磁异常信号曲线,但在实际磁异常探测中目标的磁矩信息是无法预知的。

图7 σxy随目标姿态的变化特性Fig.7 Variation characteristics of σxy with target attitudes

当目标处于不同姿态时,γxy随目标姿态的变化特性如图8所示。当目标处于不同姿态时,γxy的变化范围为0°～50.045 7°,且变化范围主要为0°～40°,仅当方位角在90°/270°(目标长轴垂直于地磁场方向)左右,俯仰角在±30°左右时,γxy的变化范围为40°～50.045 7°。地磁场在平面内的投影方向与磁异常变化最大路径方向基本一致。

图8 γxy随目标姿态的变化特性Fig.8 Variation characteristics of γxy with target attitudes

如图7和图8所示,在目标姿态、磁矩信息未知的条件下,飞行平面内地磁场投影与磁异常变化最大路径方向偏差较小。此外,地磁场在平面内的投影方向可事先通过测量地磁场获取,因此沿着地磁场在平面内投影方向的探测路径是较优的选择。

目标上方飞行平面内沿地磁场投影的磁异常信号变化量对于飞行平面内最大变化量的占比REM可以表示为

(20)

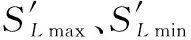
利用磁矩计算模型与式(13)～式(15)可以计算出目标正上方600 m处载体飞行平面内各点的磁感应强度大小。将计算结果代入式(20)可得REM随目标姿态的变化特性如图9所示,当目标处于任意姿态时,REM的变化范围为78%～100%;当γxy减小时,沿地磁场投影方向与探测平面内磁异常变化最大的方向偏离程度降低,这两个方向的磁异常变化幅度相差就越小,由式(20)可得REM增大,反之亦然,这使得图8与图9相似。对比图8可知,当γxy处于最大值附近区域时REM取到最小值,当γxy处于最小值区域时REM取到最大值;γxy越大REM越小,γxy越小REM越大,γxy小于35°时,REM基本都在90%以上。无论目标处于何种姿态,在目标正上方沿地磁场飞行获取的磁异常变化量总是飞行平面最大变化量的78%以上。因此,在目标姿态和磁矩信息未知的情况下,沿地磁场在飞行平面内的投影方向飞行是最优的选择。

图9 REM随目标姿态的变化特性Fig.9 Variation characteristics of REM with target attitudes

利用多物理场仿真软件获取不同方向测线的磁异常信号,对上一段的结果进行验证,为减小计算量,只针对目标特定的姿态进行仿真,将目标姿态角设置为:α=80°、β=26°,此时σxy为14.29°、γxy为50.1°。其他参数设置与第2.1节中保持一致。将测线设置在水下目标正上方600 m处,只改变测线与地磁场投影的夹角来获得磁异常信号曲线。沿着磁矩在平面内投影、地磁场在平面内投影设置两条测线;其他测线分别与沿着地磁场投影方向测线的夹角为30°、60°、90°、120°、150°。仿真结果如图10所示,图中磁异常信号变化最大的测线是与地磁场投影夹角为30°的测线,该条测线与磁异常变化最大路径方向的夹角最小;沿着地磁场投影测线的磁异常信号变化幅度为该平面内最大变化的88.50%,理论计算结果为84%,差异可能是仿真软件在计算磁场分布时,空间中点与点之间的间隔设置过大使某些点的磁场数据丢失所引起的。

图10 磁异常信号仿真结果Fig.10 Simulation of magnetic anomaly signal

3 结 论

为了优化航磁探测中的飞行探测路径以达到提高磁异常信号强度的目的,本文综合考虑目标的固定磁性与感应磁性,根据其结构、姿态等参数以及地磁场值建立了目标磁矩的计算模型,利用该模型可精确地计算出典型目标在地磁场中产生的磁矩;利用目标磁矩的计算模型与磁异常计算公式建立了探测路径上磁异常信号与目标姿态的定量关系。推导公式数值计算结果与商用多物理场仿真软件仿真结果吻合,结果表明:当目标处于任意姿态时,其正上分沿着地磁场在平面内投影的磁异常信号变化量约为平面内最大变化量的78%～100%,这也就意味着在目标姿态和磁矩信息未知的情况下,沿地磁场在飞行平面内的投影方向飞行是最优的选择。后续将进一步开展缩比目标探测的验证实验。