基于非脉冲矢量网络分析仪的非反向交叉眼干扰实验设计与分析

2024-01-16刘永才杨浩楠

系统工程与电子技术 2024年1期

周亮, 孟进, 刘永才, 李伟, 杨浩楠

(海军工程大学舰军用电力科学与技术研究所船综合电力国防科技重点实验室, 湖北武汉 430033)

0 引言

单脉冲雷达通过瞬时多波束技术测量目标的角度,具有测角精度高、抗干扰能力强的特点,被广泛用于导弹末端精确制导系统,实现对舰船等动目标实施精确打击。为了提高导弹的突防能力,导弹末端雷达制导可分为主动单脉冲雷达、干涉仪(被动单脉冲雷达)和复合制导。

交叉眼干扰技术是对抗单脉冲雷达最有效的方式之一[1-3]。对此,大量学者对交叉眼干扰技术展开了研究,可分为非反向交叉眼干扰和反向交叉眼干扰两类。对于非反向交叉眼干扰技术研究,文献[4-5]基于角闪烁理论建立了交叉眼干扰模型;文献[6-7]以被动雷达或干涉仪为对象,分析了交叉眼干扰对被动雷达的作用效果;文献[8]考虑雷达脉冲相干积累对交叉眼干扰性能的影响;文献[9]分析了非反向交叉眼干扰信号传输路径对交叉眼干扰性能的影响。对于反向交叉眼干扰技术研究,文献[10-13]对考虑目标回波和幅相波动分布模型的两源反向交叉眼仿真模型、幅向误差容限和干信比展开了建模和分析;文献[14]分析了两源反向交叉眼对主被动复合单脉冲雷达的干扰效果;由于两源反向交叉眼增益随干扰机幅相参数变化敏感,文献[15-20]对考虑目标回波和隔离目标回波的多源线阵反向交叉眼干扰机的幅相容限和干信比展开了分析;文献[21]对隔离平台目标回波条件下的两源反向交叉眼干扰和多源线阵反向交叉眼干扰的幅相容限展开了对比分析。针对两源和多源线阵反向交叉眼干扰角度覆盖扇面有限的问题,文献[22-23]研究了两组两源反向交叉眼干扰的组阵方式,并分析了两组两源反向交叉眼干扰信号传输路径差对交叉眼干扰效果的影响;文献[24-27]分别建立了多源圆形阵、正交旋转阵和任意四元阵的反向交叉眼干扰模型,分析了不同干扰机转角下交叉眼增益的稳健性。

以上研究均未涉及交叉眼干扰实验设计,对非反向交叉眼干扰研究主要考虑干扰信号传输路径的影响。文献[28-29]分析了天线极化失配对交叉眼干信比和效果的影响。文献[30]在微波暗室环境下,基于脉冲矢量网络分析仪、环形器、幅相调节器件和微带天线设计了反向交叉眼干扰实验,对基于扩展性分析方法的反向交叉眼干扰模型展开了验证,由于环形器的隔离度有限,其要求矢量网络分析仪具备可控的脉冲收发功能和信号数据采集功能,以通过加时间窗的方法滤除环形器耦合的自激信号。以上试验研究主要设计了基于环形器和脉冲矢网的反向交叉眼干扰实验系统,要求矢量网络分析仪具备发射脉冲信号和信号数据采集等功能,且未涉及非反向交叉眼干扰试验方法。

针对交叉眼干扰多侧重于仿真建模、实验设计及实施复杂等特点,本文基于交叉眼干扰技术原理和单脉冲测角原理,结合矢量网络分析仪幅相精确测量的特性,设计了基于非脉冲矢量网络分析仪、移相器、衰减器和天线的非反向交叉眼干扰实验系统。首先,在微波暗室环境下开展了基于矢量网络分析仪的无源方位测角实验;然后,开展了交叉眼干扰原理验证实验;最后,通过电磁仿真软件对干扰天线相位中心展开了仿真建模,分析了干扰天线的非互易性对实验效果的影响。论文研究可为交叉眼技术测试、工程实现提供一定的参考。

1 交叉眼干扰建模

1.1 交叉眼干扰场景描述

交叉眼干扰机与单脉冲雷达位置关系如图1所示。反向交叉眼干扰机信号转发过程如图2所示。当单脉冲雷达发射的电磁信号抵达干扰机接收天线1、天线2后,将天线1接收的信号调制后由天线2发出,天线2接收的信号调制后由天线1发出。单脉冲雷达接收到信号后,通过比较接收信号相位差对雷达指向进行调整,直至单脉冲雷达差通信信号相等时锁定搜索目标。图1中黑色实心方框表示单脉冲雷达指向的视在假目标,θr为雷达视轴相对干扰机中心的转角,θe为干扰天线相对于雷达视轴的半张角,θc为干扰天线相对与雷达的转角,θi为雷达视轴相对假目标的转角,θ1和θ2为干扰机天线1、天线2与单脉冲雷达中心法线方向的夹角,dc为干扰机天线间的距离,R0为单脉冲雷达中心到交叉干扰中心的距离。

图1 雷达与干扰机相对位置Fig.1 Relative position of radar and jammer

图2 交叉眼干扰机的反向天线结构Fig.2 Reverse antenna structure of cross-eye jammer

与反向交叉眼干扰机不同的是,非反向交叉眼在信号收发过程[9-10]中,其信号传播路径不存在互易性,雷达发射的信号仅由天线1或天线2接收,调制后由天线1和天线2同时发出。

1.2 交叉眼干扰建模

文献[10-13]在建立两源反向交叉眼干扰模型时,其应用场景均为雷达与交叉眼干扰机距离较远,在得到交叉眼干扰下雷达指示角与交叉眼幅相参数关系模型时,进行了必要的近似简化,如sin(k1)→k1。受限于微波暗室大小,在实验过程中,交叉眼干扰机天线与雷达天线距离较近,近似简化的前提条件不充足,易形成较大的误差。对此,本文按照非简化模型对反向交叉眼干扰模型和非反向交叉眼干扰模型进行推导,得到近距离交叉眼干扰下的雷达指示角计算方式。

1.2.1 反向交叉眼干扰建模

假设干扰机两路信号幅值强度为(1,α),干扰机两路信号相位差为φ,则干扰机两路信号达到单脉冲雷达天线阵面的强度比依旧为(1,α),相位差依旧为φ,依据反向交叉眼信号空中转发路径,其和通道接收到的信号[11]为

(1)

式中:s为雷达发射信号;ε(s)为单脉冲雷达天线接收到的干扰机发射信号;FΣ(θ1)、FΣ(θ2)分别为单脉冲雷达天线的在θ1、θ2处的和增益。

单脉冲雷达差通道接收到的信号为

(2)

式中:FΔ(θ1)、FΔ(θ2)为单脉冲雷达天线在θ1、θ2处的差增益。

依据单脉冲雷达测角原理,单脉冲雷达指示角为雷达接收差信号与和信号比值的虚部,可得雷达单脉冲比为

(3)

当干扰机天线中心连线与单脉冲雷达天线中心连线近似平行时,θ1、θ2与θr、θe之间的关系为

(4)

(5)

式中:β为玻尔兹曼常数,β=2π/λ;dp为单脉冲雷达两天线相位中心间距;Pr(θ)为单个波束的方向图。联合式(4)和式(5),对式(3)中和部分进行化简,得到:

(6)

令

(7)

采用三角函数中和差化积公式2sinxcosy=sin(x+y)+sin(x-y),对式(6)化简,结合式(7),可得

(8)

而雷达单脉冲斜率与雷达单脉冲指示角关系式[1]为

(9)

联合式(8)和式(9),可得到雷达单脉冲指示角与幅值比和相位差的关系式为

(10)

式中:R[·]为取实数部分运算。

联合式(1)至式(10),可以计算得到交叉眼干扰下的雷达指示角。

(11)

1.2.2 非反向交叉眼干扰建模

与反向交叉眼干扰信号收发路径相比,非反向交叉眼干扰的干扰信号抵达单脉冲雷达天线前,会额外引入了路径差异对两路幅值比和相位差的变化。非反向交叉眼干扰信号达到单脉天线的传播路径如图3所示。其中,d0为假目标到干扰机天线中心的距离,dr为测向天线间的距离。

图3 非反向交叉眼干扰信号空中传播路径Fig.3 Air propagation path of non-reverse cross-eye interference signal

在频率一定情况下,假设射频信号空中传播路长l径引起的幅值和相位变化分别记为a(l)和φ(l),因此非反向交叉眼干扰信号抵达单脉冲雷达天线1和天线2的信号可表示如下所示:

R1(s)=ε(s)·[Pj(θ31)Pr(θ13)a(l1)·ejφ(l1)+
α·ejφ·Pj(θ41)Pr(θ14)·a(l4)·ejφ(l4)]

(12)

式中:Pj为干扰机单个干扰天线方向增益;θij天线i与天线j的连线与水平线的夹角。

R2(s)=ε(s)·[Pj(θ32)Pr(θ23)a(l3)·ejφ(l3)+
α·ejφ·Pj(θ42)Pr(θ24)·a(l4)·ejφ(l4)]

(13)

因此,雷达单脉冲斜率为

(14)

若干扰机与雷达的距离较远时,l1～l4近似相等,其引起的幅度相对变化差异可以近似相等;对于相同的干扰天线和单脉冲雷达接收天线,有

(15)

此时,式(14)可化简为

(16)

联合式(9)和式(14),可以计算近距离非反向交叉眼干扰下的雷达指示角,联合式(9)和式(16),可以计算远距离下非反向交叉眼干扰下的雷达指示角。其中l1～l4的值与dc、R0、θc、dp等相关,在微波暗室实验中,可通过直接测量得到。

2 实验方案设计

根据交叉眼干扰作用机理以及单脉冲测角原理,基于矢量网络分析仪幅相精确测量的特点,本文首先设计了基于矢量网络分析仪的方位维测角系统,利用矢量网络分析仪中的两个端口、1个幅相调整网络和2个条形微带天线模拟无源单脉冲测角雷达或被动单脉冲雷达,矢网剩下的2个端口选取1个端口中作为辐射源;然后在矢网无源精确测角的基础上,设计非反向交叉眼干扰实验系统,从而排除测角系统引起的实验误差。

2.1 无源单脉冲测角实验方案设计

基于矢量网络分析仪的测角系统由四通道的安捷伦N5230A型矢量网络分析仪、1个幅相调整网络、同轴射频线缆、1个喇叭天线和2个条形微带天线组成,如图4所示,其中S1、S2、S3、S4为矢量网络分析仪的4个射频端口。幅相调整网络由两个衰减器、一个移相器组成,用于调节雷达两接收通道幅相,以保证矢量分析仪两接收通道幅相一致性。然后将矢量网络分析仪测量得到的接收通道的幅值比和相位差,代入式(9),在某软件上计算得到雷达的角度值。

图4 基于矢量网络分析仪的无源测角实验系统设计Fig.4 Design of passive angle measurement experiment system based on vector network analyzer

由于干扰天线与单脉冲测角天线间的距离比较近,辐射源天线移动会引起较大的角度变化,以及后期测角过程中,应满足如下条件:

(1) 测角天线的E面波束宽度较宽,保证辐射源天线移动过程中始终位于测角天线主波束宽度内;

(2) 两个测角天线的间距小于λ/2[1],避免出现栅瓣影响天线的测角范围。

2.2 非反向交叉眼干扰实验方案设计

在测角系统的基础上,将单个辐射源替换成2个幅相可控的相参辐射源,从而模拟交叉眼发射两路相位差接近180°、幅值比接近1的两路信号,其由幅相调整网络、功分器和低噪放组成,下文简称交叉眼干扰原理实验样机,实验系统组成如图5所示。

通过调节幅相调整网络中衰减器和移相器的刻度值,使交叉眼干扰机处于不同的幅值比和相位差,进而观察和计算在不同干扰机状态下的雷达指示角。在测角系统条件的基础上,非反向交叉眼干扰实验系统应满足如下条件:

(1) 交叉眼干扰天线和测角天线均在彼此的主波束宽度内;

(2) 交叉眼干扰天线正对单脉冲雷达天线。根据反向交叉眼干扰与非反向交叉眼干扰空间信号传播路径差异,使交叉眼干扰天线正对单脉冲雷达天线,避免信号空间传输路径差异对非反向交叉眼干扰效果的影响。

3 实施过程及结果分析

3.1 实验场景

为减少信号空间多径对实验结果的影响,实验在微波暗室环境下进行,并保证干扰天线和测向天线处于彼此的远场。实验过程中,器件互连采用高频稳相线缆,在幅向调整网络中,幅度采用高精度步进调节器,相位采用1°调节大小的数字移相器。同时采用高增益、窄波束喇叭天线作为干扰发射天线,以减少信号空间多径对测角的影响。实验系统部分参数如表1所示。交叉眼干扰实验场景如图6所示。

表1 实验系统参数Table 1 Radar and jammer parameters

图6 基于矢量网络分析仪的交叉眼干扰试验场景Fig.6 Cross-eye interference test scenario based on vector network

3.2 单脉冲测角实验步骤及结果

3.2.1 单脉冲测角实验步骤

基于矢量网络分析仪的无源单脉冲测角实验步骤如下。

步骤 1通过激光笔对准,使辐射源喇叭天线的馈源位于雷达两天线的中心,此时辐射源相对雷达的实际角度为0°。

步骤 2对矢量网络分析仪S2、S3端口初始化校准,将S2、S3端口经幅相调整网络后与雷达接收天线1和接收天线2相连接,S1端口连接辐射源天线3。

步骤 3调整数控移相器和衰减器的刻度值,观察矢量网络分析仪S21、S31的幅度和相位变化,使S21、S31间的幅度和相位尽量一致。

步骤 4移动辐射源,每移动5 cm分别记录一次矢量网络分析仪S21、S31的幅度和相位值。

步骤 5测量雷达两天线中心与辐射源原点的距离,并在仿真软件中将不同位置记录的S21、S31的幅度和相位代入公式进行计算。

3.2.2 无源单脉冲测角实验结果

辐射源天线位于不同位置时,对上述数据通过软件处理后,得到测量角度与实际角度对比曲线如图7所示。

图7 实际角度与测量角度对比曲线Fig.7 Comparison curve between actual angle and measured angle

分析图7可知,测角角度与实际角度较为一致,误差大小在2°内。

3.3 交叉眼干扰实验步骤及结果分析

在矢量网络分析仪精确测角的基础上,开展交叉眼干扰试验和数据分析。

3.3.1 交叉眼干扰实验步骤

步骤 1用低噪放、功分器和幅相调整网络及天线组成的交叉眼干扰实验样机替换单个辐射源,并将矢网端口1与低噪放相连,将连接两喇叭天线端的射频线分别连接矢量网络分析仪端口2和端口3,调节移相器和衰减器的刻度,记录不同移相器刻度和衰减器刻度下S23的幅值和相位。

步骤 2使交叉眼干扰原理实验样机的干扰天线与固定横架垂直,尽可能保证干扰天线朝向一致,同时使干扰天线中心正对雷达天线中心。

步骤 3将矢量网络分析仪端口2和端口3分别连回雷达天线1和天线2,交叉眼干扰实验样机幅相调整网络端口连回喇叭天线3和4,并测量和记录喇叭天线3和4单个辐射信号时矢量网络分析仪S21和S31的幅值和相位。

步骤 4使喇叭天线3和4同时辐射信号,先调节交叉眼干扰实验样机的移相器刻度,然后依次调节两个衰减器刻度,使两路信号相位差在180°左右变化时,幅值比近似不变,并记录不同移相器、不同衰减器刻度时S21和S31的幅值和相位。

步骤 5在软件中将记录的S21和S31的幅度和相位代入公式进行计算。

3.3.2 实验结果分析

交叉眼干扰原理实验样机喇叭天线1和天线2分时工作时,基于矢量网络分析仪测量得到的S21和S31的幅值比和相位差,以及离线计算的辐射源角度和实际角度如表2所示。

表2 测量的S21/S31数值Table 2 Measured S21/S31 value

从表2可知,雷达测得的辐射源喇叭天线3和天线4的角度大小基本相同,并与实际角度误差约1°,因此喇叭天线3和天线4基本正对单脉冲雷达接收天线中心。

由于幅值比接近0 dB,相位差接近180°时,交叉眼干扰信号功率处于抵消状态,矢量网络分析仪接收的能量过小,测量误差变大,本次测试分别选取交叉眼干扰原理实验机幅值比2 dB和4 dB附近时,不同相位差对应S21和S31的参数。

当使交叉眼干扰实验样机的幅值比维持在2 dB,相位差从50°至250°内变化时,矢量网络分析仪两接收通道的幅值比和相位差变化如图8(a)和8(b)所示,得到的交叉眼干扰下的理论值与实际测量计算值结果如图8(c)所示。

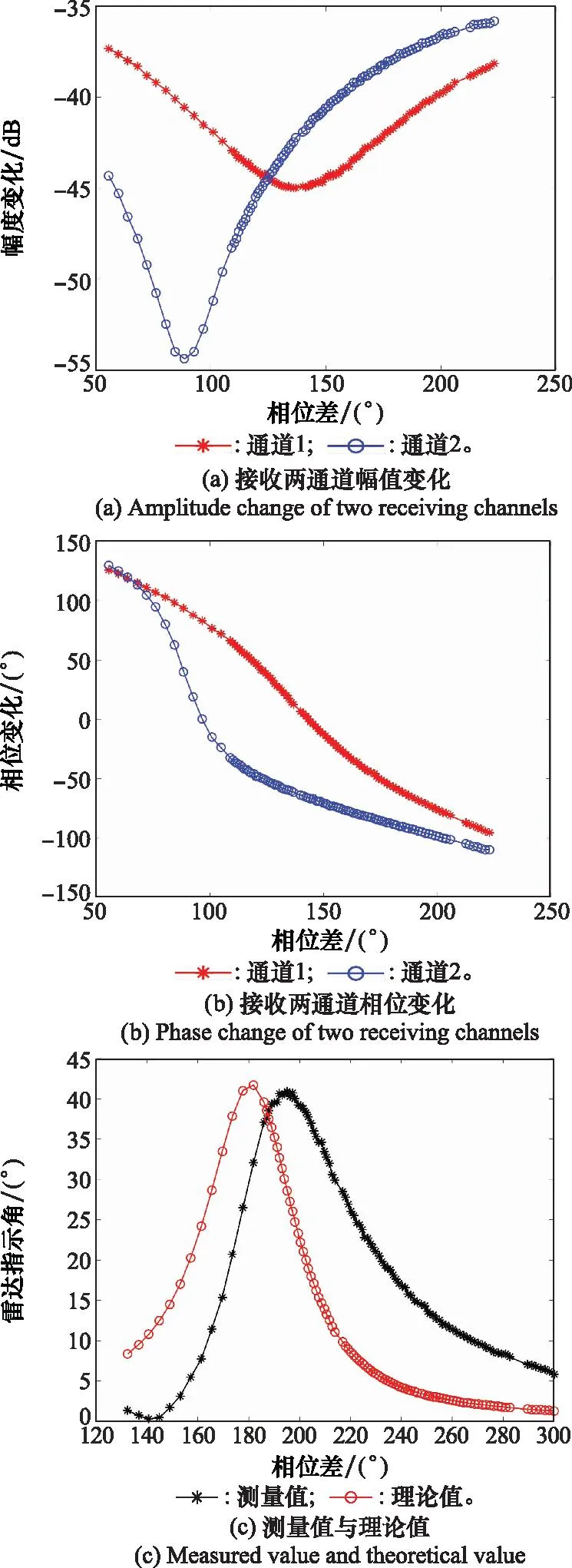
图8 设定幅值比为2 dB附近时对应的角度Fig.8 Corresponding angle when the amplitude ratio is set around 2 dB

当使交叉眼干扰原理实验机的幅值比维持在4 dB,相位差从120°至300°内变化时,矢量网络分析仪接收两通道的幅值比和相位差变化如图9(a)和9(b)所示,得到的交叉眼干扰下的理论值与实际测量计算值结果如图9(c)所示。分析图8和图9可知,测试的角度值与理论角度值变化趋势一致,当幅值比分别为2 dB和4 dB时,测量值在190°处附近的角度值最大,与理论最大值对应的相位差均接近10°。当幅值比为2 dB时,测量的最大角度值与理论最大角度值差约2°;当幅值比为4 dB时, 测量的最大角度值与理论最大角度值的相差约1°,两者的误差变小,这是因为干扰信号抵达测向天线合成后的功率更大,矢量网络分析仪信号处理的信噪比越大。由于干扰天线的半张角约8.23°,无论是幅值比为2 dB或是4 dB,根据式(10)和式(11)换算成交叉眼增益后,其理论值与测量值误差均小于0.5。

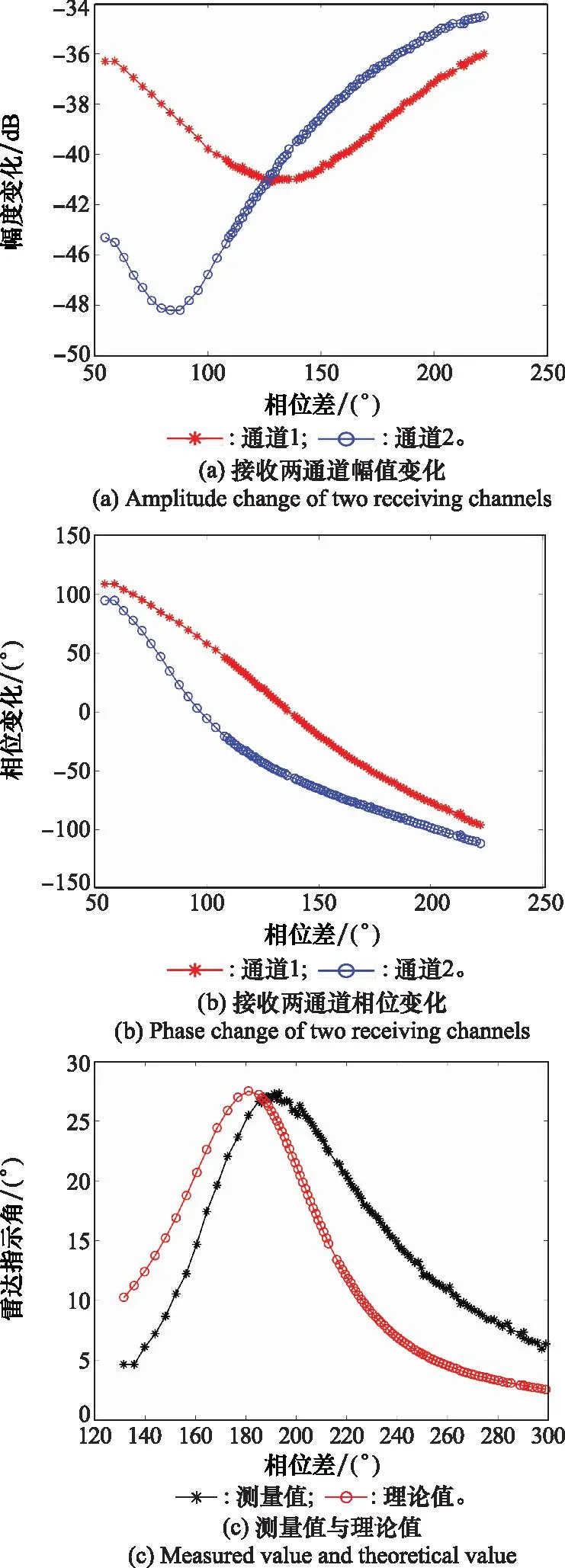
图9 设定幅值比为4 dB附近时对应的角度Fig.9 Corresponding angle when the amplitude ratio is set around 4 dB

3.3.3 误差原因分析

由于干扰机天线采用非反向布局模式,交叉眼干扰实验样机喇叭天线会引入额外的相位误差,而在利用矢量网络分析仪测量交叉眼干扰原理实验机数控衰减器和移相器不同刻度的相位值时,无法将喇叭天线引起相位误差考虑在内。交叉眼干扰实验样机两喇叭天线相位不一致性主要由以下两方面造成,一是天线加工存在公差,微小的公差在微波段会引起相对较大的相位偏差;二是即使两干扰喇叭天线馈源中心与雷达天线中心重合,几何距离上两干扰喇叭天线馈源至测向天线中心相等,理论上可消除非反向交叉眼干扰信号传输路径差异的影响。但喇叭天线的相位中心靠近喇叭口面中心,当两喇叭天线相对于测向天线的朝向不一致时,两者的相位中心点不同,在空中路径上会引起新的相位差。对此,本文利用HFSS软件对交叉眼干扰原理实验机的喇叭天线的相位中心展开仿真,仿真模型如图10所示,分别仿真喇叭天线不同转角对应的喇叭天线相位中心,发现不同转角时相位中心会发生变化,如两个喇叭天线转角相差10°时,相位中心在H面差约5 mm,E面相差约4 mm。

图10 喇叭天线仿真模型(E面)Fig.10 Horn antenna simulation model (Side E)

但通过对比分析图8(c)和图9(c)可知,在干扰机天线与雷达天线相对位置不变时,干扰天线相位中心引入的路径差异比较固定,论文开展的实验中其相对值为10°,可通过交叉眼原理实验样机的幅相网络对相位进行调整,对其进行补偿,进而实施反向交叉眼干扰实验。

4 实验系统对比分析

通过第3.3节理论结果与试验结果的对比分析可知,本文设计的交叉眼干扰试验系统可行。通过第1.2节反向交叉眼干扰与非反向交叉眼干扰模型可知,当交叉眼干扰天线正对单脉冲雷达天线时,非反向交叉眼干扰信号传播路径相等,非反向交叉眼干扰演变成反向交叉眼干扰。因此,通过将交叉眼干扰天线正对单脉冲雷达天线,可部分开展反向交叉眼干扰验证试验。文献[25]基于环形器和脉冲矢网设计的反向交叉眼干扰实验系统,由于交叉眼干扰机为转发体质,要求基于矢网模拟的单脉冲雷达主动发送信号,干扰机才能对模拟的雷达信号进行转发,进而对雷达形成干扰,因此其模拟适用场景只能针对主动单脉冲雷达。在模拟交叉眼干扰类型和单脉冲雷达类型、交叉眼干扰机和矢量网络分析仪对信号处理功能要求以及模拟交叉眼与单脉冲雷达对抗所适应得场景等方面,本文设计的交叉眼干扰试验系统与文献[25]设计的交叉眼干扰试验系统对比如表3所示。