基于操作力矩的三偏心蝶阀动作特性研究

龙威，郁学军，董成，周星宇，3，俞经虎，3

(1.江南大学机械工程学院，江苏无锡 214013；2.无锡斯考尔自动控制设备有限公司，江苏无锡 214013；3.江苏省食品先进制造装备技术重点实验室，江苏无锡 214013)

0 前言

随着工业技术的不断发展，蝶阀因结构简单且低压工况下密封性良好应用越来越广泛，尤其是在石油化工、天然气和其他流体管道输送系统中。三偏心蝶阀在执行开关动作时，流经阀体的流体产生的动水力矩、三偏心蝶阀蝶板自身重心力矩、轴承扭矩等都会随着蝶阀开度变化而改变[1]，使蝶阀动作到一定开度时出现驱动力矩不足的情况，导致阀轴运动不平稳、卡涩等故障。

蝶阀动水力和动水力矩有多种版本计算式，各版本之间结果差异较大[2]。肖而宽等[3]分析了不同版本的计算式之间出现数百倍差值的原因，建立了量纲一致的修正计算式，提出由静水力直接推算最大动水力和最大动水力矩的简化计算方法。刘华坪等[4]对4种常见阀门流动进行了动态数值模拟，得到了开关过程中的流动状态与阀体受力情况，结果表明阀门的开启过程与关闭过程并非简单的反过程。韩志杰等[5]提出对三偏心蝶阀进行内部流场数值模拟，通过改变阀门的3个偏心值研究偏心与流通性能间的关系。季雷雷、何世权[6]根据现有研究得到的动水力矩曲线，利用CFD、Fluent等软件对桁架过流式三偏心蝶阀的动水力矩进行了模拟计算，并通过优化有效地降低了动水力矩。以上研究充分表明有限元仿真的方法用于阀门流场研究的可行性。

本文作者通过有限元软件Fluent对三偏心蝶阀内部流场进行仿真分析，计算动水力矩，并通过动水力矩公式推算蝶阀动水力矩系数，通过AMESim模拟单作用气动执行器活塞的运动，以此来研究三偏心蝶阀阀轴的运动状态。

1 操作力矩原理与仿真建模

1.1 有限元仿真模型

三偏心蝶阀相对于普通中线蝶阀增加了3个偏心值。图1所示为三偏心蝶阀偏心原理，其中α为轴向偏心，表示轴中心线偏离阀体和阀板的几何中心，此偏心使得密封能够完全紧密环绕接触整个阀座；b是密封面偏离轴中心线的距离；角度θ表示密封面的锥面轴线偏离于阀板几何中心，可在关闭和开启过程中减小摩擦作用。三偏心蝶阀在机械磨损、密封性能、使用寿命、耐热耐腐蚀等方面都有明显的优势[7-8]。

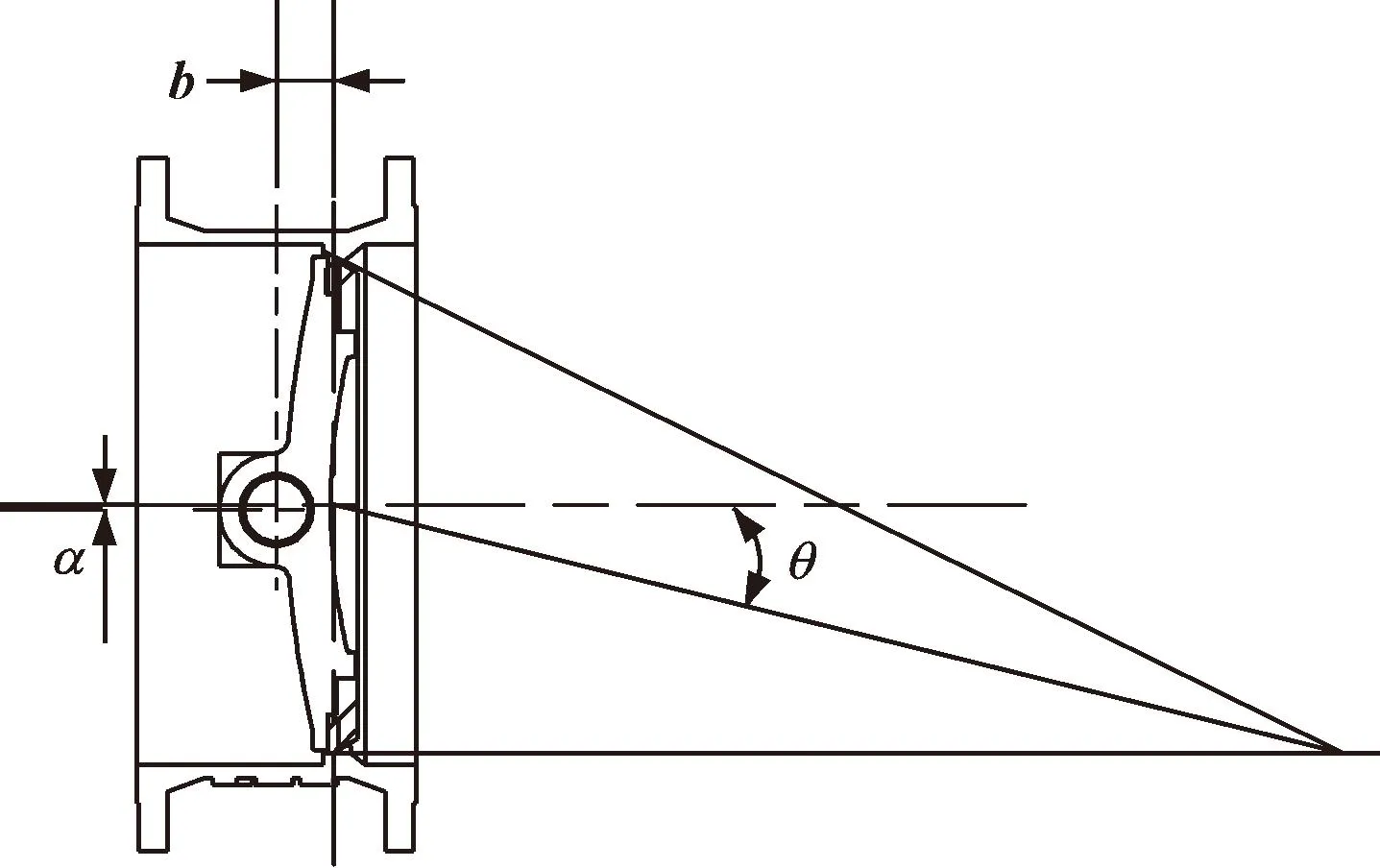
图1 偏心原理Fig.1 Eccentric principle

文中以DN400、PN10(口径为400 mm，公称压力为1 MPa)的三偏心蝶阀为研究对象，其偏心值为α=4 mm，b=44 mm，θ=14°。为了得到内部流场的真实流动情况，保证仿真结果的准确性，在三维建模软件中直接对蝶阀实际模型以布尔求差的方式抽取流道，并依据GB/T 30832推荐，流体入口延长段取5倍蝶板直径，出口延长段为10倍。

1.2 三偏心蝶阀操作力矩原理

蝶阀操作扭矩由蝶板位置及阀门安装类型等几个要素组成，这些要素对阀门操作扭矩影响的计算式如下。

开阀扭矩：

Tt=Tb+Tcg+Td+Tp

(1)

式中：Tb为轴承扭矩；Tcg为重心扭矩；Td为动水力矩；Tp为填料与轮毂摩擦力矩。

轴承扭矩Tb是阀轴与轴承之间摩擦产生阻力矩，计算公式为

(2)

式中：Dd为蝶板直径；d为阀轴直径；Cf为轴和轴套之间静态摩擦因数；Δp为蝶板上压降。

重心扭矩Tcg是蝶板重心偏移导致的，当阀轴位于水平面安装时，出现此扭矩，计算公式为

Tcg=WCgcosθ

(3)

式中：W为蝶板重力；Cg为重心到蝶板关闭状态时距离；θ为实际通过阀板重心的垂直线与轴心线之间角度。

动水力矩Td是蝶阀设计中一个重要参数，与打开蝶阀所需要的扭矩值有着重要关联[9]，量纲一化后的蝶阀动水力矩表达式[10]为

(4)

式中：Ct为以动压为基准的阀门动水力矩系数；ρ为流体密度；v为流体流速；D为管道直径。

填料与阀轴摩擦力矩Tp是蝶阀填料与阀轴之间摩擦产生的力矩，计算公式[11-12]为

Tp=0.6πpd2fh

(5)

式中：p为管道中流体介质压力；f为填料摩擦因数；d为阀轴直径；h为填料高度。

1.3 网格划分及边界条件

为了更容易地控制网格大小和节点密度，采用非结构化网格划分，对蝶板附近及细小特征处的网格进行加密处理，四面体网格总数量在250万～300万之间，蝶阀网格划分如图2所示。在三偏心蝶阀最大许用压差条件下设置边界条件，压力入口分别为0.05、0.1、0.3 MPa，压力出口为0 MPa，参考压力为一个标准大气压，流体介质为水(密度为998.2 kg/m3，黏度为0.001 003 kg/(m·s))，湍流模型为标准κ-ε模型，求解方式用二阶迎风格式SIMPLE，从入口开始进行初始化，收敛条件为残差小于10-3。

图2 三维流域网格Fig.2 3D watershed grid

1.4 单作用气动执行器建模

危险工况下，带有弹簧复位的单作用执行器的最大优势在于断电后可以通过弹簧复位关闭阀门，降低危险系数，因此通常作为三偏心蝶阀的驱动机构。其常用拨叉机构传动如图3所示，力臂L始终保持不变，可以将随开度变化的操作力矩转化成施加在活塞右侧的力。

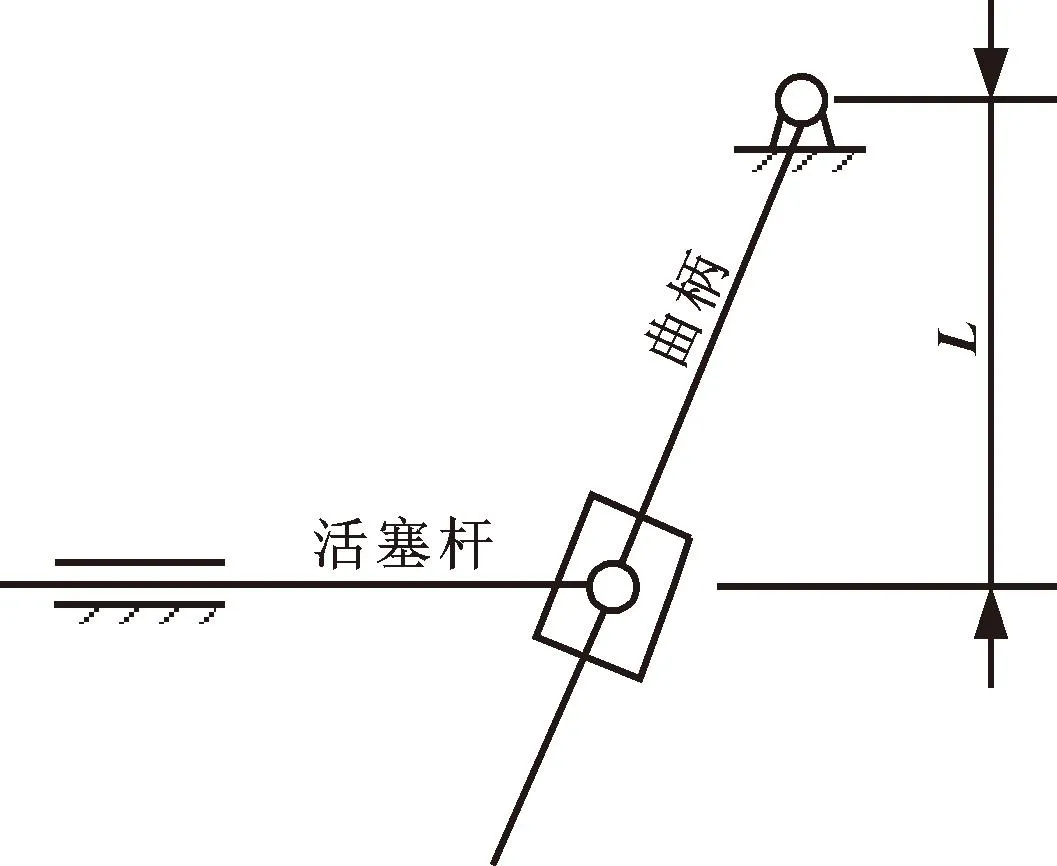
图3 单作用执行器传动机构Fig.3 Single acting actuator drive mechanism

文中重点研究动水力矩对开阀动作影响，通过AMESim软件对单作用执行器进行建模仿真，建模主要用到机械模块库、HCD(液压元件)库和PCD(气压元件)库[13]，模型如图4所示。

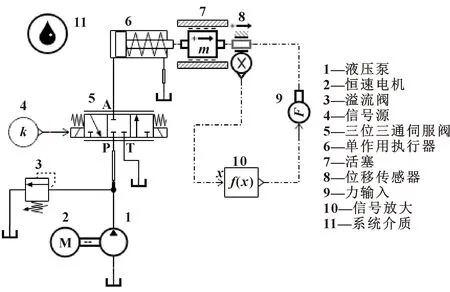
图4 单作用气动执行器Fig.4 Single acting actuator

气动系统介质为空气，通过溢流阀3控制进入气缸的压力不超过0.45 MPa，信号源4控制三位三通阀右位工作，单作用执行器6活塞直径为350 mm，活塞杆直径为40 mm，活塞初始速度为0，长度为330 mm，弹簧刚度为8 000 N/m，活塞7质量为33.7 kg，并通过位移传感器8将位移转化成信号，最后通过元件9和10将信号再转化成随位移变化的力。

2 结果与分析

2.1 流场仿真结果分析

对三偏心蝶阀流场进行三维定常数值仿真计算，设定不同阀板开度，得到蝶阀在10°、20°、30°、40°、50°、60°、65°、70°、80°、90°开度下管道内部流场情况、蝶板动水力矩及其系数的变化规律。当入口压力为0.1 MPa时，在10°、40°、65°、90° 4个典型开度下蝶阀对称面速度云图如图5所示。可以看出：入口段的流速小于出口段流速，随着蝶板开度的增大，平均流速及最大流速都在增加，但流动状态更平稳，流速分布更加均匀。同时在65°开度之前，流道内存在漩涡，对动水力矩平稳性有较大影响；在65°开度之后，漩涡明显减少甚至消失，对平稳性的影响减小。当蝶板开度较小时，蝶板密封面处的速度较大，密封面冲刷严重；随着蝶板开度增加，密封面的冲刷减弱。

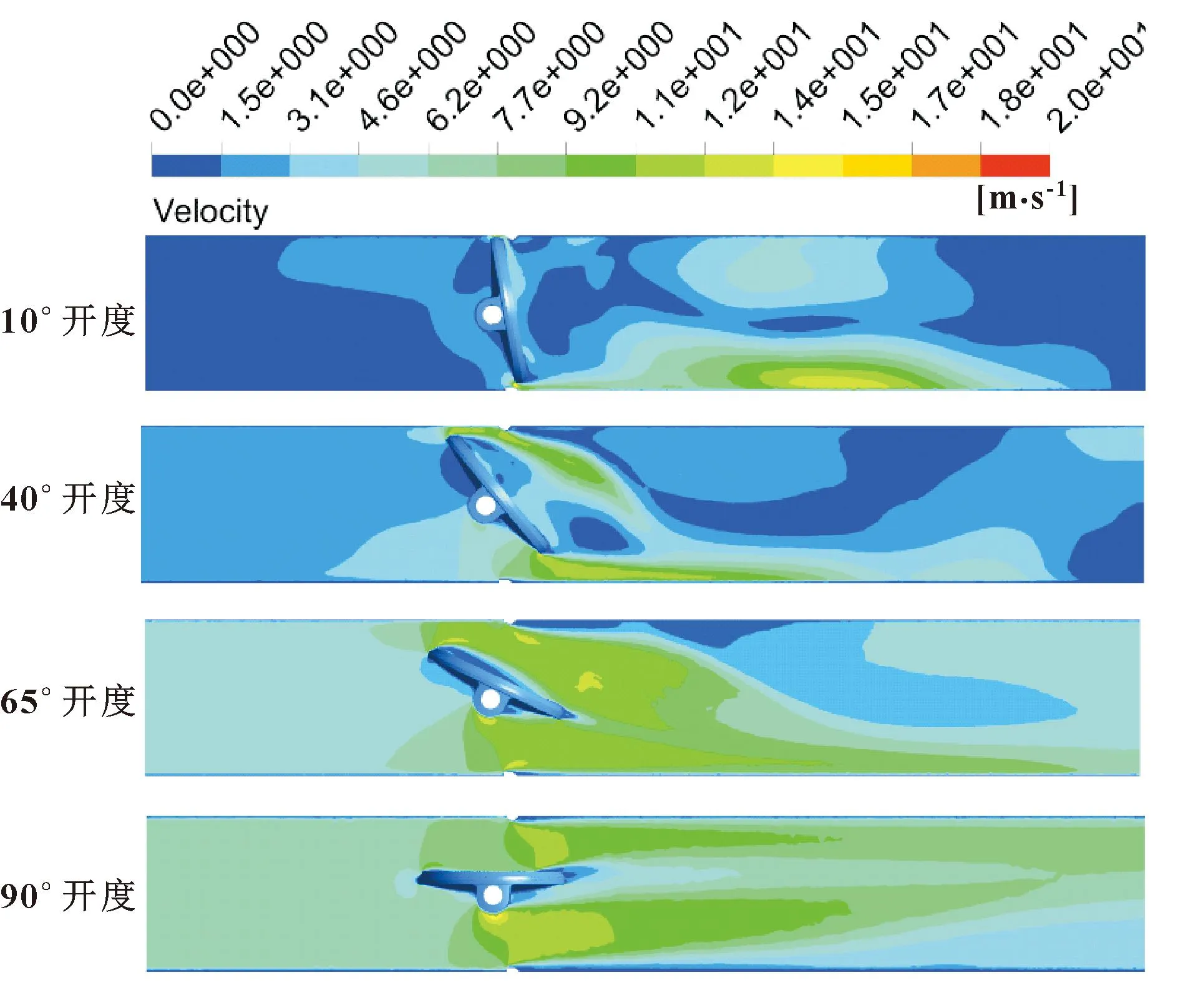
图5 速度云图Fig.5 Speed cloud maps

当入口压力为0.1 MPa时，在10°、40°、65°、90°开度下蝶阀对称面压力云图如图6所示。可以看出：入口段压力始终大于出口段，随着蝶板开度的增大，流动状态更平稳，入口往出口方向的压力变化也更加平缓。除90°开度外，其他开度下蝶板上部的压力大于下部，使蝶板有关闭的趋势。随着开度增大，压差增大，压差产生使蝶阀关闭的力矩，因此蝶阀在此力矩的作用下，阀门开启过程与关闭过程并非简单反过程。

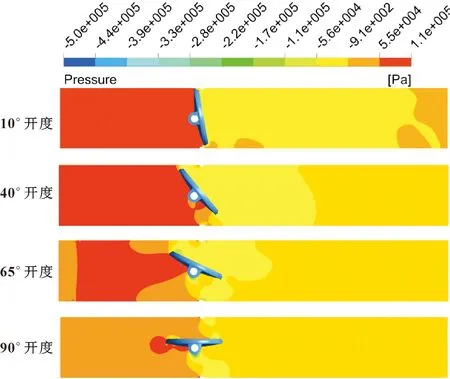
图6 压力云图Fig.6 Pressure cloud maps

2.2 三偏心蝶阀力矩实验与分析

动水力矩测量实验就是将三偏心蝶阀安装在实验管路中，驱动机构采用齿轮齿条式执行机构，通过测量不同开度下阀轴总操作力矩，减去空载时的阀轴力矩，得到不同开度下动水力矩。实验阀门及装置如图7所示。

图7 动水力矩实验Fig.7 Dynamic hydraulic moment experiment

在0.05、0.1、0.3 MPa入口压力条件下，三偏心蝶阀动水力矩及其系数模拟结果、实验结果如表1所示。在同一入口压力的不同开度下，仿真模拟动水力矩的结果与实验结果的变化趋势一致，动水力矩的方向总是与蝶阀关闭方向相同，使蝶阀有关闭的趋势。

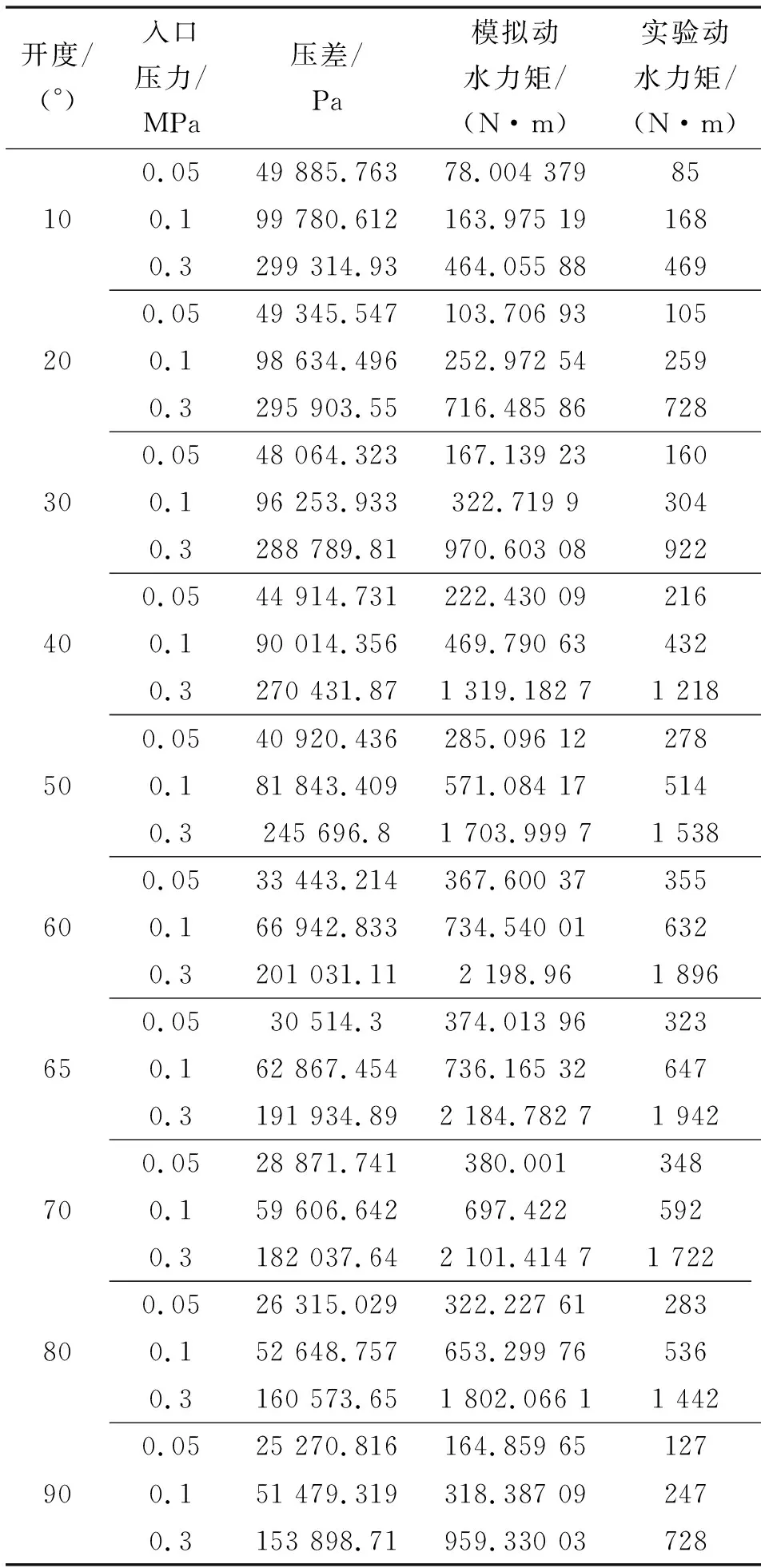
表1 动水力矩结果Tab.1 Dynamic hydraulic moment results

从表1可以看出：随着蝶阀开度增加，动水力矩特性总是呈现先单调递增后单调递减的趋势，在0.05、0.1、0.3 MPa入口压力下，模拟动水力矩分别在70°、65°、60°开度时取最大值。随着压力增大，动水力矩最大值出现的开度在往小开度方向偏移；在不同入口压力下，三偏心蝶阀压差越大，其蝶板上受到动水力矩的数值也相应增大，但是它和开度变化趋势和幅度相同，在0.05、0.1、0.3 MPa入口压力下，在10°～90°开度之间时，动水力矩最大值是最小值的4.5、4.6、4.7倍。

利用公式(4)计算出以动压为基准的阀门动水力矩系数，它随开度增加而减小，不同压差下无明显变化。

由公式(1)-(5)得到不同压差下蝶阀操作力矩随开度的变化曲线。如图8所示：开度越大，动水力矩在总操作力矩中占比越大，0.1 MPa时动水力矩占总操作力矩56.2%，0.3 MPa时为64.83%。阀轴垂直安装的三偏心蝶阀操作力矩，在0.1 MPa压差下开阀过程中最大操作力矩在60°开度时出现，当压差增大，同开度下动水力矩在操作力矩中占比减小。

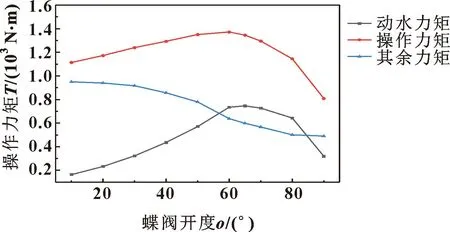
图8 三偏心蝶阀开阀操作力矩(0.1 MPa压差下)Fig.8 Triple eccentric butterfly valve open valve operating torque (under 0.1 MPa pressure difference)

2.3 蝶阀运动状态分析

文中通过研究单作用执行器活塞的位移及速度变化来探究运动平稳性，图9所示为三偏心蝶阀分别在0、0.1、0.3 MPa入口压力下，操作力矩对单作用执行器活塞运动的影响曲线，通过活塞的运动状态反映三偏心蝶板的运动情况。从图9(a)单作用执行器活塞行程中可以看出：当三偏心蝶阀空载没有动水力矩时，单作用执行器在16 s后走完全程，在0.1 MPa动水力矩下需要16.7 s，在0.3 MPa下则需要17.7 s。随着压差的增加，蝶阀的操作力矩随之增大，在此影响下，单作用三偏心蝶阀的开阀动作时间增加，且活塞位移平稳性下降，尤其在操作力矩最大处附近。

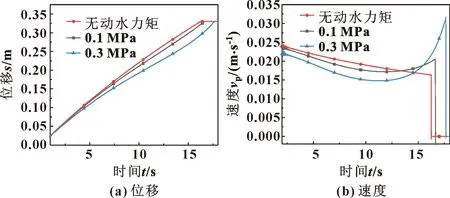
图9 单作用执行器活塞运动状态Fig.9 Single acting actuator piston movement state：(a) displacement；(b)speed

从图9(b)活塞速度中可以明显看出：在开阀过程中，当阀门处于空载无动水力矩状态时，活塞运动速度接近于线性变化，活塞运动平稳，三偏心蝶阀蝶板转动也较为平稳；当蝶阀受到操作力矩作用时，活塞运动呈现先减速后加速的过程，且随着压差的增大，速度变化更加剧烈。研究操作力矩可知：动水力矩在三偏心蝶阀操作力矩中占比较大，导致三偏心蝶阀动作的不平稳性，蝶板转速先减小，当蝶板转过最大动水力矩出现的开度后，蝶板转速快速上升，随着压差增加，动水力矩作用带来的不平稳性变得更加剧烈，0.1 MPa压差下动作时间增加4.4%，0.3 MPa下增加了10.7%。

除操作力矩外，单作用执行器结构参数对开阀动作过程也影响显著，文中探究了执行器气缸尺寸和弹簧刚度对其开阀动作的影响，图10所示为0.1 MPa压差下，不同结构参数对活塞速度的影响。增加单作用执行器活塞直径以及弹簧刚度会使得蝶阀动作过程总时长增加，但能使蝶阀开阀过程更平稳。

3 结论

(1)利用有限元分析软件Fluent分别对10个不同开度下的三偏心蝶阀进行仿真计算，快速准确地获得了包括动水力矩、蝶板压差等阀门内部的流场信息。通过对同一模型不同入口边界条件下动水力矩的研究可知：随着入口压力增大，动水力矩增大，它和开度变化的趋势一致，此蝶阀模型的动水力矩的最大值在60°～75°开度之间，且随着压差增大向小开度偏移，因此蝶阀工作时不能长期处在动水力矩最大的开度。

(2)对三偏心蝶阀在动作过程中操作力矩进行数值计算，得到操作力矩随开度变化曲线，结果表明：动水力矩对蝶阀操作力矩影响较大，尤其是当压差较大时，0.1 MPa时动水力矩占总操作力矩的56.2%，0.3 MPa时为64.83%。

(3)对单作用气动执行器进行气动系统建模，通过活塞的运动状态反映三偏心蝶板的动作特性。结果表明：在0.1、0.3 MPa压差下，三偏心蝶阀动作时间比空载时分别增加了4.4%、10.7%。操作力矩使阀轴速度在整个动作过程中出现先减小后增加的趋势，且随着操作力矩的增大，速度变化更加明显，增加单作用执行器活塞直径以及弹簧刚度可使蝶阀开阀过程更加平稳。