细长轴车削表面粗糙度实验与分析

郭富强，吕凯波，田美霞，王鑫，韩媛，庞新宇

(太原理工大学机械与运载工程学院，山西太原 030024)

0 前言

细长轴类零件在航空航天领域中应用广泛，此类零件的切削加工尺寸精度和表面质量要求较高。变形和振动是影响细长轴类零件加工质量的2个主要因素[1]。表面粗糙度作为机械加工零件重要的几何参数之一，与零件的耐磨性、疲劳强度、接触刚度、配合性质、振动和噪声等密切相关，对机械零件的使用寿命和可靠性有着重要的影响[2-3]。深入研究加工状态及参数对表面粗糙度的影响对于提高细长轴类零件的切削表面质量具有重要意义[4]。

为了预测或监测加工表面质量，需要对加工表面的表面粗糙度进行数学建模，找出影响粗糙度的主要因素。国内外学者针对粗糙度建模开展了大量研究，大体分为理论建模和经验参数建模[5]。TAKASU等[6]建立了考虑振动影响的粗糙度模型，分析了低频率、小振幅振动对表面粗糙度的影响规律。PANDIT、 REVACH[7]基于数据相关系统(DDS)对表面粗糙度进行波长分解，提出了一种预测金属切削表面粗糙度的新方法。KIM等[8]将刀具和工件之间的振动简化为单自由度、单频率的简谐振动，分析了振动频率对表面形貌和粗糙度的影响。安琪等人[9]概括了车削加工过程中表面形貌的影响因素，通过分析各加工成分信息对表面形貌的影响规律，并采用相应信号成分对各加工因素信号成分进行代替，实现了精细表面信号成分的表征和解耦。原路生等[10]基于微织构形成和椭圆振动原理，研究不同转速和进给速度时，微织构的几何尺寸和表面粗糙度的变化规律。陈艳妮[11]建立了切削参数与表面粗糙度之间的响应曲面模型，通过方差分析研究切削参数对表面粗糙度的影响。冯付良[12]研究了轴向进给速度、刀具与工件转速比、刀具倾角和切深等因素对表面形貌和粗糙度的影响规律。

总体而言，基于数据驱动的经验参数建模方法的优势在于不需要深入分析加工过程，只需要找到影响表面粗糙度的各个因素，并将它作为机器学习模型的输入部分，进而预测输出表面粗糙度值；理论建模方法主要基于具有明确切削机制的加工方法建立粗糙度预测模型。本文作者通过几何解析的方法得到车削过程中加工表面理论轴向截面轮廓方程表达式，得出不同切削参数下的理论表面粗糙度值；对比细长轴切削实验中不同加工参数下的零件表面形貌，分析切削状态、切削参数等变化对细长轴加工表面粗糙度的影响。

1 车削表面轮廓理论建模

1.1 截面几何轮廓

工件表面形貌与刀具刀尖半径、切削参数以及刀具和工件的相对振动位移有关。从空间角度来看，工件表面形貌的形成可看作是工件与刀具之间的相对径向位移以进给量为间隔的采样问题，即工件每旋转一周，在被加工表面都会记录下刀具相对于工件的径向振动位移信息[13-14]。

不同的工艺参数与刀具参数的组合所形成的轴向截面轮廓是不同的，在小进给量的条件下，轴向截面轮廓由连续性的圆弧组成，刀具在不同加工状态下形成的截面轮廓如图1所示。

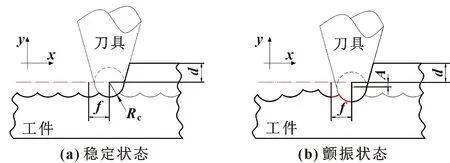
图1 不同加工状态下轴向截面轮廓Fig.1 Axial section contour under different processing conditions：(a)stable cutting；(b)unstable cutting

以首圈截面弧线中心线与工件表面交点为原点，建立如图1所示的坐标系，则第n圈的截面圆弧方程为

y<0

(1)

第n+1圈的截面圆弧方程为

(2)

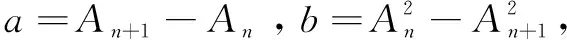
(3)

式中：Rc为车刀顶端圆弧半径，mm；d为切深，mm；f为进给量，mm/r；An、An+1分别为截面处第n、n+1圈刀具径向振动幅度，mm。

将xn代入式(1)中可得到yn，由此得到2段圆弧的交点坐标为(xn，yn)。所以轴向截面的第n个圆弧曲线是从点(xn-1,yn-1)到点(xn,yn)、圆心为((n-1)f,Rc-d-An)、半径为Rc的圆弧。

所以平稳切削即An、An+1=0时，如图1(a)所示，轴向截面的理论方程为

(4)

其中：(n-3/2)f

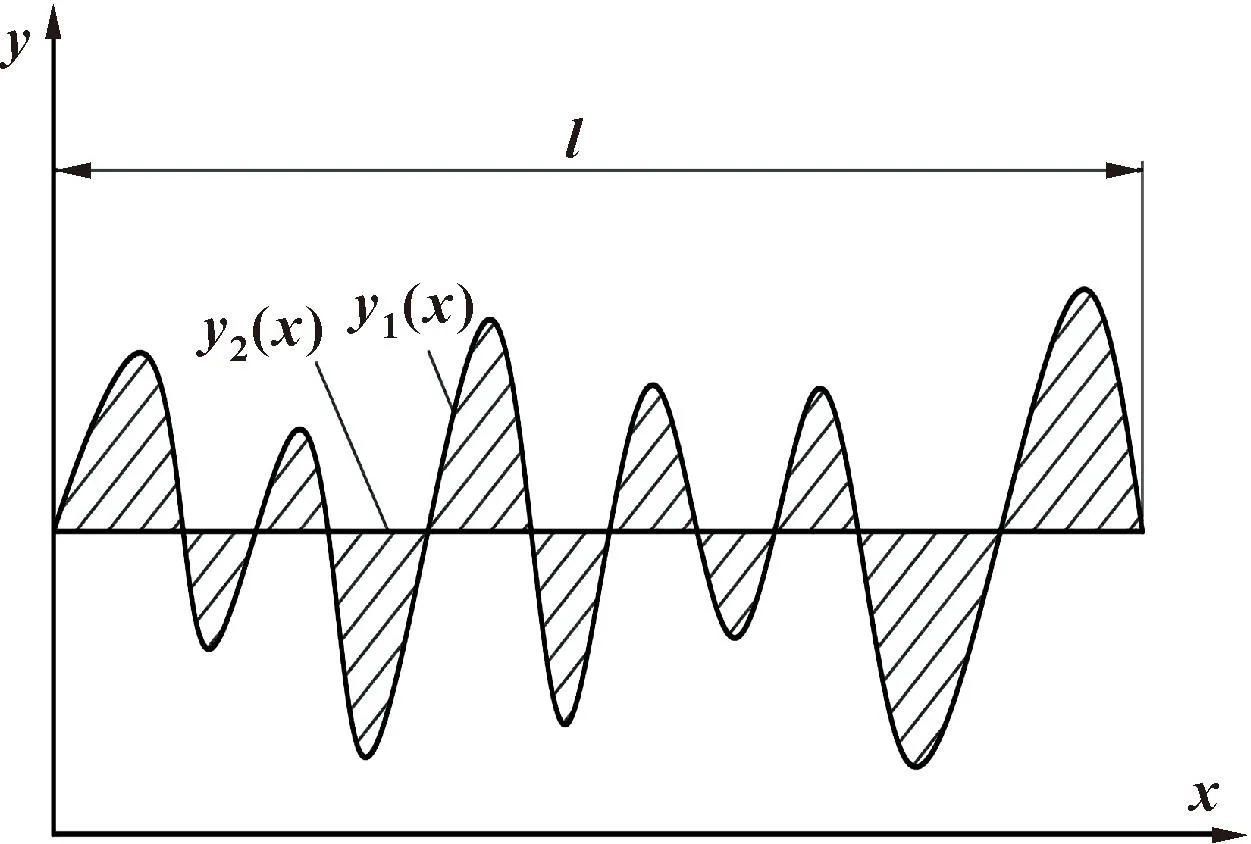
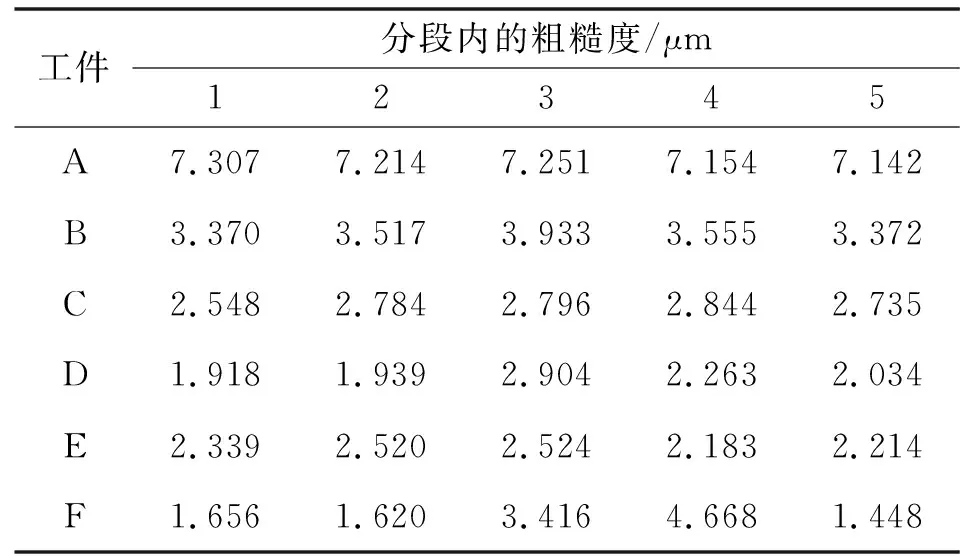
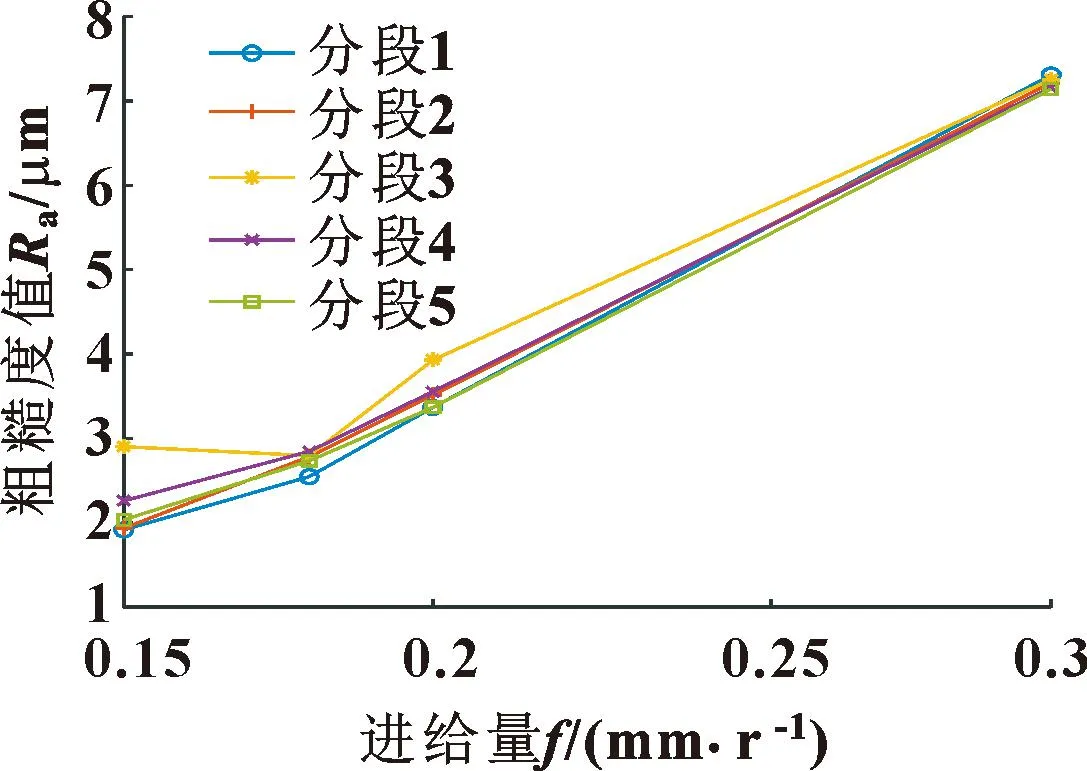
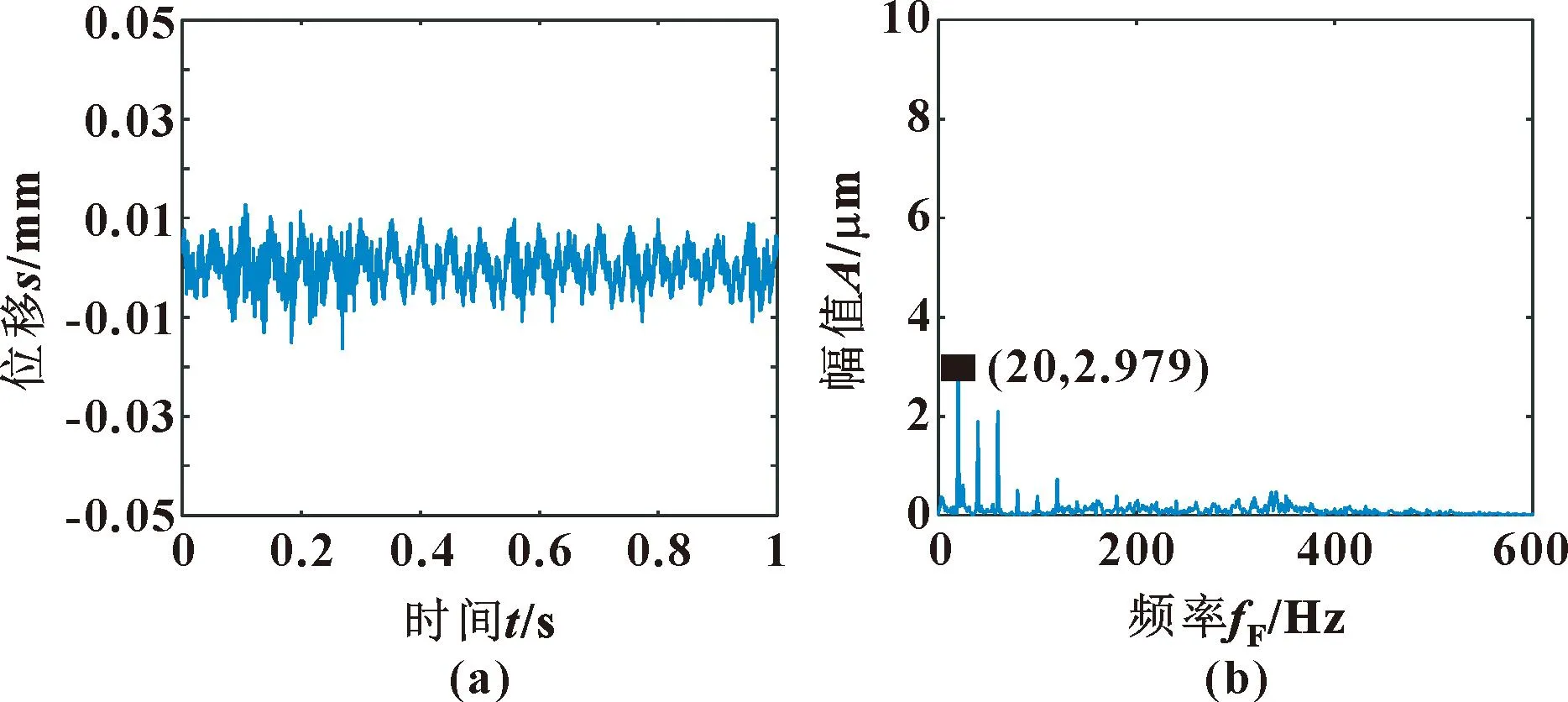
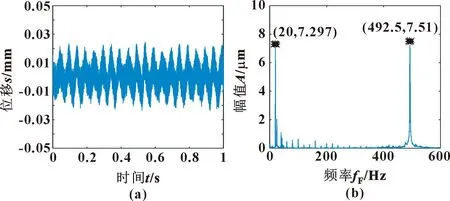
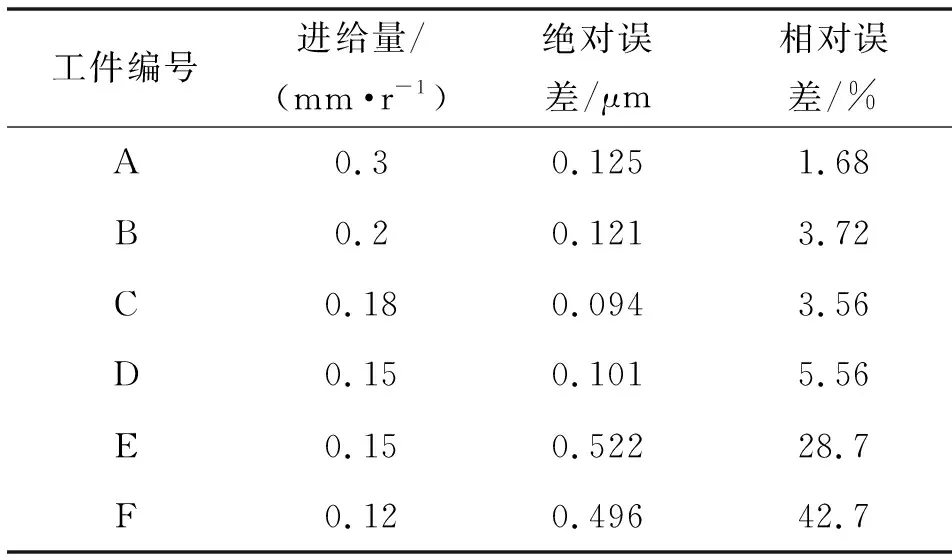
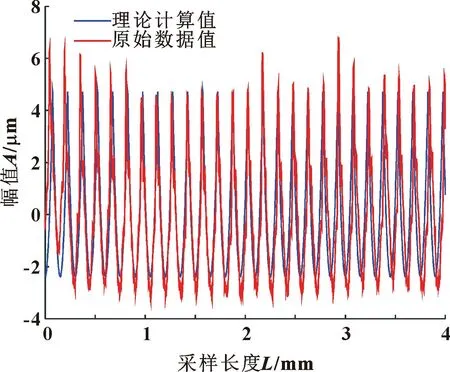
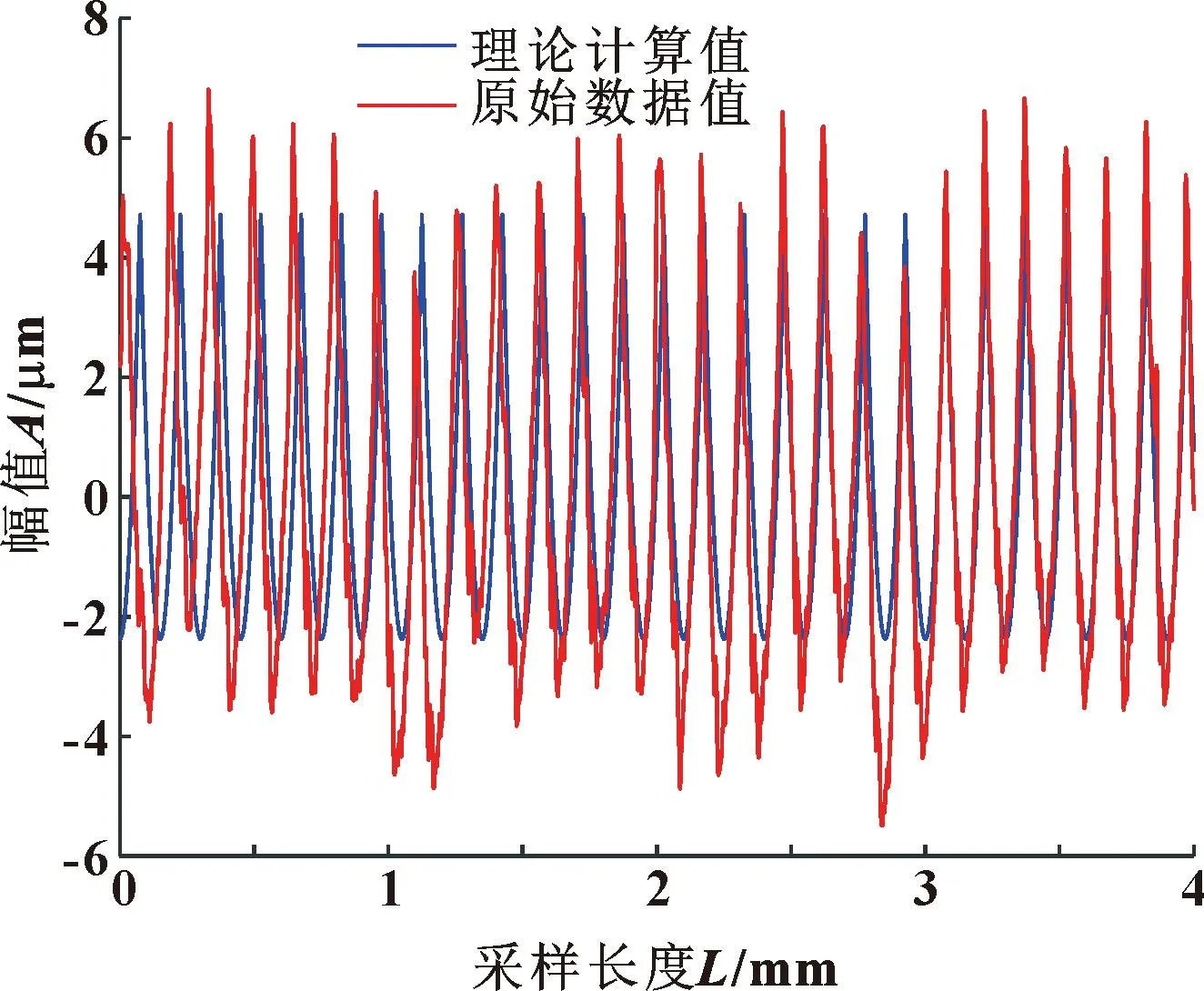
1.2 粗糙度值的计算

表面粗糙度是指加工表面具有的较小间距和微小峰谷的不平度，属于微观几何误差。根据ISO标准，计算粗糙度的方法为：在取样长度内，轮廓线上各点至轮廓中线距离绝对值的平均值，反映轮廓偏离轮廓中线的分散程度[15]，其表达式为

左归丸对免疫性卵巢早衰小鼠血清性激素及IL-6、IL-17水平的影响 …………… 江二喜(8):909

(5)

式中：Ra为粗糙度值；l为采样长度；y1(x)为轮廓线；y2(x)为轮廓中线，如图2所示。

图2 加工表面和轮廓中线Fig.2 Machining surface and contour midline

轮廓中线有2种：轮廓的最小二乘中线和算术平均中线。理论上最小二乘中线是理想的基准线，但实际应用中很难获得，因此文中采用轮廓的算术平均中线代替[16]。

2 表面粗糙度实测与分析

2.1 实验设计

以细长轴作为切削实验对象，选择6组不同的加工参数进行对比实验，其中A-D 4根轴的直径、切削长度以及主轴转速和切削深度完全相同。以进给量为变量，研究其对粗糙度值的影响，工件E和F作为对照组来测试其他因素的影响。实验所用切削参数如表1所示。

表1 切削参数Tab.1 Parameters of cutting process

实验在沈阳机床VIVA TURN2数控卧式车床进行，刀具为型号DCMT11T304 的菱形车刀，圆角半径Rc为0.4 mm，刀具顶角为55°，工件材料为45钢。振动信号由电涡流位移传感器采集，采样频率为10 240 Hz，并通过COCO80数据采集仪保存，采用EDM软件在计算机上进行数据的初步分析处理。

实验台的布置如图3所示。工件一端由卡盘夹紧固定，另一端通过顶尖支承，位移传感器布置在距离顶尖端80 mm处。

图3 车削实验台布置图Fig.3 Turning test bench diagram

2.2 结果分析

通过观察工件表面发现工件F表面存在因颤振而产生的振纹，此种状态下，工件表面不再属于粗糙度研究范围，而是一种表面缺陷。由式(4)绘制6根工件的理论截面轮廓曲线，并根据式(5)计算得到表2所示的理论粗糙度值。

表2 不同切削参数下工件的理论粗糙度值 单位：μmTab.2 Theoretical roughness values of the workpieces under different cutting parameters Unit：μm

采用图4所示MarSurf PS 10表面粗糙度仪对各个工件表面进行粗糙度值测量。测量之前将工件有效切削长度平均分为5段，在每一段内分别测量粗糙度值，其各个分段内的测量值如表3所示。

表3 六根工件各分段内的实测粗糙度值Tab.3 Measured roughness values in segments of six workpieces

图4 实验所用粗糙度仪Fig.4 The profilometer used in experiments

根据式(4)(5)可知：平稳切削状态下的理论粗糙度值的大小只与刀尖圆弧半径和进给量有关，所以同一刀具车削得到的细长轴在相同进给量下的表面理论粗糙度是一定的。从表3中可以看出：实测粗糙度值与理论计算值有一定的误差。其中同一根轴上不同分段内的实际粗糙度值与理论粗糙度值的误差也不相同，原因是实际粗糙度值在加工过程中会受到诸多因素的影响，如工件的振动和变形以及刀具的形状误差和磨损等。

图5 N=1 200 r/min时不同分段粗糙度值与进给量关系Fig.5 The relationship between different segmentation roughness value and feed with N=1 200 r/min

从表3可以看出：在不同切削参数下，没有振纹的5根细长轴整体的粗糙度变化不明显，两端粗糙度相较于中间略小，这与工件两端刚度较大、中间刚度较小相对应，由于中间刚度较小，变形量则会较大，进而粗糙度值也会有所增大。

同时，工件A和C沿轴向的粗糙度变化比较为平缓，而工件B与工件D在中间部分的粗糙度明显高于两端，说明转速为1 200 r/min、车刀运动到中间位置时，进给量为0.3、0.18 mm/r的加工状态比0.2、0.15 mm/r的稳定。而当进给量为0.12 mm/r时，中间部分的粗糙度值产生了明显的突变，表示当时的加工状态产生了变化。这表明进给量、主轴转速与切削位置之间存在一定的匹配关系，进而影响切削加工状态。而当加工状态不稳定时，就会产生如工件F在分段3、4内的振纹。为了进一步研究2种状态下表面粗糙度的不同，通过分析位移信号传感器采集到的信号绘制工件C、F的频谱图，如图6、7所示。

图6 工件C(无振纹)车削表面位移信号时域(a)与频域(b)Fig.6 Time domain(a)and frequency domain(b)of workpiece C (no chatter marks)turning surface displacement signal

图7 工件F(有振纹)车削表面位移信号时域(a)与频域(b)Fig.7 Time domain (a)and frequency domain (b)of workpiece F (with chatter marks)turning surface displacement signal

对比图6、7的时域图可以看出：平稳切削时工件表面振动幅度较小，对应的频域图中的主要成分为主轴转速的轴频及其倍频成分；出现振纹时，工件表面的振动幅度较大，且对应的频域图中除了轴频和其倍频外，还存在一个频率为492.5 Hz的振动信号成分，其频率与工件F的固有频率相近，导致车削过程中产生振纹。

以上分析表明，细长轴的切削加工过程中轴的刚度对表面质量有很大影响，一方面是由于切削力引起轴本身的挠性变形，使得粗糙度中间略大，两端略小；另一方面则是影响切削加工的稳定状态，在一些情况下可能会引起轴的切削颤振，产生振纹，造成粗糙度突变。

所有轴在分段1内受刚性变形的影响较小，可以在这个位置分析其他因素对粗糙度值的影响。计算其理论粗糙度值和实际粗糙度值的误差，如表4所示。已知工件A、B、C、D的主轴转速、切深以及工件本身的参数完全相同，这4根轴在分段1内的理论粗糙度值与实际粗糙度的绝对误差在0.09～0.125 μm内，彼此间差距较小。 工件E与工件D二者的尺寸、进给量和切深相同，但工件E的主轴转速为1 080 r/min，在此情况下，E的绝对误差达到了0.522 μm，比1 200 r/min转速下的工件D高出了很多，这说明细长轴车削时的主轴转速也会对粗糙度产生明显影响。虽然工件F的主轴转速也为1 200 r/min，其直径、长度以及切深与其他工件不同，在0.12 mm/r的进给量，分段1内的绝对误差达到了0.496 μm，相对误差达42.7%。这些都表明理论粗糙度预测模型可能有较大的局限性。

表4 分段1粗糙度误差对比Tab.4 Section 1 roughness error comparison

用粗糙度仪采集到的数据绘制工件D、E的二维形貌(如图8-9所示)，二者尺寸相同，加工参数中只有主轴转速不同，因此对比其实际与理论仿真截面轮廓，可以分析主轴转速造成实际粗糙度值不同的原因。

图8 工件D分段1的二维形貌对比Fig.8 Comparison of 2D topography of workpiece D section 1

通过对比图8和图9发现：理论和实际表面形貌在整体变化趋势以及波峰波谷具体数值之间基本一致。图8中波谷位置处在一条直线上，上下波动不大，而图9中波谷的位置起伏很大，这也是其粗糙度值比图8中高的原因。说明在1 080 r/min的转速下，刀具相对工件表面会有幅度较大的径向振动。在理论粗糙度计算式(1)(2)中，理想条件下An、An+1为0，实际情况中An、An+1的大小很难确定，这也造成了二者有相同的理论值，但实测值相差很大。因此想要提高理论预测值的准确度，必须融合加工过程中刀具的振动信息。

图9 工件E分段1的二维形貌对比Fig.9 Comparison of 2D topography of workpiece E section 1

另外，图8和图9中实际峰谷的底端带有细小的尖刺，这可能是刀具本身的磨损或其他原因造成的。因为在计算理论粗糙度的解析模型中，截面轮廓的弧形截取自标准圆的一部分，而刀尖的顶角与标准圆之间存在着一定的形状误差，这也是理论粗糙度与实际测量值存在误差的原因之一。

3 结论

文中对车削加工表面轴向截面轮廓的粗糙度进行了理论建模，对比分析不同切削参数、加工状态下细长轴切削表面实测粗糙度数据，得到以下主要结论：

(1)在稳定切削状态下，细长轴工件的振动以主轴转频及其倍频为主，加工表面粗糙度受进给量影响最大，进给量越大，表面粗糙度值越高；在细长轴工件轴向不同位置处测量的粗糙度值也略有不同，且中间位置粗糙度值往往大于两端；稳定切削状态且工件刚度较大时，理论粗糙度解析结果与实测结果的误差较小。

(2)在切削颤振状态下，细长轴表面出现有规律的螺旋状振纹，工件的振动中含有与其固有频率相接近的高频振动成分，此时粗糙度理论预测结果与实测结果误差较大。表面粗糙度的影响因素最终通过刀具与工件之间的相对振动而映射到工件表面，所以在理论模型中充分融合工艺系统的振动信息，可进一步提高其预测的准确性。