基于微分平坦的磁悬浮移动平台控制研究

王旭，胡珈宁，李夺，周振雄

(北华大学电气与信息工程学院，吉林吉林 132013)

0 前言

随着时代的发展，传统的滚珠丝杠传动机床逐渐被直线电机驱动的机床所取代。与传统的滚珠丝杠电机相比，直线电机可直接将电能转化为直线运动的机械能，省去了滚珠丝杠传动过程中所消耗的能量。直流直线电机是通电线圈构成的动子由一个软杆支撑，在永磁体生成的均匀磁场中会受到垂直于电流方向的安培力作用，力的大小由安培定则F=BIL确定。如果想要直流直线电机反方向移动，则只需要提供一个反向电流即可[1-2]。但是直流直线电机运动过程中，动子和软杆之间会产生摩擦，从而影响直流电机的精确性[3]。

通过磁悬浮技术将需要支撑的平台悬浮起来，不仅可以消除平台移动过程中的大部分摩擦力而提高移动平台的精确性，还可以降低移动平台和其他机械结构之间的磨损，提高机床的使用寿命[4-5]。传统机床为了降低摩擦力会在部件接触部分涂抹润滑油[6]；而磁悬浮移动平台移动的过程中没有摩擦力，就不需要润滑油[7]，从而大大减少了污染，为工人提供了一个相对洁净的工作环境。

为了使磁悬浮移动平台能够快速、稳定的沿着期望曲线到达预定位置，需要对磁悬浮移动平台的T形动子进行精确控制[8-10]。文献[11]提出了PID算法控制的磁悬浮移动平台，虽然可以使动子最终到达预定位置，但是其算法跟踪性不强，与期望轨迹之间的误差较大，精准性不高。文献[12]提出的模糊PID算法控制磁悬浮移动平台，在PID的基础上增加了模糊推理环节，虽然使动子能更快响应，但无法解决轨迹跟踪的问题。文献[13]提出的滑模控制磁悬浮移动平台，增强了响应速度，但是收敛过早，优化后的精度不高，跟踪性不强，同时参数调节较为复杂。文献[14]提出伪微分反馈(PDF)控制磁悬浮移动平台，相比前几个控制算法响应更快、鲁棒性更强，但还是无法满足轨迹跟踪的要求。

针对算法精准性不足、跟踪性不强、参数调节复杂等问题，本文作者提出基于微分平坦算法控制磁悬浮移动平台。微分平坦算法的精准性和跟踪性远远优于其他算法，并且其参数整度也较为简单。

1 磁悬浮移动平台的模型建立

1.1 磁悬浮移动平台的动力学模型

磁悬浮移动平台是由一个U形定子和一个T形动子组成，如图1所示。T形动子如图2所示，T形动子三端分别缠有一定匝数的线圈，定子为动子提供一个均匀的磁场，当T形动子三端线圈通电之后，T形动子三端会受到安培力作用，通过调整三端通电线圈内的电流大小和方向使T形动子做出不同的运动轨迹。

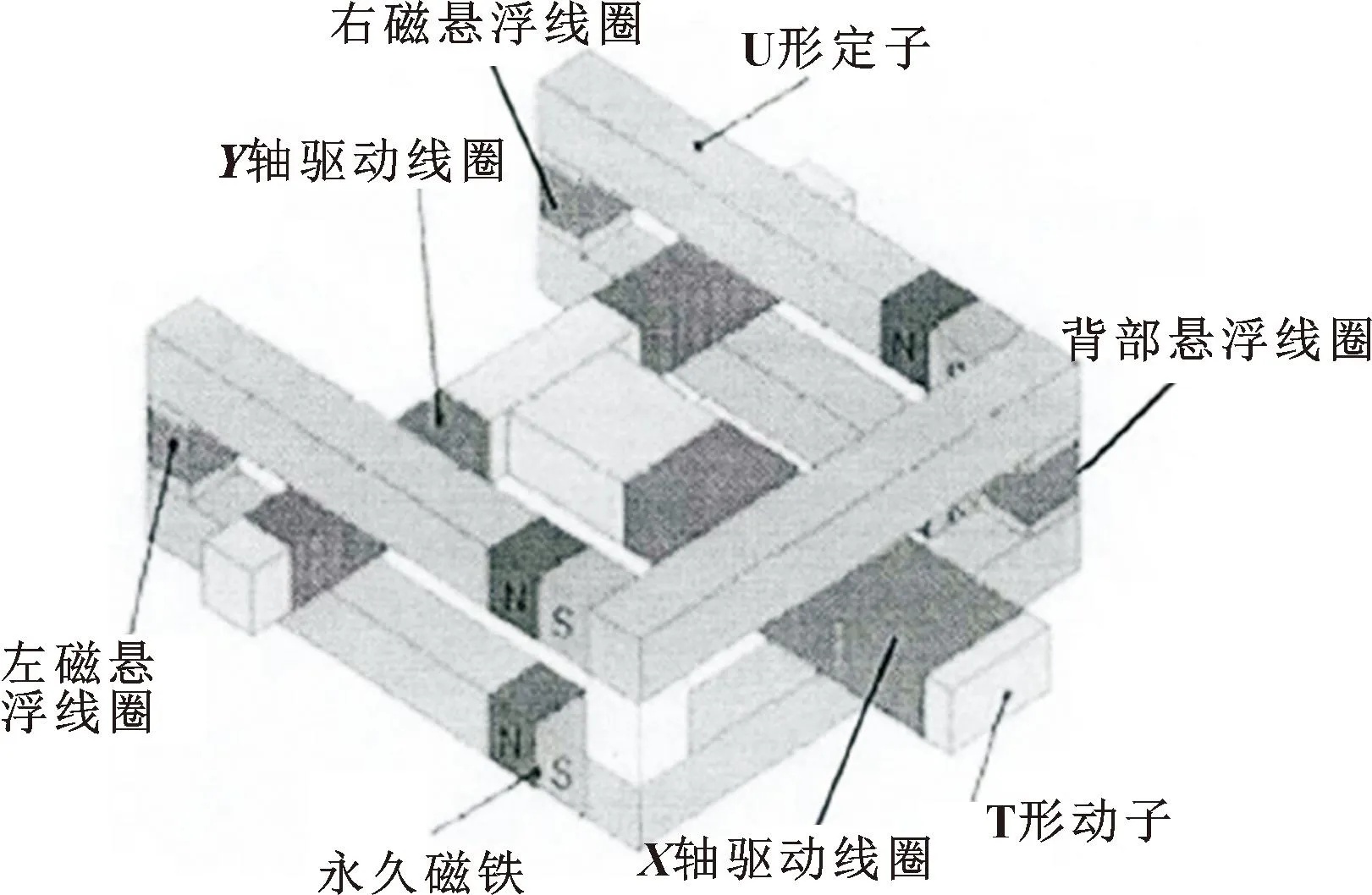
图1 磁悬浮移动平台示意Fig.1 Schematic of maglev mobile platform

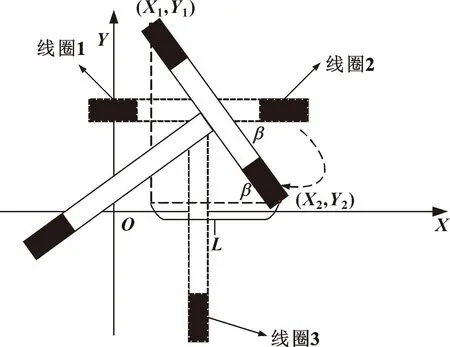
图2 T形动子示意Fig.2 Schematic of T-shaped actuator

1.2 磁悬浮移动平台动子的受力分析

如图3所示，磁悬浮移动平台的动子在水平方向受到3个方向的力，所以动子在水平方向有3个自由度，分别是：沿着X轴方向移动；沿着Y轴方向移动；沿着Z轴方向旋转。动子在旋转过后的位置会与动子的初始位置形成一个夹角β。

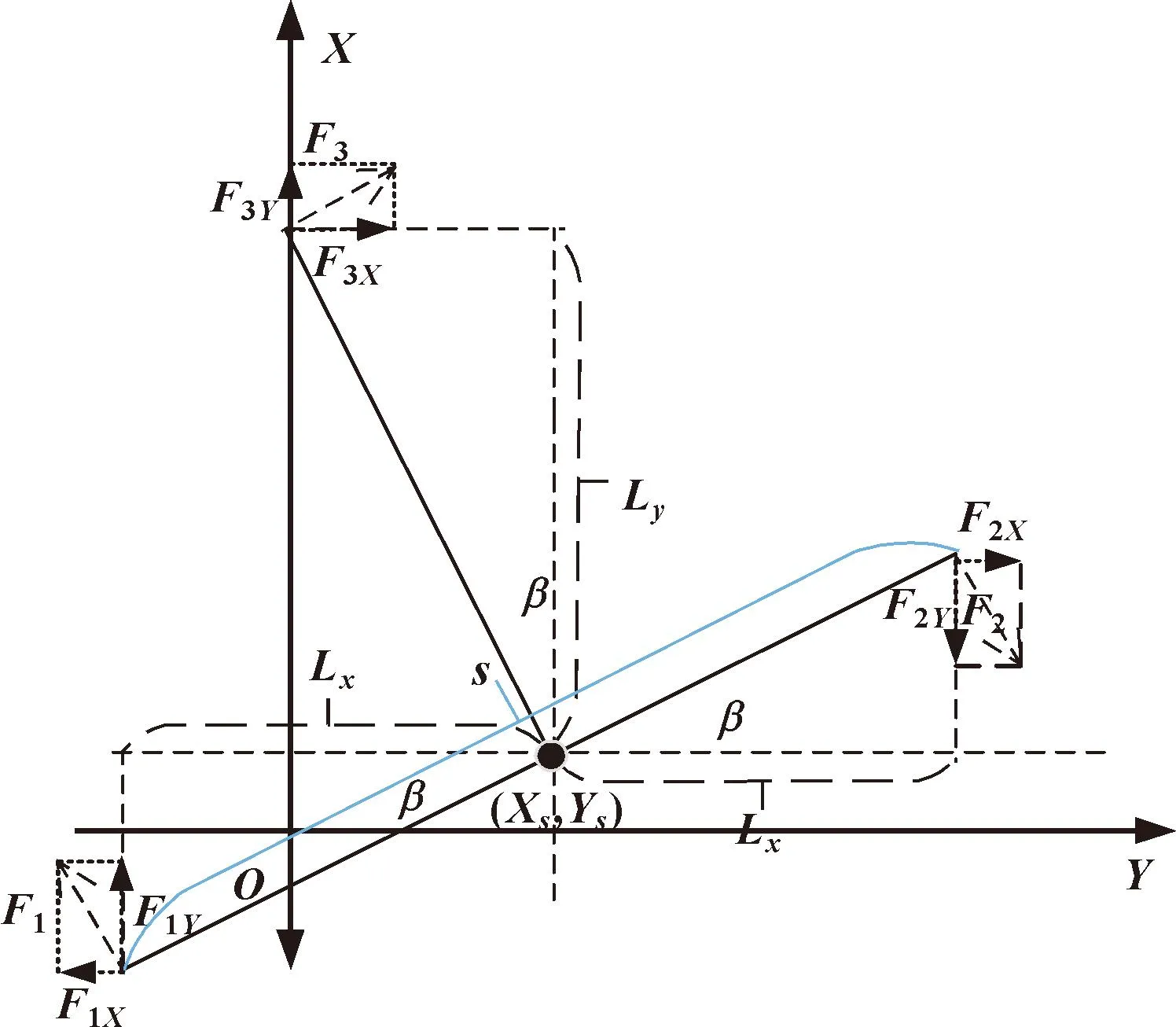
图3 磁悬浮移动平台T形动子受力分析Fig.3 Force analysis of T-type mover of maglev mobile platform

磁悬浮移动平台动子旋转角度β移动公式：

(1)

其中：Y1-Y2为T形动子横向长度；L为横向长度在X轴方向的投影长度。

如图3所示，T形动子所受到的3个力可以根据三角函数分解成沿X轴方向的力和沿Y轴方向的力。每个力分解之后的形式为

(2)

其中：F表示矢量；f表示标量；β表示T形动子的偏移角度。

可以结合以下动力学公式化简上述公式：

(3)

其中：F是力；v是速度；s是位移；m是动子质量；M是力矩；J是转动惯量；α是角加速度。

将式(3)代入式(2)化简得到：

(4)

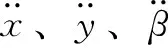
其中：f1、f2、f3是3个水平方向的力；u1、u2、u3是输入电压。由图4可知3个水平力的表达式为

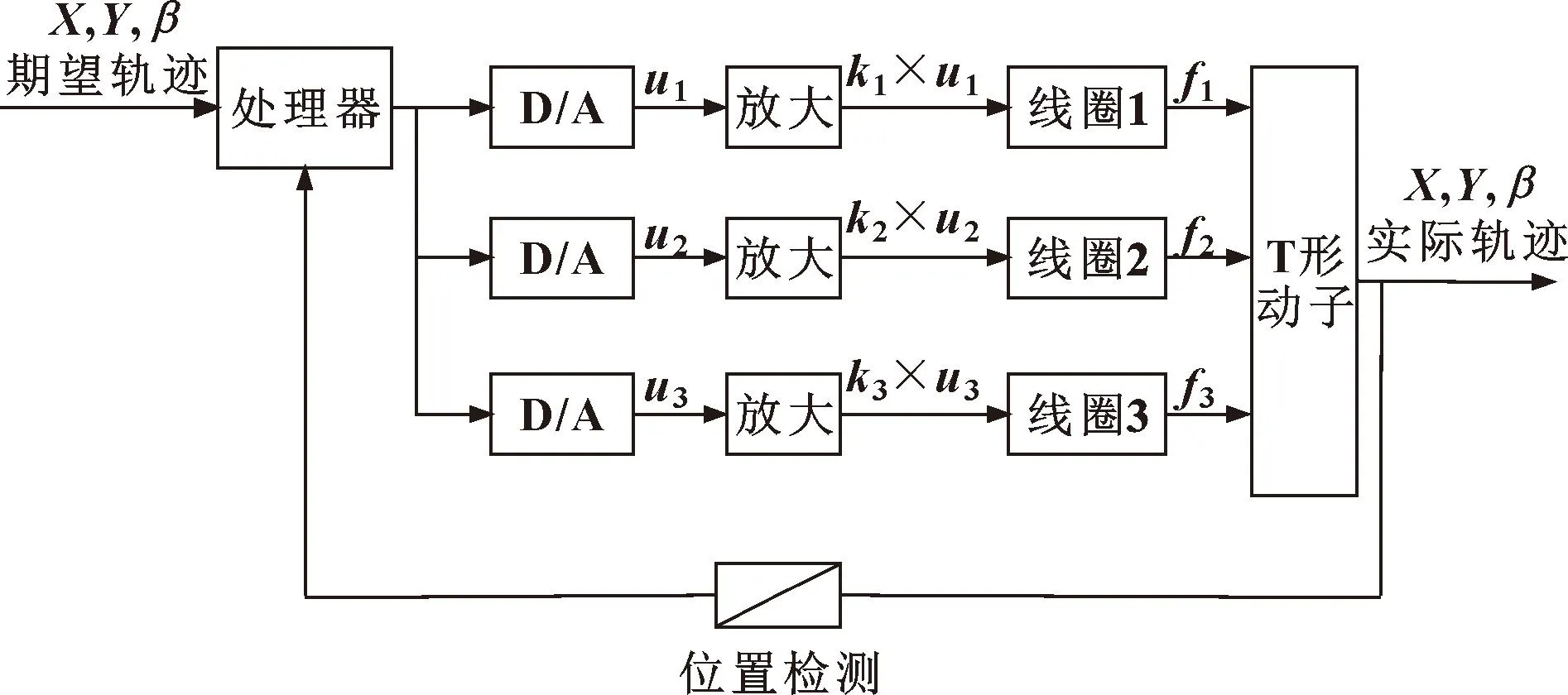
图4 T形动子水平移动控制原理Fig.4 Principle of horizontal movement control of T-type movable actuator

(5)

因为输入电压通过放大之后变成电流，然后电流输入各个线圈产生各个方向的水平力，所以k1、k2、k3为比例系数(A/V)。将式(5)代入式(4)中，化简得到：

(6)

2 微分平坦理论与微分平坦性验证

2.1 微分平坦理论简介

微分平坦理论是在逆动力学原理的基础上提出来的，理论上微分平坦理论应该被应用于线性系统，但是目前微分平坦理论更广泛应用于非线性系统。微分平坦理论(Differential Flatness)最早作为微分代数的概念被提出，后来由FLIESS、RATHINAM和MURRAY等经过一系列的研究后应用于动力学问题[15-16]。微分平坦理论指出了非线性系统动力学特征的存在性，理论上如果该线性系统满足某种条件并且选择合适的微分平坦输出，就可以将非线性系统转化为线性系统。换句话说，如果能找到一组合适的平坦输出量，并且系统中的所有状态变量和输入变量都可以由这一组平坦输出量以及平坦输出量的各阶导数表示出来，那么这个系统就是微分平坦系统[17]。目前微分平坦理论被广泛地应用于轨迹跟踪、功率跟踪等。由于微分平坦系统的输入变量和状态变量可以由平坦输出量以及其导数变换得到，那么根据期望的平坦输出轨迹，可以直接获得无差的状态变量和输入变量。如果微分平坦系统用公式可以更准确地表示为

(7)

如果状态变量和输入变量能满足下列条件：

(8)

则可以称此非线性系统为微分平坦系统。其中r和t都是整数，表示导数阶数。由于非线性系统选取的平坦输出量并不唯一，所以状态变量和输入变量也可能不同。

2.2 磁悬浮移动平台微分平坦性验证

根据式(6)得到磁悬浮移动平台状态方框图如图5所示。

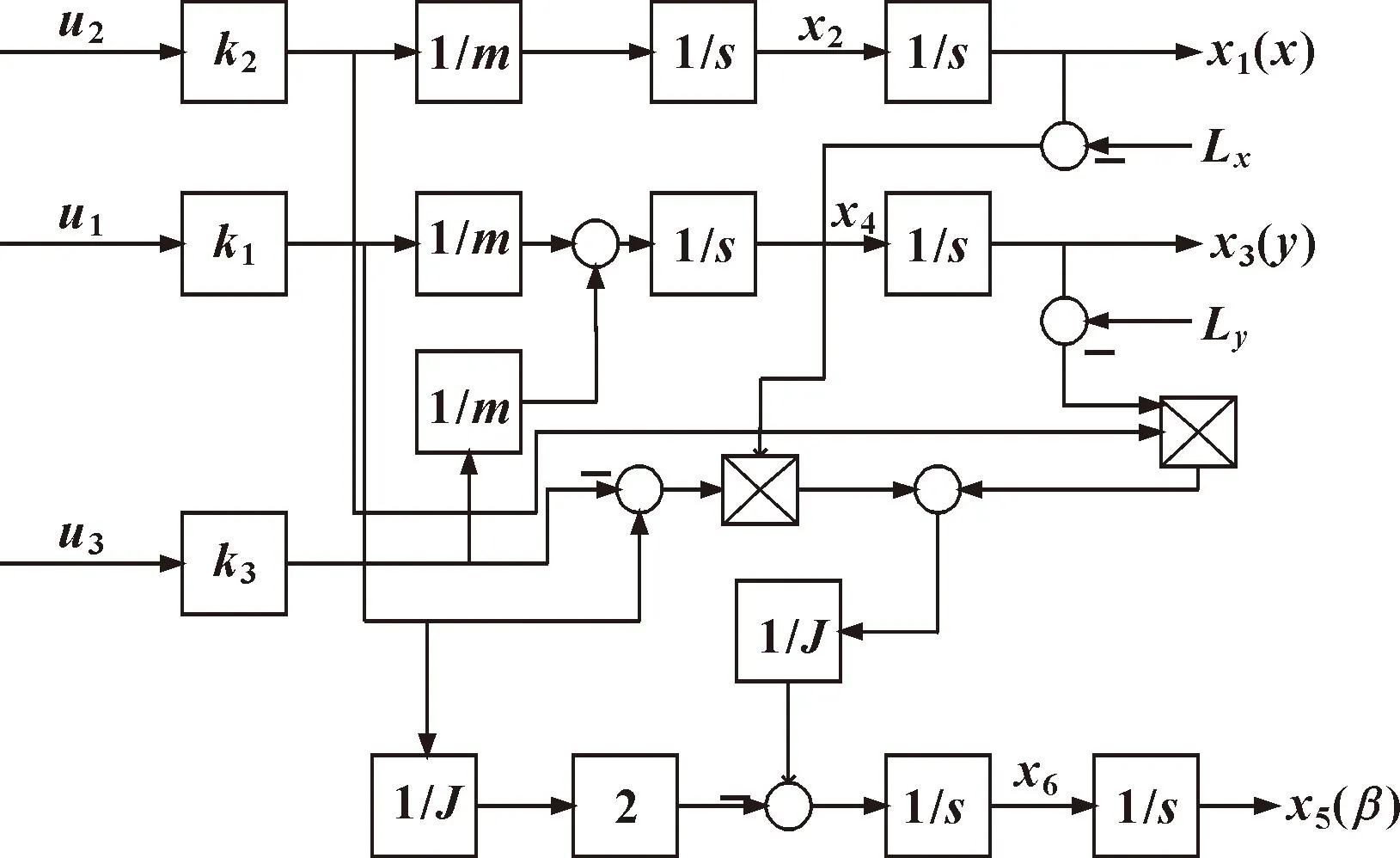
图5 磁悬浮移动平台状态方框图Fig.5 Block diagram of maglev mobile platform status

系统的状态方程为

(9)

其中：vx是动子沿X轴方向运动的速度；ax是动子沿X轴方向运动的加速度；vy是动子沿Y轴方向运动的速度；ay是动子沿Y轴方向运动的加速度；ω是动子旋转的角速度；α是动子旋转的角加速度。

平坦系统的输入矩阵为

(10)

由图5可知状态变量可由输出变量表示为

(11)

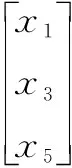
(12)

由此可见，该系统所有的状态变量都可以由该系统的输入变量以及其导数表示。

由式(6)可知输入的变量可由输出变量表示为

(13)

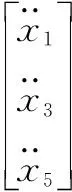
(14)

由此可见，该系统所有的输入变量都可以由该系统输出变量的二阶导数表示。综上所述，输入变量和状态变量都可以由输出变量以及其导数表示。

3 磁悬浮移动平台微分平坦控制系统设计

磁悬浮移动平台是一个微分平坦系统，并且成功地选出一组较为合适的平坦输出值。根据前面的公式和微分平坦验证可知，磁悬浮移动平台控制系统由前馈控制组成，但该系统在实际运行过程中实际输出的轨迹会与期望轨迹产生偏差，所以还需要加一个PI控制对误差量进行补偿。前馈控制首先需要根据式(8)生成期望的前馈控制量：

(15)

式中带有“*”的值表示期望值。

实际输出轨迹和期望轨迹的误差为

(16)

输入变量的误差为

(17)

为了消除控制过程中产生的误差，使磁悬浮移动平台更好地跟踪期望的轨迹，需要加入一个PI控制，PI控制反馈补偿量为

(18)

式中：kp、ki、kq、ko、ke、kf为PI控制参数。因为磁悬浮移动系统有3个自由度，所以需要用3个PI控制，并且参数也不同。

实际微分平坦输入控制量为

(19)

实际微分平坦输控制量由前馈控制量和反馈控制量共同组成。基于微分平坦的磁悬浮移动平台系统控制原理如图6所示。

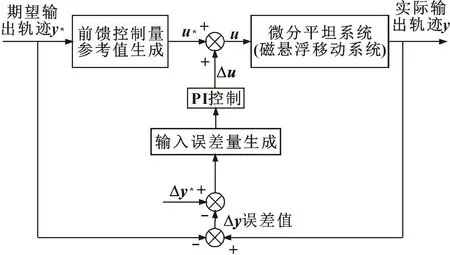
图6 基于微分平坦的磁悬浮移动平台系统控制原理Fig.6 Control principle of maglev mobile platform system based on differential flatness

4 微分平坦参数化与轨迹规划

通常情况下，轨迹规划问题就是最优控制问题，最优控制有以下形式：

(20)

微分方程需要满足约束方程：

(21)

同时需要满足以下约束方程：

(22)

式(21)(22)是轨迹规划最优问题的约束方程。直接求解轨迹规划最优问题非常困难，除了上述约束方程之外还有动力学微分公式，常规的求解方式无法轻易求出，所以需要将平坦输出量参数化，把求解轨迹规划最优问题简化。平坦输出变量参数化之后还可以降低系统的维数，将上述选取的平坦输出量y参数化后就变成了y=(y(t1),y(t2),y(t3),…,y(tn))。而且由微分平坦系统的特性可知，系统的状态变量和输入变量都可以由其输出变量表示出来，所以可以明显降低系统的维数。通常情况下，系统输出变量的维数和输入变量的维数是一致的，系统的状态变量维数高于系统输出变量。例如上述选取的磁悬浮移动平台系统的状态变量是6维，而系统的输出变量和输入变量都是3维。

为了规划一条轨迹，需要将平坦输出量参数化为合适的时间函数。比如所有的平坦输出y都可以参数化为

y(t)=Aijφj

(23)

式中：φj为基函数，该系统所有的平坦输出变量都可以由这些基函数自由组合之后表示出来。基函数有很多种类型：多项式函数、三角函数、高斯函数、三样条以及B-样条。选取基函数时需要考虑基函数的阶数，一般参考状态变量和输入变量在平坦输出变量表达时出现的最高阶数。将系统出现的最高阶数设为J，一般基函数的阶数不低于J。

假如设动子的期望轨迹为y=x2，将平坦输出x参数化为一次函数x(t)=t2，因为磁悬浮移动平台系统出现的最高阶数为2，所以此函数满足条件。则平坦输出可以表示为

(24)

根据式(6)(9)将输入变量和状态变量分别表示为

(25)

(26)

5 仿真分析

通过MATLAB/Simulink搭建磁悬浮移动平台微分平坦控制系统，磁悬浮移动平台的各个参数如表1所示。将微分平坦输出量参数化规划为一条轨迹，表达式为：y=x2。通过4个方面分析磁悬浮移动平坦动子的运动轨迹，仿真波形如图7-10所示。

表1 磁悬浮移动平台参数Tab.1 Parameters of maglev mobile platform

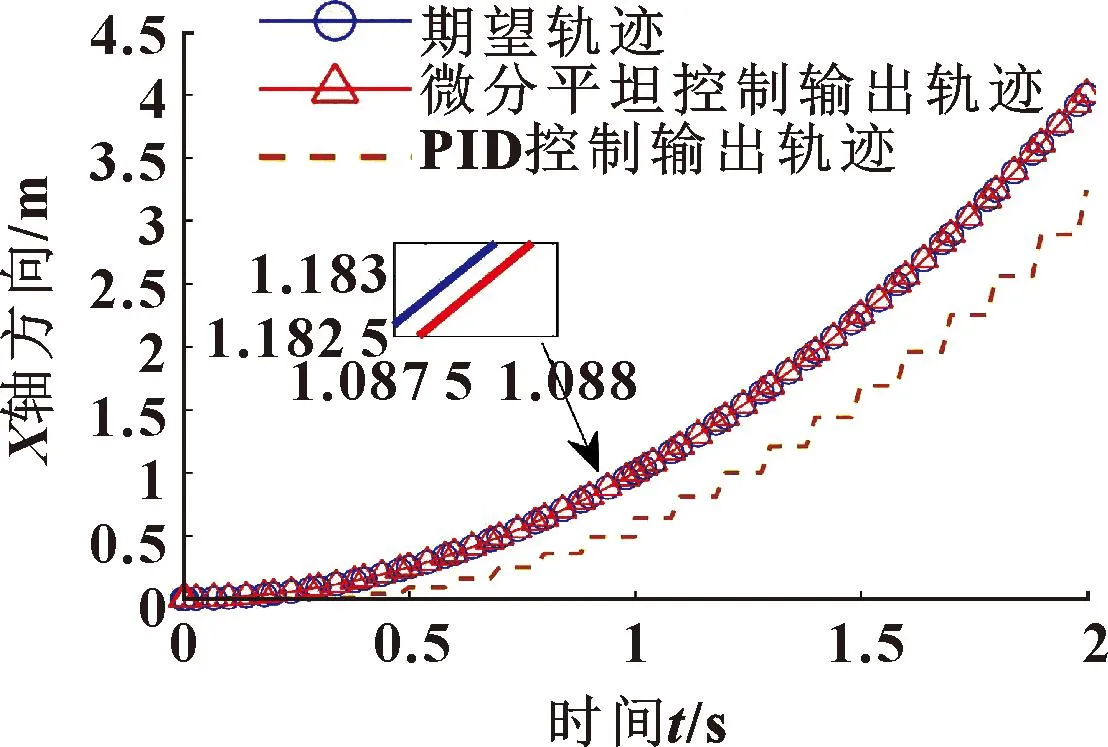
图7 动子沿x方向随时间移动波形(期望轨迹y=x2)Fig.7 Waveforms of mover moving with time along the

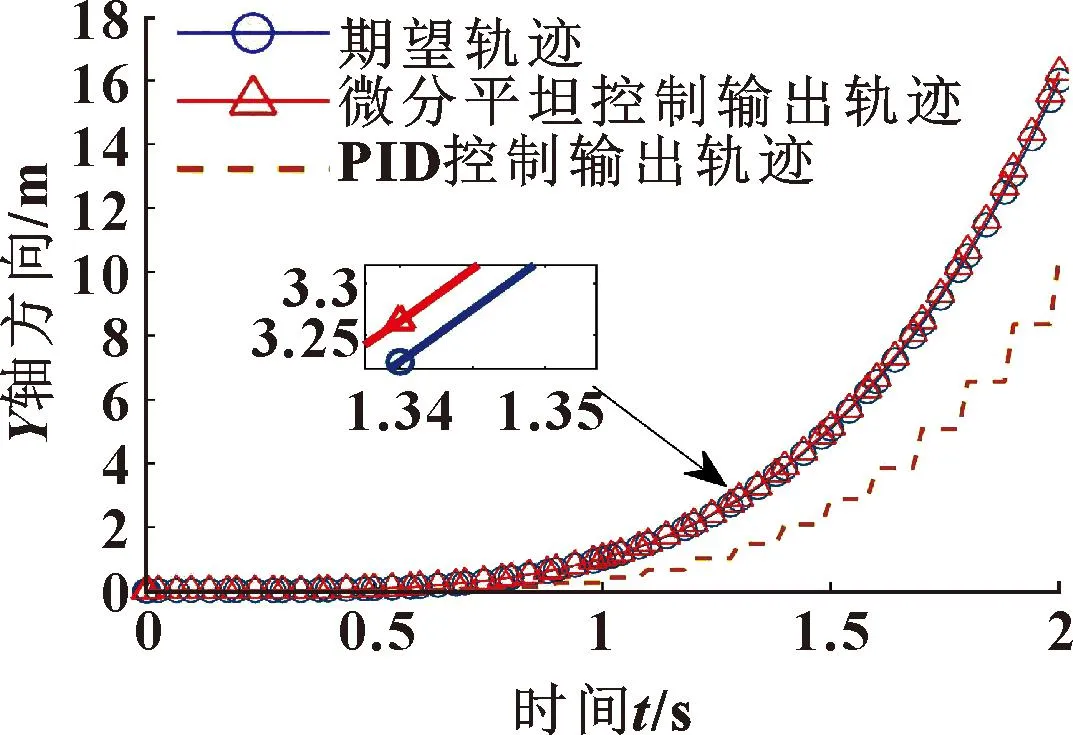
图8 动子沿y方向随时间移动波形(期望轨迹y=x2)Fig.8 Waveforms of mover moving with time in y direction (expected trajectory y=x2)

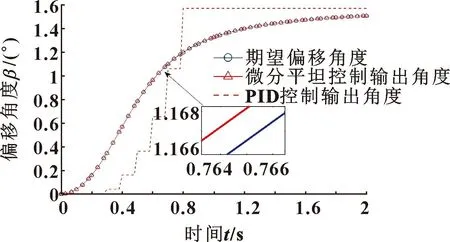
图9 动子偏移角度随时间移动波形(期望轨迹y=x2)Fig.9 Waveforms of mover offset angle moving with time (expected trajectory y=x2)

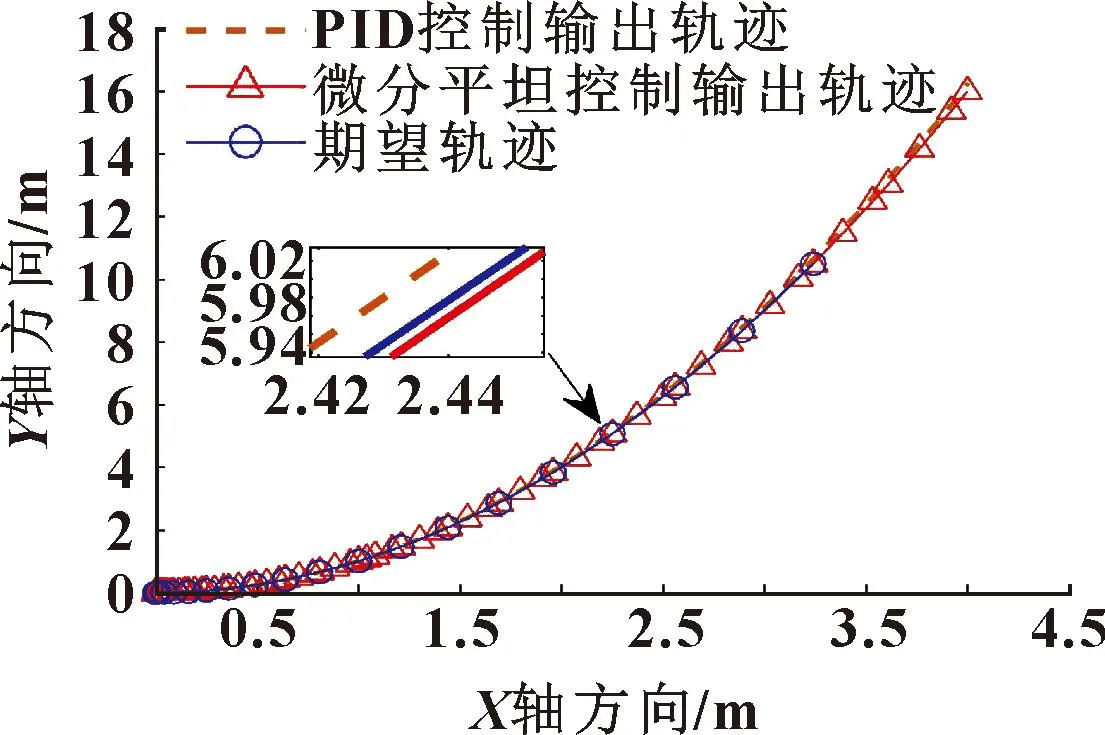
图10 动子实际移动轨迹波形(期望轨迹y=x2)Fig.10 Waveforms of actual moving track of mover (expected trajectory y=x2)

xdirection (expected trajectoryy=x2)

通过图7-10可知：磁悬浮移动平台通过微分平坦控制，动子的移动轨迹几乎跟随期望轨迹；而通过PID控制磁悬浮移动平台，动子的移动轨迹与期望轨迹之间的误差较大。说明微分平坦控制比PID控制更为精准，可靠性更强，尤其是在加工允许误差较小的零件时。

为了验证磁悬浮移动平台微分平坦控制系统的可靠性，需规划一条新的轨迹。为了更直观地对比微分平坦轨迹与期望轨迹以及PID控制的轨迹，选取一条较容易观察的轨迹曲线。选取的轨迹曲线表达式为：y=sin2x，因为该表达式为一阶，所以令x(t)=t即可。其他参数化后的表达式同上述方法，这里不再一一列出。仿真之后的波形如图11-14所示。

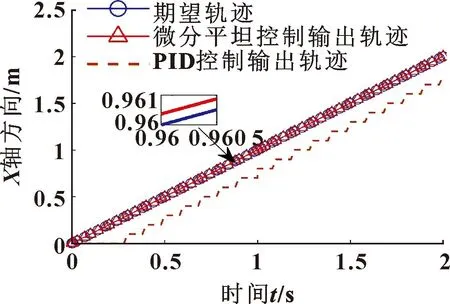
图11 动子沿x方向随时间移动波形(期望轨迹y=sin2x)Fig.11 Waveforms of mover moving with time along the x direction (expected trajectory y=sin2x)

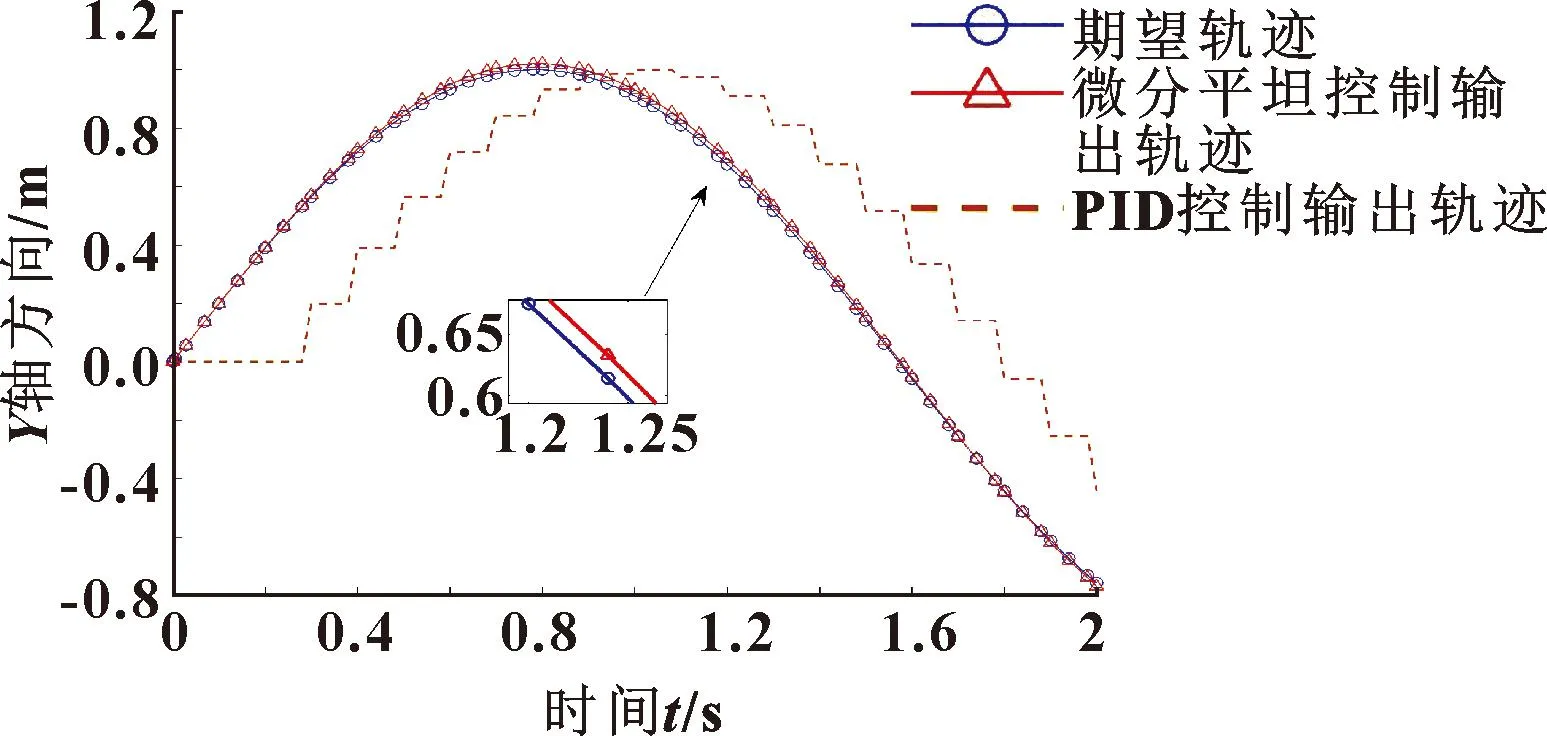
图12 动子沿y方向随时间移动波形(期望轨迹y=sin2x)Fig.12 Waveforms of mover moving with time in y direction (expected trajectory y=sin2x)

图13 动子偏移角度随时间移动波形(期望轨迹y=sin2x)Fig.13 Waveforms of mover offset angle moving with time (expected trajectory y=sin2x)

图14 动子实际移动轨迹波形(期望轨迹y=sin2x)Fig.14 Waveforms of actual moving track of mover (expected trajectory y=sin2x)

由图11-14可知：当期望轨迹为正弦函数时，可以清楚地观察到微分平坦控制的磁悬浮移动平台动子会更精准地跟随期望轨迹移动，而PID控制的磁悬浮移动平台动子则会偏离期望轨迹。从宏观来看，磁悬浮移动平台动子整体的移动轨迹几乎重合，但放大之后发现微分平坦控制的磁悬浮移动平台动子的移动轨迹更加贴近期望轨迹。

6 结论

文中构建了磁悬浮移动平台的数学模型，通过数学模型结合动力学公式得出磁悬浮移动平台系统的状态空间表达式。结合微分平坦控制原理验证了磁悬浮移动平台是微分平坦系统；对微分平坦输出量进行参数化和轨迹规划。相对于传统控制系统给定一个位置后让磁悬浮移动平台动子快速到达预定位置而言，微分平坦控制的磁悬浮移动平台系统不仅能让动子快速到达预定位置，还能让动子按照期望的轨迹达到预定位置。相对PID控制的磁悬浮移动平台系统而言，微分平坦控制的磁悬浮移动平台系统中动子更接近期望轨迹曲线，更精准，可靠性更强。所以文中提出的微分平坦控制磁悬浮移动平台系统具有实用性。