基于随机几何的变电站无线通信信道模型

黄鑫, 马瑜, 李芹, 李文猛, 李朗, 韩东升*

(1.南瑞集团有限公司(国网电力科学研究院有限公司), 南京 211006; 2.华北电力大学电子与通信工程系, 保定 071000)

电力系统多场景、多业务、多指标的通信需求对变电站中的通信质量和效率有着更高的要求。有线通信设备虽然具有较好可靠性但在变电站内全覆盖铺设的复杂度和成本较高,同时难以满足如巡检机器人[1-2]、无人机(unmanned aerial vehicle,UAV)[3-5]等移动通信设备在变电站的使用需求。无线通信方式由于其无线通信终端部署灵活,应用便捷,使在变电站室外通信不再受到有线通信距离和成本的限制,近年来被广泛应用于电力系统中。

对变电站室外无线信道特性的准确认知,是构建变电站无线通信系统的基础。首先,由于变电站室外存在变压器、塔杆和建筑物等大型设备,无线信号必然受到这些设备和建筑的反射、散射、折射等,产生大量多径效应,对变电站室外无线通信质量产生较大影响;其次,变电站室外的移动终端通信将产生多普勒效应,同时无线信道具有时变性和非平稳性。这些因素共同影响着变电站室外通信的有效性以及巡检的可靠性。由于上述分析不能完整的描述变电站室外无线信道特性。因此,需要对典型变电站室外通信场景进行信道建模。

目前,无线通信信道建模的主流方法有射线追踪法、统计法和随机几何法。文献[6]使用射线追踪建模并结合机器学习算法,以麦克斯韦公式为核心对信道测量的参数进行处理,较为精准地推导出信道的离开角(angle of departure,AOD)、到达角(angle of arrival,AOA)、路损和时延[7-10],提高了模型的实时性和准确性,但是在面对变电站等复杂场景时,测试量的复杂度和成本将会大幅增加。文献[11]采用一种高精度的网络扫描仪器对变电站复杂环境下的所需频率范围信号进行扫描,从而搭建在电网复杂电磁环境下的经验模型,模型的大尺度衰落和小尺度衰落、网络延迟、相干带宽等相应参数都表现出与传统模型的不同之处,该研究成果为无线通信在变电站这种特殊的通信环境下的信道建模工作提供了很好的启发,但对测量工具的精度有较高的要求,不能到达精确度和复杂度的折中;文献[12]分别用射线追踪法、统计法、随机几何法对室外小区、无人机城区、高铁山区3种场景进行信道建模,验证了随机几何建模法能更好地适应具有非平稳性以及快速变化的时变信道,对变电站移动终端无线通信场景的非平稳信道建模提供了启发。文献[11-12]采用的射线追踪法和统计法均需对场景信道进行实际测量,造成复杂度高、成本大的问题。文献[13]通过实际测量和数学建模,利用智能电网的变电站中接收信号强度值来推导此场景下的路径损耗模型,优化变电站的网络规划,降低部署、运营和维护成本,同时提高性能,但在非平稳信道中应用具有较大的局限性,信道测量的复杂度和成本都会大大提高。

随机几何建模法将实际通信场景抽象为简单的几何图形,根据几何关系推导数学模型,基于理论对特定场景信道特性进行分析,减小了建模的复杂度和成本,同时在非平稳信道建模上具有优越性,故被广泛地应用在各种场景下的无线信道建模中。文献[14]基于V2V场景,提出了一种将椭圆和圆环这两种规则图形结合的双环双同焦椭圆2D随机几何模型,该模型在基础平面图形下通过结合和叠加,使搭建的模型能更贴合实际场景,达到优化模型的目的;文献[15]将基于几何的随机模型与航空随机机动性模型(RMM)[16]结合起来,提出了同轴多圆柱嵌套随机几何模型,推导了无人机通信场景的非平稳模型的相关参数和统计特性;文献[17]主要针对散射环境高速变化的高铁隧道时变进行建模,将隧道抽象为平躺的空心圆柱体,散射体随机分布在圆柱体表面,通过研究该模型下的非平稳信道特性和信号质量来指导高铁在隧道中的通信。以上圆柱形的随机几何模型为本文提供了参考,但由于变电站场景复杂,各自电气设备排布密集,与以上V2V和高特场景有较大差距,单纯用圆柱并不能完整描述变电站室外散射环境,所以需要对这种圆柱模型进行优化和改良,已满足搭建变电站室外随机几何模型的需求。

以上文献对于V2V、UAV通信和高铁通信场景的随机几何建模方法、模型结构进行了研究和创新。可以看出,随机几何法对时变的非平稳信道建模有较好的优越性,在满足模型普适性和准确性的情况下,简单的抽象几何图形能够减小建模的复杂度。因此,随机几何建模法在复杂变电站场景的非平稳无线信道特性研究吸引了一些学者的注意。文献[18]研究了变电站室内5G巡检机器人通信场景,基于随机几何法,将变电站室内散射环境抽象为一个平面,通过推导模型的ST-CF[19]、ACF[20]、CCF[21]函数,研究了信道的自相关、互相关特性以及莱斯因子对信道特性的影响,为用随机几何法在变电站场景下进行信道建模提供了思路,但该文献抽象几何模型较为简单,不适用于设备种类多样、排布密集、结构复杂的变电站室外场景。因此,采用随机几何建模法对变电站室外场景抽象建模,研究其无线通信场景的信道特性,推导数学模型并仿真验证。

现针对变电站地处偏远、电气设备材质多样和其错综复杂的位置关系等特点提出圆形栅柱随机几何模型,并将其分为LOS子区和NLOS子区。采用冯·米塞斯(Von Mises fisher,VMF)[22]分布来刻画散射体分布状况,并用数学几何法推导出模型的ST-CF、CCF、ACF公式和多普勒功率谱密度,推导出仿真模型。用MATLAB进行仿真,验证参考模型的正确性,分析在影响信道模型的关键因素,以优化模型并对变电站室外无线通信提出指导和建议。

1 系统模型

本文研究考虑一个变电站室外场景,如图1所示。该场景散射成分复杂,除了大型设备如变压器、塔杆、电缆等,一些建筑物对信号传播也会造成一定程度的影响,这些因素共同构成了变电站场景中辅助通信的散射体来源。信号的传播会受这些散射体的反射、折射、散射作用,产生丰富的多径信号,故接收端接收的信号是来自直射路径和多种散射路径的合成信号。为了减少模型复杂度,且由于信号经过多次反射后,功率大幅衰减,终端接收到的信号微弱可忽略,故本文中的多径分量散射径仅考虑单次反射和双次反射。

图1 变电站室外场景Fig.1 Substation outdoor scene

将变电站室外无线通信场景等效为如图2所示3D圆形栅柱随机几何模型。模型中将圆柱均匀分成K个(图2设定为6个)等间隔排布高为H的区域,每个区域占据圆周1/12的范围,从离圆点最近的一个圆柱区域进行顺时针编号,如k1、k2、…、kn(n≤K)。圆柱截面圆的半径为R,圆心位于x轴

pn、ln分别为TX和RX的第n个天线单元;θkn为第kn个圆柱区域中心与圆心的水平方位角;θTR为TX到RX路径的水平方位角;为TX到RX路径的仰角;分别为散射体Sn与TX和RX的仰角;分别为散射体Sn与TX和RX的水平方位角图2 3D圆形栅柱GBSM模型Fig.2 3D circular grid column GBSM model

上,圆柱与x轴交点与o点水平最小距离为D,变电站室外散射环境包括变压器、塔杆、建筑物等散射体随机分布在这些栅柱面上,Sn是圆柱区域上的第n个散射体(n=1,2,…,N)。在本文研究中,设TX为静止发射端,RX为移动接收端,静止发射端TX位于z轴,高度为HT,由于其高度很高,故假设其周围没有散射体分布;移动接收端RX从原点o起始在x轴上向x轴正方向以v做匀速运动,高度为HR(HR≪HT)通常可以忽略。TX与RX上均采用均匀线性天线阵列,天线数量分别为p和l,考虑到计算复杂度,本文研究假设p=l=2。

变电站室外场景复杂,大规模电气设备对信号遮挡情况严重,某些区域设备排布密集,信号穿透性弱,且与信号发射端距离较远,由此可能出现没有LOS信号路径的情况。针对这个问题,在原模型的基础上,对模型进行LOS路径和NLOS路径分区,其中NLOS路径包括单反射(single-bounced,SB)分量和双反射(double-bounced,DB)分量,如图3所示。整个3D圆形栅柱随机几何模型划分为两个相等的区域,设置靠近TX的为含有LOS成分的LOS子区,远离TX的为无LOS成分的NLOS子区。

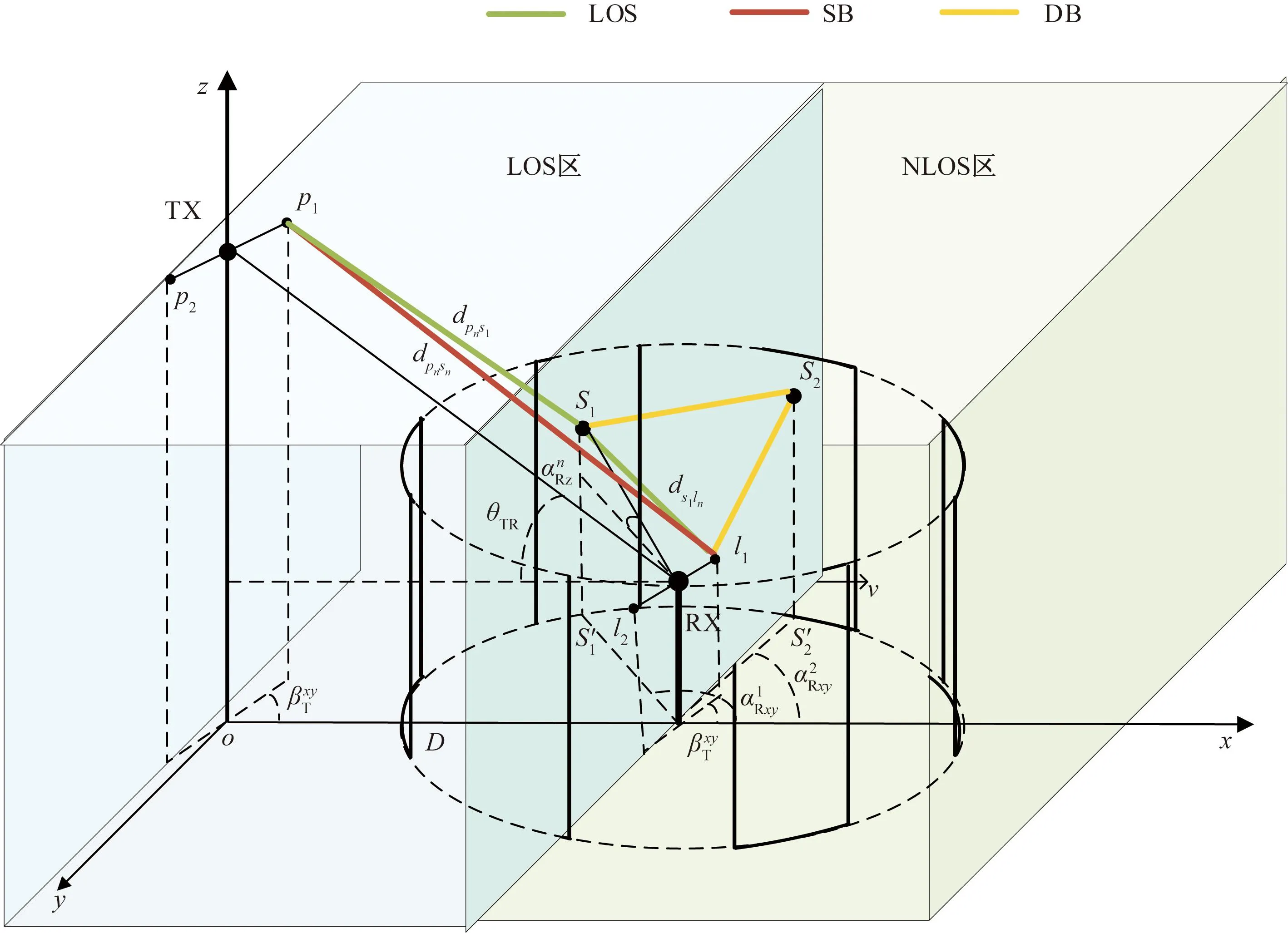
dpnSn为发射天线与接受天线间的路径长度;dpnS1为TX天线与散射体S1之间的距离;dS1ln为散射体S1与RX天线之间的距离图3 模型LOS子区与NLOS子区Fig.3 Model LOS subregion and NLOS subregion

由此,变电站室外固定发射端和移动接收端的信道复增益可分成以下两种情况。

1.1 LOS子区

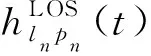
(1)

1.2 NLOS子区

(2)

式(2)中:

(3)

(4)

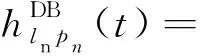
(5)

式中:dlnpn为第n个发射天线与第n个接收天线间的路径长度;dpnS1为第n个发射天线与散射体S1之间的距离;dS1ln为散射体S1与第n个接收天线之间的距离;dS1S2为散射体S1与S2之间的距离;λ为波长;K为莱斯因子;Ωlnpn为信道pn-ln的总功率;ηSB、ηDB分别为单次反射、双次反射路径的功率在散射总功率中的占比。

考虑到模型的复杂度,忽略高次反射的影响,假设ηSB+ηDB=1。φSB、φDB假设为区间[-π,π]上均匀分布的相位独立随机变量,N1、N2为散射点的数目,通常趋于无穷。fLOS、fSB、fDB分别为因接收端移动产生的直射径、单次反射径及双次反射径上的多普勒频移,通过将接收端速度向量分解为LOS路径、SB路径、DB路径上的速度,再结合模型中的几何关系,可得到其具体表达式为

(6)

式(6)中:θTR为TX到RX路径的水平方位角。

(7)

因此,

(8)

(9)

(10)

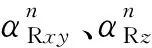
同时,截面圆的方程为

(11)

假设散射点Sn的坐标为(xn,yn,zn),根据空间几何定理和近似算法,即

(12)

p1、p2、l1、l2的坐标可通过收发天线的水平偏角、仰角和天线间距求出。通过空间两点距离公式推导得到直射路径、单次反射路径和双次反射路径即dp1l1、dp2l2、dSnl1、dSnl2的数学表达式为

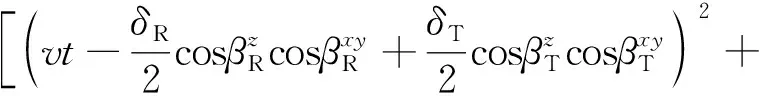
(13)

(14)

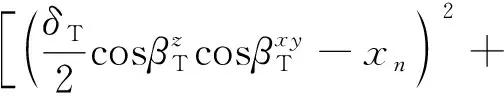
(15)

(16)

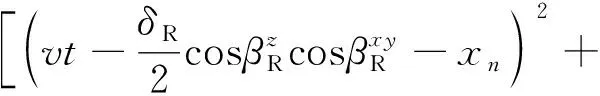
(17)

(18)

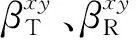
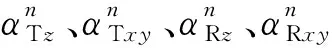
(19)

散射体的分布密度由非负实数kR(kR≥0)决定,kR值越大,散射体越集中分布在角度平均值附近,当kR=0时则视为各向同性环境。

2 参考模型的统计特性

2.1 空间-时间相关函数

空间-时间相关函数中引入天线间隔和时间变量为函数因变量,通过对不同天线单元的信道增益进行期望运算。ST-CT从空间及时间上反映了变电站室外圆形栅柱随机几何信道模型中任意两个天线单元子信道之间的相关性,其表达式为

(20)

式(20)中:E[·]为期望运算;*为复共轭运算;|·|为求模运算;τ为时间间隔。

本文模型的ST-CT函数Rp1l1,p2l2(t,δ,τ)由各自独立的LOS路径的ST-CT函数和散射路径的ST-CT函数复和组成,即

(21)

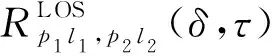
(22)

(23)

(24)

式中:dp1S1为第一个发射天线散射体S1之间的距离;dS1l1为散射体S1与第一个接收天线之间的距离;dp2S1为第二个发射天线散射体S1之间的距离;dS1l2为散射体S1与第二个接收天线之间的距离;dp2S2为第二个发射天线散射体S2之间的距离;dp1S2为第一个发射天线散射体S2之间的距离。

2.2 时间自相关函数

时间自相关函数(auto correlation function,ACF)从时间的角度反映了变电站室外无线信道因多径效应造成的影响,描述了通过不同路径到达接收端的信号之间的相关性,在多径环境恶劣复杂的变电站场景,此函数在很大程度上反映了信道的性能。令上文ST-CT函数中的δ=δT=δR=0,即可得到ACF函数的表达式为

(25)

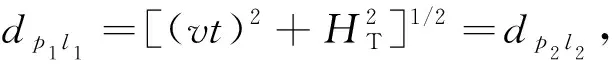
(26)

同理可得散射路径(SB/DB)的ACF公式:

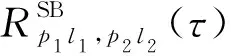
(27)

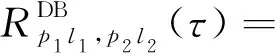
(28)

2.3 空间互相关函数

空间互相关函数(cross correlation function,CCF)从空间的角度研究不同MIMO天线单元间的相关性对信道性能的影响。当天线间隔过小时,会使天线单元之间产生很大的空间相关性,从而造成信道衰落,影响信道容量和误码性能。故反映空间相关性的CCF函数也是本文探究变电站室外无线信道性能的关键。令ST-CT函数中的τ=0,即可得到CCF函数的表达式为

(29)

LOS路径的CCF公式为

(30)

单次反射路径(SB)的CCF为

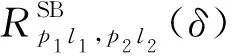
(31)

双次反射路径(DB)的CCF为

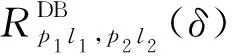
(32)

2.4 多普勒功率谱密度

变电站内移动接收端RX的运动会引起多普勒频偏,信道特性将受到影响,这种影响可从频谱角度,通过多普勒功率谱密度(doppler power spectrum density,DPSD)反映出来。DPSD可通过时间相关函数ACF的傅里叶变换求得,具体表达式为

(33)

式(33)中:S(fD)为DPSD;Rp1l1,p2l2(τ)为ACF的表达式;fD为系统的多普勒频移,但因为LOS、SB、DB路径的多普勒频移不同,故需要先根据3种路径的ACF和多普勒频率分别求出LOS、SB、DB路径的SLOS(fLOS)、SSB(fSB)、SDB(fDB),再复合相加得到S(fD),具体表达式为

(34)

(35)

(36)

S(fD)=SLOS(fLOS)+SSB(fSB)+SDB(fDB)

(37)

3 仿真模型

参考模型的ST-CF、ACF、CCF函数是基于设定变电站散射点个数趋于无穷且服从VMF分布推导而出的,其中无线信号传播路径的AOA和AOD都是非确定且连续的,故接下来可通过设置有限离散散射点个数,求出每个散射点的AOA和AOD,则可得到该变电站随机几何模型的仿真模型。仿真模型的ST-CF表达式为

(38)

其中LOS路径的ST-CF为

(39)

SB路径的ST-CF为

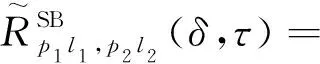
(40)

DB路径ST-CF为

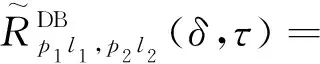
(41)

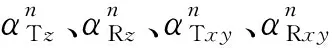
(42)

(43)

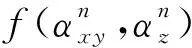
4 仿真结果

通过分析变电站随机几何模型的散射路径几何关系进行数学推导得到了变电站无线信道参考模型和仿真模型的ST-CT、ACF、CCF、DPSD的表达式,但仅凭借数学公式很难直观地看出这些自相关函数随时间或空间的变化趋势和其中的关键参数如莱斯因子K、VMF分布中kR等对模型性能的影响。同时,也无法对比分析上文中LOS和NLOS子区在信道自相关特性上的差异,所以本文研究中使用MATLAB对所得出数学模型进行仿真。

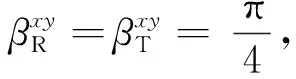
图4、图6、图7和图9分别是两组参考模型与仿真模型在LOS子区和NLOS子区的时间自相关函数ACF对比图和空间自相关CCF曲线对比图,从图4、图6、图7和图9中可看出,两个模型的ACF曲线和CCF曲线虽略有波动,但整体上两根折线呈现较为贴合的现象。由此可验证本文参考模型的正确性和仿真模型的可行性。

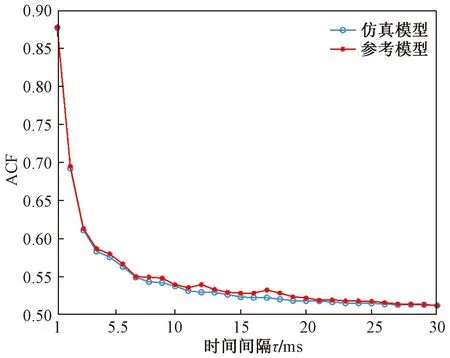
图4 LOS子区时间自相关ACF Fig.4 LOS subregion time autocorrelation ACF

图4中,在τ<5的区间内,LOS子区的ACF的值都大于0.55,并且呈现一个急剧下降的趋势。这说明在时间间隔比较短的时候,信道的时间自相关性比较大,时间间隔的变化会对ACF的值造成巨大影响;但在5之后,ACF下降趋势明显变缓,并趋近一个接近于0的值,说明该模型的时间自相关性随着时间间隔τ的增大而变小,且无限趋近一个很小固定值。

图5是模型的CCF随TX和RX天线间隔变化趋势三维图,从图5中可以明显看到在TX、RX天线间距较小时,对信道空间自相关性的影响是非常明显的。图6的二维图更加明显地看出在RX天线(间距TX天线同理)从1到3有一个陡峭的下降坡度,而随着天线间距的逐渐加大,CCF的值也逐渐稳定在一个接近于零的值。在三维图中还可以看出,在天线间距在2.5～3.5,CCF曲线还出现了轻微的振荡和起伏。这个现象产生的原因主要是两点:其一,LOS分量的存在会对CCF造成影响,使其发生波动;其二,非同向异性的散射体分布也会使CCF波形不稳定,但整体还是趋近于平稳的。

图5 LOS子区空间自相关CCF三维图Fig.5 Three-dimensional CCF of spatial autocorrelation in LOS subregion

图6 LOS子区CCF随TX天线间隔的变化趋势图Fig.6 Trend diagram of CCF in LOS subregion with TX antenna interval

为了验证LOS成分对变电站随机几何模型性能造成的影响,剥去路径增益中LOS路径分量,得到NLOS区域的ST-CT、ACF、CCF公式,并对其在MATLAB里仿真,研究对比LOS区域和NLOS区域的性能优劣性。图7是NLOS区域的时间相关函数ACF曲线,从图7可以看出,随着时间间隔的增加,NLOS区域的ACF值也是在时间间隔较小时急剧下降,而后逐渐趋于平缓并保持稳定。将其与图3进行对比,虽然二者图形趋势相似,但从图3可以读出,LOS区域ACF的起始值是0.87,最终值是0.5,而NLOS区域ACF的起始值是0.39,最终值仅为0.01了,这说明在时间间隔非常大的情况下,NLOS区域的时间相关性是小于LOS区域,也就是说,LOS成分会导致无线信道时间相关性的增大。

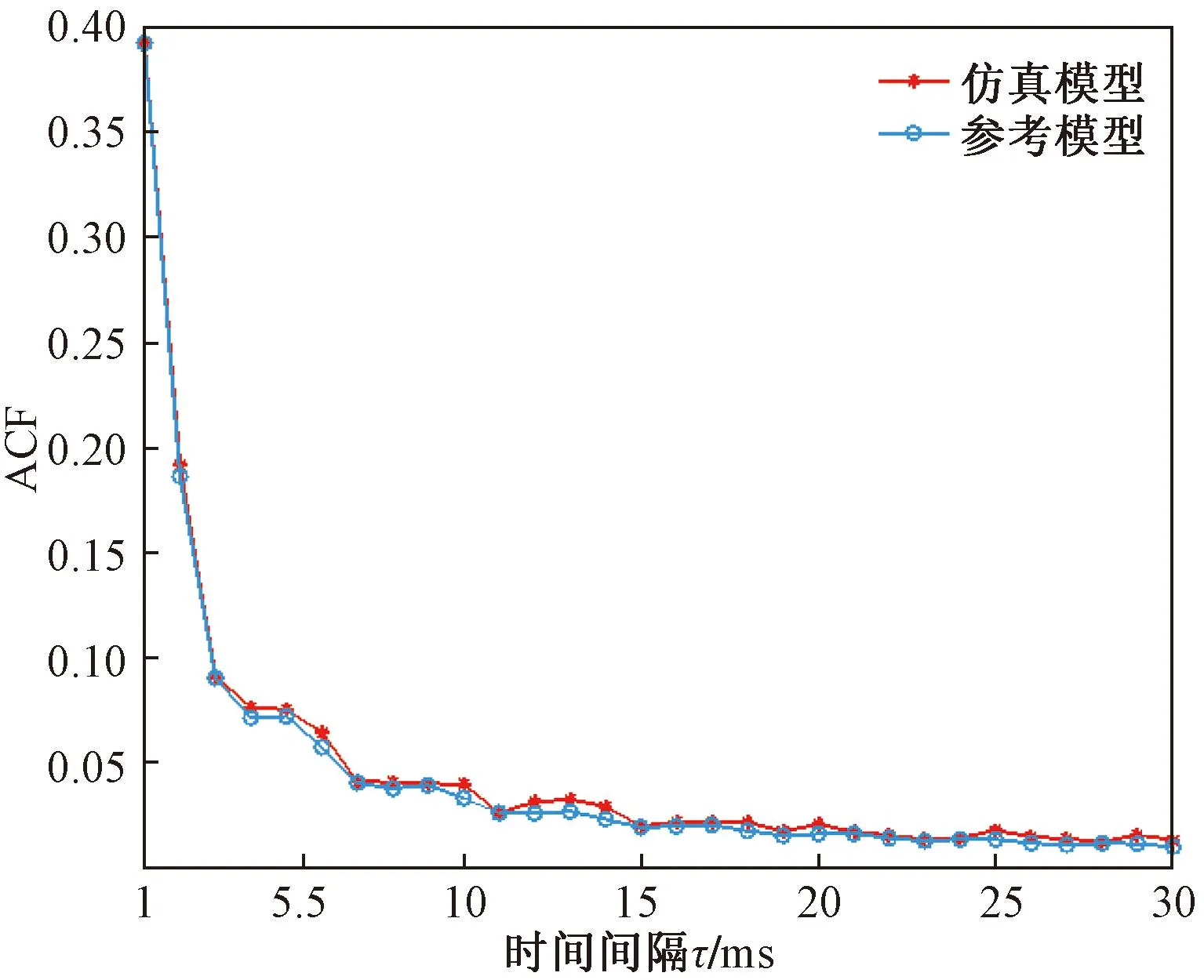
图7 NLOS子区时间相关函数ACFFig.7 NLOS subregion time correlation function ACF

同理,将图8的NLOS区域时间相关函数CCF与图5进行对比,NLOS区域的CCF曲面图整体走向与也LOS区域大致相同,都是CCF的值在天线间隔较小时快速下降,然后随着TX和RX天线的间隔增大,下降的趋势变得平缓。但相比与LOS区域,当天线间隔变得较大时,NLOS区域的CCF曲线振荡的幅度/更小,这一点可证明上文中LOS成分对空间相关性的影响。同时,图6和图9中更加明显的是图像起始点和终点大小的区别:图6中,LOS区域CCF图像的起始点/终点是0.85/0.5;图9中,NLOS区域起始点/终点是0.35/0.006。二者对比可得出,随着天线间隔的不断增大,NLOS区域的空间自相关小于LOS区域,天线间隔的对信道性能的影响在LOS区域是不会因为其间隔增大而消失的。

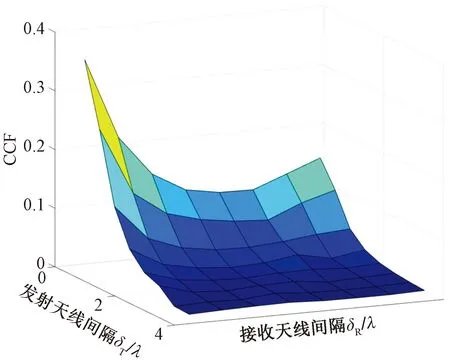
图8 NLOS子区空间自相关CCF三维图Fig.8 Three-dimensional CCF of spatial autocorrelation in NLOS subregion

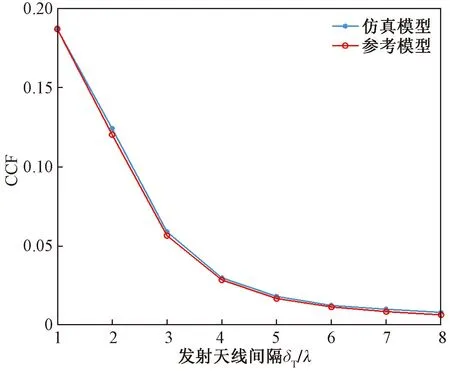
图9 NLOS子区CCF随TX天线间隔的变化趋势图Fig.9 Trend diagram of NLOS subregion CCF with TX antenna interval

图10通过对比LOS区域和NLOS区域的ACF和CCF曲线,证明了LOS成分对变电站随机几何模型性能是有不可忽视的影响的,但不能看出其两者之间的具体关系。由于当接收信号有LOS成分时,信道是服从莱斯分布的,莱斯因子K的定义是LOS路径信号与多径信号方差之比,即表示LOS在信号中的占比,K越大,LOS占比越大。所以本仿真通过变化K值,研究LOS成分对信道自相关性的影响。图10对LOS区域在K=1、K=3、K=5、K=10的时间相关性和空间相关性进行了仿真。从图10中可以读出,莱斯因子越大,ACF和CCF曲线越高,从而能够得出LOS成分越多,信道的自相关性越大的结论。但随着K不断增大,曲线之间的间隔有所缩小,这说明这种影响并不是无限的。

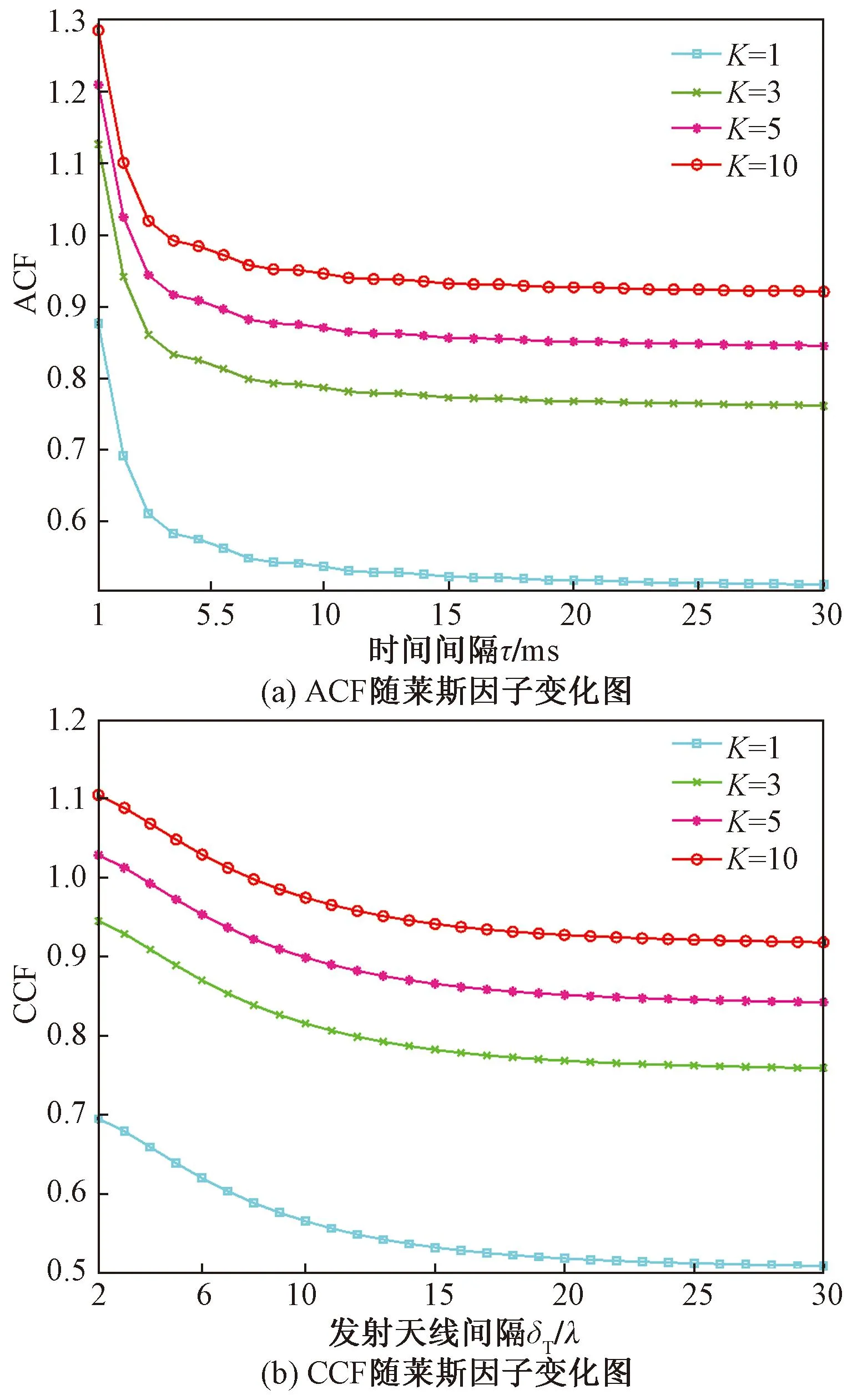
图10 LOS子区ACF、CCF随莱斯因子变化图Fig.10 Plot of LOS subregion ACFand CCF as a function of Rice factor

图11和图12分别为对应不同kR的情况下,ACF和CCF曲线的变化图。因为在VMF分布中,参数kR的大小影响着散射体的分布,kR越大,代表散射体分布越靠近均值角附近,且当kR=0时为各向同性分布。所以可以看出,ACF和CCF曲线都有随着kR的增大而上升,但因为kR主要控制的是空间分布,故这种影响对时间自相关性是不明显的,图11中4根曲线间隔很小,在kR较大时,ACF曲线甚至基本重合。然而在空间自相关CCF图中,随着kR的变大,CCF曲线的升高就很明显了,这验证了散射体分布越靠近均值角度,空间自相关性约显著。同时从kR=0到kR≠0曲线快速升高的走势还可说明,非各向同性环境空间自相关性大于各向同性环境。

图11 ACF曲线随kR变化图Fig.11 ACF curve as a function of kRvalue

图13是多普勒功率谱密度在不同RX速度下的随时间变化图。从图13中可以看到,当RX速度v=1时,多普勒功率谱最集中,数值最大,速度逐渐增大到v=5时,能量相对集中但明显降低,到v=10时,功率谱分散成了两簇,能量不再集中在一处,这说明到RX运动速度增大,会导致多普勒功率谱密度分散并降低,验证了移动端的速度大小会影响信道性能。

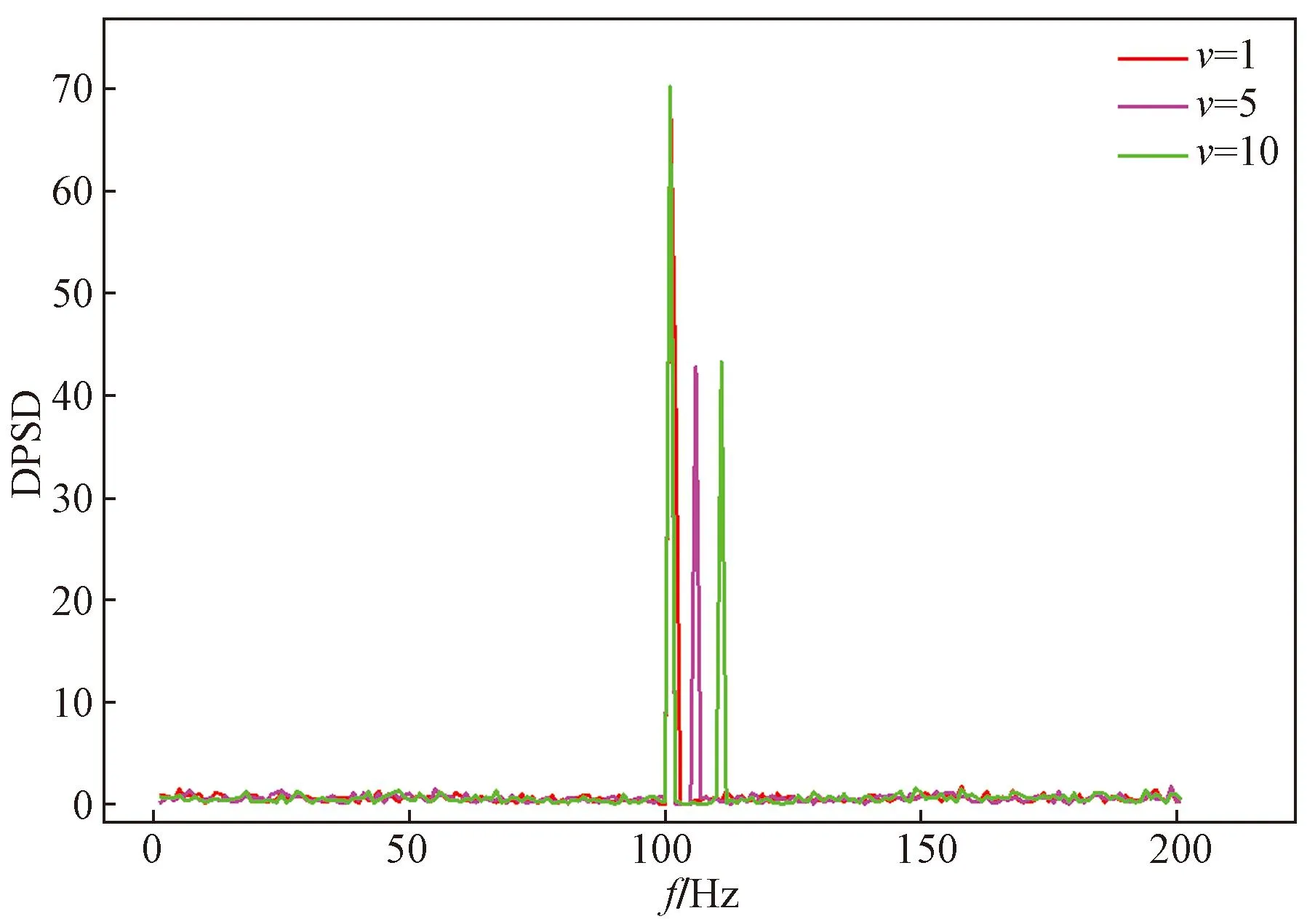
图13 DPSD随速度变化图Fig.13 Diagram of DPSD as a function of velocity

5 结论

针对变电站室外存在大型设备遮挡、设备种类多样且分布密集的特点,提出了圆形栅柱的随机几何模型,考虑到圆栅柱比封闭圆柱具有更多的LOS分量,又将模型进行了LOS和NLOS,并在栅柱上用VMF分布,栅柱间认为概率密度为0;同时模型内设置固定发送端和移动接收端来讨论变电站实际应用的辅助通信场景,使模型具有非平稳性。考虑到算法复杂度,在模型中仅仅考虑LOS、SB和DB3种路径,通过几何分析,推导出3种路径的SF-CF、CCF、ACF函数并用MATLAB仿真,从仿真图中可以验证本模型的正确性;通过改变参数到K、kR的值,比较分析出LOS分量和散射体分布对信道性能有较大的影响,还仿真了在不同终端速度下的PSD,仿真结果也证明了多普勒效应对信道性能有不可忽视的影响。本文研究运用随机几何模型对变电站室外通信场景进行建模,分析了此场景下的信道性能,为变电站内的通信工作提供了理论指导,也为未来针对变电站进行信道建模提供了思路。