船用汽轮机变工况的遗传粒子群优化智能控制方法研究
2024-01-12张磊李源林安袁陈臣
张磊, 李源, 林安, 袁陈臣
(1.海军工程大学动力工程学院, 武汉 430033; 2.武警海警总队第五支队, 三亚 572032)
汽轮机组是船舶动力装置中核心能量转换设备,将蒸汽发生器产生的蒸汽热能转换为电能或机械能,为船舶提供全船电力和主动力[1]。为了满足船舶航速的需要,汽轮机需要变工况运行,且工况变化频繁,其控制精度和控制性能要求非常高。汽轮机数字电液(digital electric hydraulic,DEH)控制因其具有控制原理简单、算法适合工程应用等优点,已成为汽轮机重要的控制方式[2-3]。然而常规比例、积分、微分(proportion integration derivative, PID)由于参数整定依靠经验公式,不仅计算量大、耗时较长,而且难以获得性能最优的参数。借助遗传算法[4]、粒子群算法(particle swarm optimization,PSO)[5]、人群搜索[6]等人工智能算法优异的全局搜索能力改进PID控制,在搜索范围内快速寻找到最优参数,具有运算效率高、通用性强等优点。但由于船用汽轮机组运行时具有很强的不确定性、非线性、耦合性等特点,应用常规智能算法难以得到较好的控制效果。因此,发展具有强大全局搜索能力,且具有较高搜索速度和精度的汽轮机变工况自适应智能PID控制方法[7-8],能够减少负荷扰动和参数变化对机组动态特性的影响,并实现船用汽轮机组变工况智能优化控制及安全稳定运行。模糊控制[9-10]不依赖于被控对象的数学模型,凭借专家知识和操作者的控制经验,能够实现对复杂系统的良好控制,且控制效果基本不受干扰和参数变化的影响,应用于非线性、时变性系统中具有较大优势。但是其量化因子和比例因子凭借专家知识和人工经验取值,具有很强的局限性,难以获得比较理想的控制效果。粒子群算法因其具有收敛快、参数设置少、易实现等优点,在模糊PID的参数优化中应用广泛[11-12],PSO虽然能够有效改善模糊PID的控制性能,但其优化过程容易出现“早熟”现象,导致参数优化精度不足。
为此,现提出一种船用汽轮机变工况的遗传粒子群优化智能控制方法,以汽轮机组调节系统各部件的模块化数学模型为基础,建立汽轮机组数字电液(digital electric hydraulic ,DEH)闭环模糊PID控制模型,提出融合遗传算法的粒子群优化算法,构建汽轮机变工况自适应智能控制模型,实现船用汽轮机组大幅度变工况智能控制优化及动态响应分析。
1 汽轮机组DEH闭环的模糊PID控制模型
船用汽轮机组调节系统主要由PID控制器、电液转换器、油动机、汽轮机、发电机和反馈机构等构件组成,实现汽轮发电机组的转速调节等功能。本文研究建立了船用汽轮机组控制部件的传递函数模型,将控制输入信号依次经过模糊PID控制器和部件传递函数模块产生输出信号,输出信号至电液执行器,并将输出信号作为负反馈信号,建立一个汽轮机组DEH闭环模糊PID控制系统结构,如图1所示,其中PID控制信号为

Integrator为积分;Mux为两输入;Demux为三输出;Product为乘积符号;du/dt为u的微分;Te、Tu、Tv、Ta为各调节组件的时间常数图1 汽轮发机DEH闭环的模糊PID控制模型Fig.1 Fuzzy PID control model of DEH closed-loop steam turbine generator
(1)
式(1)中:e(t)为给定转速信号n(t)和反馈信号ny(t)的偏差;Kp、Ki、Kd分别为对误差信号e(t)及其积分、微分量的加权。
图1所示模糊PID控制基本思路为:控制器的输入变量为e(t)和de(t)/dt,并通过量化因子Ke、Kec对偏差信号e(t)和偏差信号的变化率de(t)/dt进行模糊化处理;经过模糊推理后得到输出变量为模糊量ΔKp、ΔKi、ΔKd,通过采用比例因子K1、K2、K3对Kp、Ki、Kd进行解模糊处理,计算出控制参数的修正量K′p、K′i、K′d;得到控制参数的修正方程:Kp=Kp0+K′p;Ki=Ki0+K′i;Kd=Kd0+K′d,式中,Kp0、Ki0、Kd0为汽轮机组DEH闭环的模糊PID控制器的初始参数。确定上述变量的论域,将Ke和Kec的论域取为[-5,5]和[-3,3],ΔKp、ΔKi、ΔKd的论域为[-3,3]、[-0.06,0.06]和[-1,1];并选择变量Ke的NB为高斯型隶属度函数,变量ΔKp、ΔKi、ΔKd的NB和PB为梯形隶属度函数,其余均为三角型隶属度函数,其中模糊集为{NB,NM,NS,ZE,PS,PM,PB},对应真实语言变量为{负大,负中,负小,零,正小,正中,正大}。根据PID参数调整随Ke、Kec变化规律,为ΔKp、ΔKi、ΔKd各制定49模糊规则,典型规则如表1所示。
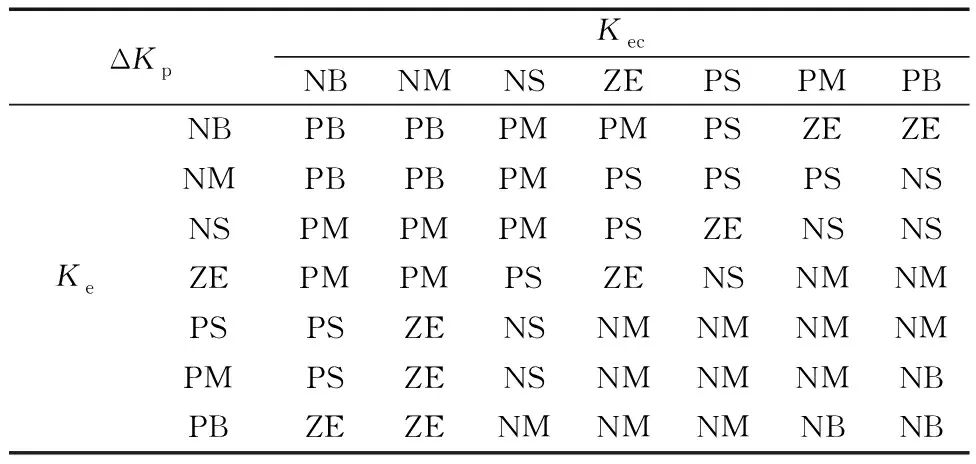
表1 ΔKp规则Table 1 ΔKp’s rule
输入变量经过模糊化和模糊推理后,输出的是3个模糊量,需要将它们转化成清晰的数值,这个转化的过程称为解模糊。解模糊的方法有很多,本文研究选择面积重心法,通过比例因子的解模糊作用得到模糊PID参数的真实变化量。
2 基于遗传粒子群算法的智能模糊PID参数优化
2.1 遗传粒子群算法及实施流程
本节将提出融合遗传算法的粒子群优化算法,实现闭环汽轮机模糊控制参数智能优化,其具体优化流程如图2所示,其基本步骤如下。

图2 模糊控制智能优化算法流程图Fig.2 Flow chart of fuzzy control intelligent optimization algorithm
步骤1初始化种群,确定种群规模N,最大进化代数Tmax,最大与最小惯性权重为ωmax、ωmin,最大与最小速度为Vmax、Vmin,交叉概率Pc,变异概率Pm,学习因子c1、c2;根据模糊PID控制器的量化因子Ke、Kec与比例因子K1、K2、K3的参数变化范围,产生一个初始粒子群,每个粒子对应一组参数值,根据速度范围随机生成初始种群的速度矩阵,具体参数设置N=30,Tmax=30,ωmax=0.9,ωmin=0.1,c1=1.3,c2=1.7,速度范围为[-1,1]。
步骤2适应度评价,通过运行汽轮机模糊PID控制的传递函数仿真模型,得到每组量化因子与比例因子参数对应的性能指标,传递给粒子群的优化算法作为粒子的适应度;根据适应度值记录初始种群个体最优与全局最优,其中初始个体最优为粒子自身,将适应度值最小的初始个体最优视为全局最优,适应度计算公式为
(1)
步骤3更新粒子的速度与位置,为了减小算法陷入局部最优值的概率,在学习因子c1和c2的表达式前加入一个自适应变异随机数进行修正,粒子的位置X与速度V更新公式为
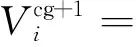
(2)
(3)
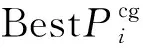
(4)
步骤4融合遗传算法的选择、交叉、变异等遗传操作,根据适应度大小对粒子进行排序,选择种群中M(大于N/2的偶数)个亲和度最高(适应度最低)的粒子;然后依照交叉概率Pc对选中的粒子执行随机交叉操作,产生M个子代粒子,并将父代粒子进行替换,子代粒子位置与速度公式为
zx=rand×mx1+(1-rand)mx2
(5)
(6)
式中:mxi、mvi为第i个父代粒子的位置和速度;zx、zv为子代粒子的位置和速度。
变异操作:用交叉完的M个粒子替换交叉前种群中M个亲和度最低的粒子,得到新的种群N′,按照变异概率Pm对全部个体执行变异操作,假如适应度函数值fitness(mx+b) 步骤5计算执行遗传操作后种群中粒子的适应度,更新个体最优与全局最优,当算法满足终止条件时(达到最大进化代数或最小适应度值),则算法结束运算,输出最优量化因子与比例因子;否则转至步骤3重新计算,直至算法满足终止条件。 将得到的最优量化因子和比例因子代入汽轮机组DEH闭环的模糊PID控制传递函数模型,该模型可以实现任意一个任务剖面的汽轮机组变工况自适应控制及动态特性分析。 本节将选取Rastrigin和Sphere两个标准测试函数从收敛速度和收敛精度两个方面来分析遗传粒子群优化算法的性能。通过遗传粒子群优化算法计算,得到基础PSO改进前后的Rastrigin函数和Sphere函数适应度进化曲线如图3所示,在两种标准测试函数下,遗传粒子群优化算法的适应度进化曲线总能在更少的迭代次数下达到最低适应度处,能够说明遗传粒子群优化算法相比于基础PSO具有更快的收敛速度。 图3 适应度进化曲线Fig.3 Fitness evolution curve 计算20次Rastrigin函数和Sphere 函数下基础PSO算法和改进的遗传PSO算法(IPSO算法)的适应度均值以及运行时间均值如表2所示。 表2 适应度与迭代时间对比Table 2 Fitness versus iteration time 由表2可得,在两个标准测试函数下,IPSO运行20次的平均适应度不仅比基础PSO的平均适应度小很多个数量级,而且完成相同迭代次数所需要的时间更短,充分说明IPSO相比于基础PSO具有更快的收敛性能。 以某船用汽轮机组大幅变工况为例:机组保持额定工况运行(额定转速为3 000 r/min),运行一段时间后甩到某一低速稳定运行工况,持续运行一段时间后,再加速至额定负荷。该汽轮机组传递函数时间常数取为Te=0.01、Tu=0.2、Tv=0.25、Ta=8,数值计算中的仿真步长为0.01 s,仿真时间为500 s,得到不断寻优后量化因子和比例因子的值为:Ke=5.569 1,Kec=1.896 4,K1=5.541 2,K2=8.880 6,K3=4.600 1。 将基于遗传粒子群优化算法的智能模糊PID控制方法(IPSO-模糊PID法)、PID、模糊PID分别应用于某船用汽轮发电机组极端工况控制验证。当汽轮机运行10 s后,在0.5 s时间内甩100%阶跃负荷,计算得到3种控制方法汽轮发电机转速响应曲线如图4所示:甩负荷时,传统PID控制算法计算超过额定转速140 r/min;模糊PID算法超过额定转速约100 r/min;IPSO-模糊PID算法超过额定转速约75 r/min,且在5 s左右时间就已经恢复至额定转速。可见本文建立的IPSO-模糊PID算法在汽轮机甩负荷工况运行时具有更小的动态超调量和更短的调节时间,表现出了更好的控制性能,能够有效改善汽轮机突卸负荷工况的转速控制性能。 图4 汽轮发电机甩负荷转速响应曲线Fig.4 Speed response curve of turbine generator load shedding 为分析基于IPSO优化的智能模糊PID的稳定性能,采用上述3种PID研究汽发机组阶段甩负荷对转速响应的影响。典型任务剖面负荷变化曲线如图5所示,0代表额定负荷,-1代表甩100%阶跃负荷,仿真步长为0.01 s,仿真时间为100 s,得到汽发机组的转速随负荷变化的响应曲线如图6所示。 图6 变负荷时的转速变化曲线Fig.6 Speed response curve of turbine generator variable load 由图5和图6可得,随着机组甩负荷的变化,机组的转速随之快速改变,本文的IPSO-模糊PID智能自整定方法在变工况过程中的转速波动值约为1%,其调节精度明显高于PID控制算法的3%。IPSO-模糊PID算法在汽轮机变工况控制过程中表现出的震荡幅度和调节速度始终优于模糊PID和常规PID,其只自适应调节能力和稳定性更佳。 转子时间常数Ta的变化对机组动态特性的影响较Te、Ts和THP更显著,且船用汽发机组经常处于变工况运行,建立传递函数时不能将Ta作为恒定值。因此,采用上述3种PID研究Ta的变化对机组转速输出的影响。Ta的变化曲线如图7所示,负荷变化曲线如图8所示,仿真步长为0.01 s,仿真时间为250 s,得到汽发机组甩负荷随参数Ta变化的转速响应曲线如图9所示。 图7 参数Ta随时间变化曲线Fig.7 Curve of parameter Ta over time 图8 负荷随时间变化曲线Fig.8 Curve of load over time 图9 连续突变负荷时的转速变化曲线Fig.9 Speed response curve of continuous mutational load 采用上述3种PID控制器研究参数Ta的变化对汽轮机连续变工况转速响应的影响,如图9为汽轮机变工况时参数Ta随转速变化曲线,可见3种PID控制下汽轮机变工况的动态超调量和转速稳定时间均会发生变化。在外界负荷突变、Ta时间常数大幅度变化的情况下,基于IPSO-模糊PID法控制下转速的动态超调基本维持在2%~3%,明显优于其余两种算法的3%~5%,且其超调量随Ta改变的变化幅度和调节至稳定的时间始终小于模糊PID和传统PID控制算法,进一步验证本文提出的智能控制方法具有更好的控制稳定性和鲁棒性。 (1)汽轮机组DEH闭环的模糊PID控制模型能够综合考虑机组的死区、摩擦等非线性因素,且能够准确反映机组大幅变工况时转速超调量过大、调节时间过长、鲁棒性不足的实际运行特性。 (2)在PSO算法中引入随迭代次数自适应变化的幂和融合类似遗传算法的选择、交叉、变异等遗传操作,能够有效改善基础PSO易陷入局部最优的缺陷,通过测试函数验证了IPSO优化算法具有更好的计算效率和收敛精度。 (3)基于遗传粒子群智能优化算法的汽轮机变工况自适应智能模糊PID控制模型能够实现模糊PID的量化因子Ke、Kec与比例因子K1、K2、K3最优化设计,进而实现了船用汽轮机组大幅度变工况智能控制优化,且该智能控制方法能够弱化负荷频繁变化和参数扰动对机组动态特性的影响,具有优越的自适应控制性能。2.2 遗传粒子群算法性能分析

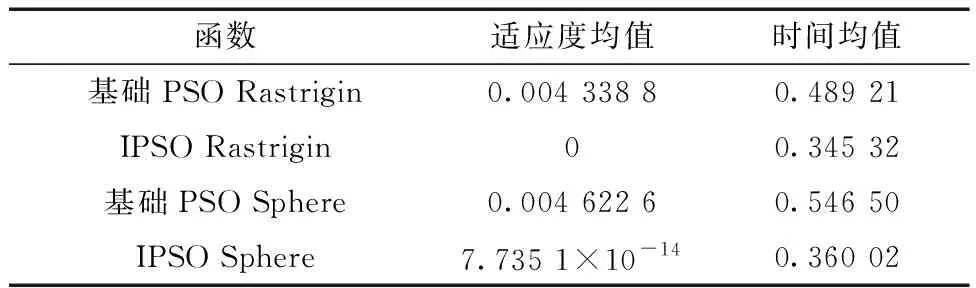
3 船用汽轮机组大幅变工况动态特性分析
3.1 汽轮发电机组突卸负荷工况分析

3.2 汽轮发电机组连续甩负荷动态分析
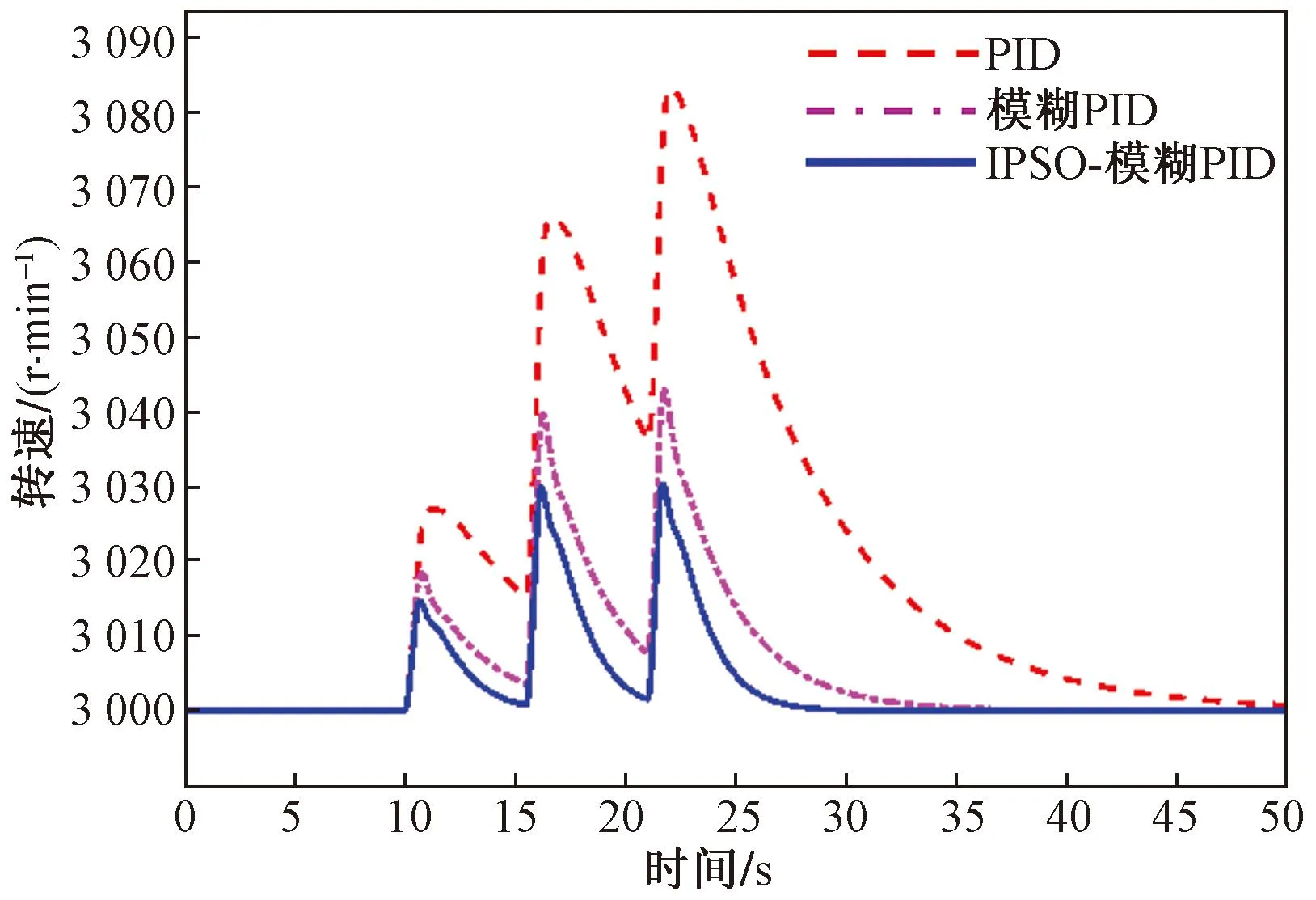
3.3 参数扰动的鲁棒性分析

4 结论
