基于高斯混合模型的粒度数据分析新方法及沉积相应用

雷晓虹, 尹太举*, 赵红静, 王杨君, 李昂达, 李佳洋, 石放, 侯新宇

(1.长江大学地球科学学院, 武汉 430100; 2.长江大学资源与环境学院, 武汉 430100;3.塔里木油田勘探开发研究院, 库尔勒 841000)

沉积物粒度是衡量沉积介质能量和沉积环境能量的重要指标[1]。而粒度的垂向变化,可以反映地质历史时期沉积营力的演化特征[2]。

由于母岩风化后的产物在搬运和沉积过程中多个“动力组分”叠置[3],造成某些粒级物质优先富集[4],属于连续有序的随机过程的动力学总体,故沉积物粒度分布为一个复杂的多变量函数。 实验表明[5],自然界的粒度由2个及以上次总体混合分布且符合高斯分布[6],基本呈现为双峰或多峰(多众数)的驼峰状[7]。若想通过粒度反演沉积过程,对粒度分布的敏感组分进行分离和提取[8]才是有效的解决办法。

目前最常用的粒度分析图件为粒度概率累计曲线。Visher[9]用概率累计曲线图上的线段数解释搬运作用类型,但该方法存在以下问题,①根据统计学理论,当对数坐标系下的样本累积分布如果近似于n条直线,则不能说明该样本来自n个正态母体[10];②有很大的主观性无法分离、提取与沉积过程相关的粒度分布次总体[11]。

为解决当前图件存在的问题,本文引用高斯混合模型应用至粒度分析中,构建粒度次总体拟合图。目前,高斯混合模型已被应用至水文学[12]、地球化学[13]等领域,并逐渐演变为分析不同种类异质分布的工具[14]。而该模型尚未应用至粒度与沉积学关系的研究中。

以渤海湾盆地馆陶组为例,结合岩心剖面、沉积微相等资料,探寻无监督聚类的高斯混合模型能否精确识别各个粒度分布中的次总体、探寻参数的地质意义并验证方法的有效性和适用性。

1 研究区概况

研究区所在的渤海湾盆地断裂体系十分发育,伸展和走滑断裂系统上下叠置、交错,控制了盆地“东西分带、南北分块”的基本构造格局。其处于渤海最大的富生烃洼陷--渤中洼陷东南部渤南凸起高部位[15],经历了印支运动、燕山运动及喜马拉雅运动的演化和改造[16](图1)。

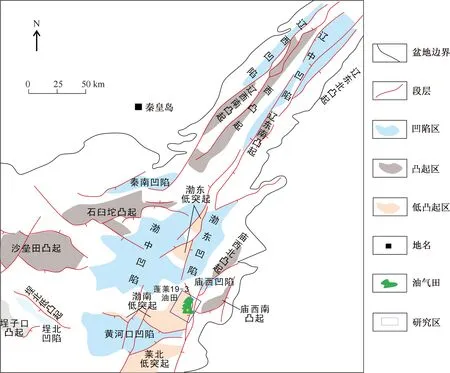
图1 PL19-3油田区域构造位置图Fig.1 Regional structural location map of PL19-3 oilfield

馆陶组沉积时期整体属于亚热带季风气候,温暖湿润[17]。早期主要受东部胶辽隆起控制,沉积类型为辫状河;馆陶组沉积中晚期至明下段时期主控物源转变为辽东隆起,沉积类型逐渐由近缘的辨状河沉积演变为远源曲流河沉积,属于辫状河与曲流河的过渡相类型[18]。馆陶组下部为厚层状灰色砂砾岩、含砾砂岩、砂岩夹紫红色、灰绿色和暗灰色泥岩[19],其中砂岩以细-中粒为主,单层厚度2～15 m,孔隙度20%～35%,粒度概率累积曲线为一段式,粒度中值4.0～700.0 μm(图2),分选中等到差[20];上部为灰色砂砾岩、砂岩与暗红色泥岩互层,其中粒度为粉-细粒,砂岩单层厚度1～5 m,孔隙度28%～35%,粒度概率累积曲线为两段式,粒度中值10.0～500.0 μm,如图2所示,分选中等到较差[20]。整体粒度成下部粗、上部细的特点,与下伏古近系不整合接触[19]。

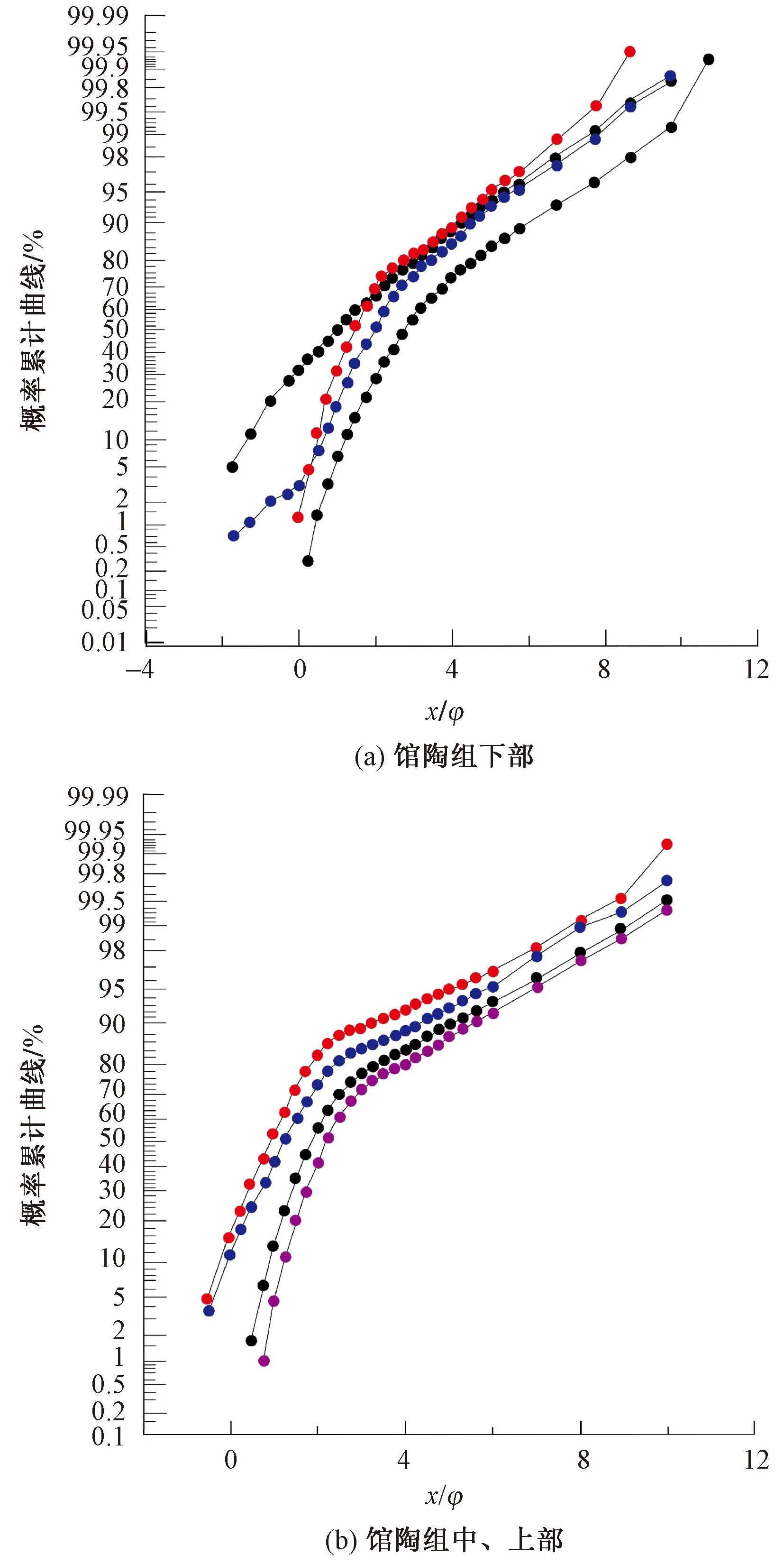
φ为粒径图2 PL19-3-8ST井馆陶组下、中上部粒度概率累计曲线Fig.2 Cumulative curve of grain size probability in the lower, middle and upper part of Guantao Formation in Well PL19-3-8ST

2 方法

2.1 高斯混合模型

高斯混合模型(Gaussian mixture model,GMM) 是将一个事物分解为若干个高斯概率密度函数加权和的模型[21-22],依据群集概率分配群集成员,构建多元高斯分布模型[23-24](图3),从而找寻合理的数据分布规律和划分方案。其数学表达式为

φ为粒径图3 GMM曲线及参数示意图Fig.3 Schematic of GMM curves and parameters

(1)

式(1)中:fk(xi|θk)为多元正态密度函数;xi为第k类的密度函数;θk为相应的参数。θk由均值μk和协方差矩阵σk组成,每个向量xi都是P维的矢量。所以该分布P由G个高斯密度函数加权平均后概率密度函数表达式为

(2)

式(2)中:wk为各分量的权重;G为成分数。

Dempster等[25]提出EM算法,可在给定粒度数据集合X的情况下,寻找合适的参数θ,使似然函数最大。研究区粒度数据集合X={x1,x2,…,xn},xi从集合X中抽取,集合中元素相互独立且符合高斯混合模型。

其中,最优聚类群集数k(即聚类簇数)是求解高斯混合模型拆分次总体数目的关键,k常被用作评价聚类结果的性能指标[26-28]。为选择最佳聚类群集数k,采用均方误差(mean squared error,MSE)[29-30]及确定系数(R2)2种误差评价标准,这些标准可定量识别最优聚类群集数k并权衡参数似然估计拟合度好坏。因此MSE越小,模型精确度越高,误差值越小,值为0即为完美的模型[31]。因R2取值范围在[0,1],取值越接近1表示模型逼近效果越好[32]。

2.2 粒度数据的升采样

为解决现有数据仅为激光粒度仪分析报告而导致数据量匮乏的问题,通过数据升采样模拟一组符合概率分布的粒度分布仿真数据集的方法,实现概率值到精确值的转换,其中升采样过程中产生的空值可以通过线性插值等方式进行填充[33]。

本文研究对每组原始数据进行升采样模拟,生成 2 000个且符合概率分布的仿真数据点,保证次总体拟合图误差足够小。

3 结果分析

3.1 处理数据

以渤海地区馆陶组P井1 250.4 m为例。

(1)将激光粒度仪分析报告整理为概率分布直方图,如图4(a)所示。

φ为粒径; λ为面积; μ为均值; σ为方差; M为峰值; C1、C2为次总体1、2; P1/2为交点; S1为重叠面积图4 1 250.4 m样本拟合过程和拟合结果Fig.4 Fitting process and fitting results of 1 250.4 m samples

(2)将原始样本升采样,模拟符合概率分布的粒度分布仿真数据集,如图4(b)所示。

(3)计算聚类数目从1～10时,MSE及R2数值大小并比较其大小。当k=2时, MSE最小,R2最大,即k=2为最佳聚类群集数。

(4)将k=2代入EM算法内,求解均值μi(μi为样本均值,表示一组样本密度概率最大时对应的粒径值,μi<0时,为砾岩;μi>0时,μi越大粒径越小)与方差σi(σi为样点标准差,表示随机变量取值的分散程度。σi值越小,峰值Mi越高;μi对应的密度概率值为峰值Mi,Mi是反映其尾数变化判断沉积环境的有用粒度参数[7])。计算得μ1=1.27,μ2=6.51,σ1=0.65,σ2=2.42。

(5)依据μi与σi,绘制次总体拟合图,如图4(c)所示,运用数形结合思想,获取交点及面积,如图4(d)所示。

(6)结合岩心剖面,判断分析沉积微相,探讨不同组分的沉积机理和指示意义。

3.2 沉积相识别

截取该研究区馆陶组PL19-3-8ST井典型深度段1 414～1 426 m、1 490～1 506 m并绘制岩性剖面和次总体拟合图(图5和图6),1 414～1 426 m下部棕黄色粒质砂岩、细砂岩,发育板状交错层理、槽状交错层理,氧化及强氧化环境。中部为灰黑色泥岩、灰褐色泥质粉砂岩,还原环境。上部棕黄色含砾砂岩、细砂岩,发育板状交错层理,局部可见灰黑色粉砂质泥岩,主要为氧化及强氧化环境。由下至上共有三套正旋回,水动力由强至弱,为辨状河沉积体系。1 490～1 506 m下部为灰黑色泥岩变为深褐色粉砂岩、灰褐色泥质粉砂岩,还原环境变为氧化及强氧化环境。中部为深褐色细砂岩、灰色泥质粉砂岩,发育板状交错层理,氧化及强氧化环境。上部为灰褐色泥质粉砂岩、深褐色粉砂岩,氧化及强氧化条件,局部见灰褐色泥岩及粉砂质泥岩。由下至上发育七套正旋回和两套反旋回,水动力由强至弱再变强,为辨状河沉积体系。

φ为粒径; λ为面积; μ为均值; σ为方差; M为峰值; C1、C2为次总体1、2; P1/2为交点; S1为重叠面积图5 PL19-3-8ST井1 412～1 426 m基于粒度次总体拟合图的沉积相识别Fig.5 Identification of sedimentary facies based on grain size subtotal fitting diagram from 1 412 m to 1 426 m in Well PL19-3-8ST

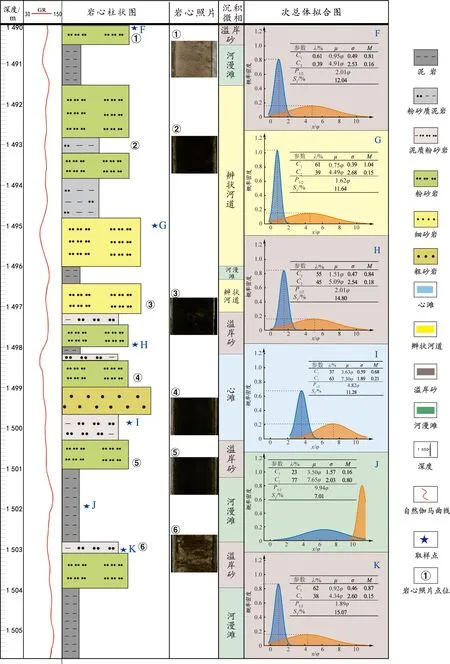
图6 PL19-3-8ST井1 490～1 506 m基于粒度次总体拟合图的沉积相识别Fig.6 Identification of sedimentary facies based on grain size subtotal fitting diagram from 1 490 m to 1 506 m in Well PL19-3-8ST

4 讨论

分析结果显示,A～K的次总体拟合图多为双峰,偶见三峰,粒径分布范围-0.75φ～11.25φ,主峰出现的位置在0.75φ～7.90φ。其中C1、C2(次总体Ck:次总体曲线按照由细到粗的顺序分别命名为C1、C2,…,Ck)的μ、σ、λ、M范围分别为0.75φ～3.94φ,0.39～1.97,23%～67%,0.20～1.04;4.34φ～7.90φ,0.65～2.68,31%～77%,0.15～0.61。C1主要为中砂-粗粉砂,C2主要为粗粉砂-泥。三峰型M1=0.90,M2=0.43,M3=0.19;σ1=0.44,λ1=0.41,μ1=0.89φ,中砂;σ2=0.94,λ2=0.31,μ2=2.26φ,细砂,σ3=2.11,λ3=0.28,μ3=6.68φ,极细粉砂。溢岸砂S1(Sm/n为重叠面积,Sm/n越大,叠合度越高,即粒径差异性越小水动力越近似;反之,水动力能量越复杂。而当μ1与μ2接近,旁瓣和Sm/n较小时,水动力能量反而近似。)整体较高12.04%～15.07%,粒径差异性越小,叠合度较高,水动力环境越近似。辫状河道S1集中11.64%～12.75%,混合度较稳定。心滩S1分布范围较广7.15%～13.50%,即水动力环境可能存在两种,水动力条件近似的下和水动力能力复杂的上游。河漫滩S1为10.57～24.58,J的水动力条件近似,而C的水动力较J复杂。

对比不同沉积环境中的次总体拟合图的特征,发现各个微相的次总体拟合图各参数相互关系与岩性剖面、沉积微相均有很好的匹配性且M1差异明显。整体而言,溢岸砂(F、H、K)中M1集中在0.8～0.9,M2均小于0.20,μ1集中在0.92φ～1.51φ,中-细砂,μ2集中在4.34φ～5.09φ,粗-中粉砂;辫状河道(A、G)中M1分布两个区间0.50～0.60或1.00～1.10,M2均小于0.20,μ1集中在0.75φ～1.34φ,中砂-细砂,μ2集中在2.68φ～5.89φ,细砂-中粉砂;心滩(B、D、E、I)双峰型及三峰型,M1集中在0.60～0.80,M2均在0.20附近,μ1集中在1.42φ～3.63φ,中砂-粗粉砂,μ2集中在5.47φ～7.30φ,中粉砂-极细粉砂;三峰型M1=0.90,M2=0.43,M3=0.19,μ1=0.89φ,中砂,μ2=2.26φ,细砂,μ3=6.68φ,极细粉砂;而河漫滩(C、J)中M1集中在0.2～0.3,M2大于M1,μ1集中在1.57φ～1.97φ,中砂-细砂,μ2集中在7.65φ～7.90φ,极细粉砂-泥。

A、G虽均为辫状河道,但G的M1大于A的M1,其原因可能为G阶段发生一次小规模的洪水事件导致物源供给量短时间的增大,水动力增强,而A的M1均小于心滩(B、D、E、I)的M1,其分选性比心滩差。B、D、E、I虽均为心滩,但I的μ1均小于B、D样本,大于A样本且M1远远大于河漫滩(C、J),粗碎屑颗粒比河漫滩多,I为心滩中细粒成分。E为三峰型,C1、C2、C3各组分混杂堆积,符合心滩粒度变化范围宽,成分复杂等地质认识,E可能为非活动性河道砂坝。C、J 为河漫滩,其M1最小,分选性差,整体粒径较细,水动力弱,主要对应粉砂质泥岩及泥岩。F、H、K整体为细砂～粉砂,岩性剖面观察到顶底岩性突变面,其次总体拟合图形态几乎保持一致,M1集中在0.8～0.9,M2均小于0.20。

从以上分析可以得出,C1为粗碎屑颗粒,C2为较细碎屑颗粒,M1及μ为划分心滩、辫状河道、溢岸砂及河漫滩关键组分,而σ越小,次总体拟合图越窄,M1越高、μ1越小,粗碎屑颗粒值越大,则水动力越强。C2、C3为次要组分,主要营力为悬浮搬运,细碎屑颗粒填充在粗砂孔隙中,粗碎屑颗粒孔隙内水动力减弱,当流水动力不足以克服碎屑的重力时,悬浮的粉砂或黏土在流速减小到一定程度时,便开始沉降并滞留在原处,当M2越高、μ1越大,C2、C3的组分相对较高,则水动力越弱。

5 结论

提出了一种快速有效的 GMM粒度数据拆分新方法,在一定程度上解决了粒度曲线模拟过程中无法分离、提取与沉积过程相关的粒度分布次总体的问题,实现粒度资料的无监督自动聚类,准确识别正态母体的个数,精确获得数学参数并定义其地质含义。

将GMM应用至渤海湾盆地馆陶组,该地区共有2种次总体组合样式,K=2的双峰型及K=3的三峰型,其中M1及μ为划分心滩、辫状河道、溢岸砂及河漫滩关键组分,σi越小,Mi越高,μi越小,即次总体的图像越窄,μi对应的碎屑含量越多,分选性越好,水动力越强。C2、C3为次要组分,M2越高、μ1越大,C2、C3的组分相对较高,水动力越弱。

次总体拟合图的各参数相互关系反映的水动力条件与岩性剖面、沉积微相均有很好的匹配性,故该图件在实际应用中具有良好的适用性并提高水动力条件识别效率和精度。