基于响应曲面法的割缝筛管结构参数优化

2024-01-12吴欣袁田浩杨文领王玥张恒

科学技术与工程 2023年34期

吴欣袁, 田浩*, 杨文领, 王玥, 张恒

(1.四川轻化工大学机械工程学院, 宜宾 644005; 2.中国石油集团渤海钻探工程有限公司, 天津 300280)

随着油田开采的不断深入,地层能量随之减弱,井内压差不断增大,进而导致地层出砂的问题愈发频繁。地层出砂若进入井筒,可能会造成管路堵塞、泵损坏、井壁坍塌、套管损坏,甚至油井报废等严重事故。常见的防砂措施有化学防砂和机械防砂两大类。

其中机械防砂主要有:砾石填充、割缝筛管、绕丝筛管、预填充筛管等。砾石填充在大斜度井、水平井中易填充不均匀,防砂效果不理想[1]。绕丝筛管、预填充筛管等结构复杂,较割缝筛管成本高[2]。因此割缝筛管技术自应用以来,由于其经济性好、适用范围广、防砂效果好等优点,在完井防砂中得到了广泛应用[3-6]。但由于砂堵、筛管长期承受的地层围压等因素的影响,使筛管出现压溃变形导致筛管失效[7-8]。筛管的变形程度会直接影响防砂效果,确保筛管有足够的强度是保证井筒安全和防砂质量的基础。文献[9-14]从割缝筛管防砂失效的原因研究如何提高割缝筛管防砂效果和生产能力。

王晶等[15-16]从固定外载下最大应力大小研究筛管强度;高定祥等[17]用筛管应力达到屈服强度时所受外载大小来研究筛管强度;Dastgerdi等[18]用筛管冲孔前后强度降低比值研究筛管强度;李航等[9]从缝槽棱边应力分布情况研究筛管强度;何良等[11]用割缝处变形量研究筛管强度;彭玉丹等[7]、付光明等[8]和Marbun等[19]用筛管发生压溃变形时的临界压溃强度研究筛管强度。

黄勇等[10]和Yang等[20]得出筛管强度的方法主要与筛管应力大小有关,未研究筛管应力分布情况,但筛管应力分布情况特殊,不符合实际情况;董长银等[6]、李航等[9]、胡成等[12]和高定祥等[17]分别用缝槽棱边应力分布、割缝变形情况、筛管压溃时应力研究筛管强度,均与筛管应力分布特点有关,但不能详细描述筛管的变形情况。

以上研究在割缝筛管的强度、防砂能力、参数选择等方面进行了深入探讨,为割缝筛管的应用提供了理论基础,但未能形成一个有效的最优化割缝参数方法。现根据割缝筛管应力分布情况,提出使用高应力区域占比来判断筛管总体应力水平;并采用三因素两水平的响应曲面法研究各种参数对强度和过流面积的影响规律,推导出二次多项式数学模型,得出限定条件下割缝参数的最优值。

1 模型构建

割缝筛管结构设计的主要目的是根据工作环境在割缝筛管防止出砂和允许产液的范围内,选择适当的结构参数组合以实现保持井筒稳定性、最低压降、最大生产流量以及保证防砂效果[10,21]。在水平井中管柱结构如图1所示。

图1 水平井割缝筛管示意图Fig.1 Schematic diagram of slotted screen in horizontal well

1.1 模型简化

由于筛管井下工作环境复杂,难以量化,对模型进行如下假设:①忽略割缝筛管的材料、加工等缺陷;②忽略割缝筛管其他生命周期的残余应力的影响;③忽略地层应力的不均匀情况及变化。

根据割缝筛管损坏情况,对生产过程中的割缝筛管进行受力情况分析。将筛管外载简化为15 MPa的大地围压。根据筛管安装方式,固定设置为筛管端部轴向位移为0 mm。

1.2 结构参数

缝宽是筛管根据实际工作环境在一个范围值中选择的结果,根据地层情况选择筛管缝宽为0.42 mm。建立割缝筛管三维模型,选定要研究的布缝参数为周缝数(即圆周一圈上割缝的数目)、缝间距和缝长。具体结构参数取值范围如表1所示。

表1 结构参数Table 1 Structural parameters

割缝筛管材料为P110,其材料属性如表2所示,材料应力应变曲线如图2所示。

表2 材料属性Table 2 Material properties

图2 材料应力应变曲线Fig.2 Material stress-strain curve

1.3 网格划分

割缝筛管整体(管体)尺寸与局部特征(缝)尺寸相差较大,若建立筛管整体模型,将导致网格划分困难,计算难以收敛。因此根据筛管结构特点对有限元模型进行必要的简化。由于缝端部会发生应力集中,对缝端处进行网格细化。简化模型如图3所示,模型完整网格包含40 104个域单元、17 850 个边界单元、 2 084 个边单元以及564 327个求解的自由度数。

图3 简化模型及网格划分Fig.3 Simplified model and grid division

根据模型结构特点,有限元模型边界条件设置如图4所示:设置外压15 MPa,设置固定方式为端面轴向位移为0 mm,在模型简化切面处设置对称,其余边界自由。

图4 有限元结果Fig.4 Finite element results

2 有限元结果

当筛管结构参数为nF=24、S=15 mm、LS=40 mm时,有限元计算结果如图4所示。局部最大应力为758.3 MPa,已超过材料屈服强度758 MPa,但筛管无明显变形。该模型中应力超过材料屈服强度的应力区域体积与总体积的百分比<1%,筛管整体变形量小,仍能满足筛管正常生产防砂与强度需求。分析出现这种情况是因为筛管局部特征远远小于筛管整体尺寸,导致割缝处存在应力集中的情况。而事实上,在微小区域中存在超过屈服强度的应力并不会导致整体结构的崩溃,不影响筛管正常生产工作。

固定筛管nF为84,S为15 mm,LF按range(40,15,100)变化,研究筛管的应力变化情况,结果如图5所示。

图5 计算结果Fig.5 The results of calculation

由图5可知,随着缝长的增大,局部最大应力变化较均匀,但高应力区域占比出现40～70 mm缓慢增长,70～100 mm激增的现象。所以,仅用最大应力来描述筛管的安全程度是不全面的。

3 分析

综上可知,仅使用最大应力不能准确描述筛管的应力水平,还需要从筛管整体应力分布情况判断筛管强度是否满足使用要求。针对上述情况,本文研究提出了使用高应力区域占比来描述筛管整体应力水平的方法。

3.1 研究方法

3.1.1 高应力区域占比

由于割缝筛管缝端处应力集中情况严重,导致筛管最大应力极易超过材料屈服强度。使用高应力区域占比Q来描述筛管的安全程度。定义高应力区域占比Q为:筛管上超过材料屈服强度的应力区域所占筛管总体积的百分比。高应力区域占比计算公式为

(1)

式(1)中:Q为高应力区域占比,%;V屈为模型中应力大于等于材料屈服强度的体积部分,mm3;V为模型总体积,mm3。

3.1.2 单位长度过流面积

使用单位长度过流面积S来描述筛管的生产能力。定义单位长度过流面积S为:每米筛管内壁圆柱面上割缝的投影面积大小。单位长度过流面积计算公式为

(2)

(3)

S总=S排缝×N排数

(4)

式中:S排缝为每排缝过流面积,mm2;N排数为单位长度割缝排数,1;S总为单位长度过流面积, mm2/m。

3.2 单参数影响分析

3.2.1 周缝数的影响

取S=15 mm、30 mm、45 mm,LF=100 mm,nF按range(24,6,84)变化,计算结果如图6所示。

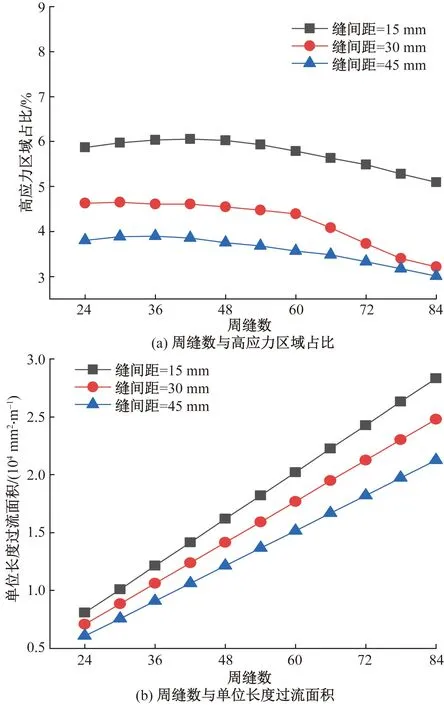
图6 周缝数对各指标的影响Fig.6 The influence of the number of weekly slits on each indicator

由图6(a)可知,随着nF的增加,高应力区域占比下降速度呈先慢后快的趋势。当nF在24～48范围内,高应力区域占比随nF增加但无明显变化,nF在48～84范围内高应力区域占比随nF增加而缓慢下降。由图6(b)可知,随nF增加,单位长度过流面积呈线性增长,S越小增长速度越快。可初步判断,nF是影响筛管生产能力的主要因素,是影响筛管安全程度的次要因素。

3.2.2 缝间距的影响

取nF=84、54、24,LS=100 mm,S按range(15,5,45)变化,计算结果如图7所示。

图7 缝间距对各指标的影响Fig.7 The influence of slits spacing on each indicator

由图7(a)可知,高应力区域占比随S增大而减小。当S在15～35 mm范围内,高应力区域占比随S增加而均匀下降,在35～45 mm范围内高应力区域占比下降速度变缓。由图7(b)可知,随着S变大,单位长度过流面积减小,且nF越大,S对单位长度过流面积影响越大。单位长度过流面积在S=15～25 mm与30～40 mm范围内变化不大,是因为当固定LF变化S后,在单位长度内可加工的排缝数(即轴向上可加工缝的数量)主要受S影响,S在一定范围内可加工的排缝数不变,单位长度过流面积大小就不会发生变化,所以单位长度过流面积在S=15～25 mm与30～40 mm范围内变化不大。初步判断,S是影响筛管生产能力与安全程度次要因数。

3.2.3 缝长的影响

取nF=84、54、24,S=15 mm,LF按range(40,15,100)变化,计算结果如图8所示。

图8 缝长对各指标的影响Fig.8 The influence ofslits length on each indicator

由图8(a)可知,不同nF下,LF对高应力区域占比影响规律相同:LF在40～70 mm范围内时,LF对高应力区域占比影响不大;LF在70～85 mm范围内时,随着LF增加,高应力区域占比快速增大;LF在85～100 mm范围内时,随着LF增长,高应力区域占比激增。由图8(b)可知,随着LF增长,单位长度过流面积缓慢增长,但单位长度过流面积整体变化不大,LF对单位长度过流面积的影响不大。图8(b)出现单位长度过流面积在LF=90～100 mm范围内LF增长但单位长度过流面积下降的现象。是因为固定S变化LF后在单位长度内LF增长可加工缝排数减少。当LF足够大时,单位长度筛管受空间尺寸限制,导致出现加工完成后出现较长未加工区域却不足以再加工一排割缝,出现空间浪费。所以出现LF增加而单位长度过流面积下降的现象。初步判断LF是影响筛管生产能力的次要因素,是影响筛管安全程度的主要因素。

3.3 响应曲面法实验设计

3.3.1 影响因素确定

根据单因素分析结果,选择以下3个参数为影响因子:周缝数nF为X1、缝间距S为X2、缝长LF为X3,以高应力区域占比Q为Y1、单位长度过流面积S总为Y2响应变量进行响应曲面法实验设计,如表3所示。试验设计结果如表4所示。

表3 响应曲面法试验设计Table 3 Experimental design of response surface method

表4 响应曲面法试验设计结果Table 4 Experimental design results of response surface method

由表4得多元二次响应曲面回归模型为

根据多元二次响应曲面回归模型进行方差分析,结果如表5和表6所示。高应力区域占比与单位长度过流面积回归模型P<0.000 1,说明模型高度显著,拟合程度高。根据nF、S、LF三个影响因子的P判断各影响因子对高应力区域占比与单位长度过流面积的影响显著程度。影响因子对高应力区域占比的影响程度由大到小为:LF>S>nF;影响因子对单位长度过流面积的影响程度由大到小为:nF>S>LF。方差分析结果与单参数分析结果一致。

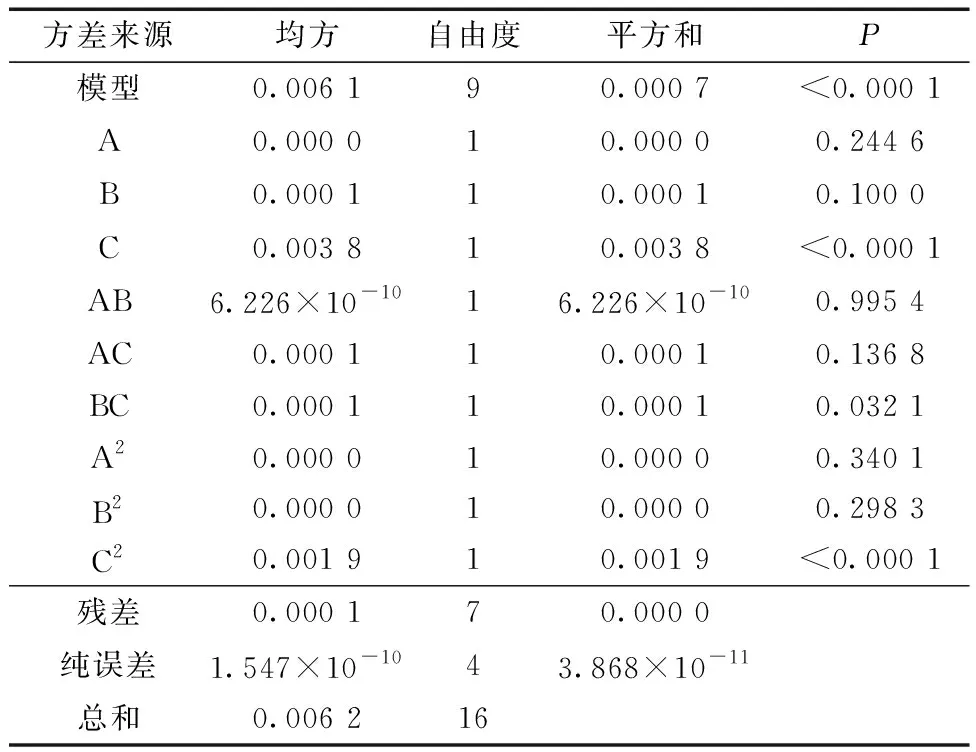
表5 高应力区域占比回归模型方差分析结果Table 5 Results of ANOVA of the highly stressed region proportional regression model

表6 单位长度过流面积回归模型方差分析结果Table 6 Results of ANOVA of the unit length overcurrent area regression model

且高应力区域占比与单位长度过流面积回归模型精密度分别为18.103 8与87.731 4,均大于4,说明拟合模型可靠度较高,能用于指导进行结构参数优化。

3.3.2 响应面分析

根据实验结果与响应曲面回归模型,做出响应曲面图分析响应变量:屈服体积百分比Y1、单位长度过流面积Y2。结果如图9和图10所示。由图9和图10可知,各响应曲面变化趋势与折线图变化趋势相同。

图10 单位长度过流面积Fig.10 Production capacity per unit length

根据响应曲面与响应曲面回归模型分析,以最大化单位长度过流面积并限制高应力区域占比范围为条件进行对结构参数进行优化。求解回归模型得出最优化结构参数组合为nF=75、S=15 mm、LF=68.738 3 mm,响应变量高应力区域占比=0.019 994 2%、单位长度过流面积=24 582.2 mm2/m。

3.3.3 优化结果与试验对比

对优化结果就近圆整取结构参数为nF=75、S=15 mm、LF=68.5 mm。为验证实验结果准确度,以最优化结构参数组合进行有限元分析,有限元结果如图11所示。如图11所示,最优化结构参数组合在额定压力下最大Von Mises应力较图4无太大变化,但明显整体应力分布情况变化较大,用最大Von Mises应力来判断筛管安全程度是片面的。

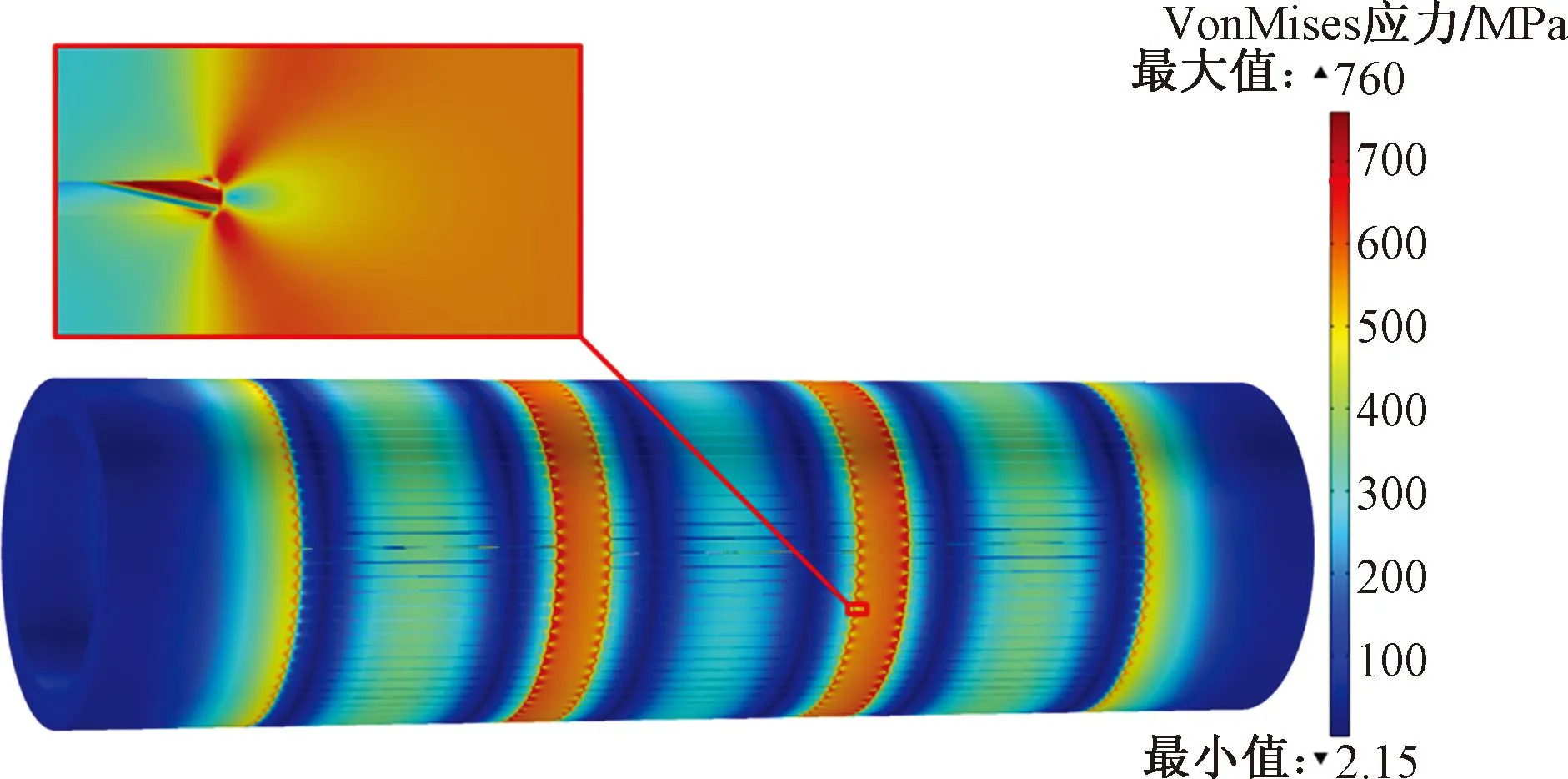
图11 结构参数优化有限元结果Fig.11 The FEM results of structural parameters optimization

对割缝筛管结构参数优化有限元结果与响应变量优化结果进行对比,结果对比如表7所示。有限元计算结果显示高应力区域占比=0.020 204%、单位长度过流面积=23 849.55 mm2/m。仿真结果与优化结果误差分别为屈服强度百分比=1.049 816%、单位长度过流面积=2.980 413%。误差均小于5%,满足精度要求。