基于网络能耗与交通效率的多子区控制模型

赵 刚，陈 森，张卫华

（1.深圳市市政设计研究院有限公司，广东 深圳518029；2.合肥工业大学汽车与交通工程学院，安徽 合肥 230009）

0 引言

近年来，由于中国城市化进程的快速推进和汽车使用率的增加，使得城市中交通拥堵现象屡见不鲜。交通拥堵不仅增加了交通能源的消耗和尾气排放，造成了周围环境的破坏[1]，而且还会大大增加居民的出行时间，并导致驾驶员感到烦躁和愤怒，损害其健康。由于交通控制具有快速、经济、安全等优点，其逐渐成为解决交通拥堵的有效途径。按照控制范围，交通控制可以分为区域信号控制、干线信号控制和单点信号控制；按照控制方式，交通控制可由自适应控制、感应控制和定时控制三种控制方式组成，而这些传统控制方式的交通流模型都是依据城市路网OD分布而建立的，建模过程非常复杂[2]。

自2007年MFD理论的提出，证实以及其应用范围的不断拓展[3～9]后，由于MFD阐述的是路网宏观层面上交通流三参数之间相对稳定的特性，无需了解路网内部各路段微观交通流信息，一些学者利用MFD特性来进行交通控制研究，以此来解决交通拥堵，并取得了相对丰硕的研究成果。Keyvan等[10]提出单区域过饱和网络反馈阀门控制方法，利用研究路网MFD理论的特性，通过在研究路网边界设置控制“阀门”来减少交通拥堵，提高交通效率。Haddad等[11]提出了鲁棒周边控制方法，在控制模型设计中不仅考虑流入研究路网的车辆数，而且考虑了流出研究路网的车辆数，设计出的R-PI控制器也综合考虑了输入和输出双重干扰，综合调节流入率和流出率来确保路网车辆完成率最大。Kouvelas等[12]在Mehdi等人的基础上针对较大面积研究路网提出了多子区的反馈闸门控制方法，并在案例中与单子区作对比研究，验证了其控制效果更好。但是针对较大区域路网，并没有利用MFD特性综合考虑控制燃油消耗和交通效率两个目标的研究。

为提高较大区域研究路网的车辆交通运行效率，并降低其交通能源消耗，本文将利用MFD特性建立面向多子区网络能耗与交通效率的双目标规划模型，采用Fminion函数进行求解，并提出MFC-PI阀门控制方法将两个目标控制在最优解附近。

1 面向多子区网络能耗与交通效率的双目标规划模型

1.1 目标1——多子区网络车均燃油消耗

以文献[13]中单子区车均燃油消耗模型为基础，基于MFD特性可建立多子区车均燃油消耗模型。见下式（1）：

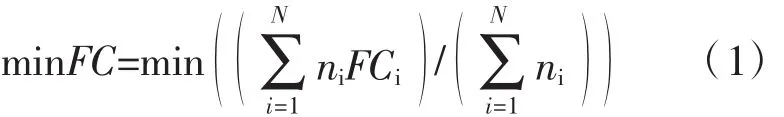
式中:FC为整个网络内车均燃油消耗，L/100kM；ni为第i个子区内移动的车辆数，veh；FCi为第i个子区网络内车均燃油消耗，L/100kM。

其中，FCi主要由路段燃油消耗[14]与交叉口燃油消耗[15]两部分组成，参考文献[13,16]的研究成果，子区i可建立以网络车辆数ni为自变量的车均燃油消耗模型，见下式（2）：

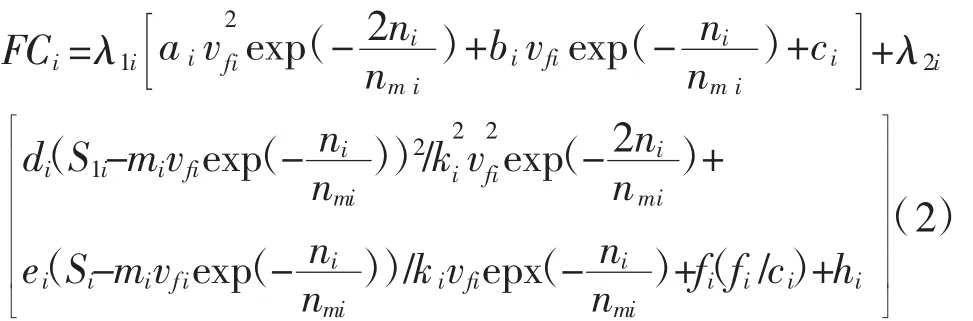
式中：ai，bi，ci分别为第i个子区路段燃油消耗的拟合参数；vfi为第i个子区的路网自由流平均速度，km/h；nmi为路网阻塞车辆数，veh；mi，ki分别为第 i个子区路段行程时间和路段上游交叉口饱和度模型的拟合参数；di，ei，fi，hi分别为第 i个子区交叉口燃油消耗模型的拟合参数；qi/Ci为第i个子区的交叉口平均饱和度；gi/ci为第i个子区的平均绿信比；S1i为第i个子区的两交叉口之间的路段平均长度，km；λ1i，λ2i分别为第i个子区路段和交叉口燃油消耗模型的权重系数，具体取值可根据实际路网中交叉口长度和基本路段长度来确定。

1.2 目标2—多子区网络车辆完成率

基于MFD特性划分后的各子区应存在相应的车辆完成率模型。将所有子区的车辆完成率累加求和，便可得到整个研究路网的车辆完成率模型，其中 αi，βi，γi，ηi分别为模型中第 i个子区的拟合参数，则表达式见式（3）：

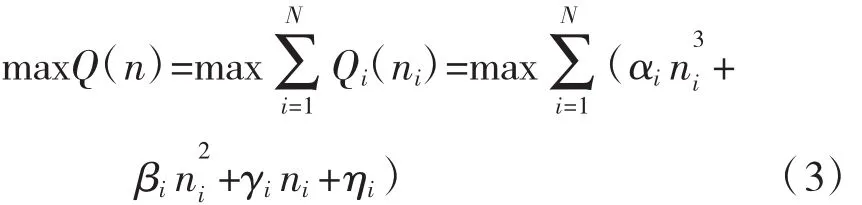
1.3 目标函数求解

为实现整个路网车均燃油消耗最少和路网车辆完成率最大，可建立式（4）目标函数。

由式（4）可知，上述双目标非线性规划模型可利用间接解法求解，即将其转化为单目标规划模型。即在本文中，将研究路网车辆完成率转化为路网燃油消耗的约束条件。可得下式（5）：

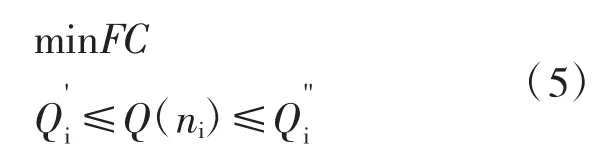
上式可用MATLAB中的fmincon函数求解，具体求解步骤可参考文献[17]。

2MFD控制子区划分及多子区入口边界控制方法

2.1 MFD控制子区划分

当研究路网面积较大时，基于研究路网同质需求和控制效率的考虑，需要将非同质较大区域路网划分为若干个小区域同质路网。参考文献[18]的划分方法，对较大面积区域路网进行同质子区划分，有以下三点划分原则：

（1）为保证边界控制方法的效率，划分后各子区面积宜在3～9 km2，且子区数量不太多。

（2）子区划分边界须为研究路网中的交叉口，划分后各子区的MFD特性应非常明显，即各子区均应存在拟合程度较高的MFD图形，各子区间的密度方差尽量大，子区内部各路段间的方差应尽可能小。

（3）为便于控制方法的提出和执行，划分后各子区在空间上须紧密相连。

2.2 非同质路网的车流平衡方程

把一个非同质网络划分为N个子区，假设每个子区都存在一个理想的MFD，其中i=1，2，…，N表示系统中每一个子区。如图1所示，Qi（ni（t））max表示第i个子区的最大网络车辆完成率，ni，max表示在第i个子区网络内车辆数。

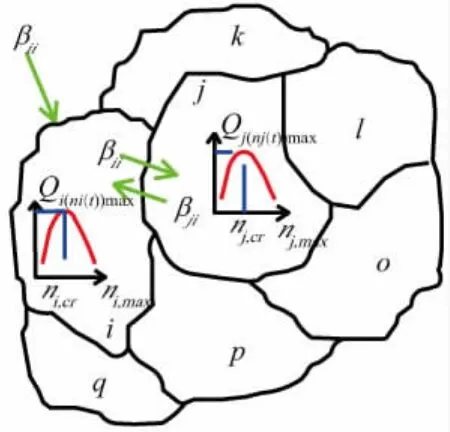
图1 多个MFD子区的非同质路网

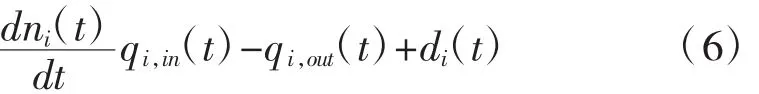
其中：ni（t）为第i个子区t时刻的网络车辆数，veh；qi，in（t）为时刻子区i的流入量，veh；qi，out（t）为时刻子区i的流出量，veh；di（t）为时刻子区i不能控制的网络流入量，veh。

i子区的车流平衡方程可表示为式（6）：

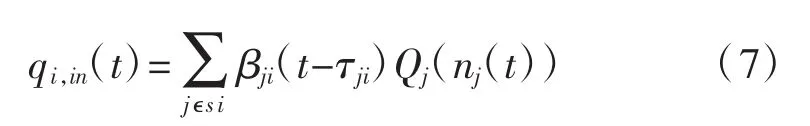
其中:βji（t-τji）为t时刻子区j到子区i的输入变量，可通过周边控制器来计算；τji为车辆从子区j到子区i的旅行时间，h；Sj为子区i的流出量到达的目的子区的集合。

假设τji=0，即当车辆从一个子区流出的时候，它可以立即到达将要流进的子区。因此，将式（7）代入式（6）中，得到非线性状态方程，见式（8）：

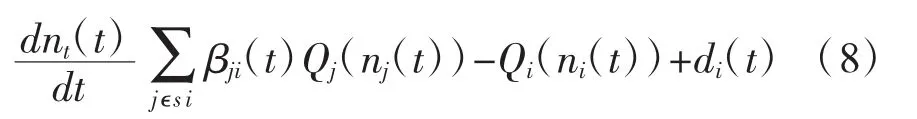
βji（t）为子区j流入子区i的流量占子区j网络流出率的比例；βji（t）Qj（nj（t）为t时刻子区j流入子区i的最优边界流入量，veh；Qi（ni（t）为t）时刻由MFD特性计算出i子区的网络流出率，假设i子区流出量qi，out（t）=Qi（ni（t）），即大小等于子区i流入子区 j的流入量之和，其中 j∈Si。

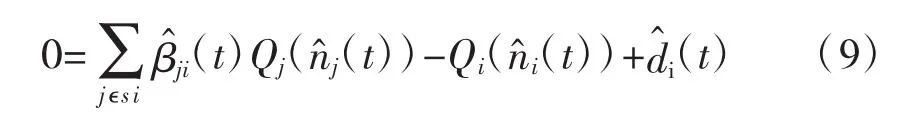
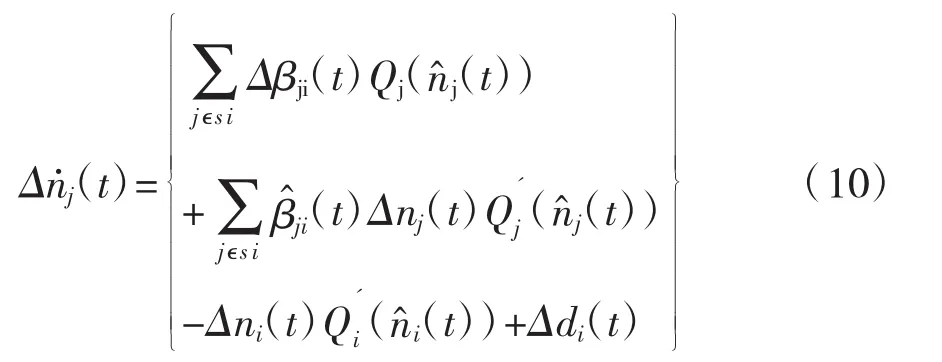
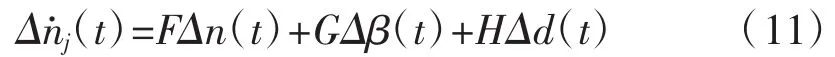
在接近稳态点时，线性系统方程（10）近似等于非线性系统方程（8）。把公式（10）应用到网络的个子区中，向量公式（11）可以描述路网系统随着时间推移而发生的变化。其中：Δn为状态偏差向量，即子区i的向量偏差…，N；Δβ 为控制偏差向量，即子区 i的向量偏差为干扰需求偏差向量，即子区i的向量偏差Δdi=di-；F，G，H 分别为相应的矩阵。

将连续系统用欧拉一阶公式离算化可得式（12）：

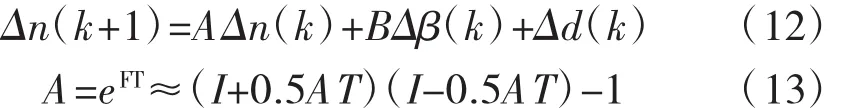
其中：A为离散时间系统的状态矩阵；B为离散时间系统的控制矩阵。

2.3 非同质路网子区PI反馈控制器

将离散线性时间模型式（12）作为反馈控制调节器设计的基础，根据Papageorgiou的研究成果[14]可将式（12）化简得到：

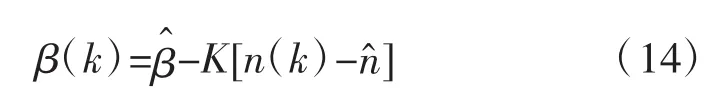
增益矩阵K可由已知矩阵Q，G，Q，R求出，见式（15）：

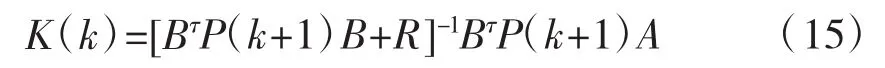
而矩阵P可由差分方程解出：

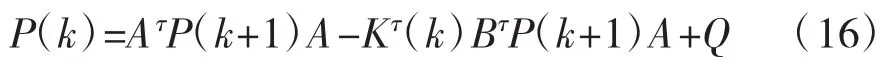
根据文献[19]可将式（14）化简分解为：

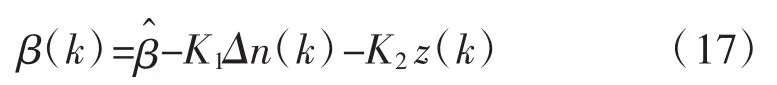
将k+1=k代入式（17）得式：

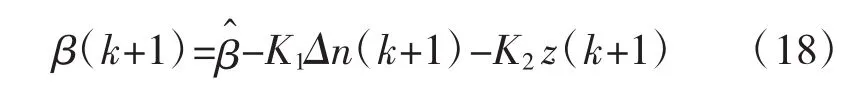
式（18）减式（17）可得最终 PI控制器，如下式（19）：

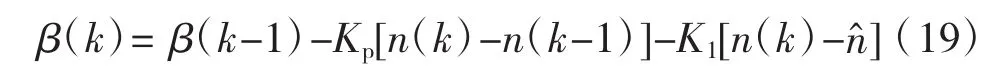
其中：Kp=K1-K2Y为比例增量，K1=K2Y为积分增量，其中通过对离算时间Riccal方程解K的计算可解出K1和K2；＾为双目标规划模型求出的最优解＾=[n1,cr，n2,cr，L，nN,cr]τ。

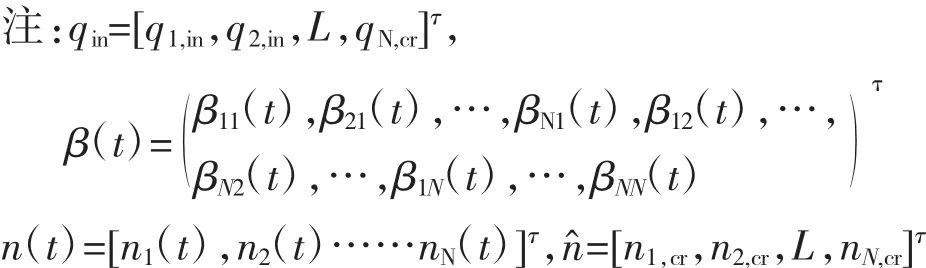
2.4 多子区协调反馈阀门控制方法

面向较大区域的过饱和交通网络，基于特性得到划分后的路网各同质子区，根据反馈阀门控制模型[10]的原理，提出了多子区协调反馈阀门控制方法，该控制方法原理是依据反馈原理和3.3中求得的多子区反馈控制器，对整个研究路网的交通状态进行调控，利用关键路段节点交通检测器反馈的信息，对 qin、n（t）、Q（t）进行监控，通过各子区的“控制阀门”控制 qin，以此来控制 β（t），以达到将各子区的网络车辆数控制在n＾值左右，以此来降低研究路网燃油消耗和提高车辆完成率。基于MFD的路网反馈控制逻辑如图2所示，其中Kp为PI控制比例系数，KI为PI控制积分系数，qin为网络流入量，n（t）为网络内车辆数，Q（n）为网络车辆完成率，ξ为输出相关系数，d为不受边界控制的随机扰动交通量，qout为网络流出交通量，β（t）为子区边界流率，＾为控制器求得的最优网络车辆数。

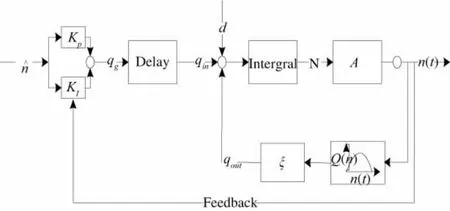
图2 路网反馈阀门控制逻辑图

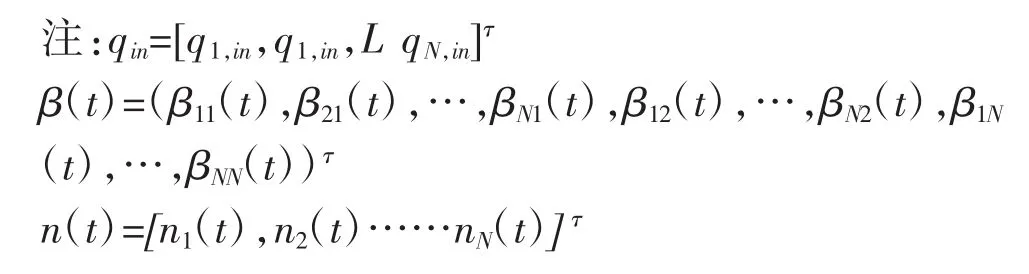
3 实例分析

3.1 路网描述

案例分析选取合肥滨湖部分路网作为研究区域[20]，VISSIM仿真路网如图3所示，该路网为非同质道路路网，利用文献[18]子区划分方法将该路网划分为三个同质小区，路网参数如表1所示。

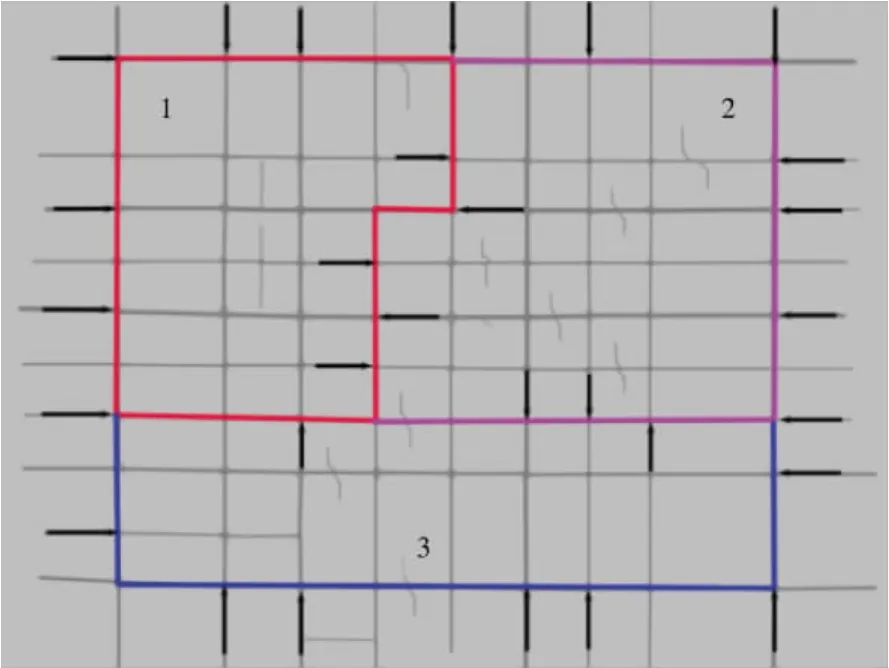
图3 仿真路网示意图

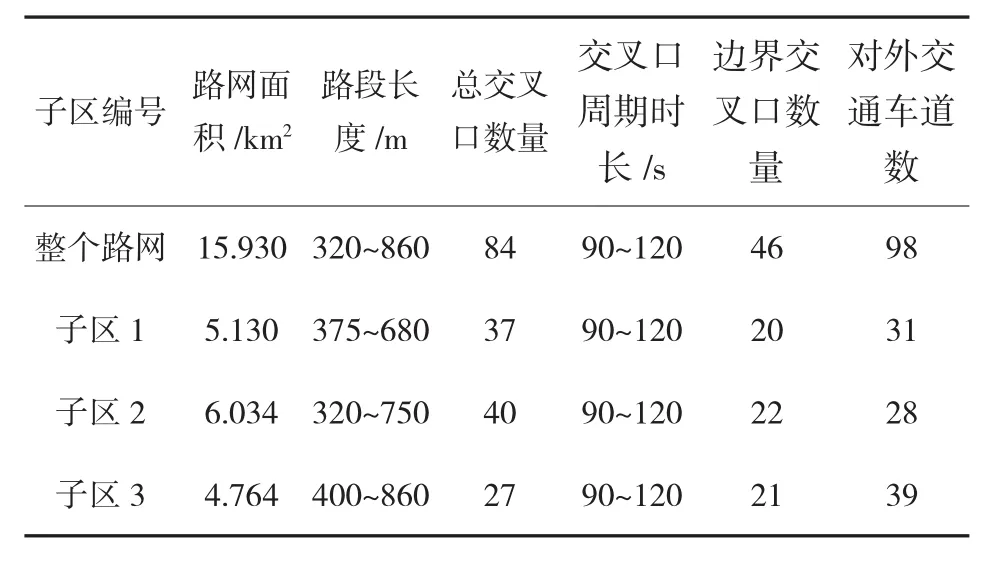
表1 路网子区基本参数

3.2 参数标定

根据VISSIM仿真实验数据，由OEIGIN拟合得到子区划分前整个路网及分区后各个子区MFD

的图和n-v图，如图4所示。

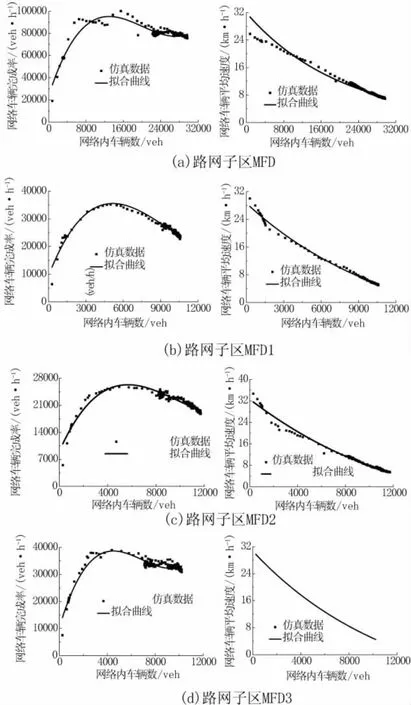
图4 路网子区的MFD图和

整个路网和划分后各个子区的n-v曲线方程系数与MFD曲线方程系数，如表2所示。

通过对研究路网实际情况的分析，并结合VISSIM仿真实验的数据，对整个路网及其子区的燃油消耗模型参数进行标定。相应标定参数分别见表3和表4。

3.3 仿真分析

使用MATLAB软件对2.3节中的双目标规划模型进行求解，由程序运行结果可知，当n＾=[2000，3247，2804]τ时，这时整个路网内车均燃油消耗最低，即11.1808L/100kM，而各个子区的车辆完成率也维持在一个比较高的值。

仿真总时长设定为240 min，初始时刻子区1、2、3内的车辆数均为0 veh，交通需求（研究路网外至研究路网内）为120 veh/min。为了模拟平峰—高峰—平峰交通环境，设置仿真前90 min内交通需求以3 veh/min的速度增加，后150 min内交通需求以3 veh/min速度减少。子区路网1、2、3可以容纳最大车辆数分别为 12 000 veh、12 000 veh、9 000 veh，“控制阀门启动值”分别为2 000 veh、3 250 veh、2 805 veh。在无控制和MFC-PI阀门控制下，三个子区的路网内车辆数和路网车辆完成率的变化关系如图5所示。

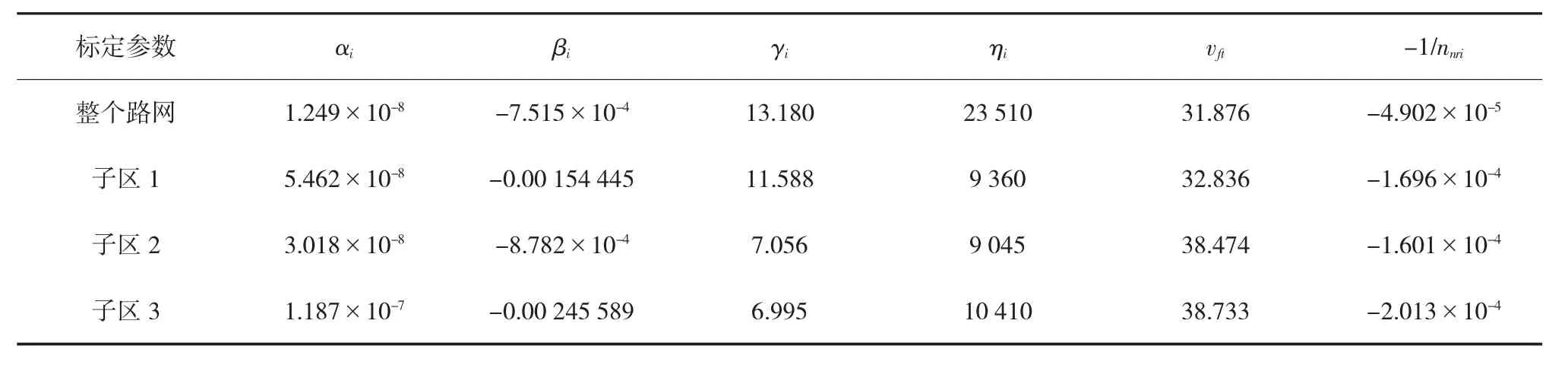
表2 路网子区MFD和n-v曲线参数

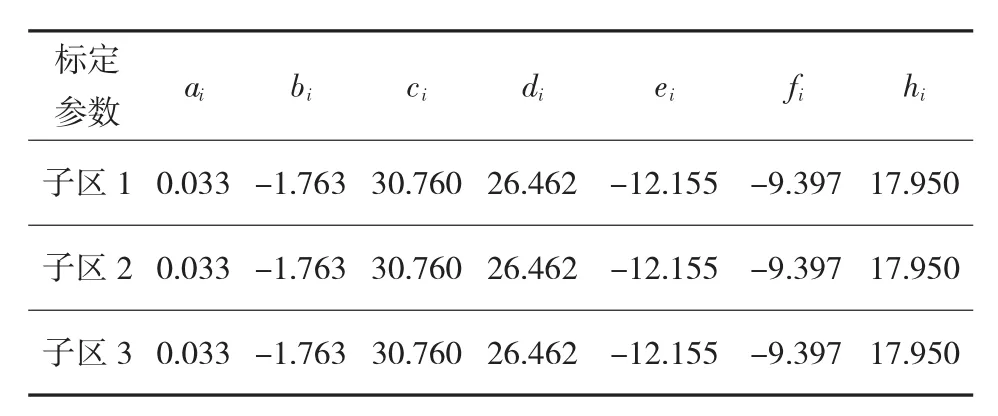
表3 基本路段车均能耗模型参数与交叉口车均能耗模型参数标定

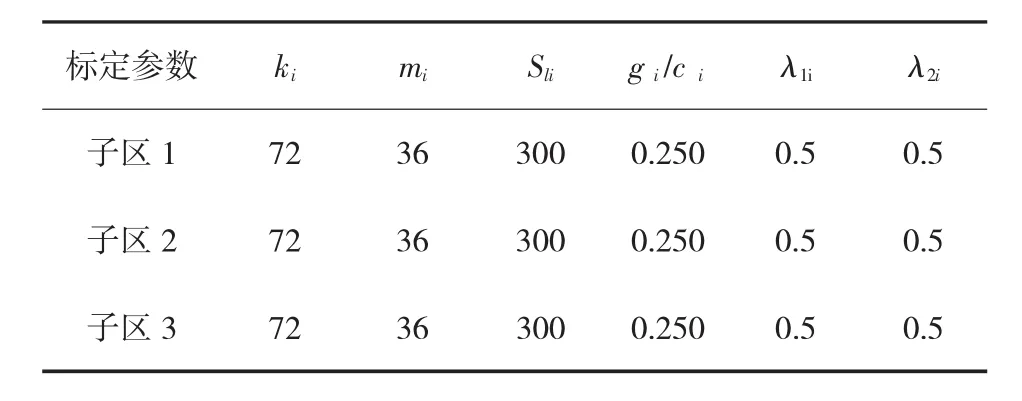
表4 其它相关参数标定

在无控制条件下，从图 5（a）（c）（e）以及图 5（b）（d）（f）中可以看出，在前 60 min 内，各子区路网内的车辆数和车辆完成率都是随着仿真时间增加而增多，这是因为此时路网未达到饱和状态，而交通需求逐渐增加所致，子区1、2、3分别在t=53 min，t=50 min，t=45 min达到各自子区的最大通行能力，即此时各子区的车辆完成率最大（可以达到35 534 veh/h、26 284 veh/h、38 648 veh/h），而后随着交通需求的继续增加，各子区开始拥堵，路网车辆完成率也开始下降。而在t=90 min时，随着各子区交通需求的降低，子区拥堵逐渐消散，路网车辆完成率又会逐渐增加。

在 MFC-PI控制条件下，由图 5（a）、（c）、（e）以及图 5（b）、（d）、（f）可知，三个子区的路网车辆数分别在（t=21 min、t=40 min、t=38 min）时达到（2 076 veh、3 310 veh、2 873 veh），此时各子区的路网车辆数均超过各子区的“控制阀门启动值”，各子区开启MFC-PI阀门控制器，控制路网车辆数在“控制阀门启动值”附近，以使得路网各子区车辆完成率维持在一个比较高的水平。子区1、2、3分别在 130 min、131 min、150 min 时，因为各子区交通需求的降低，使得各子区路网车辆数开始减少，各子区路网车辆数低于“控制阀门启动值”，关闭MFC-PI阀门控制器，而后子区1、2、3的路网车辆完成率也逐渐减少。

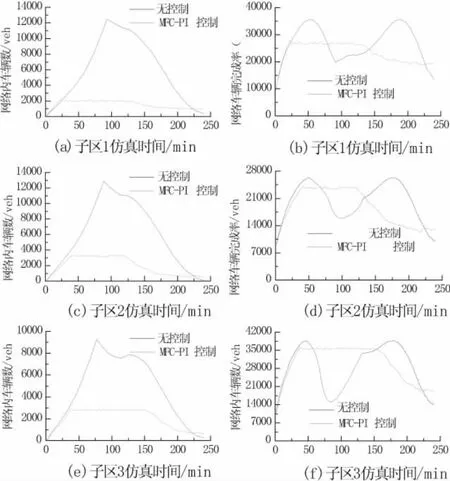
图5 宏观路网参数关系对比

无控制和MFC-PI阀门控制下，百公里车均燃油消耗的变化关系如图 6 所示。图 6（a）（c）（e），无控制条件下，仿真前（16 min、17 min、17 min）内，随着交通需求的增加，各子区路网车辆数会逐渐增加，使得其车辆平均速度逐渐减少，相应各子区百公里车均燃油消耗下降。三个子区分别在（t=16 min、t=17 min、t=17 min）时，各子区百公里车均燃油消耗最低，（即此时各子区车辆平均速度达到“经济车速”）。而后随着仿真的继续，路网车辆数继续增加，各子区车辆平均速度脱离“经济车速”，百公里车均燃油消耗开始增大，直至t=90 min时，各子区百公里车均燃油消耗达到最大。而后各子区百公里车均燃油消耗也开始降低，这是由于此时交通需求下降所致。图 6（b）、（d）、（f）显示，在 MFC-PI控制条件下，各子区的车辆数维持在“控制阀门启动值”附近，相应各子区百公里车均燃油消耗也比较低。

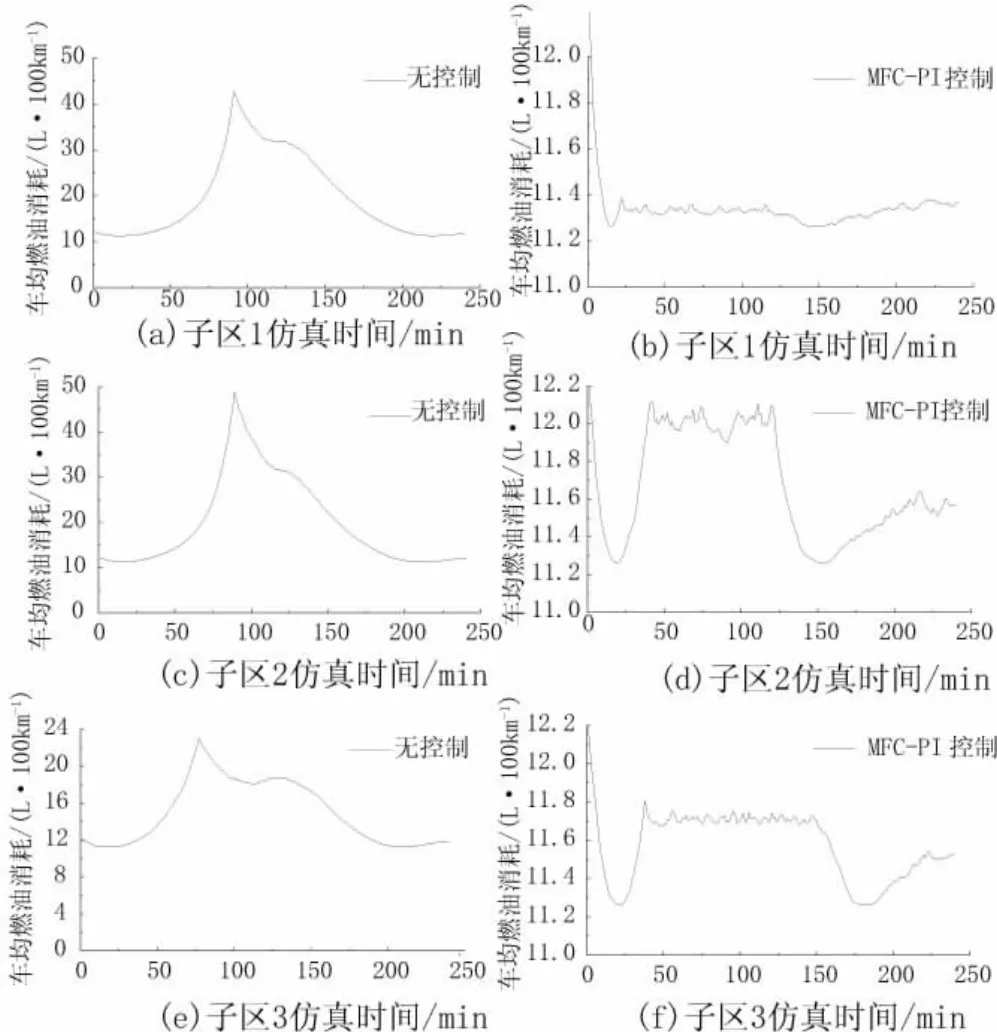
图6 百公里车均燃油消耗

4 结论

从城市路网交通控制的角度，本文综合考虑了较大区域路网的车均燃油消耗和车辆完成率，基于区域MFD特性建立了双目标规划模型，并使用fminion函数对规划模型进行求解。经过仿真实验表明，基于MFD特性的MFC-PI控制方法不仅能够有效的提高路网的车辆完成率，而且可以降低燃油消耗，提高交通运行效率。同时规划模型和控制方法的提出还可以为交通管理和交通能源总体控制决策提供参考。