基于狄利克雷问题的路网控制子区动态划分
2020-12-16阎高伟
张 曼,闫 飞,阎高伟,李 浦
(太原理工大学 电气与动力工程学院,太原 030024)
0 概述
城市规模的迅速扩张使路网复杂性日益增加,针对交通拥堵的演化研究由此得到广泛关注。然而对单路段拥堵状况的研究难以适应相邻路段拥堵时的传播和消散特性[1]。将路网划分为不同拥堵程度的控制子区,能够可视化地显示实时的拥堵场景,这体现了路网控制子区动态划分的重要性。
目前,对于路网控制子区的划分方法已有一些相关研究[2-3]。研究者通常运用谱图理论[4]或归一化分割(Normalized cut,Ncut)算法[5]求解矩阵特征系统,从而将异构路网划分为密度均匀的控制子区,但此类方法的划分性能对参数值较为敏感。文献[6]运用遗传算法与降维处理方法构建一种控制子区快速划分模型。文献[7]考虑拥堵的传播特性构建一种相似性模型,将高相似性的路段聚类成簇。文献[8]将大型路网转化为密度峰值图,并运用图切割算法实现控制子区划分的快速寻优。文献[9]在Ncut算法的基础上构建具有最优宏观基本图的控制子区划分模型,但其获取的子区边界存在不平滑情形。文献[10]基于λ-连通性的概念提出一种启发式划分算法,并执行边界调整程序得到具有光滑边界的控制子区。文献[11]将路段间的拓扑特性融入K均值聚类算法中,弥补了必须对不平滑子区再根据连接性微调的不足。
上述方法实现了路网的静态划分,但未考虑子区在时间维度上的动态演化。文献[12]研究拥堵路段的时空关系,根据前一时刻的划分结果,通过目标函数最小化对后一时刻的高异质性路段进行合并或分割。文献[13]采用一种两层划分方法,通过增量地更新控制子区来跟踪拥堵的传播,该方法与每一刻都重新执行路网控制子区静态划分的方法相比具有更高的效率。
本文考虑路段的密度分布与交通流的时变特性,设计一种新的控制子区动态划分算法。利用路段与其邻域内其他路段的相似度重新定义局部密度概念,确定控制子区划分方案,并对孤立路段进行再处理,实现聚类与连通性的同步约束。在此基础上,将狄利克雷问题求解模型融入算法中,迭代更新高异质性路段的划分结果,从而捕捉子区的演变趋势,实现控制子区的动态划分。
1 狄利克雷问题求解模型
构建一个路网无向图G=(V,E),其中,节点V={v1,v2,…,vi,vj,…,vm}表示m条路段,边集合E={eij}表示所有路段间的n个交叉口。令si、sj表示路段vi、vj的饱和度,则路段vi、vj间的相似度w(i,j)定义如式(1)所示:
(1)
本文设置参数σ=0.1,并构建相似度矩阵W={w(i,j)}m×m。度矩阵D的定义如式(2)和式(3)所示:
D=diag{di}
(2)

(3)
人为设置控制子区数k,以适应交通量的时空分布。定义路网中控制子区的编号为G={G1,G2,…,Gk}。路网无向图上狄利克雷问题的求解模型可看作是根据调和函数(定义如式(4)所示)求解路段对于各控制子区的概率矩阵r,其中,r(i,k)表示vi属于子区Gk的概率。

(4)
由于拉普拉斯方程是狄利克雷积分的拉格朗日方程[14],因此拉普拉斯方程满足边界条件2r=0。定义(n×m)阶的路段关联矩阵,如式(5)所示:
(5)
定义(n×n)阶的0-1对角矩阵C,则拉式矩阵可计算为L=ATCA,调和函数可分解为式(6):
(6)
由于L是半正定的,因此D[r]具有唯一的极小临界点。将路网内的路段分为2个部分,即划分到控制子区的稳定块VS与未分配路段VU,VS∪VU=V,VS∩VU=∅。求解调和函数的临界值,即在确定稳定块的情况下求解未分配路段属于不同子区的概率。假设L和r中控制子区的稳定块为第一部分,未分配路段依次排序在后,则调和函数可分解为式(7):
(7)
求D[rU]关于rU的倒数,并找到临界点:
BTrS+LUrU
(8)

(9)
对未分配路段对应的子矩阵rU进行求解,任意vi属于各子区的概率之和满足式(10)。获取第(i-S)行(i∈{S+1,S+2,…,m})最大值的所在列l∈{1,2,…,k},即将vi划分到子区Gl内。

(10)
2 控制子区静态划分
本节基于密度峰值理论,重新定义了局部密度概念,用于自动识别控制子区的稳定块,同时运用狄利克雷问题的求解模型实现控制子区的划分。子区划分流程如图1所示。

图1 控制子区划分流程Fig.1 Partition procedure of control sub-regions
2.1 局部密度定义
由于交通路网属于稀疏网络,因此本文对传统局部密度概念中节点的度进行加权,运用路段与其邻域内其他路段的相似度来求解局部密度,使之适用于实际路网。
基于密度峰值理论[15],将任意路段vi到每一个更高局部密度路段vj的最短路径记为pij,并将其中的最小值记为pi。局部密度ρi的定义如式(11)和式(12)所示:

(11)
(12)
其中,θ是一个截断阈值,ρi表示在vi的邻域内其他点与该点大于θ值的相似度之和。上述局部密度只对θ的相对大小敏感,说明基于局部密度的划分算法具有很好的鲁棒性。θ的敏感度分析详见本文第4节。
2.2 控制子区稳定块识别
控制子区稳定块识别算法步骤如下:
输入路段集合V,局部密度集合{ρ1,ρ2,…,ρm}


步骤2若任意多个质心在空间上相邻,则只保留局部密度最大的质心,依次选择高局部密度的路段作为新的质心。循环该过程,直到所有质心互不相邻。此时,保证质心周围是低密度路段,以避免质心选取到异常点。若获得的质心数小于k,则返回步骤1,重新赋k值。
步骤3计算剩余的任意路段vi到各质心的最短路径。若pi=pij=1,则将vi归属于质心vj所在的稳定块;若vi与多个质心的最短路径均为1,则将其归属于与之具有最大相似性的质心所在的稳定块;否则跳过该路段,重复此步骤,直到遍历完所有路段,稳定块集合的更新结束。
通过改进的局部密度概念,算法能够自动获取具有最大密度峰值的k个质心并识别控制子区的稳定块,然后将稳定块作为输入参数进行静态划分模型的求解。
2.3 基于狄利克雷问题的控制子区静态划分
狄利克雷问题的求解模型能够解决子区内的最大关联性辨识问题[16]。本节将改进的局部密度概念运用于求解模型中,达到将高相似性路段聚类成簇的目的。
控制子区静态划分算法步骤如下:

输出子区划分结果G={G1,G2,…,Gk}
步骤1将路网内路段分为VS(划分到子区的稳定块)与VU(未分配路段),通过求解狄利克雷问题,对VU内的元素进行划分。

(13)
步骤3将具有最大紧密度的路段划分到对应子区内。若路段与多个子区具有相同的最大紧密度,则任选其一,并重复此步骤,直到所有的子区内部连通时,静态划分结束。
步骤2和步骤3是针对算法在执行控制子区划分时缺乏考虑路网拓扑结构及子区平滑性的不足,进行子区平滑性优化的过程。
2.4 评价指标
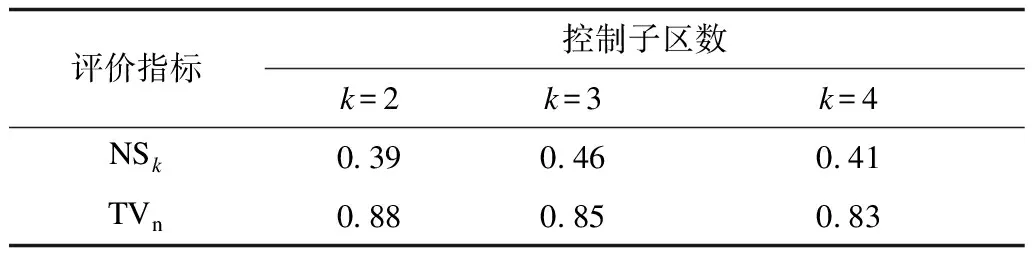
将子区内部匀质性的均值NSk[17]与归一化总方差TVn[7]作为评价指标,对比不同分区下的路网划分性能,定义如式(14)~式(17)所示。两者的取值越小,表明划分效果越好。
(14)
(15)
(16)
(17)
其中,ab(Gl,Gk)=1表示控制子区Gl、Gk相邻,NGl表示子区Gl内的路段数。
3 控制子区动态划分
由于交通量动态分布,若对每一时刻的路网都执行静态划分,计算复杂性较高,因此本文提出一种动态划分算法存储前一时刻稳定路段的划分结果,同时对异质性高的路段进行微调,从而得到后一时刻较好的划分结果,准确捕捉控制子区的演化趋势。
本文提出的动态划分算法采用迭代的聚类过程。在初始时刻t控制子区静态划分结果的基础上,计算各子区(t+1)时刻的饱和度均值,并更新相似度矩阵,取饱和度与所在子区饱和度均值差异最小的路段作为新的质心,以识别(t+1)时刻控制子区的交通状态。在此基础上,将质心作为初始的稳定块,迭代地捕捉与稳定块具有最大相似度wmax的路段,并将其添加到稳定块集合中。需要注意的是,稳定块必须包含在该子区内。但随着迭代次数的增多,该块的异质性呈非线性增长趋势。因此,此处设置限制条件wmax>δ,使得稳定块达到一定覆盖率时截止扩展并缩短运行时间。本文设置δ=0.3。最后利用控制子区静态划分算法对剩余路段进行划分。动态划分算法仅将异质性高的路段作为研究对象,降低了计算复杂性,具体描述如下:
算法动态划分算法
输入控制子区数k,终止时刻t′,局部密度{ρ1,ρ2,…,ρm},ρ1>ρ2>…>ρm
输出路网划分结果G={G1,G2,…,Gk}
1.For i∈[1,k] do//t时刻稳定块识别
3.End For
4.For i∈[k+1,m] do
5.If (pi=pil=1) then
7.Elseif (pi=pil=…=pik=1) then
8.w(i,l)=max{w(i,l),w(i,l+1),…,w(i,k)};
10.Else (pi>1) then
11.++i;
12.End If
13.End For
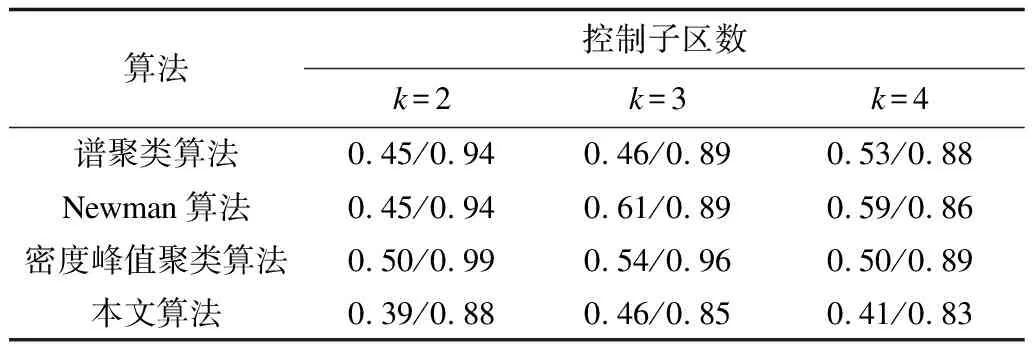
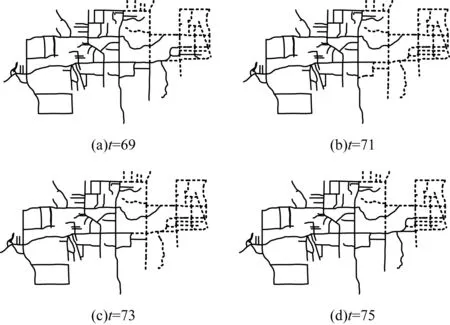
14.While (t 16.If (控制子区内部连通) then 18.Else (存在孤立路段集) then 19.搜索二次划分的目标{vi,vi+1,…,vj}; 22.End If 23.t←t+1//时段更新 24.For i∈[1,k] do 27.End For 28.End While//动态划分稳定块识别 考虑数据与问题来源的真实性,本文以美国法默布兰奇市[18]某区域的真实数据集为例进行分析。该路网包含211条路段,道路拓扑图如图2所示。数据集包含所有路段在2014年10月所有工作日的饱和度均值。本文将全天00:00—23:15的时段取15 min为间隔,得到93个时段,以饱和度为特性进行研究。 图2 美国法默布兰奇市的道路拓扑图Fig.2 Road topology map of Farmers Branch,USA 截断阈值θ是控制子区划分中一个关键参数,其取值直接决定了分区效果。本文选取晚高峰期(t=69)时的路网进行划分。当分区数k=2~4时,θ值对NSk与TVn的影响如图3所示。 图3 2分区~4分区下θ对NSk与TVn的影响Fig.3 Influence of θ to NSk and TVn under two partitions~four partitions 由图3可见,在不同分区数下,NSk与TVn指标值随着θ的增大逐渐变小,表明算法的划分性能逐渐增强。控制子区数k分别为2、3、4时,路网的最优θ值为0.95、0.95、0.25,此时NSk与TVn最小,即算法的划分效果最佳。最优θ值下的路网评价指标如表1所示。 表1 最优θ值下的路网评价指标Table 1 Evaluation index of road network underoptimal θ value t=69时刻的控制子区静态划分结果如图4所示。结合图5中各控制子区内饱和度的频率分布可知:当t=69时,2分区时的子区2内部通畅,多数路段的饱和度集中在0.2~0.5,子区1为饱和区域;4分区下的3、4子区内饱和度相似,但连接两者的公共路段较少,因此,将其划分为两部分。由于执行了子区边界平滑处理,因此各控制子区内部完全连通,为交通信号控制策略提供了准确的依据。 将谱聚类算法、Newman算法[19]、密度峰值聚类算法[20]以及本文算法分别从NSk与TVn两个方面对比算法性能,如表2所示,表中数据均以NSk/TVn的形式列出。 图4 2分区~4分区下控制子区的分布Fig.4 Distribution of control sub-regions under two partitions~four partitions 图5 2分区~4分区下饱和度的频率分布Fig.5 Frequency distribution of saturation under two partitions~four partitions 表2 2分区~4分区下不同算法的评价指标对比Table 2 Comparison of evaluation indexes of differentalgorithms under two partitions~four partitions 由表2可见,在3种分区模式下,本文算法相较其他算法的NSk与TVn值均最小,即控制子区的匀质性最高。其中,2分区时本文算法相较密度峰值算法的NSk、TVn分别降低22%和11%,体现了算法的有效性。 此处分析2分区下t=69~75时段内本文算法与两层动态划分算法的动态划分效果。不同时刻路网的饱和度分布如图6所示,控制子区的划分结果如图7所示。 由图7(a)可见,本文算法与两层动态划分算法[13]在大部分时刻的划分结果相较随着时间的步进一直保持原划分结果的静态划分具有更好的效果。其中,本文算法在除t=71时的其他划分结果相较两层动态划分算法性能更好,体现了本文算法的有效性。由图7(b)可见,t=69~75时段内2个控制子区的饱和度逐渐减小,说明路网处于拥堵消散阶段。同时由图8可见,拥堵子区1(虚线区域)呈现先扩大后缩小的变化趋势。 图6 路网饱和度分布Fig.6 Saturation distribution of road network 图7 2分区下t=69~75时段算法划分性能Fig.7 Partition performance of algorithms att=69~75 under two partitions 图8 2分区下t=69~75时段控制子区演化过程Fig.8 Evolution process of control sub-regions att=69~75 under two partitions 本文结合密度峰值理论和狄利克雷问题求解模型,提出一种路网控制子区的动态划分算法,用以实现控制子区的快速寻优,同时提高子区边界的平滑性并捕捉控制子区的动态演化趋势。以美国法默布兰奇市的真实路网数据集作为案例进行分析,结果表明,该算法能够有效提升子区内部匀质性均值与归一化总方差,增强控制子区动态划分的时效性。下一步拟将该动态划分算法应用于边界控制中,并结合具体需求加以优化。

4 案例分析
4.1 数据集与θ值的敏感度分析


4.2 不同分区下静态划分效果分析


4.3 连续时段内动态划分效果分析


5 结束语
