受抑全内反射原理及应用

单曦辰,丁若禺,孙绪波,张文凯

(北京师范大学 物理学系,北京 100875)

全内反射(Total Internal Reflection),又称全反射,是指当光从折射率较高的介质入射到折射率较低的介质时,如果入射角大于临界角,则入射光会被完全反射回入射一方的介质. 但是在光疏介质界面一侧会存在一定强度的表面波,其振幅随入射深度的增加而呈指数衰减,这种表面波称为倏逝波(Evanescent Wave). 对于倏逝波的研究可以追溯到牛顿所在的时期[1]. 人们做了大量的实验来探究这一现象. 早在1897年,J. C. Bose通过实验证实了倏逝波的存在. 1902年,霍尔研究了在不同材料中倏逝波的隧穿深度与入射角、偏振方向的关系,在理论上计算了透射系数,从实验和理论上对倏逝波进行了解释[2]. 倏逝波的存在进一步导致了一个有趣的效应：受抑全内反射. 受抑全内反射(Frustrated Total Internal Reflection,FTIR)是指当光以大于临界角的角度入射到三层介质(光密-光疏-光密)时,光会在入射光一侧的光密介质和光疏介质的界面上发生全内反射;而随着两层光密介质之间的距离逐渐减小,直至第三层光密介质与光疏介质中存在的倏逝波发生相互作用,就会有部分光透射到第三层光密介质中去.

本文首先介绍了倏逝波和受抑全内反射,给出了受抑全内反射中透过率的理论公式. 利用MATLAB软件对影响透过率的因素进行了模拟,发现透过率与光疏介质宽度成负相关,且当光密与光疏介质折射率之比越接近1、入射角越接近全内反射临界角时,透过率越大. 此外,本文介绍了两种验证受抑全内反射的实验方案[3,4],有助于在学习或者教学中展示并深入理解受抑全内反射及其相关性质. 文章最后介绍了受抑全内反射在各个领域,比如材料、电子通信、传感器等方面的应用.

1 倏逝波

设入射面为xz平面,各物理量如图1所示.

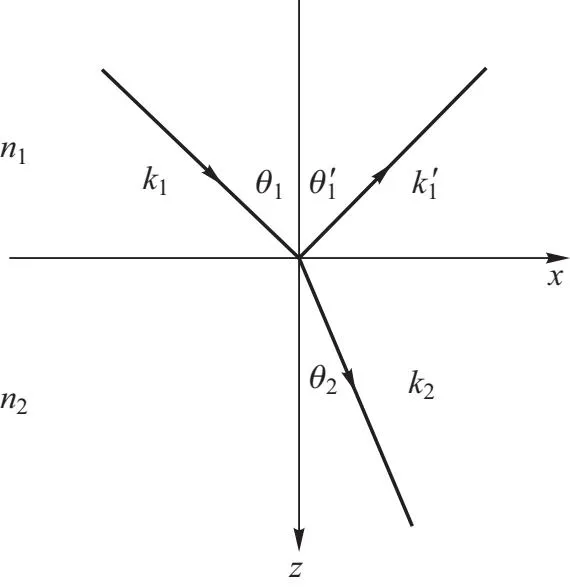
图1 光在不同介质界面上的折射

设入射电磁波电矢量为

Ei=E0eik1·r=E0ei(k1xx+k1zz)

(1)

折射电磁波电矢量为

Et=E″0eik2·r=E″0ei(k2xx+k2zz)

(2)

根据界面两端的波矢与折射率的关系和斯涅尔折射定律[5],当入射角θ1大于界面全内反射角θc时,即sinθ1>n2/n1,折射波的电矢量改写为

(3)

这是一个沿x正方向传播、振幅沿z方向指数衰减的横波,即倏逝波,如图2所示.

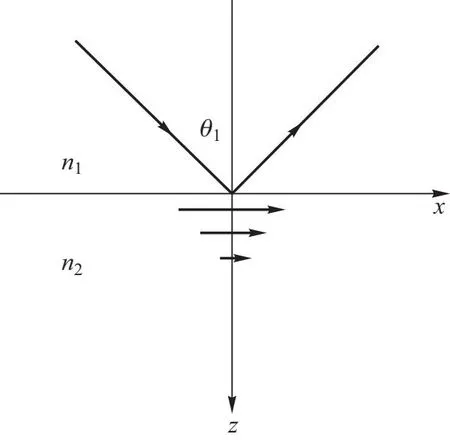
图2 全内反射时在光疏介质里产生倏逝波

2 受抑全内反射

与倏逝波相关的另一个重要的效应——受抑全内反射,则是因为当第三介质(通常折射率与入射方介质相等或接近)靠近时,倏逝波将会折射进入第三介质. 在宏观上看一部分光跳过缝隙直接进入了下一层介质,反射光并不包含入射光的全部能量,而是有一部分能量被透射到第三介质中去了.

图3 光在三层介质中的传播路径[6]

考虑这样一个结构：有三层均匀介质,折射率分别为n1、n2和n3,界面为平面且互相平行,间距为d,如图3所示. 一束光从介质1中入射,入射角为θ1,该入射角使得光在传播过程中不会在任何界面上发生全内反射. 结合斯托克斯公式,透射光电场强度为

Er=r12Ei+t12r23t21Eieiδ+…

(4)

(5)

(6)

其中

(7)

(8)

(9)

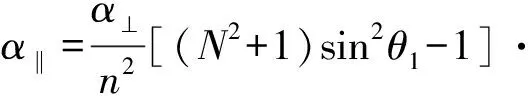
(10)

(11)

(12)

⊥表示电场垂直于入射面时的情况,‖表示电场平行于入射面时的情况.

图4 受抑全内反射示意图

为了简化运算,在这里采用相同的材料作为介质1和介质3,即n=n3/n1=1.

2.1 入射角θ1不变,光疏介质宽度d与透过率T的关系

对于大多数常见的实验材料,入射角θ1=70°便足以使得入射光在界面(1,2)发生全内反射. 取n1=1.5,n2分别等于1、1.2和1.33,以d/λ为纵坐标、透过率T为横坐标作图,得到的光疏介质宽度d与透过率T的关系如图5所示.

电场垂直于入射面时, T⊥与d的关系曲线

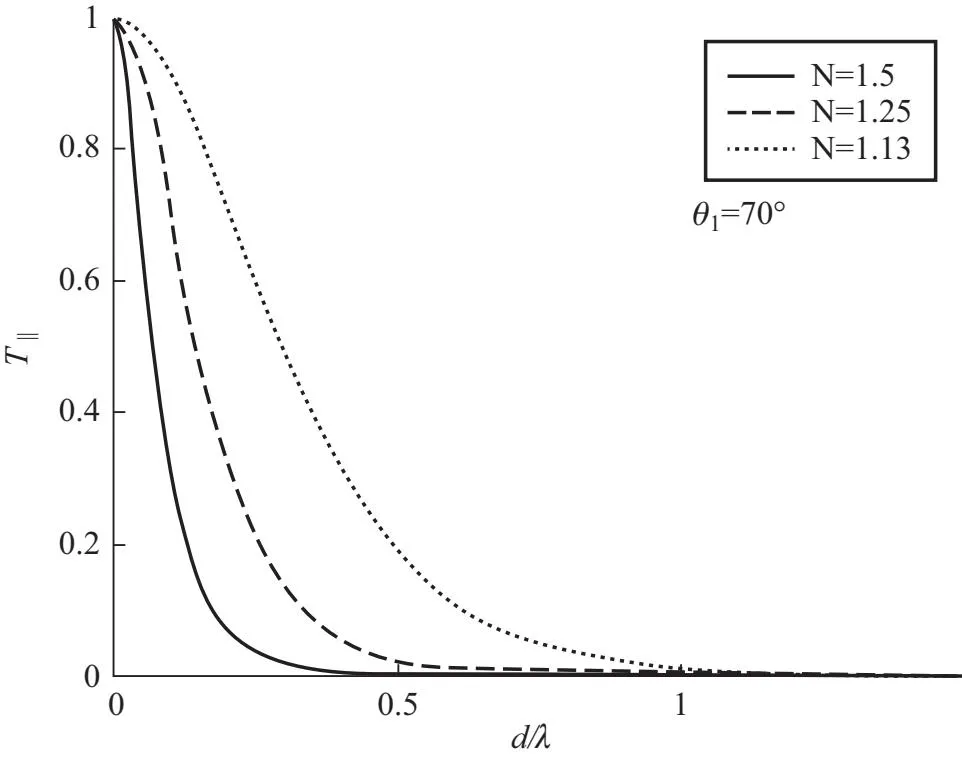
电场平行于入射面时,T‖与d的关系曲线图5 透过率T随光疏介质宽度d变化的关系曲线

2.2 光疏介质宽度d不变,入射角θ1与透过率T的关系

使光疏介质宽度d=0.5λ且保持不变,在不同的N的条件下使得入射角θ1从对应的全内反射角附近(略大于全内反射角)开始增大,得到的透过率T与入射角θ1的关系如图6所示.

电场垂直于入射面时,T⊥与θ1 的关系曲线

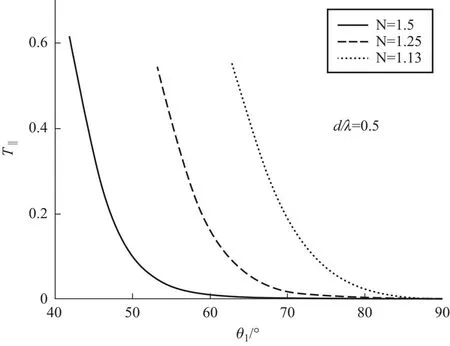
电场平行于入射面时, T‖与θ1 的关系曲线图6 透过率T随入射角θ1变化的关系曲线

可见,当入射角λ和光疏介质宽度d一定时,N越小,也即介质1和介质2的材料折射率n1和n2越相近时,透过率T越大. 于是,如果想要在实验中观察到更明显的受抑全内反射,需要使得：(1)d尽可能地小;(2) 入射角θ1尽可能地接近全内反射角;(3) 介质1和介质2的材料折射率尽可能地接近.

3 验证实验

Z.Vörös和R. Johnsen[3]用两块三棱镜夹住一片很薄的铝箔,使两个三棱镜中形成了一道空气隙,如图7所示. 空气隙的宽度随入射点的移动而线性变化,由此可以通过测量入射点位置a计算得到光疏介质宽度d,并结合测得的透射光强度,从而绘制出T-d关系曲线. 和理论结果图5对比,如果符合,即可验证受抑全内反射.

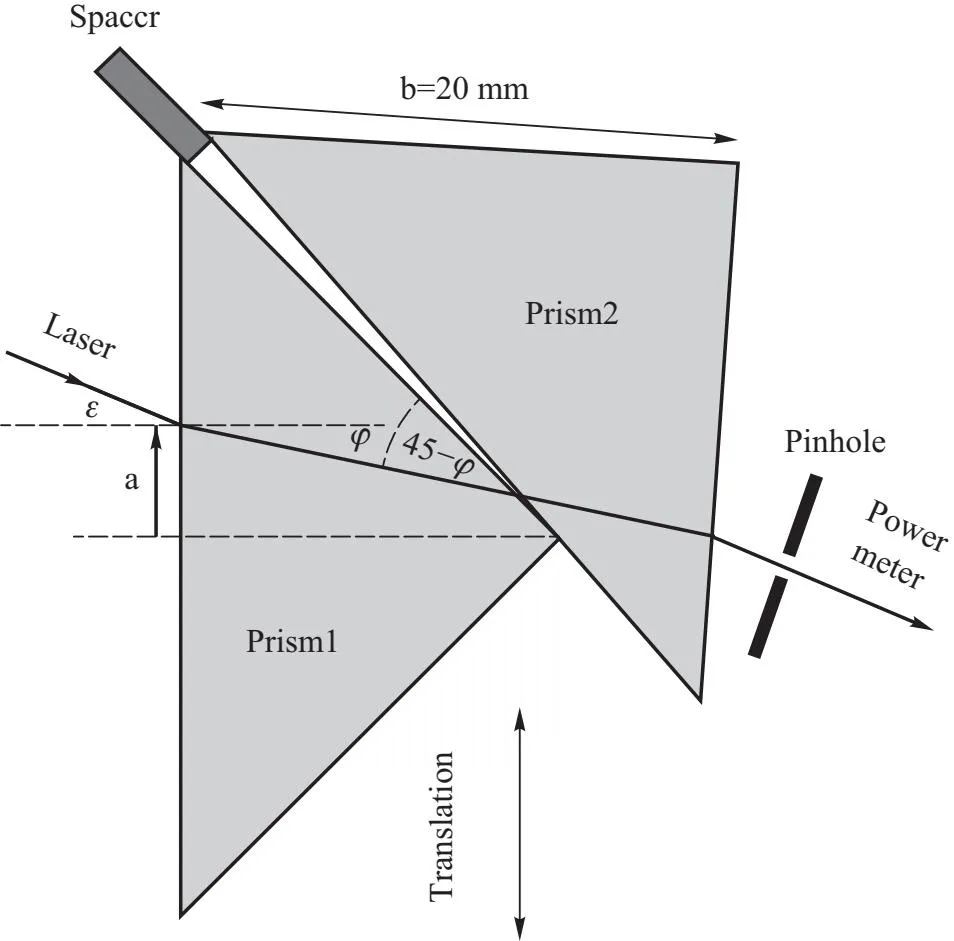
图7 利用双棱镜系统验证光隧穿效应的实验装置示意图[3]

DA.Papathanassoglou和B. Vohnsen则设计了一种更直观的验证实验方案[4]. 他们同样利用了三棱镜,使入射光在三棱镜的一个光学面上发生全内反射,然后用一根很细的探针逐渐由远及近地靠近入射点. 探针被作为第三介质与倏逝波发生作用,也可以诱发受抑全内反射. 用相机记录下探针距离光学面不同距离时的透射光,如图8所示.

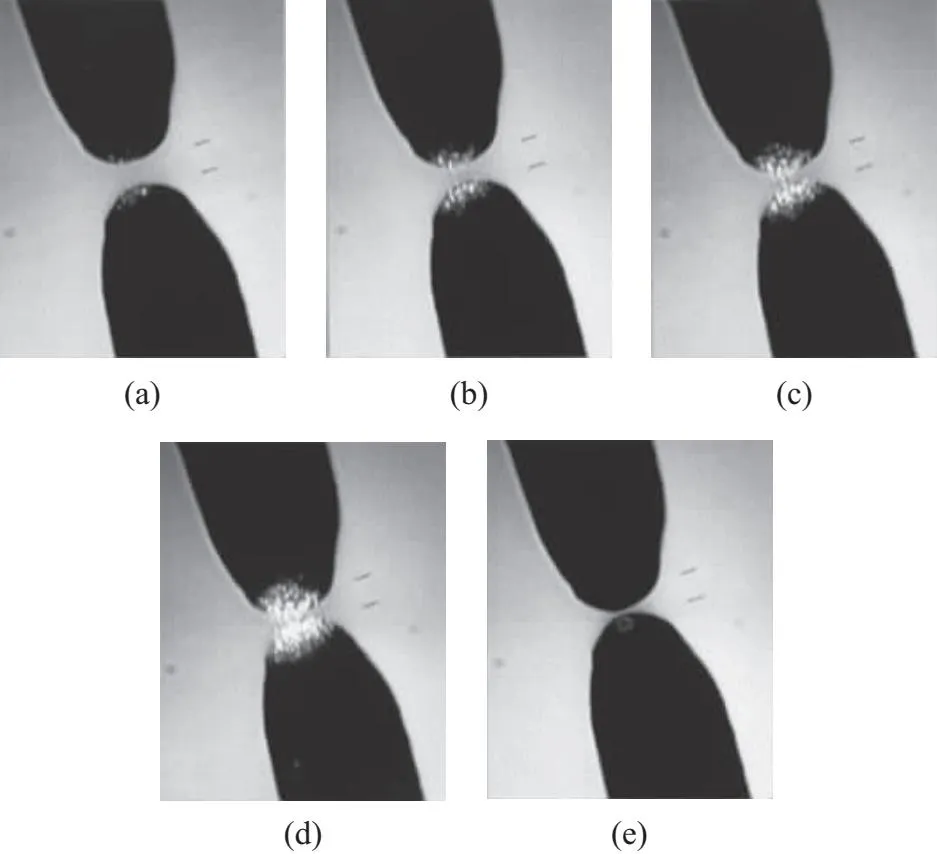
图8 利用探针诱发受抑全内反射的实验相片[4]. 其中白色的部分即为透射光;每张照片中下方阴影是探针,上方的阴影是探针被三棱镜光学面反射后成的像. 图a～d对应探针逐渐靠近反射点的情形;图e是关闭光源时的参照相片.

4 应用

4.1 光子扫描隧道显微镜

光子扫描隧道显微镜的原理是当一束光在棱镜介面上发生全内反射时,在倏逝波波长量级之内的情况下,如果把一个折射率大于棱镜外介质的光纤探针接近样品,就会产生受抑全内反射,场强与光纤探针离棱镜表面的距离呈指数衰减关系. 如果在棱镜表面放上样品,则倏逝场受到样品表面形貌的调制. 所以当扫描样品表面时,样品表面起伏就通过场强表达出来了. 光子扫描隧道显微镜可应用于原子操纵光学近场测量[8]、Al2O3波导薄膜检测[9]等领域.

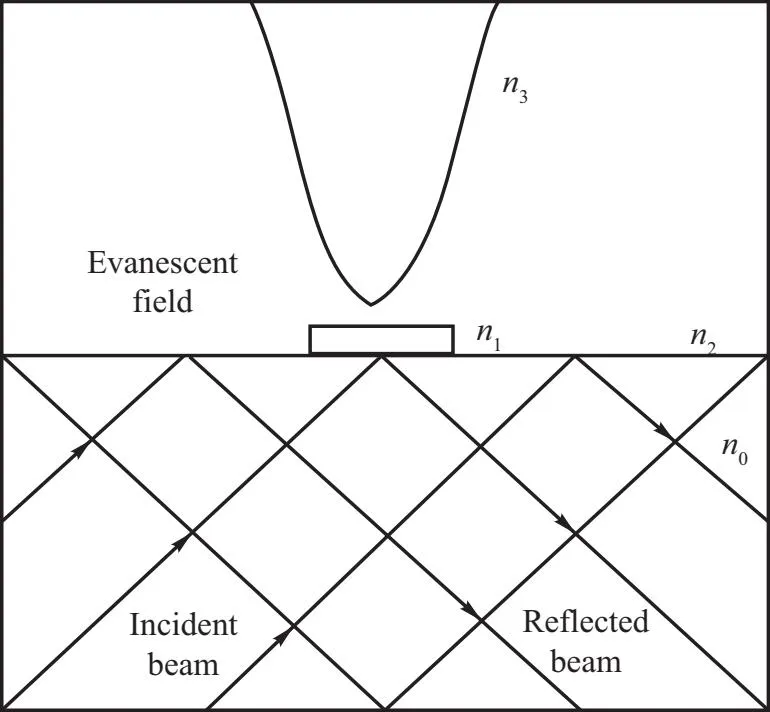
图9 光子扫描隧道显微镜的原理图[10]

4.2 光耦合器

受抑全内反射可用于作为集成光学中的光耦合器,而且可以用棱镜耦合器将激光耦合进入波导薄膜. 只需要将一个高折射率的棱镜放置在波导薄膜之上,并且控制棱镜和波导薄膜之间的缝隙以形成一个很薄的空气层,之后调整入射光在下表面的入射角大于棱镜-空气界面的全内反射临界角,通过受抑全内反射入射光就会被耦合进光波导中,这种把光耦合进入波导的器件就是输入耦合器. 根据光路的可逆性,同理可以得到输出耦合器,耦合效率的理论值最高可达100%. 光耦合器已经被广泛应用于多个方面如电动汽车快速充电桩[11]、信息光学实验[12]、开关电源的故障监测[13]等.

4.3 力传感器

压力场传感是一项复杂的测量任务. 利用受抑全内反射的原理来测量施加到表面上的压力的方法已经被科学界广泛应用于多项测量任务[14]. 基于受抑全内反射的力传感器的原理是：当相比于玻片更为粗糙的物体表面挤压玻片时,由于二者之间的距离与可见光波长数量级相当,在间隙发生受抑全内反射,因此能透过薄玻片看到粗糙物体的表面由于凹凸不平而显现的亮区,从而利用光的受抑全内反射现象,可以将接触压力的大小转换成光强信号,即可以利用相机或光敏传感器测量压力的大小[15]. 通过算法与简化模型进行分析,则可得到数值结果. 这种方法被广泛利用,尤其是足底压力测试[16]以及轮胎压力测试[17]系统.

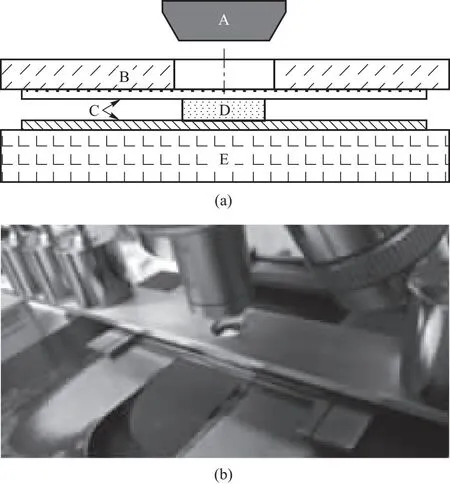
图10 显微力学观察光学实验台：A：显微镜透镜、B：铝框、C：显微镜载玻片、D：聚合物薄片试样、E：载玻片架台[17]