手性回音壁微腔的有限元仿真

2024-01-12张维元俞骁翀

大学物理 2023年12期

张维元,俞骁翀

(北京师范大学物理学系,北京 100875)

光学微腔能够同时在空间和频率维度上约束光场,将谐振光子长时间局限在微纳尺度,并多次作用于模式范围内的物质,极大增强了光与物质相互作用,是基础光物理和光子学应用研究的重要平台[1].其中,基于全内反射约束光场的回音壁微腔具有超高的品质因子和很小的模式体积,备受研究者们关注,在微型激光器[2-5]、微腔非线性光学与光频梳[6-7]、集成光子学回路[8-9]和高灵敏光学传感[10-15]等领域得到广泛应用.

光学微腔中的回音壁模式满足矢量波动方程以及电磁场边界条件.除了二维圆腔、三维球腔等少数旋转对称规则几何形状具有简单的解析解外,人们也发展了多种近似手段和数值方法分析介观微腔中的回音壁模式.一般回音壁模式按偏振可以分为横电(TE)模式和横磁(TM)模式,在结构对场约束不太大时大致为线偏振状态,这也限制了回音壁模式与一些手性物质的相互作用时的可区分度.

本文考虑在微腔中使用手性材料,以得到相比常规回音壁模式更为丰富的模式偏振,开拓回音壁模式的偏振调控自由度,可以更好的进行各种基础光物理和光子学应用.基于麦克斯韦方程组和手性材料唯象本构关系,本文将对存在手性材料时的回音壁模式偏振特性进行分析,建立并验证适用于有限元方法的手性材料微纳结构仿真框架.

1 手性材料中的电磁场

对于旋光性相对较弱的常见手性材料,将唯象本构关系中的与旋光性相关的交叉耦合项作为微扰,已经足以计算出光学模式以及对应的本征频率.但是考虑到日益发展的纳米技术,电磁场之间的交叉耦合越来越不适合作为微扰效应,开发非微扰的模式求解手段还是非常有必要的.

首先考虑本构关系[16-18]：

(1)

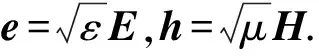
(2)

(3)

在均匀材料区域中,e±ih分别满足矢量亥姆霍兹方程：

(4)

独立边界条件可以取：

(5)

由于电磁场在均匀介质中满足横波条件,上述矢量亥姆霍兹方程解的形式只能取为

e±ih=

(6)

其中,A±可以取为标量亥姆霍兹方程的解乘以一个简单矢量场.可以发现,在手性材料存在下,电磁场不可能由单一的线偏振场来描述.以下以波动方程的平面波解和柱面波解为例,简要分析手性材料中的电磁场传播模式和谐振模式特性.

1.1 平面电磁波

对于平面电磁波,可以取

(7)

直接得到

电磁场为左右旋圆偏振平面波的叠加.由于两束圆偏振光具有不同的波速,偏振方向将发生旋转,即产生旋光现象.

1.2 柱面电磁波

对于轴对称结构,考虑半径为R的二维圆腔,其内外相对介电常数和磁导率分别为ε、μ和ε1、μ1.利用对称性,内外部分别取为

(9)

其中k和k1分别为腔内外的波矢,z方向为轴向,其内部和外部解分别为

(10)

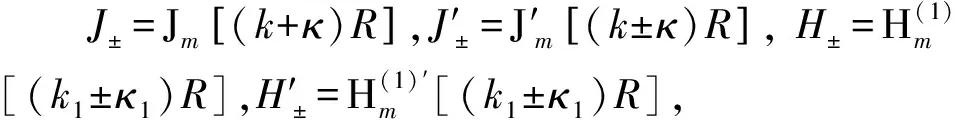
(11)

对于常规材料(κ1= 0),上式变为常见的二维圆腔特征方程

(12)

其中J+=J-=J,H+=H-=H.特征方程左侧两项分别代表不同的偏振模式.

2 手性材料微结构的有限元电磁场仿真

对于其它更加不规则的结构,上述理论分析可以通过模式分解、边界元等手段进行数值计算,但是需要针对不同的应用情形进行开发.而有限元等仿真方法则直接通过数值求解麦克斯韦方程组得到电磁场分布,更具有通用性.以下将通过改写具有唯象本构关系麦克斯韦方程组,实现通用的、兼容主流有限元软件的手性材料仿真框架.使得计算手性材料存在下的传播、散射、耦合、本征值问题更加方便.

2.1 有限元仿真框架

通过重新定义电位移和磁场强度矢量

(13)

可以将存在手性材料的麦克斯韦方程组变换为自洽的有源形式

(14)

其中,自由电荷密度

ρe=-i

(15)

电流密度

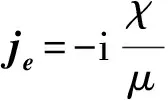
(16)

在材料交界面处,还将存在由χ突变所引起的边界电流

(17)

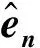
(18)

至此,需要求解的变量均只与电场相关,兼容常规的波动光学仿真的设置.

2.2 二维圆腔仿真

利用COMSOL软件的波动光学模块,在二维轴对称模型下,对圆腔进行了仿真.圆腔半径R=10 μm,内外部折射率分别为1.445和1,方位角模式数m=50,内外部手性b=b1同步变化.仿真结果如图1所示.其中,本征频率在手性反号时不发生变化(图1a).这可以从两方面进行解释：从对称性角度,手性反号等价于进行了一次镜像操作,模式也变为其镜像;从特征方程角度,等价于公式(11)中的正负脚标发生交换,并不改变特征方程.这说明镜像对称的常规微腔仅通过简单观察模式的谐振频率移动来进行手性物质的区分是不可行的.而当模式存在对称破缺时,如果微腔存在垂直于旋转轴的反映面,也无法从本征频率区分手性的符号.将仿真得到的模式场分布与直接求解波动方程得到的精确解进行了比较(图1b-d),发现两者完全重合,证明上述仿真方法的可靠性.

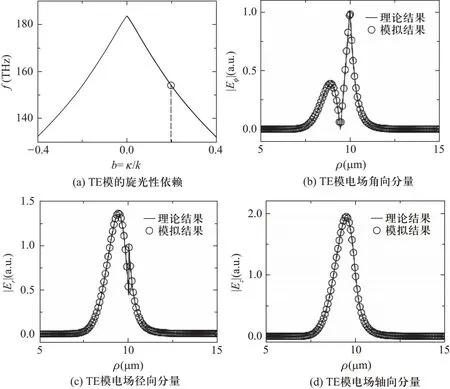
图1 圆腔模式的场分布及旋光性依赖.

引入手性材料后,腔模偏振特性如图2所示.定义手性参数P=(|Er+iEz|2-|Er-iEz|2)/2(|Er|2+|Ez|2)来表征模式中左右旋圆偏振光的比例,结果显示了与旋光参数间的强烈依赖.在初始无旋光的情形下,腔内模式为线偏振的TE模和TM模.当腔体材料具有旋光性时,腔内的电场逐渐由线偏振变为椭圆偏振,并最终成圆偏振.其中原TM模式的偏振波动较大是因为与其他模式交叉耦合所致,使它具备了一些周围模式的偏振特性.

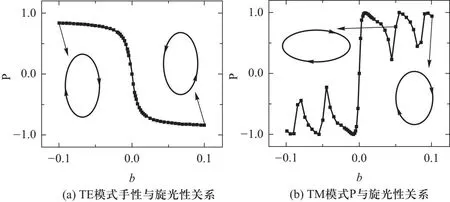
图2 (a) 微腔边界处TE模式的手性随旋光参数的变化,插图为b=-0.1和0.1时的电场偏振态(b) 微腔边界处TM模式的手性随旋光参数的变化,插图为b=0.05和0.1时的电场偏振态

当微腔内外材料的手性不再同步变化时,内部或者外部手性变化才有可能导致不对称的模式移动.图3比较了内部手性从零变到非零(b=0.2)时,腔模谐振频率对外部介质手性的响应,以及外部手性从零变到非零(b1=0.2)时,腔模谐振频率对内部介质手性的响应.当内部或外部介质具有旋光性时,腔模谐振频率确实产生了非对称的手性响应.这使得我们有望通过检测模式的谐振频率来测量介质的旋光性,并进而对其成分进行确定.特别地,初始的TE和TM模式的响应是相反的,这更加有助于提高灵敏度并补偿环境扰动.

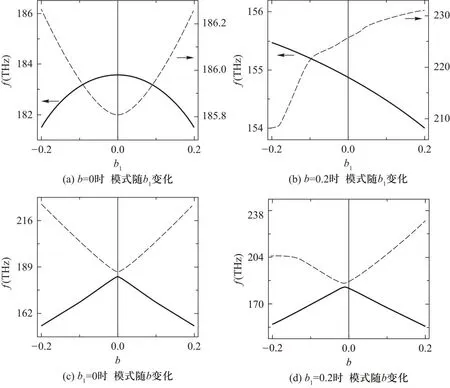
图3 在内外部材料手性不同步变化时,TM和TE模式与旋光性的依赖关系,其中虚线为TM模式,实线为TE模式.

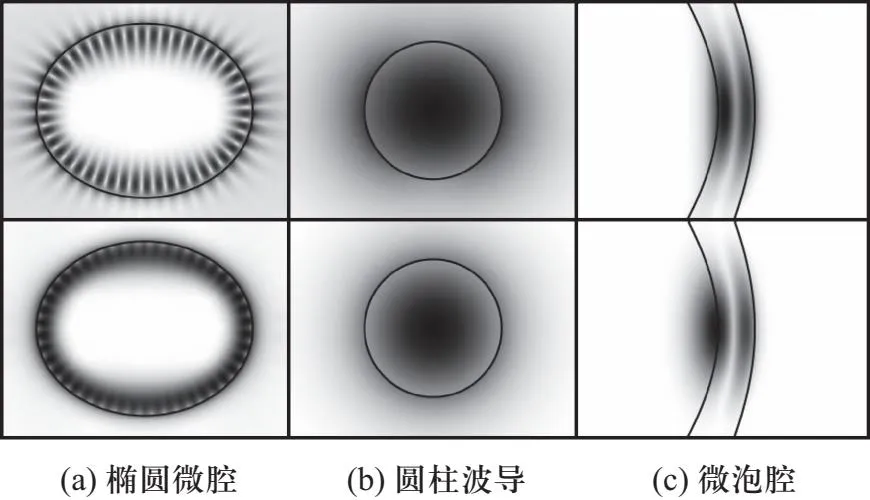
图4 三类常见微结构中手性诱导的模式分布变化,上图为无旋光性,下图为有旋光性.

2.3 对其它旋光性微纳结构的仿真

对于其他手性材料微纳结构,前述的有限元仿真框架均能够进行有效的计算.在图4中,展示了由手性材料组成的椭圆微腔(图4(a))、圆柱波导(图4(b))以及内部存在手性溶液的三维微泡腔(图4(c))的模式电场分布(下图),并与无手性的常规微纳结构(上图)进行了对比,可以明显发现手性材料对模式偏振的影响.例如在手性圆柱波导中,基模的场分布是旋转对称的,明显表现出了圆偏振模式的特征.