非对称人工超导结构中的涡旋动力学分析与模拟
2024-01-12戴晴琴
戴晴琴
(北京师范大学 物理学系,北京 100875)
对于第Ⅱ类超导体,当外加磁场大小介于上下临界场之间时,其正常态(N)与超导态(S)的界面能为负值,从而允许外磁场以磁通涡旋(vortex)的形式穿入超导体内部,形成超导与正常态涡旋共存的混合态(mixed state, MS)[1]. 此时如果在垂直于磁场的方向外加电流,则单根磁通在单位长度上会受到洛伦兹力f=Φ0J,从而发生运动[2].
非理想超导体中总是会存在一些缺陷,例如晶界、点或面缺陷、杂质相等. 为降低整个体系的自由能,涡旋会倾向于被钉扎在这些位置[1]. 这一类能够阻碍涡旋运动的区域被称为钉扎中心,其与涡旋的相互作用被称为钉扎力.
近年来,利用不对称钉扎控制涡旋动力学过程的研究引起了人们极大的兴趣,常被用于设计磁通泵、整流器或二极管等[3-7]. 涡旋的相互作用及其动力学行为决定了超导体几乎所有的电、磁学特性,通过对涡旋的动力学研究,可以深入了解超导材料的物性和超导机制,为其工业化应用提供理论支撑.
本文基于此目的开展研究,首先对涡旋运动基本模型进行简单介绍,后加入对涡涡相互作用力的考虑,利用MATLAB软件进行数值模拟比较涡旋数目、洛伦兹力大小、交流电周期对涡旋运动的影响,最后加入热噪声扰动项,从而实现了对超导体中涡旋动力学过程的简单模拟.
1 涡旋运动基础模型[8]
1.1 不对称周期势
考虑如图1所示几何形状的II型超导体薄膜,其钉扎势分布满足U(x,y)=U(x)=U(x+l)即在y方向具有平移不变性,而在x方向呈现以l为周期的变化,包括l1上升沿与l2下降沿. 周期中最大势能为ΔU.由于假定l1大l2,且钉扎势[8]满足
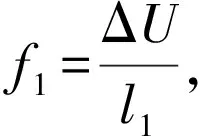
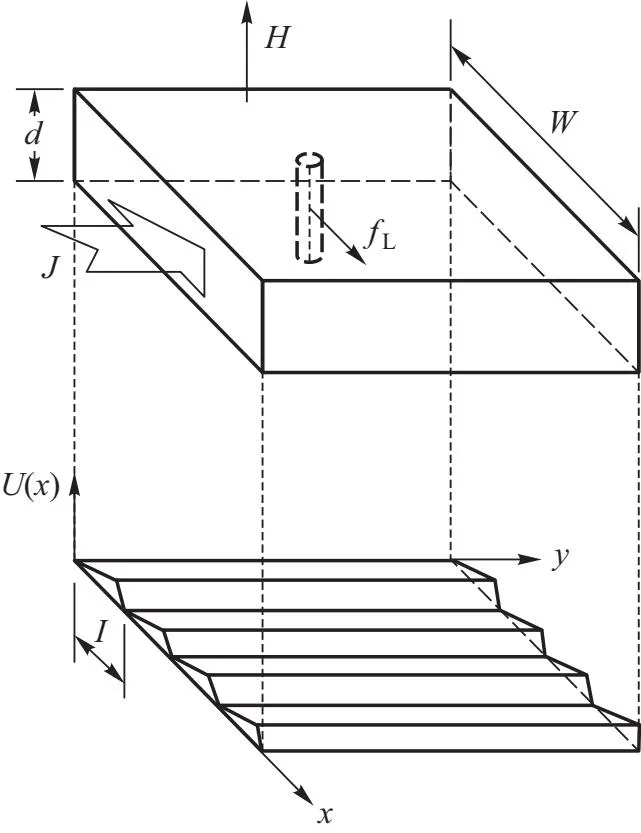
图1 具有不对称势的超导体示意图
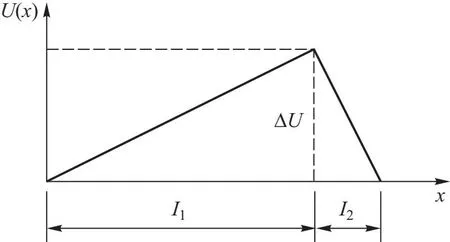
图2 不对称势参数(x方向)
1.2 洛伦兹力
如图1所示,给样品施加y方向交流电,涡旋将受到洛伦兹力[8]:
(2)
1.3 运动方程与解析解
考虑上述两种受力,涡旋满足动力学方程[8]
ηv=fL+fu
(3)
其中η为黏度,fL为洛伦兹力,fu为钉扎力,v为某时刻受力后产生瞬时速度.
当直流电沿正y方向流动时,洛伦兹力使涡流沿正x方向以速度v+移动;改变电流方向后,涡旋速度反向,记作v-.由于势的不对称,v+与v-大小并不相等,从而产生沿某一方向的净速度[8]:
根据f1、f2与洛伦兹力fL的相对大小,考虑交流电周期趋于无穷大,可分为3种运动情况.
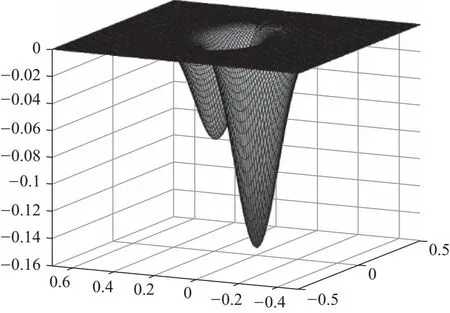
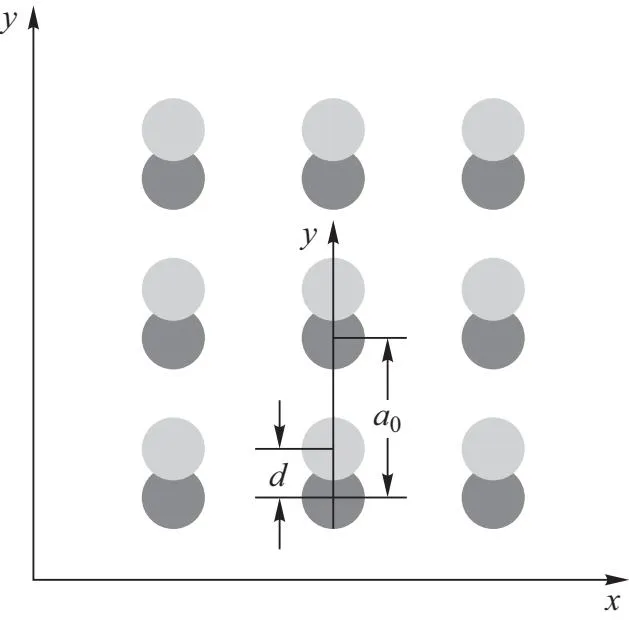
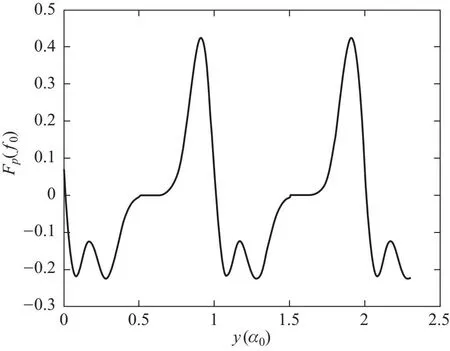
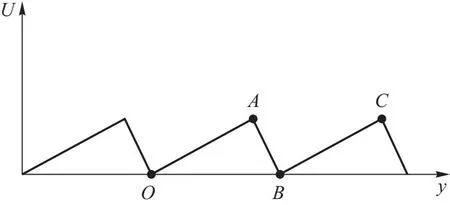
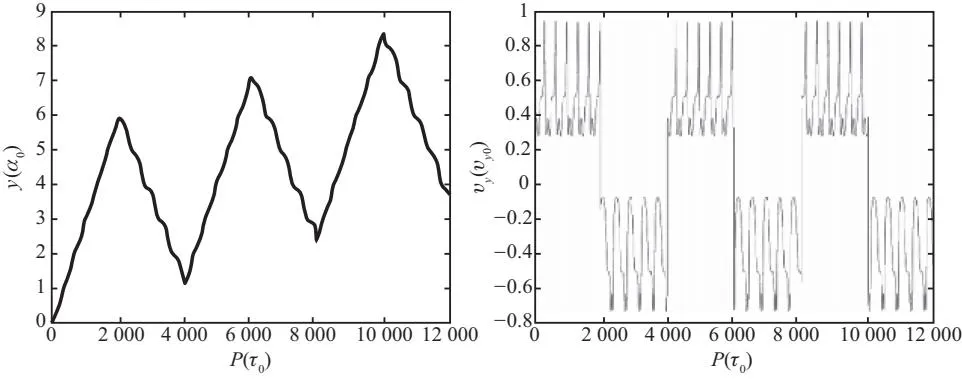
当fL v1=0 (5) 当f1 (6) 同时v2-=0,故有[8]: (7) 当f2 (8) 其净速度[8]为 (9) 利用MATLAB对以上速度解进行绘图.值得注意的是,本文重点研究各力、速度、位移之间的相对大小,对于绝对值不作严格讨论,故全文中所绘图像均以a0为位移单位,f0为力常数单位,v0为速度单位,vy0为y方向分速度单位. 在实际计算以及生产运用中,只需要将各单位代入具体数值计算即可. 图3 v随fL的变化关系 涡旋速度在fL=f2时达到最大值,若洛伦兹力继续增大,则会出现过驱动现象,即速度随洛伦兹力增大而减小. 如图4所示,通过在样品上设置部分重叠的强弱钉扎位点,模拟产生不对称周期势. 图4 单组强弱钉扎示意图 钉扎中心采用衰减长度为Rp高斯势阱模型,则单个钉扎的钉扎力[9]可表示为 (10) 其中fp0为钉扎力常数,ri为涡旋位置,R为钉扎中心所在位置,强弱钉扎的不同之处体现在力常数与钉扎位置上. 如图5所示,在二维样品的x与y方向等间距a0设置一系列强弱钉扎,各组强弱钉扎间距离为d. 图5 样品中强弱钉扎位置示意图 固定x的值,利用MATLAB模拟y方向各位点所受钉扎力fp的受力情况如图6所示. 图6 钉扎力随y方向变化情况 当样品中的涡旋个数大于1时,涡旋不光会受到钉扎力与洛伦兹力,涡旋之间的排斥相互作用也应当考虑在内. 可假设该力大小与两涡旋间距离成反比,方向指向两涡旋连线方向即[9] (12) 其中ri为第i个涡旋的位移,rj为第j个涡旋的位移,fvv0为涡涡相互作用力常数,并设置截止作用距离为5a0. 加入对涡涡相互作用的考虑后,涡旋动力学方程修正为[9] ηvi=fL+fvv(ri)+fp(ri) (14) 利用生成随机数的方法获得涡旋的初始位移,设置迭代步长τ0,利用牛顿法的思想进行迭代. 首先利用初始位置求得受力,得到初始速度,再利用 x←x+vτ0 (15) 获得更新后的位置,重复上述操作,并绘制一个涡旋相应的时间-y方向位移曲线与时间-y方向速度曲线. 涡旋运动情况与洛伦兹力的大小、周期密切相关. 如图7所示,控制洛伦兹力大小不变,且f1 图7 单涡旋y方向位移(左)/速度(右)- 时间曲线 运动结果可借助图8进行分析解释,设初始时刻涡旋位置为O,洛伦兹力沿y轴正方向. 图8 涡旋位置示意图 当周期较小为400τ0时,涡旋首先沿y轴正方向运动,爬升至OA段中间时,洛伦兹力反向,又回到初始位置. 当周期增大至500τ0时,涡旋可沿正方向从O点运动至BC段,后洛伦兹力反向,涡旋会到B点,对应图中的沿y轴负方向位移,但由于f1 当周期继续增大至700τ0时,涡旋可运动至BC段偏C处段,故对应的位移后退会更加明显,且仍然存在平台期. 增大洛伦兹力使得f1 图9 增大洛伦兹力后的涡旋运动曲线 该模拟结果对应模型中的过驱动情况,即正负方向均有速度,但由于v+>|v-|,故仍存在y方向的净位移. 为进一步探究在固定洛伦兹力下,涡旋运动速度随周期的变化情况,可引入一涡旋平均速度Vdc,其定义为各涡旋在一个时间周期内的速度平均即[9] (18) 控制其他参数不变,且维持f1 图10 涡旋的速度-周期曲线 为更好模拟涡旋运动的真实情况,对热噪声的考虑是不可避免的,可看作许多比涡旋更轻的粒子对其碰撞产生了热噪声力[10],运动方程因此变为[9] ηvi=fL+fvv(ri)+fp(ri)+fT(t) (21) 利用拆分法[11](Splitting method)对上述朗之万方程进行模拟,将原方程拆分为ABO三项. B项: v←v+F/2 (22) 其中F为除热噪声外的合力,处理思路与2.3节类似,通过(12)式来计算某处受力产生的速度. A项: x←x+vτ0/2 (23) 由于此处使用拆分法,故更新位置时仅计算半个迭代步长对应的位移. 而关于噪声项有 (24) 由Ornstein-Uhlenbeck过程表示噪声扰动项,其中α为均值回归速率,回归均值设为0,β为波动率,dW表示遵从高斯分布的布朗运动. 解该方程即可得到O项: (24) 其中R为均值为0,方差为1的高斯随机数. 完成上述BAOA过程对应一个完整的迭代周期,将加入热噪声的单个涡旋周期-速度曲线与为考虑热噪声时的图像对比,如图11所示. 图11 单涡旋加入噪声前(左)后(右)的速度-周期曲线 当噪声较小时,图像趋势不变,仅光滑程度受到影响. 本文首先对涡旋在超导体中的受力进行了简单分析,包括由不对称周期势产生的钉扎力、随时间周期性变化的洛伦兹力,并由此列出涡旋的运动学方程. 进一步就各力的相对大小关系进行了讨论,可分为三种情况:当洛伦兹力小于钉扎力时,涡旋被困在钉扎中心无法运动;当洛伦兹力大于某一方向的钉扎力时,涡旋可受洛伦兹力驱动克服钉扎力进行单方向运动;当洛伦兹力大于两个方向的钉扎力时,涡旋将处于过驱动状态,向具有净速度的一方移动.由此求得了涡旋运动方程的解析解,并用MATLAB完成图像绘制,发现在洛伦兹力大小与较大钉扎力相等时取得涡旋运动的最大速度. 其次在上述模型的基础上,加入对涡旋间相互作用力的考虑,利用MATLAB进行数值模拟,绘制了涡旋运动的位置-时间图以及速度-时间图,并探究了洛伦兹力大小与交流电周期对其产生的影响,结合基础模型对其分析解释. 进一步地,绘制了不同涡数所对应的平均速度-交流电周期图,在T→∞与解析解相对应. 最后用Ornstein-Uhlenbeck过程表示噪声扰动项,利用Splitting method对朗之万方程进行数值模拟,绘制了噪声扰动下的速度-周期曲线,并与未考虑噪声时的曲线进行对比. 电流驱动涡流的动力学研究对于理解强相互作用涡流的基本集体行为以及在超导体中获得高非耗散电流具有重要意义[12],且在许多应用中发挥着关键作用,例如高场磁体[13]、超导数字存储器和量子位[14]、太赫兹辐射源[15]或用于粒子加速器的谐振腔[16]等.本文基于前人研究,对超导体中涡旋运动进行了简单分析与模拟,并在模型中加入对热噪声干扰项的考虑,使其更贴近真实应用情境,具有一定的现实意义. 致谢: 感谢北京师范大学刘海文教授对本文提出的修改意见。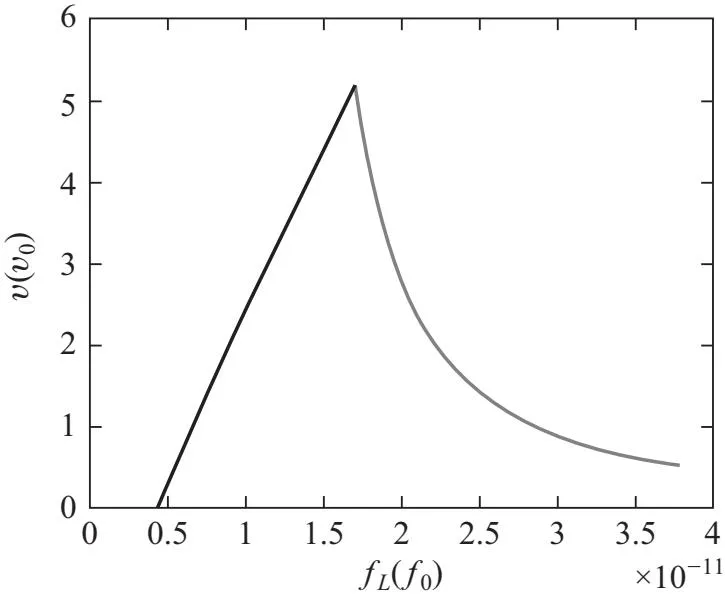
2 涡旋运动数值模拟
2.1 不对称周期势模拟
2.2 涡涡相互作用模拟
2.3 数值模拟方法
2.4 单个涡旋模拟结果
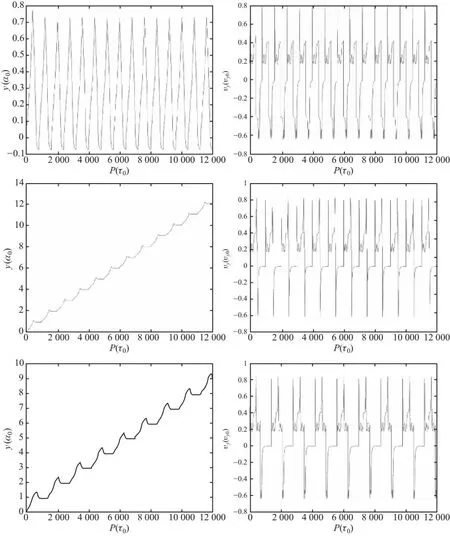
2.5 涡旋的速度-周期曲线
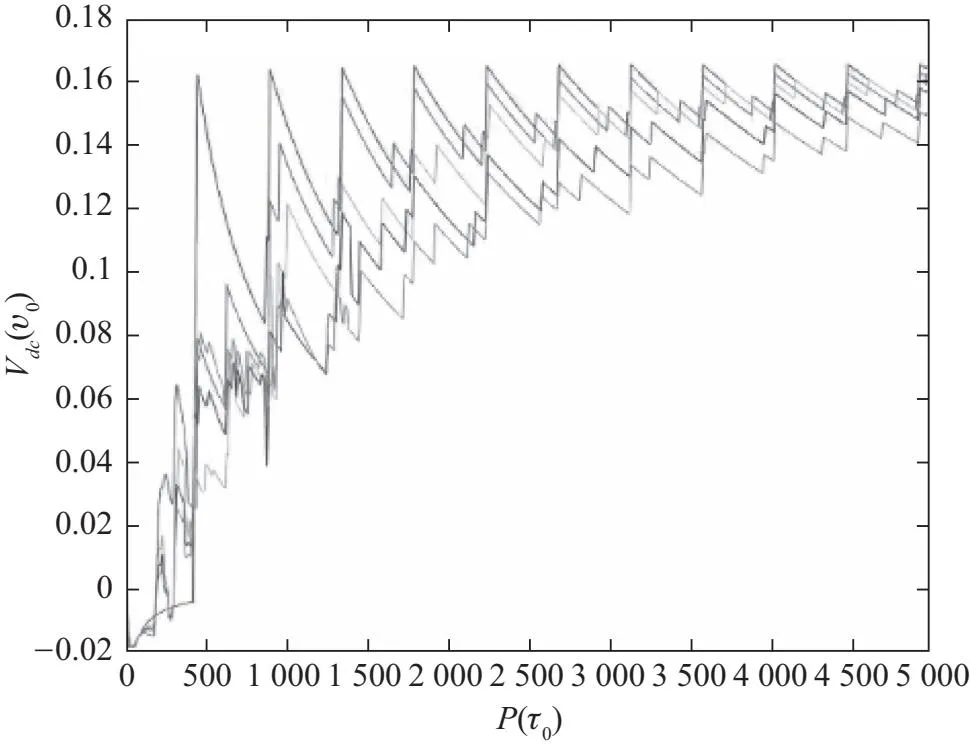
3 热噪声下的涡旋运动
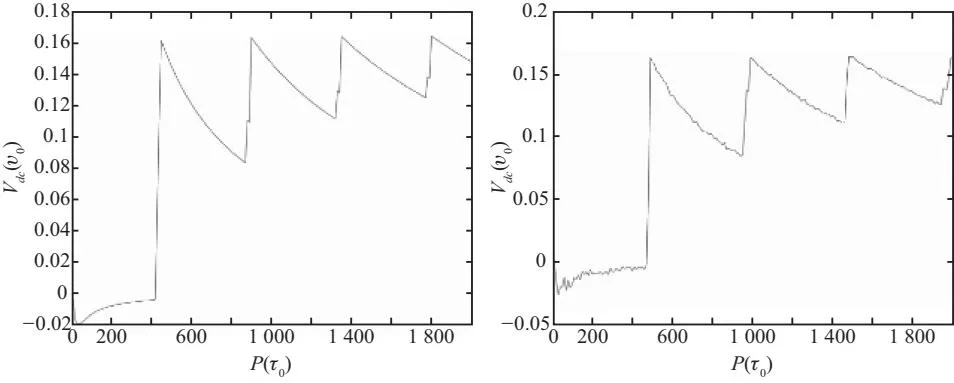
4 结论
