对一道几何光学竞赛题解结果的分析

邱会明

(南京市金陵中学,江苏南京 210005)

1 一道几何光学竞赛题及原解答

原题.两块平面镜宽度均为 L=5 cm,相交成角α=12°,如图 1 所示,构成 光通道.两镜的右端相距为 d=2 cm,左端靠在光接收器的圆柱形的感光面上.试问入射光线与光通道的轴成的最大角度 φmax为多少才能射到光接收器上?[1]

图1

原参考解答:不经反射,入射光能射到感光面上,入射光与轴所成最大角 φ1如图2所示;经一次反射而能入射在感光面上,入射光与轴所成最大角φ2如图3所示,由平面镜反射的对称性,入射光延长能交在2α所对圆面上,同理可推出,以最大角度 φmax入射的光线延长后应恰与接收器表面相切,如图4所示,θ为入射光线与平面镜所成的夹角,φmax=其中≈0.5,θ≈30°,则φmax=30°+6°=36°.

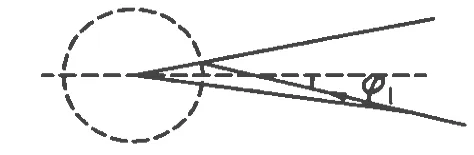
图2

图3

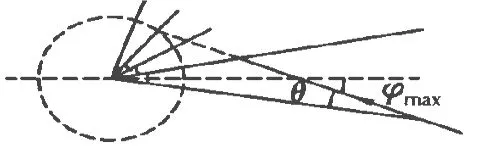
图4

2 对题解结果的重新计算及作图分析

2.1 对结果的重新计算

笔者通过计算发现,在取一位有效数字的精度范围内,θ的取值应为 28.5°,28.5°能约等于 30°吗?

2.2 用几何画板作图分析

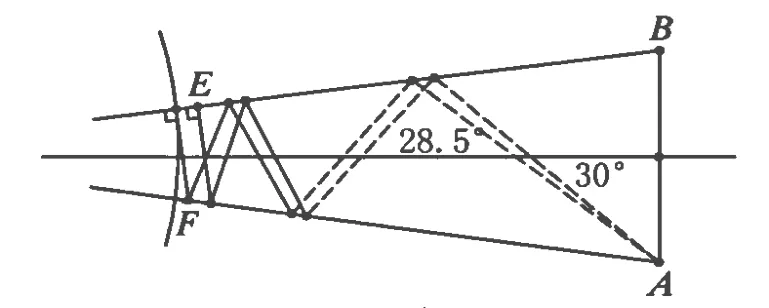
图5

由此可见,在作图误差允许的范围内,θ应该取28.5°来计算,φmax应为 34.5°.

图6

3 对原解答的重新审视

3.1 一个有趣的结论及推广

我们把经过平面镜多次反射的光线都延长就可以发现一个有趣的结论:只要开始的入射光线与感光圆面是相切的,那么经过平面镜多次反射的光线的延长线都会与感光圆面相切.这是为什么呢?其实这是与圆的对称性有关.如图6所示,第1次反射过程中,入射光线与反射光线关于OB对称,因此反射光线的延长线与圆也是相切的;第2次反射过程中,反射光线的延长线与入射光线关于 OA对称并与圆相切;依次可以推出,以后的多次反射过程中,入射光线、反射光线的延长线分别关于OA、OB对称且始终与圆相切,最后的反射光线与感光圆面相切.

同理可以得出如下的结论:只要开始入射光线与圆是相交的,那么经过平面镜多次反射的光线的延长线都会与感光圆面相交.

3.2 对原解答的重新审视

图4中开始的入射光线的延长线与感光圆面是相切的,依据前面的结论可以得到,光经过平面镜的多次反射,最终的反射光线与感光圆面相切.图2、3中,虽然开始的入射光与轴所成的角最大,但其入射光线与圆是相交的,依据前面推广结论可以得到,最后的反射光线与感光圆面相交.由此可见,原解答中把小数约去后变成一个整数竟为我们发现问题提供了一个突破口,其逻辑推理是完全错误的.从上面的分析可以看出,只有在理解上述结论之后,才能得出φmax等于34.5°的正确结论.

1 沈晨.更高更妙的物理.杭州:浙江大学出版社,2006.